基于漂角观测的无人帆船反步自适应控制

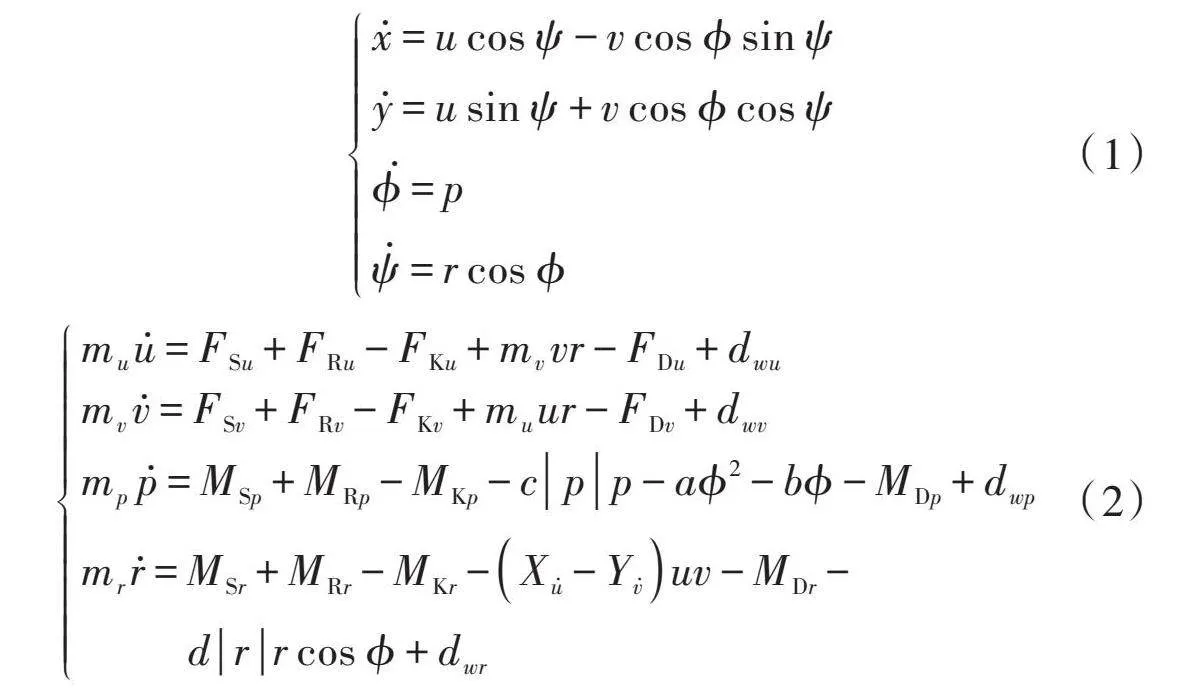
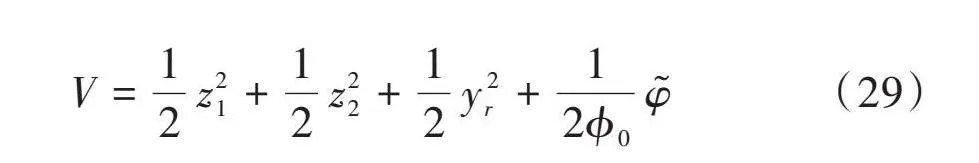
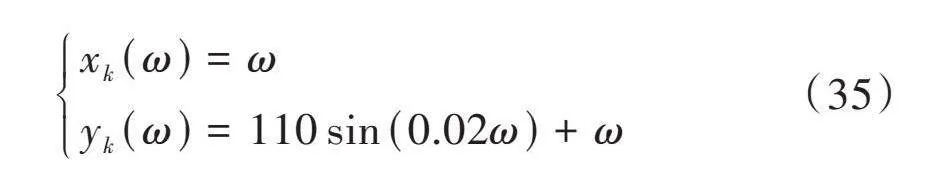
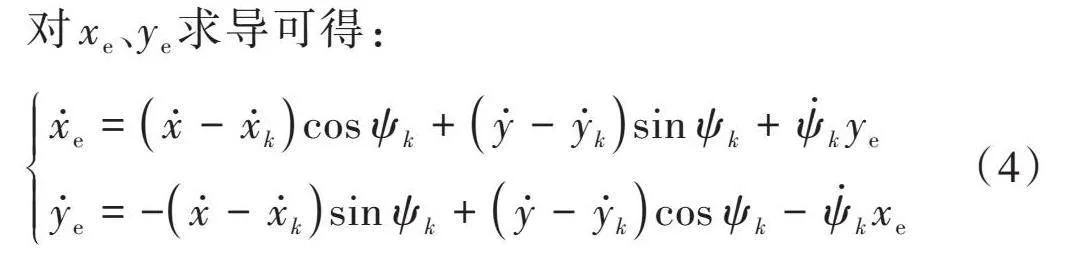
摘" 要： 针对无人帆船路径跟踪控制问题，提出基于双有限时间漂角观测器的视线法制导和反步自适应控制方案。双有限时间漂角观测器对时变漂角进行了精确观测，观测误差有限时间收敛，提高了视线法制导的鲁棒性和精度。对于航向追踪，采用反步法设计控制器，动态面滤波器来解决虚拟控制律的微分爆破问题，自适应更新律补偿无人帆船的外部扰动。通过仿真实验表明，有限时间观测器提高了对漂角的观测精度，并且基于双有限时间漂角观测的视线法具有更加精确的路径跟踪效果，反步自适应控制器具有良好的控制效果。

关键词： 漂角； 有限时间观测； 无人帆船； 路径跟随； 自适应控制； 反步法

中图分类号： TN609⁃34； TP273" " " " " " " " " " " 文献标识码： A" " " " " " " " " "文章编号： 1004⁃373X（2025）03⁃0129⁃06

Unmanned sailboat′s backstepping adaptive control based on sideslip angle observation

SHAO Kangjian， LIU Daofa

（Taihu Laboratory of Deepsea Technological Science Lian Yun Gang Center， Lianyungang 222000， China）

Abstract： In allusion to the path following and control of unmanned sailboat， a line⁃of⁃sight guidance and backstepping adaptive control scheme based on double finite⁃time sideslip observers is proposed. The time⁃varying sideslip angle is observed accurately by double finite⁃time sideslip observers， and the observation error converges in finite time， which improves the robustness and accuracy of the line⁃of⁃sight guidance. For heading tracking， the backstepping method is adopted to design the controller， the dynamic surface filter is used to cope with the differential explosion of the virtual control law， and the adaptive update law is used to compensate the external disturbance of the unmanned sailboat. The simulation results show that the finite⁃time observers improve the observation accuracy of the sideslip angle， and the line⁃of⁃sight method based on double finite⁃time sideslip observers has a more accurate effect of path following， and the backstepping adaptive controller has a great effect of control.

Keywords： sideslip angle; finite⁃time observation; unmanned sailboat; path following; adaptive control; backstepping

0" 引" 言

无人帆船属于欠驱动船舶，它相对于普通船舶来说具有耗能少、航行时间长等优点，因此其在海洋及大型湖泊的环境监测上具有很大优势[1]。由于无人帆船在执行任务中需要有规定的路线，所以其路径跟随控制需要有高精度及强鲁棒性，其路径跟随控制由制导和航向控制组成，制导是指根据路径的变化给出一个参考角度，参考角度的准确性直接关系到路径跟踪的精度，航向控制则是追踪制导角。

近年来，对于无人帆船的研究很多集中在控制器上。文献[2]设计反馈线性化控制器模拟了帆船在港口内巡航控制。文献[3]研究了帆船转向时的动力学模型，为减小计算过程设计PI控制器。文献[4]和文献[5]通过反步法设计控制器实现了航向控制，该控制器设计较简单，没有考虑到扰动未知影响。文献[6]将水手的操帆、操舵经验转化成Mamdani型模糊推理系统。文献[7]根据船员航海操舵经验设计245条模糊控制规则进行航向调整，但是模糊控制不够精确，因此需要考虑对所受扰动进行处理且易调参的控制方法。

视线制导广泛应用于欠驱动船舶的制导，如文献[8]考虑传统视线法易受环境影响，提出适合直线路径跟踪的积分视线法（ILOS）。除此之外，许多方法通过观测侧滑角来提高视线制导角的准确性，例如，文献[9]提出具有自适应侧滑角观测的视线法制导（ALOS），由于进行了小角度假设，漂角的估计变得不准确，从而使视线法制导精度降低，而且漂角剧烈变化时，漂角估计效果变差。文献[10]提出了基于扩展状态观测器的视线法制导（ELOS），可以精确观测快速时变侧滑角，并通过实验验证了有效性。文献[11]开发了复合LOS（CLOS），基于时延控制方法和降阶线性扩展状态观测器（LESO）技术，侧滑角的精确观测对于欠驱动船舶的航迹跟踪非常重要。文献[12]提出了基于双扩展状态观测器的视线法制导（DELOS），但对于帆船来说，侧滑角度的精确观测研究还是缺乏的。

为此，本文提出一种基于漂角观测补偿和反步自适应的无人帆船路径跟踪控制方法。设计了双有限时间漂角观测器对无人帆船航行时的漂角进行精准观测，提高制导系统的鲁棒性，并基于反步动态面技术设计控制器、自适应律来补偿外界扰动未知问题。仿真结果表明，漂角观测提升了制导角的精确性，并且反步自适应控制器具有良好的跟踪效果。

1" 基础知识

基于参考文献[4]，可以得到四自由度无人帆船运动学模型和动力学模型为：

[x=ucos ψ-vcos ϕsin ψy=usin ψ+vcos ϕcos ψϕ=pψ=rcos ϕ] （1）

[muu=FSu+FRu-FKu+mvvr-FDu+dwumvv=FSv+FRv-FKv+muur-FDv+dwvmpp=MSp+MRp-MKp-cpp-aϕ2-bϕ-MDp+dwpmrr=MSr+MRr-MKr-Xu-Yvuv-MDr-drrcos ϕ+dwr] （2）

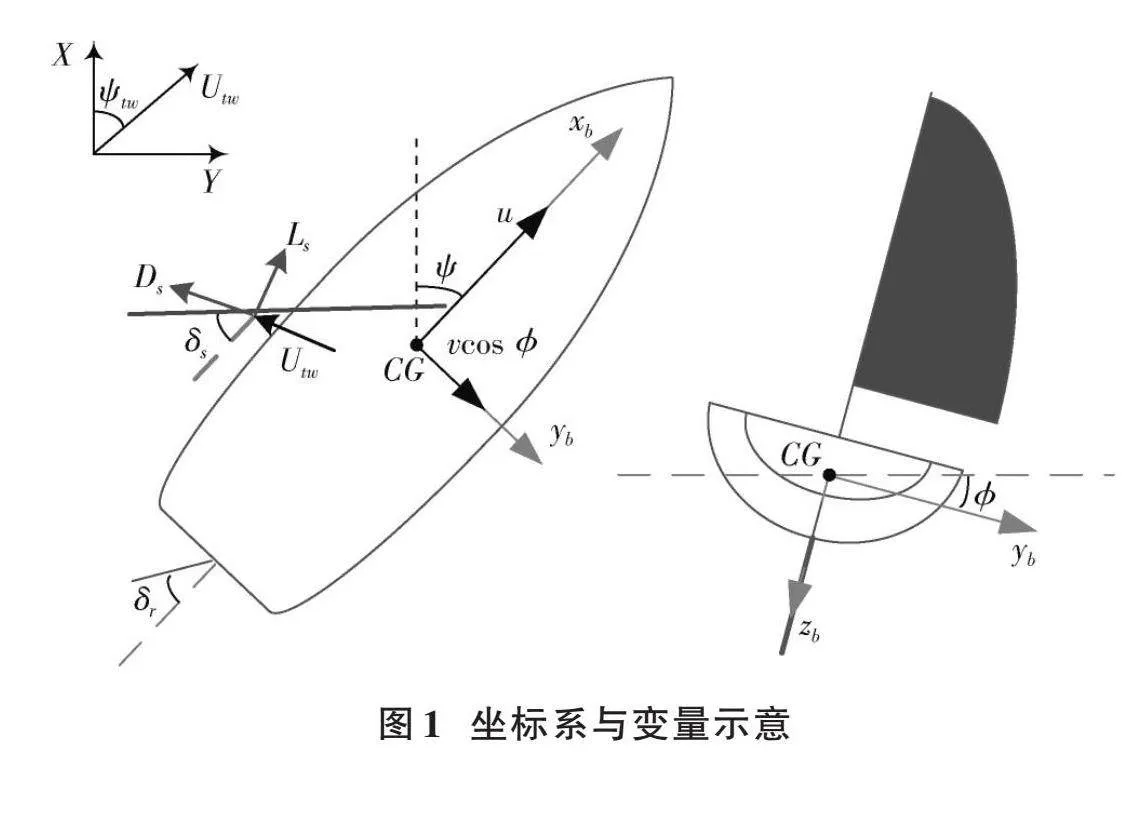
式中：[mu=m-Xu]；[mv=m-Yv]；[mp=Ixx-Kp]；[mr=Izz-Nr]；[Fij][ （i=R，S，K，D，j=u，v，p，r）]分别表示帆船的舵（R）、帆（S）、龙骨（K）和船体（D）产生的力；[Mij][（i=R，S，K，D， j=u，v，p，r）]分别表示帆船的舵（R）、帆（S）、龙骨（K）和船体（D）产生的力矩；[dwi（i=u，v，p，r）]为各自由度风浪干扰力之和。如图1所示，向量[η=[x，y，ϕ，ψ]T]，[（x，y）]代表无人帆船在惯性坐标系下的位置，[ϕ]代表无人帆船横摇角，[ψ]代表无人帆船艏摇角；向量[ν=[u，v，p，r]T]，[u]代表无人帆船的纵向速度，[v]代表横向速度，[p]代表横摇角速度，[r]代表艏摇角速度。

根据人工操帆经验，采取如表1所示的控帆方法。

2" 基于漂角观测的视线法制导

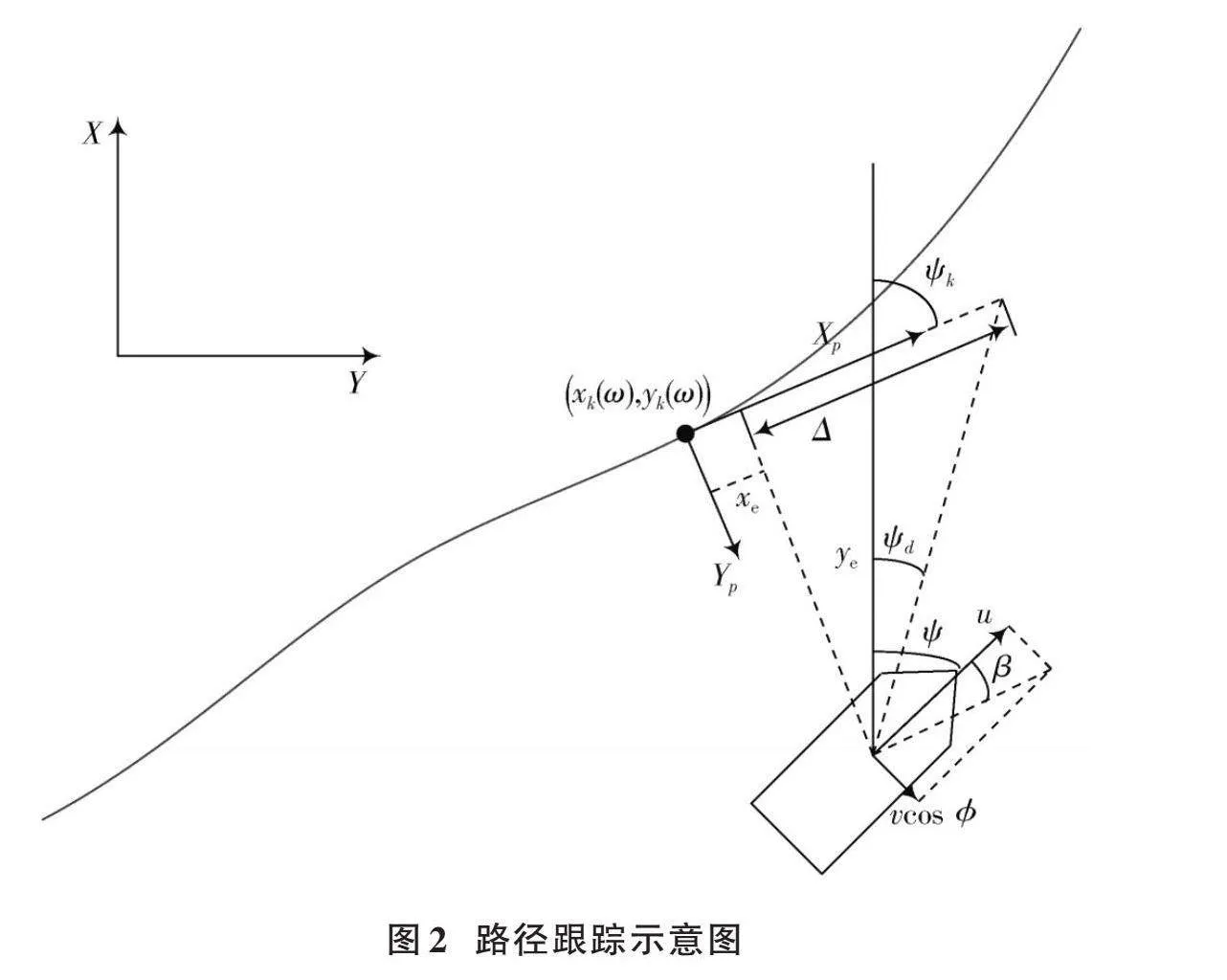
如图2所示，建立参数化参考路径及船舶在水平面的投影具有的位置和姿态关系，[ω]表示路径参数变量，路径的形状由含有[ω]的函数表示，参考路径的坐标点用[xk（ω），yk（ω）]表示，路径的正切角表示为[ψk=arctany'kx'k]，其中[y'k=∂yk∂ω]，[x'k=∂xk∂ω]。无人帆船的位置[x，y]与参数化路径上虚拟目标点[（xk（ω），yk（ω））]的误差在参考坐标系下的表达形式如下：

[xeye=cos ψksin ψk-sin ψkcos ψk·x-xk（ω）y-yk（ω）] （3）

对[xe]、[ye]求导可得：

[xe=x-xkcos ψk+y-yksin ψk+ψkyeye=-x-xksin ψk+y-ykcos ψk-ψkxe] （4）

将式（3）代入式（4），可推导出：

[xe=Ucosψ-ψk+β+ψkye-upye=Usinψ-ψk+β-ψkxe] （5）

式中：[U=u2+（vcos ϕ）2]为无人帆船的合速度；[β=arctanvcos ϕu]为漂角；[up]为虚拟目标点沿参考路径的移动速度，[up=ωx'k2+y'k2]。考虑误差[xe]收敛，设计虚拟速度[up]为：

[up=Ucosψ-ψk+β+kxxe] （6）

式中[kx]是正的调节参数。

[ω]的更新律如式（7）所示：

[ω=Ucosψ-ψr+β+kxxex′r2+y′r2] （7）

在实际的航行中，无人帆船的漂角是未知的，能否精确地观测漂角对于视线法制导来说十分重要。为此，根据文献[13]设计双有限时间漂角观测器对未知漂角进行精确观测，漂角观测误差可以在有限时间内收敛到零，其具体设计如式（8）、式（9）所示：

[xe=-λ1sig45xe+h1+ψkye-uph1=-λ2sig35xe+ϑ1sgnxe] （8）

[ye=-λ3sig45ye+h2-ψkxeh2=-λ4sig35ye+ϑ2sgnye] （9）

式中：[h1=Ucosψ-ψk+β]；[h2=Usinψ-ψk+β]；[xe]、[h1]分别是[xe]、[h1]的估计值；[ye]、[h2]是[ye]和[h2]的估计值；[λi（i=1，2，3，4）]、[ϑj（j=1，2）]均为正的调节参数。有误差[xe=xe-xe]，[h1=h1-h1]，[ye=ye-ye]，[h2=h2-h2]，对其求导，则有：

[xe=-λ1sig45xe+h1h1=-λ2sig35xe] （10）

[ye=-λ3sig45ye+h2h2=-λ4sig35ye] （11）

因此，根据文献[13]的证明可知：[xe]、[h1]、[ye]、[h2]是有限时间收敛到零，即存在时间[0lt;Tβlt;∞]，使得[xe≡xe]，[h1≡h1]，[ye=ye]，[h2=h2]；[ϑ1][sgnxe]、[ϑ2][sgnye]的加入是为了提升系统的鲁棒性。

漂角可以用[h1]、[h2]表示为：

[β=arcsinh2cosψ-ψk-h1sinψ-ψkU] （12）

漂角的观测误差为：

[β=arcsinh2cosψ-ψk-h1sinψ-ψkU] （13）

故可知漂角观测误差在有限时间内收敛到零。

在非逆风下视线法跟踪角表示为：

[ψdp=ψk-arctanyeΔ-β] （14）

针对上述公式，误差公式化简为如下形式：

[xe=-kxxe+ψkyeye=-Uyey2e+Δ2cos（β+ψ）-UΔy2e+Δ2sin（β+ψ）-ψkxe] （15）

选取Lyapunov候选函数为：

[V2=12x2e+12y2e] （16）

式（16）两边对时间求导得：

[V2=xexe+yeye=-kxx2e+ψkyexe-Uy2ey2e+Δ2cos（β+ψ）-UΔyey2e+Δ2sin（β+ψ）-ψkxeye≤-kxx2e+2Umaxye+Δ=-kxx2e-kxy2e+2Umaxye+Δ+kxy2e=-kxV2+2Umaxye+Δ+kxy2e] （17）

式中：[Umax]是[U]的最大值；令[Δe=2Umaxye+Δ+kxy2e]，则有[V2=-kxV2+Δe]，因此路径跟随误差是全局渐进稳定的。

3" 反步自适应控制器

由于控制器设计部分只考虑航向运动，则根据式（1）和式（2）可以得到如下无人帆船航向运动数学模型：

[ ψ=rcos ϕmrr=MSr+MRr-MKr-Xu-Yvuv-MDr-drrcos ϕ+dwr] （18）

考虑航向控制器设计，现提出如下两个假设。

假设1：考虑到航行实际，船舶所受到风浪载荷是有界的，则可以假设无人帆船所受的外界扰动有界且变化率有界。

假设 2：无人帆船的制导角是光滑可导有界的，并且其一阶导数与二阶导数也是有界的。

定义航向跟踪误差如下：

[z1=ψ-ψd] （19）

根据航向跟踪误差[z1]以及航向期望角导数[ψd]设计虚拟控制律如下：

[αr=1cos ϕ（-k1z1+ψd）] （20）

式中[k1]为正的调节控制参数。

为避免直接对虚拟控制律求导产生“微分爆炸”问题，引入动态面技术，通过[θ]对[αr]进行估计，其表达式为：

[τrθ+θ=αrθ（0）=αr（0）] （21）

式中[τr]为滤波时间常数。

定义闭环系统动态面滤波中[αr]的跟踪误差为：

[yr=θ-αr] （22）

通过[θ]代替[αr]避免计算复杂问题，令式（22）对时间求导可得：

[yr=θ-αr=-yrτr+∂αr∂ψψ+∂αr∂ψdψd+∂αr∂ψdψd+∂αr∂ϕϕ=-yrτr+B] （23）

式中[B]是一个连续函数且有上界[M]，其中[M]是一个正常数。

定义帆船艏摇角速度误差变量[z2]如下：

[z2=r-θ] （24）

由于外界扰动是未知的，为补偿外界风浪扰动影响，设计如下自适应更新律：

[φ=ϕ0z222λ2-ϕ1φ] （25）

自适应参数估计误差为[φ=φ-φ]。

设计无人帆船舵角控制律如下：

[αM=-MSr+MKr+Xu-Yvuv+MDr+drrcos ϕ+（θ-c2z2）mr-φz22λ2] （26）

[δ'r=arcsin2αM-1.2ρARv2arxr] （27）

考虑执行器舵角的实际转动限制，对舵角进行限幅：

[δr=δ'r，" " "δ'rlt;π6π6sgn（δ'r），" " "δ'r≥π6] （28）

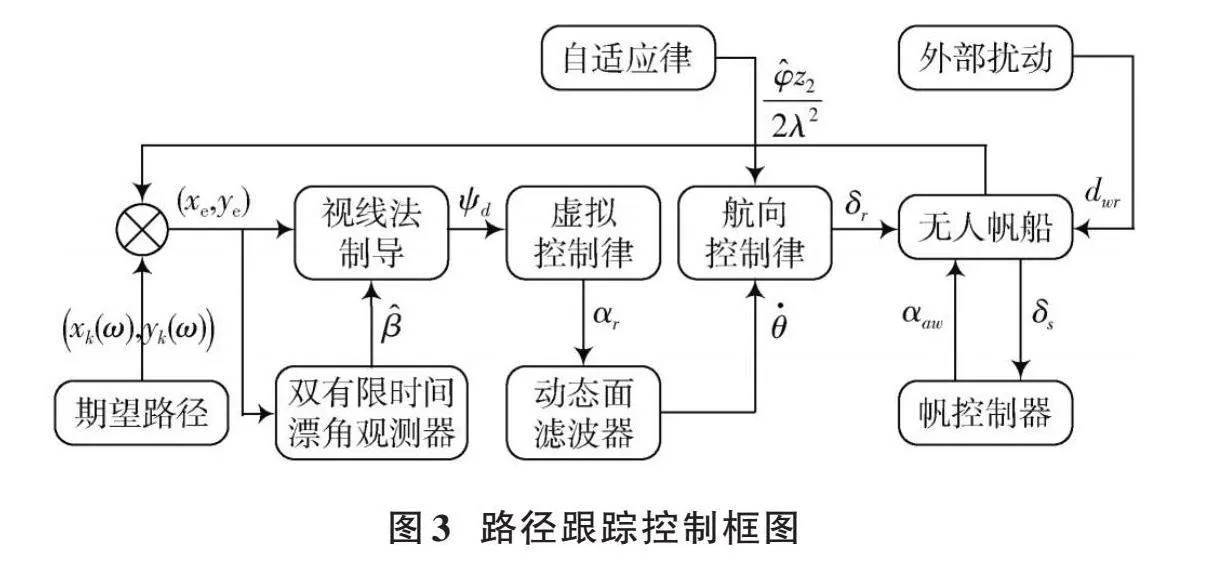
因此本文控制框图如图3所示。

采用Lyapunov进行证明，选取Lyapunov候选函数为：

[V=12z21+12z22+12y2r+12ϕ0φ] （29）

Lyapunov函数对时间求导得：

[V=z1z1+z2z2+yryr+φφ=z1[（z2+yr+αr）-ψd]+z2（r-θ）+yr-yrτr+B+φφ] （30）

将式（20）、式（25）和式（27）代入式（30）得：

[V≤z1z2cos ϕ+z1yrcos ϕ-c1z21-c2z22-y2rτr+yrB-ϕ1φφ] （31）

结合帆船航行实际情况，可得横倾角的范围是[-π2]～[π2]，因此有如下不等式成立：

[V≤z1z2+z1yr-c1z21-c2z22-y2rτr+yrB-ϕ1φ22+ϕ1φ22] （32）

进一步化简式（32）可得：

[V≤12（z21+z22）+12（z21+y2）-c1z21-c2z22-y2rτr+12y2rB2+12-ϕ1φ22+ϕ1φ22=-（c1-1）z21-c2-12z22-1τr-M22y2r-ϕ1φ22+12+ϕ1φ22] （33）

因此可以得到：

[V≤-aV+c] （34）

式中，[a]和[c]需满足：

[a=min（c1-1），c2-12，1τ-M22，ϕ12]

[c=ϕ1φ22+12]

因此通过对控制参数的调节可以得到当时间趋于无穷大时，航向闭环控制系统的所有信号是一致最终有界的。

4" 仿真实验

为验证本文提出的制导与控制方法的有效性，基于文献[4]的12 m无人帆船模型进行仿真验证，该船长12 m、宽3.21 m，船的质量为25 900 kg，其他详细参数参考文献[4]。

为保证仿真效果的真实有效性，参考文献[14]建立真实的风浪干扰，风向为正南风，设定风速为5 m/s，则波浪有义波高为0.7 m，通过与文献[12]的DELOS和文献[8]的ILOS进行对比实验来验证基于双有限时间漂角观测器的视线法制导的优越性。在仿真中文献[8]的方法命名为No.1，文献[12]的方法命名为No.2，本文方法命名为No.3。设计无人帆船期望轨迹如下：

[xk（ω）=ωyk（ω）=110sin（0.02ω）+ω] （35）

在仿真模拟中无人帆船的初始位置是[-25，0] m，初始的纵向速度为1 m/s，其余状态的初值均设为零。控制参数设置为：[kx=0.1]，[λ1=20]，[λ2=100]，[λ3=20]，[λ4=100]，[ϑ1=0.001]，[ϑ2=0.001]，[Δ=30]，[k1=10]，[τ=0.1]，[k0=6]，[c2=2]，[ϕ0=2]，[ϕ1=0.01]，[λ=0.5]。

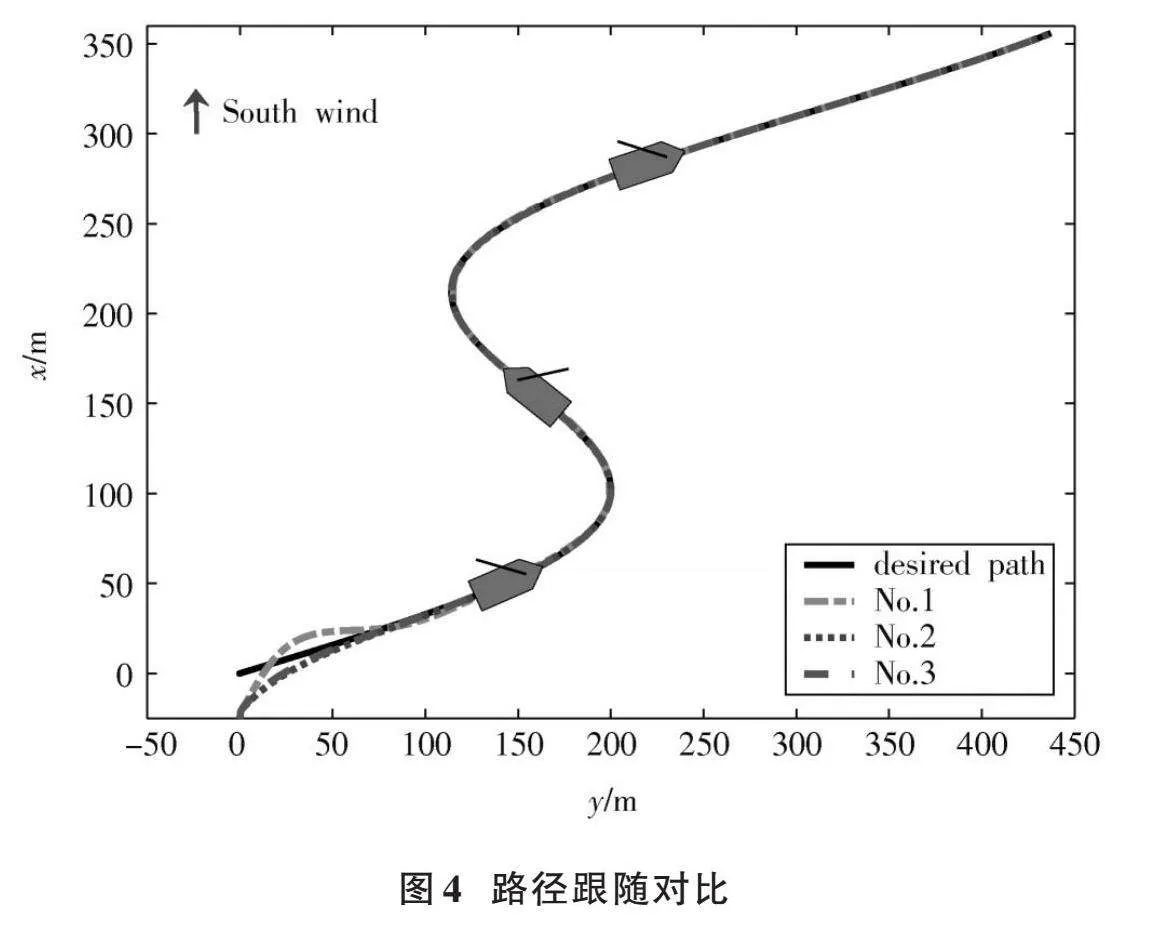
图4～图10为本文方法的仿真验证结果。

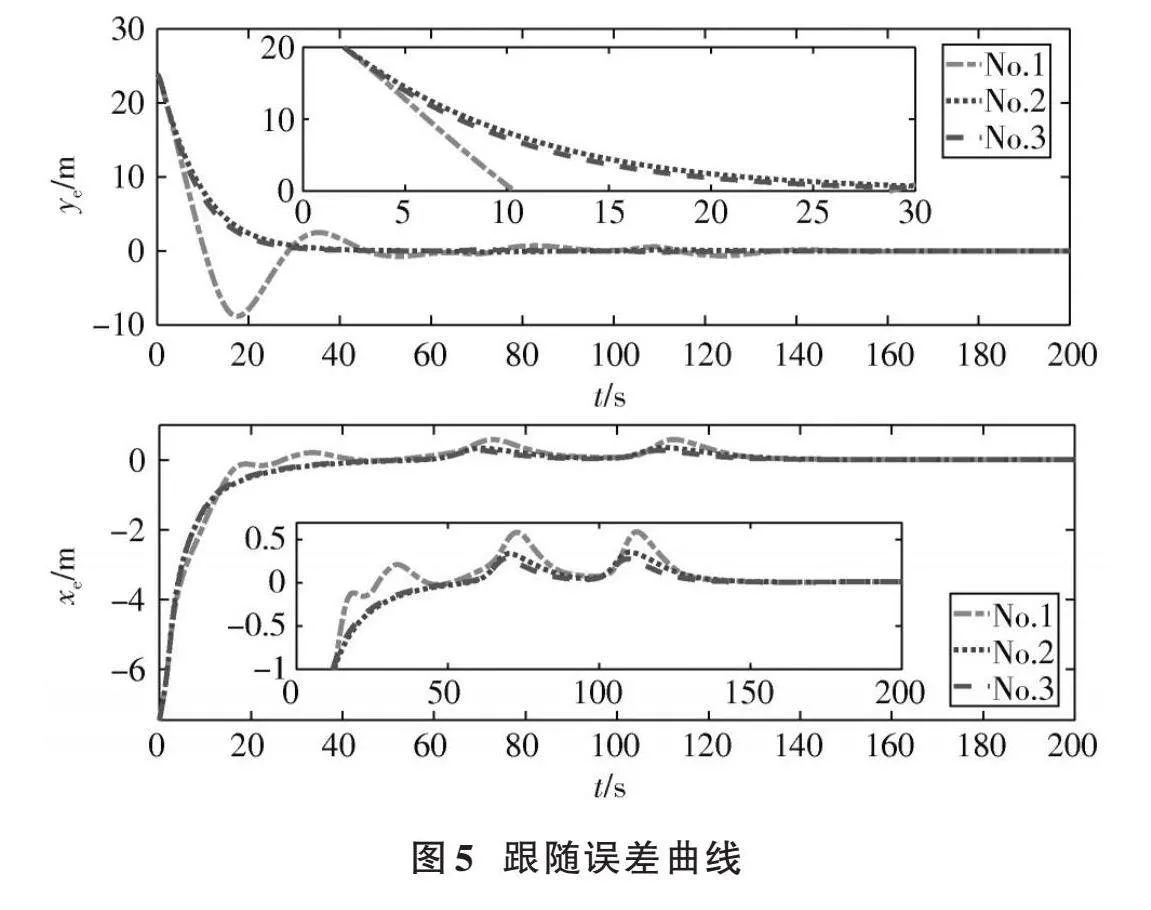
图4中3条小船分别代表了第45 s、第85 s和第140 s时的航行状态，图5所示本文制导方法要明显优于积分视线法，并且从横向误差和纵向误差来看，本文方法可以在短时间能收敛到零附近，达到更快稳定效果。

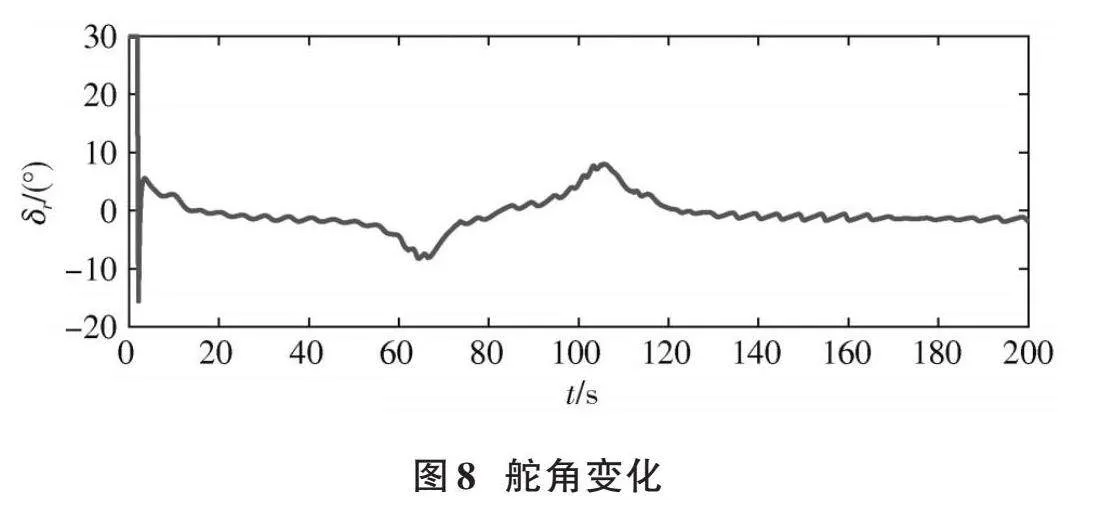
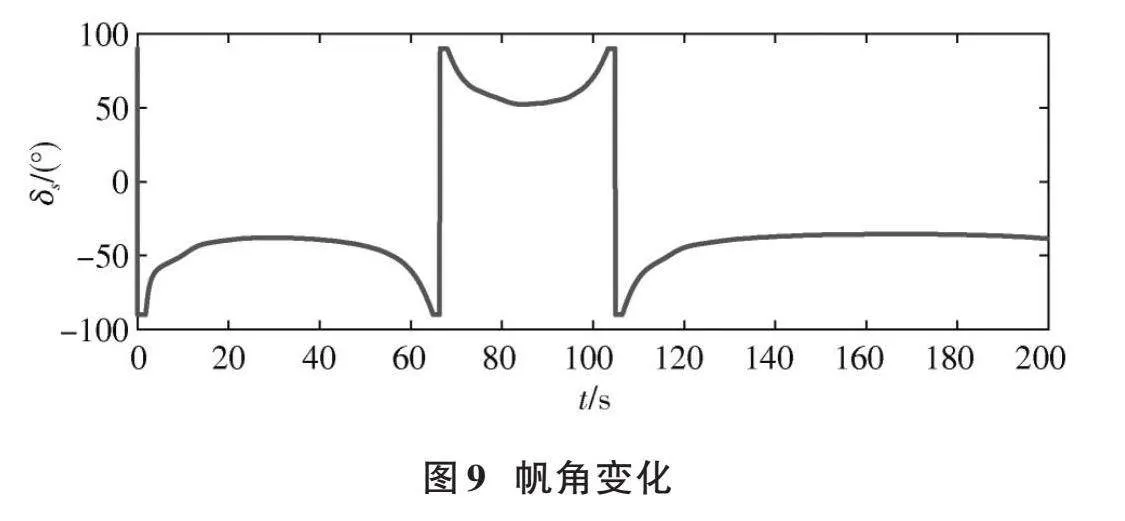
在图6中可以看出，所设计的反步控制方法具有良好的控制效果，航向误差可以快速收敛到零附近；在图7中漂角的观测误差也是在短时间内收敛；图8中舵控制器受外界风浪扰动的影响产生一定的抖动，舵角整体在0°附近调节，符合实际情况；图9显示帆角随着帆船与风的相对角度的改变而变化；图10显示了帆船航向中横倾角的变化。

5" 结" 论

本文针对无逆风航行条件下无人帆船的精确路径跟踪问题，提出了一种基于双有限时间侧滑角观测器的视线法制导方法。双有限时间观测器可以准确估计时变侧滑角，观测误差可以在短时间内收敛到原点。与ILOS和DELOS相比，本文方法具有更高的路径跟踪精度、更小的横向和纵向误差。在航向控制系统中，根据反步法和动态面滤波设计控制器，通过自适应参数估计模型受到的外部扰动。最后，通过仿真和比较，验证了本文方法的优越性和有效性。未来，考虑到帆船的长期作业，将从节能控制的角度研究帆船控制器，进一步优化风帆控制方法。

参考文献

[1] 俞建成，孙朝阳，张艾群.无人帆船研究现状与展望[J].机械工程学报，2018，54（24）：98⁃110.

[2] ABROUGUI H， NEJIM S， DALLAGI H. Modeling and autopilot design for an autonomous catamaran sailboat based on feedback linearization [C]// 2019 International Conference on Advanced Systems and Emergent Technologies （IC_ASET）. [S.l.： s.n.]， 2019： 130⁃135.

[3] CRUZ N A， AlVES J C. Auto⁃heading controller for an autonomous sailboat [C]// OCEANS 2010 IEEE. New York： IEEE， 2010： 1⁃6.

[4] LIN X， JEROME J. Modeling and nonlinear heading control of sailing yachts [J]. IEEE journal of oceanic engineering， 2014， 39（2）： 256⁃268.

[5] HE J X， XIAO L， JOUFFROY J. Towards heading control of an autonomous sailing platform through weight balancing [J]. IFAC proceedings volumes， 2012， 49（27）： 392⁃397.

[6] STELZER R， PRÖLL T， JOHN R I. Fuzzy logic control system for autonomous sailboats [C]// IEEE International Fuzzy Systems Conference. New York： IEEE， 2007： 1⁃6.

[7] 王倩，许劲松，徐建云.无人帆船循迹航行的控制研究[J].船舶工程，2015，37（9）：63⁃67.

[8] BORHAUG E， PAVLOV A， PETTERSEN K Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents [C]// IEEE Conference on Decision amp; Control. New York： IEEE， 2008： 4984⁃ 4991.

[9] FOSSEN T I， PETTERSEN K Y， GALEAZZI R. Line⁃of⁃sight path following for dubins paths with adaptive sideslip compensation of drift forces [J]. IEEE transactions on control systems technology， 2015， 23（2）： 820⁃827.

[10] LIU L， WANG D， PENG Z H. ESO⁃based line⁃of⁃sight guidance law for path following of underactuated marine surface vehicles with exact sideslip compensation [J]. IEEE journal of oceanic engineering， 2017， 42（2）： 477⁃487.

[11] MIAO J， WANG S P， TOMOVIC M M， et al. Compound line⁃of⁃sight nonlinear path following control of underactuated marine vehicles exposed to wind， waves， and ocean currents [J]. Nonlinear dynamics， 2017， 89（4）： 2441⁃2459.

[12] DENG Y J， ZHANG X K， ZHANG G Q. Line⁃of⁃sight⁃based guidance and adaptive neural path⁃following control for sailboats [J]. IEEE journal of oceanic engineering， 2019， 45（4）： 1177⁃1189.

[13] YU Y L， GUO C， LI T S. Finite⁃time LOS path following of unmanned surface vessels with time⁃varying sideslip angles and input saturation [J]. IEEE/ASME transactions on mechatronics， 2021， 27（1）： 463⁃474.

[14] FOSSEN T I. Handbook of marine craft hydrodynamics and motion control [M]. Hoboken， New Jersey： John Wiley amp; Sons， Inc.， 2011.