基于双指数的绝对辐射定标及FPGA设计与实现

摘" 要： 辐射定标技术是定量化遥感的关键环节，实时在轨绝对辐射定标已经成为在轨遥感数据实时智能处理的重要步骤之一。然而当前主流的星上定标、场地定标、交叉定标的定标算法以线性拟合方法为主，虽然计算简单，但是误差较大。文中提出一种基于双指数函数的绝对辐射定标方法，可有效提升定标计算精度，同时进行了FPGA硬件实现。针对输入数据数值超出Cordic计算模块的输入范围情况，提出对输入数值进行右移位实现整数除法操作以避免超范围的方法，并对输出结果进行多级自乘法运算实现了等效计算。通过FPGA仿真和在板运行，结果表明，当输入Cordic模块的数据小数位位宽设置为20 bit时，硬件计算的相对误差较小，仅0.030 3%。系统时钟工作在200 MHz时，处理能力达到2×108 f/s，满足实时应用要求。

关键词： 绝对辐射定标； 定量化遥感； 双指数函数； Cordic； FPGA； 多级自乘法运算

中图分类号： TN709⁃34； TP751.1" " " " " " " " "文献标识码： A" " " " " " " " " " " 文章编号： 1004⁃373X（2025）03⁃0149⁃06

Bi⁃exponential based absolute radiometric calibration

and FPGA design and implementation

LIU Youji1， SONG Beibei1， LI Bengbeng2， GAO Pan1， SUN Wenfang2

（1. School of Information Engineering， Chang’an University， Xi’an 710021， China;

2. School of Aerospace Science and Technology， Xidian University， Xi’an 710126， China）

Abstract： Radiometric calibration technology is a key step in quantitative remote sensing， and real⁃time on⁃orbit absolute radiometric calibration has become one of the important steps in real⁃time intelligent processing of on⁃orbit remote sensing data. However， the current mainstream calibration algorithms of on⁃orbit calibration， site calibration and cross⁃calibration are mainly based on the linear fitting method. The computation process of the method is simple， but its error is large. In this paper， an absolute radiometric calibration method based on double exponential function is proposed. The method can improve the accuracy of the calibration calculation effectively， as well as carry out the FPGA hardware implementation. In view of the fact that the input data value exceeds the input range of Cordic calculation module， a method of right shifting the input value to realize integer division operation for fear of exceeding the range is proposed， and the output result is subjected to multi⁃level self⁃multiplication to realize the equivalent calculation. The results of the FPGA simulation and on⁃board operation show that when the decimal bit width of the data input to the Cordic module is set to 20 bit， the relative error of the hardware calculation is small， only 0.030 3%. When the system clock works at 200 MHz， the processing capacity reaches 2×108 f/s， which meets the real⁃time application requirements.

Keywords： absolute radiometric calibration; quantitative remote sensing; double exponential function; Cordic; FPGA; multi⁃level self⁃multiplication operation

0" 引" 言

近几十年来，我国已经发射了超过60颗的民用对地观测卫星，形成了多个对地观测卫星体系，为农业、气象、测绘、环保等众多领域提供了大量的观测数据[1]。光学遥感卫星载荷辐射定标对于遥感数据定量化应用至关重要[2]。在轨卫星光学遥感探测系统的辐射定标主要包含相对辐射定标和绝对辐射定标两种。相对辐射定标是为了纠正传感器不同探元之间的响应差异，绝对辐射定标是为了将无量纲的图像DN（Digital Number）值（遥感影像像元亮度值，记录地物的灰度值）转换成光学传感器的入射辐射量或者温度等信息，并建立遥感相机输出信号值与输入辐射量或温度之间的函数关系。绝对辐射定标一般包括发射前定标和发射后的在轨定标。虽然发射前的实验室定标能够使用已知的辐射源，具有检查和解决发射前遥感载荷异常的优点，但在发射后的实际情况下，光学遥感载荷会受到振动和元器件老化等诸多因素的影响，无法保证传感器探测的长期准确性[3⁃4]。因此，常态化的在轨绝对辐射定标对于保证遥感数据质量具有重要作用。

目前已知的在轨辐射定标技术有星上定标、场地定标、交叉定标。星上定标利用定标灯光源、自然辐射源、黑体定标源以及太阳漫反射板等星载定标设备定标，具有高精度、高频次的优点。场地定标通过卫星过境时测量的地表和大气的参数与DN值拟合获得绝对定标所需的系数，主要包括辐照度基法、反射率基法和辐亮度基法。交叉定标利用已经定标且精度较高的卫星作为参考星对其他未定标的卫星进行定标[5⁃6]。无论是星上定标、场地定标还是交叉定标，目前大多数采用两点线性校正法、分段线性校正法进行定标参数计算。两点线性校正法操作和计算简单，但是误差较大。同时，两点法假设的是探元的响应曲线在响应范围内是线性的，然而一般情况下并非如此。因此，一般考虑采用的是分段的两点定标法，即分段线性法，其将探元的响应曲线合理地分成多个子段，每一段都近似地看成是线性的响应[7⁃10]。分段线性校正法能较好地拟合实际像元响应曲线，但是随着分段段数增加，定标参数的计算量和存储量也随之线性增加。为此，本文提出了一种双指数全范围定标方法，在使用较少的参数情况下可获得较高的计算精度，并进行了FPGA设计和加速计算，实现了遥感数据绝对辐射定标的实时处理。

1" 基于双指数拟合的绝对辐射定标方法

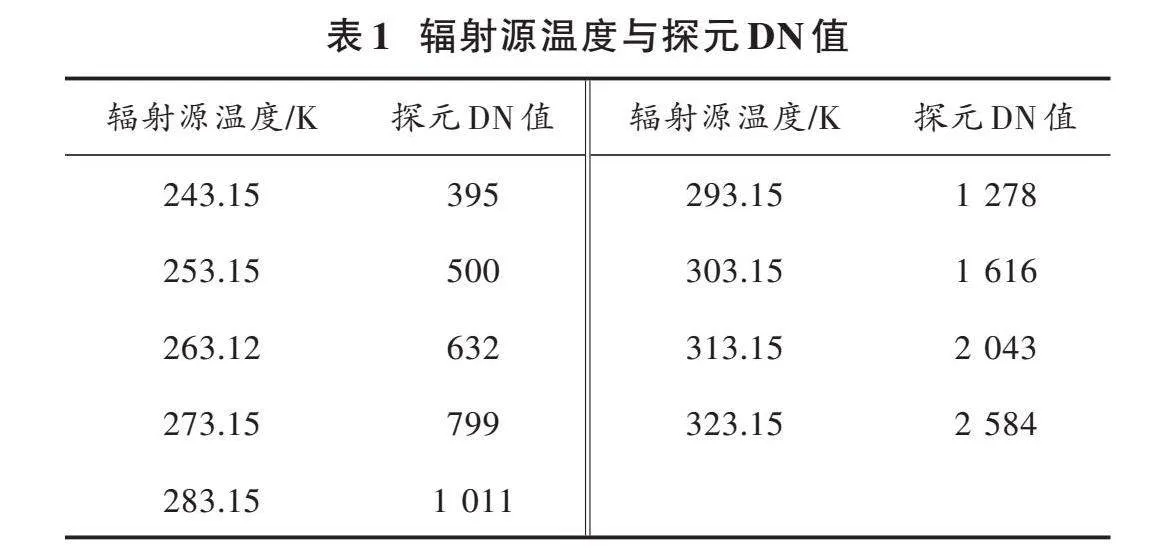
考虑到地表温度主要处于243.15（-30 ℃）～323.15 （50 ℃）K的范围，因此从243.15～323.15 K，每隔10 K给标准辐射源设置一个温度点，利用长波红外相机（12位采样精度）测得每个温度点情况下探元DN值的平均值，如表1所示。

分别采用两点线性拟合法[T1（DN）=a⋅DN+b]，多项式拟合法[T2（DN）=a0+a1⋅DN+a2⋅DN2]，以及双指数拟合法[T3（DN）=c1eb1⋅DN+c2eb2⋅DN]对表1测量数据进行曲线拟合，拟合曲线对比见图1，相对拟合误差分别为0.791%、1.96%、0.52%。因此双指数拟合法具有最好的拟合结果，其中，[c1]=283，[b1]=[5.26×10-5]，[c2]=-92.68，[b2=-1.798×10-3]。

2" 基于FPGA的绝对辐射定标方法设计

2.1" 总体方案设计

利用双指数定标方法进行绝对辐射定标，其组成为[T=c1eb1⋅DN+c2eb2⋅DN]。其中，[b1]、[b2]、[c1]、[c2]均为常量系数。绝对辐射定标FPGA实现的总体设计图如图2所示。

1） 首先输入DN值，DN值的范围在[0，212-1]，因此输入数据的位宽为12 bit。

2） 在使用双指数函数进行绝对辐射计算时，指数项的输入分别为[b1⋅DN]、[b2⋅DN]。设定[b1]、[b2]为常数，再与DN值分别进行相乘。在FPGA设计中采用一个有符号数的乘法器进行乘法计算。

3） 利用技术成熟的CORDIC IP核进行指数计算，分别得到[eb1⋅DN]、[eb2⋅DN]。

4） 采用乘法器对指数计算结果分别与系数[a1]、[a2]进行相乘，通过设置不同的小数位的位宽，可以获得不同的计算精度。

5） 用加法器相加得到最后的结果。

2.2" 基于CORDIC的指数计算

2.2.1" CORDIC指数计算原理

CORDIC又名坐标旋转数字计算方法，其主要原理是通过不断地旋转角度迭代来逼近计算的角度，计算中只涉及到加减法、查找表和移位操作[11⁃13]。本文采用CORDIC算法中的双曲线系统进行指数计算。

[ex=cosh（x）+sinh（x）] （1）

图3为双曲系统的矢量旋转图，向量[OP]与[x]半轴的夹角为[α]，[OQ]与[x]半轴的夹角为[β]。将向量[OP]绕原点[O]逆时针旋转[θ]角得到向量[OQ]。因此，[P]点和[Q]点的坐标可以分别表示为：

[P：x1=cosh（α）y1=sinh（α）Q：x2=cosh（β）=cosh（α+θ）y2=sinh（β）=sinh（α+θ）] （2）

式中[θ]为目标旋转角。

再根据双曲旋转公式，将式（2）展开：

[x2=cosh（α+θ）=cosh（α）⋅cosh（θ）+sinh（α）⋅sinh（θ）y2=sinh（α+θ）=sinh（α）⋅cosh（θ）+cosh（α）⋅sinh（θ）] （3）

再将[P]点代入式（3）中，得到式（4）：

[x2=x1⋅cosh（θ）+y1⋅sinh（θ）=cosh（θ）⋅（x1+y1⋅tanh（θ））y2=x1⋅sinh（θ）+y1⋅cosh（θ）=cosh（θ）⋅（y1+x1⋅tanh（θ））] （4）

CORDIC算法的核心就是使用迭代的方法，每次旋转一小角度来逼近最终的目标角度，于是可以将[θ]拆分为[θi]的组合。假设每次旋转的方向用[di]来表示，[di=1]表示逆时针旋转，[di=-1]表示顺时针旋转。因此，[θ=i=1ndiθi]。FPGA在设计上容易通过移位操作来实现乘2和除2计算，[tanh（θi）=2-i]，即有[θi=atanh（2-i）]。采用旋转模式进行迭代计算[14]，其过程如下：

[xi+1=cosh（θi）⋅（xi+di⋅yi⋅2-i）yi+1=cosh（θi）⋅（yi+di⋅xi⋅2-i）zi+1=zi-di⋅θi] （5）

式中[zi+1]表示第[i]次旋转之后剩余的角度。通过[N]次迭代之后，就可得到最终的[（xθ，yθ）]。

2.2.2" 基于FPGA的CORDIC计算

为了使硬件资源和计算速度达到最佳平衡，以及更加方便快捷的设计，采用CORDIC IP核进行指数计算。首先将CORDIC IP核函数设置为sinh和cosh，利用面积换取速度的思想，选择并行处理的架构，并将流水线设置为最优，以尽可能多地使用流水线级数从而加快计算速度[15]。输入数据和输出数据位宽相同，格式均设置为有符号小数，最高位为符号位。对于输入数据，整数位有两位，其余为小数位，而对于输出数据，其整数位仅一位。角度系数设置为以弧度为单位，计算的取整模式设置为四舍五入。

然而使用CORDIC IP计算双指数函数的难点在于CORDIC IP核要求输入数据的数值范围在[-14π，14π]，但存在[DN∈0，4 095]与[b2]相乘后超出该范围的情况。为此，针对性地提出了一种避免输入数值超出允许范围的设计方法。

当[b2⋅DN]超出输入范围时，将其平均等分成[n]个满足输入范围的数值[w⋅DN]，即[b2⋅DN=n⋅w⋅DN]。考虑到FPGA实现除法计算复杂度高，于是当[DN∈（400，800]]时，[n]取值为2；当[DN∈（800，1 500]]时，[n]取值为4；当[DN∈（1 500，3 000]]时，[n]取值为8；而当[DN∈（3 000，4 095]]时，[n]取值为16。然后直接采用移位操作便能实现等分除法处理，有效降低了计算硬件资源消耗。又因为[eb2⋅DN=en⋅w⋅DN=i=1new⋅DN]，所以将计算得到的指数结果[ew⋅DN]进行[n]次自相乘就能得到[eb2⋅DN]。在FPGA设计时，先将[b2]进行移位操作再与DN值进行相乘，然后根据等分参数[n]取值4、8、16，分别设置2、3、4级流水线计算[n]次自相乘，有效增加了计算处理速度。改进后的设计方案如图4所示。

CORDIC IP核输出[cosh（x）]和[sinh（x）]的计算数值，最后将[sinh（x）]和[cosh（x）]用一个有符号数的加法器进行加法计算便可得到[ex]。

3" 实验结果与分析

3.1" 软硬件计算误差分析

使用Vivado 2018.3按照图4提出的改进方法进行FPGA程序设计，综合得到的RTL结构如图5所示。

导出FPGA仿真文件计算出的结果，与Matlab仿真结果进行比较，得到不同DN值下的相对计算误差。图6分别给出了输入数据小数位位宽从17～20 bit的相对误差结果比较。

从图6中可以看出，FPGA仿真的结果与Matlab仿真的结果之间的相对误差与DN值呈高度线性关系。当DN值较小时，指数输入的值也很小，此时指数计算的误差较小。

而当DN值越来越大时，指数的输入值也随之增大，指数计算误差也随之增大。

3.2" FPGA硬件资源与时序分析

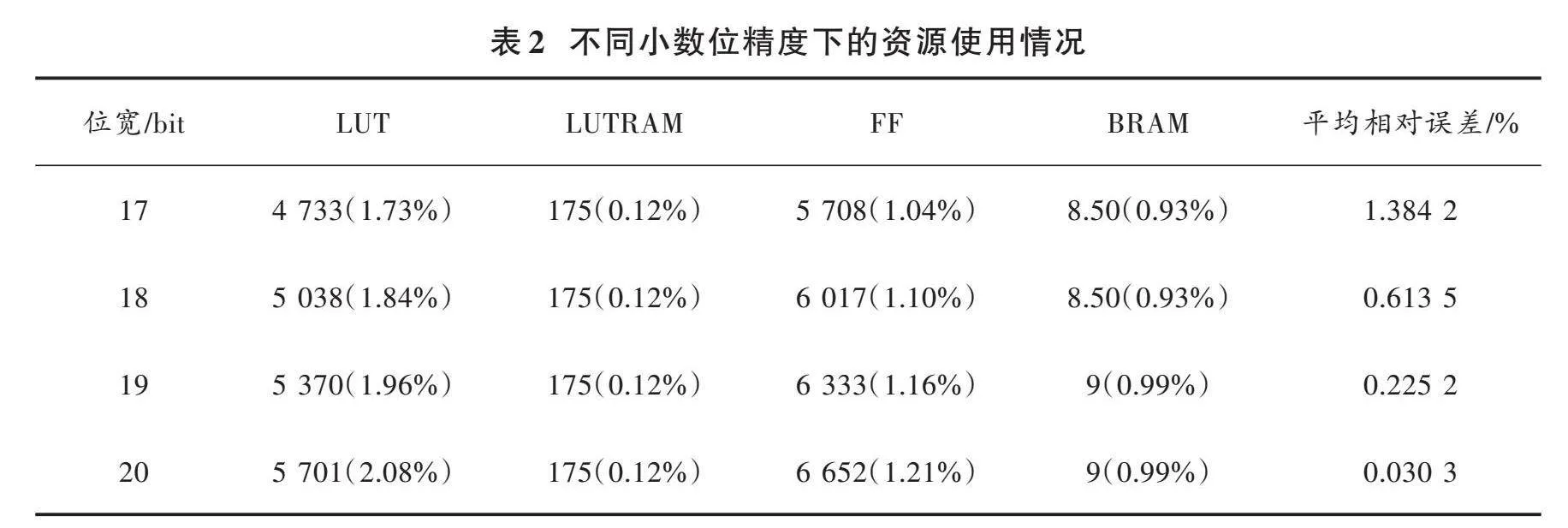
将设计的FPGA程序综合成bit文件运行在Xilinx公司的XCZU9EG FPGA芯片上，系统运行时钟为200 MHz。在FPGA工程中加入ILA核，通过ILA核实时抓取在板计算结果，并与Matlab仿真结果进行比较。表2分别给出了输入数据小数位位宽从17～20 bit的硬件资源消耗和平均相对误差结果比较。

从表2中可以看出整体方案所使用的各资源用量相对较小。同时可以看出随着小数位位宽的增大，LUT、FF、BRAM资源消耗在小幅增加，而LUTRAM消耗保持不变。当小数位位宽增加时，平均相对误差也越来越小，当输入数据的小数位位宽达到20 bit时平均相对误差最小。小数位位宽越大，计算精度越高，随之必然会带来硬件资源消耗的增加。

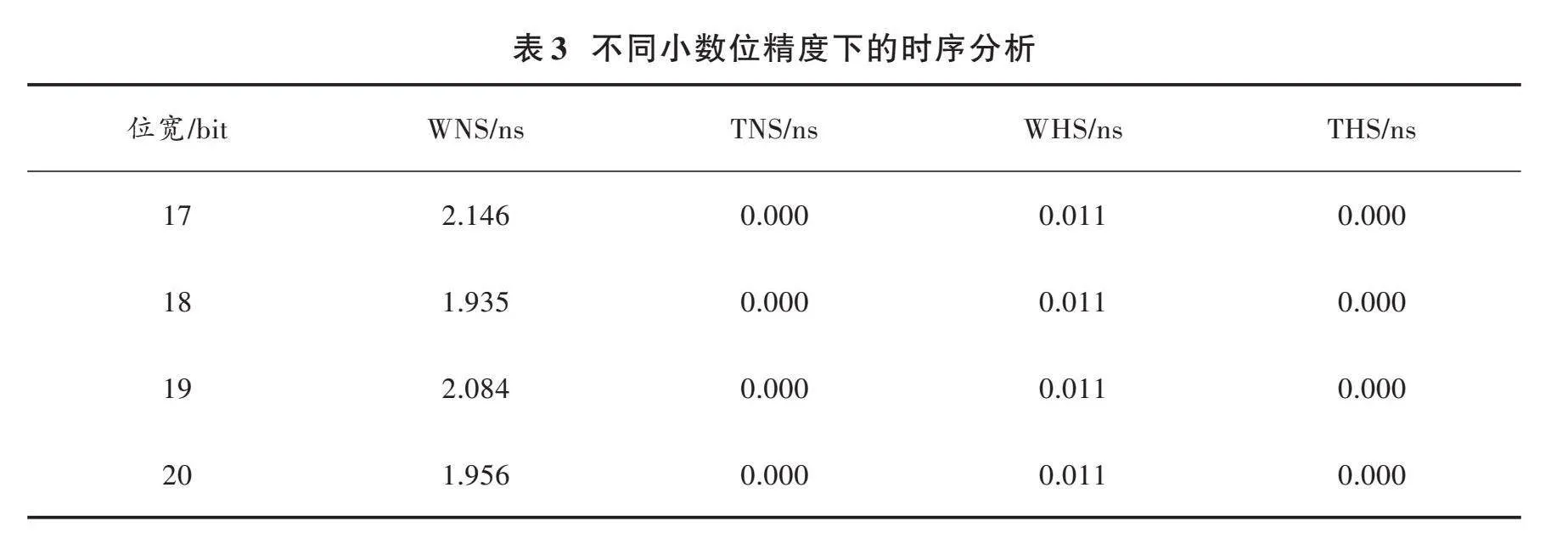
表3展示了小数位位宽从17～20 bit之间不同的时序情况。其中：WNS表示最差负时序裕量；TNS表示总的负时序裕量；WHS表示最差保持时序裕量；THS表示总的保持时序裕量。WNS、TNS、WHS、THS均为正值，表示时序正常，没有时序违例。

4" 结" 论

本文通过软件模拟仿真实验验证了双指数绝对辐射定标高精度拟合优势，并进行了FPGA设计和实现。实验结果表明，增加小数位位宽可以保证计算精度，但同时小幅增加了对硬件资源的消耗，在20 bit的小数位位宽时达到精度和资源消耗的权衡。近几年，农业、气象、环保等用户对红外光谱图像的定量化应用逐步增加，因此对于定标精度的需求也越来越高。本文提出的方法保证了辐射定标精度的同时，消耗硬件资源总体较小，从而提高了系统的效率和性能。基于双指数的绝对辐射定标方法在对地观测遥感卫星的星上在轨处理中具有潜在的应用前景。

参考文献

[1] 马灵玲，王宁，高彩霞，等.光学遥感卫星在轨绝对辐射定标：进展与趋势[J].遥感学报，2023，27（5）：1061⁃1087.

[2] 高海亮，顾行发，余涛，等.星载光学遥感器可见近红外通道辐射定标研究进展[J].遥感信息，2010（4）：117⁃128.

[3] 张玉环.HJ1⁃CCD交叉辐射定标[D].青岛：山东科技大学，2012.

[4] 满益云，陈世平.光学遥感卫星在轨星上绝对辐射定标的研究进展[J].中国空间科学技术，2022，42（6）：12⁃22.

[5] 刘李，顾行发，余涛，等.HJ⁃1B卫星热红外通道在轨场地定标与验证[J].红外与激光工程，2012，41（5）：1119⁃1125.

[6] 孙珂，傅俏燕，亓学勇.HJ⁃1B卫星IRS传感器热红外通道交叉标定[J].红外与激光工程，2010，39（5）：785⁃790.

[7] 吕原，丛明煜，赵旖旎，等.红外相机实时绝对辐射定标技术研究[J].红外与激光工程，2022，51（7）：106⁃119.

[8] 王海燕，于晋，李照洲.星载红外相机相对定标算法研究[J].航天返回与遥感，2009，30（2）：44⁃49.

[9] 赵艳华，李云飞，王浩.长波红外相机真空辐射定标试验不同状态影响研究[C]//第八届高分辨率对地观测学术年会论文集.北京：北京空间机电研究所，2022：843⁃854.

[10] 杨词银，张建萍.一种中波红外相机的定标[C]//中国光学学会.中国光学学会2010年光学大会论文集.天津：中国科学院长春光学精密机械与物理研究所，2010：3943⁃3947.

[11] 牟胜梅，李兆刚.一种面向FPGA的指/对数函数求值算法[J].计算机工程与应用，2011，47（33）：59⁃61.

[12] REKHA R， MENON K P. FPGA implementation of exponential function using cordic IP core for extended input range [C]// 3rd IEEE International Conference on Recent Trends in Electronics， Information amp; Communication Technology （RTEICT）. New York： IEEE， 2018： 597⁃600.

[13] ZHANG W Y， ZHANG C， NIU L T， et al. An efficient FPGA design for fixed⁃point exponential calculation [C]// 2022 IEEE International Conference on Integrated Circuits， Technologies and Applications （ICTA）. New York： IEEE， 2022： 44⁃45.

[14] 姚亚峰，杨金岷，周群群，等.高精度低消耗CORDIC算法设计[J].湖南大学学报（自然科学版），2023，50（12）：69⁃75.

[15] 张华军，赵金，丛吉吉.CORDIC在基于FPGA的神经网络设计中的应用[J].华中科技大学学报（自然科学版），2009，37（6）：36⁃39.

[16] 姚源，刘齐悦.大口径中波红外辐射特性测量系统标定[J].电子设计工程，2022，30（2）：115⁃119.