一种LuGre摩擦模型自适应补偿的分析及仿真

刘东升　白桦　李文君　宋发兴

摘要：介绍一种降低低速转台伺服系统在转动过程中由于摩擦因数影响转动精度的方法。在低速转台转动的过程中由于摩擦力等的影响，转台的速度、位置都会发生偏差，所以在转台系统上引入摩擦控制补偿。利用公式推理，通过与理论值对比，发现自适应摩擦补偿方式与传统摩擦补偿方式相比，其跟踪误差大大降低，能有效抑制摩擦干扰对伺服系统的不利影响。进行基于MATLAB环境下的仿真效果。

关键词：摩擦模型；摩擦补偿；自适应控制

中图分类号：TP27 文献标识码：A

1引言

转台伺服系统低速时的速度精度和速度平稳性是评价转台性能好坏的重要标志之一，由于转台伺服系统是以经纬度为引导信息，它的位置精度、速度精度和速度平稳性直接影响转台所搭载的天线的跟踪效果，尤其影响转台系统的低速性能指标。影响系统低速性能的因素很多，有摩擦力矩，电机波动力矩，测速机的灵敏度，控制系统采样等。其中最主要的因素是摩擦力矩和电机波动力矩，是摩擦力矩和电机波动力矩造成了转台低速运行时的爬行现象、精密定位时的抖动现象以及稳态时有较大的静差或出现极限环震荡。由于实际系统都是非线性系统，转台在低速运转时，输入信号较小，其低速的性能主要取决于非线性因素。其中摩擦力矩是影响性能的主要原因。因此对摩擦力矩进行建模分析，并针对模型进行补偿研究，对提高转台性能有着重要意义。

2伺服系统的LuGre摩擦模型

在伺服系统中，无论从摩擦现象的角度出发，还是从对其补偿的角度出发，对非线性环节建立准确的数学模型，其都是很重要的。已建立的摩擦模型很多，有Karnopp模型、LuGre模型以及综合模型。其中，LuGre模型是Canudas等在1995年提出的典型伺服系统摩擦模型，此模型对摩擦过程复杂的动态、静态特性描述准确，如爬行、极限环振荡、滑前变形、摩擦记忆及静态Stribeck曲线。此模型描述如下：

对于伺服系统，用式（1）表示：

其中，J为转动惯量，θ为转角，μ为控制力矩，F为摩擦力矩。设变量Z代表接触面鬃毛变形，则F可由下面的LurGre模型来描述：

式中，σ₀、σ₁，称为动态摩擦参数，F_c、F_s、α、V_s称为静态摩擦参数，其中，F_c为库仑摩擦，F_s为静摩擦，a为粘性摩擦系数，V_s为切换速度。

2.1基于LurGre摩擦模型的PID控制补偿

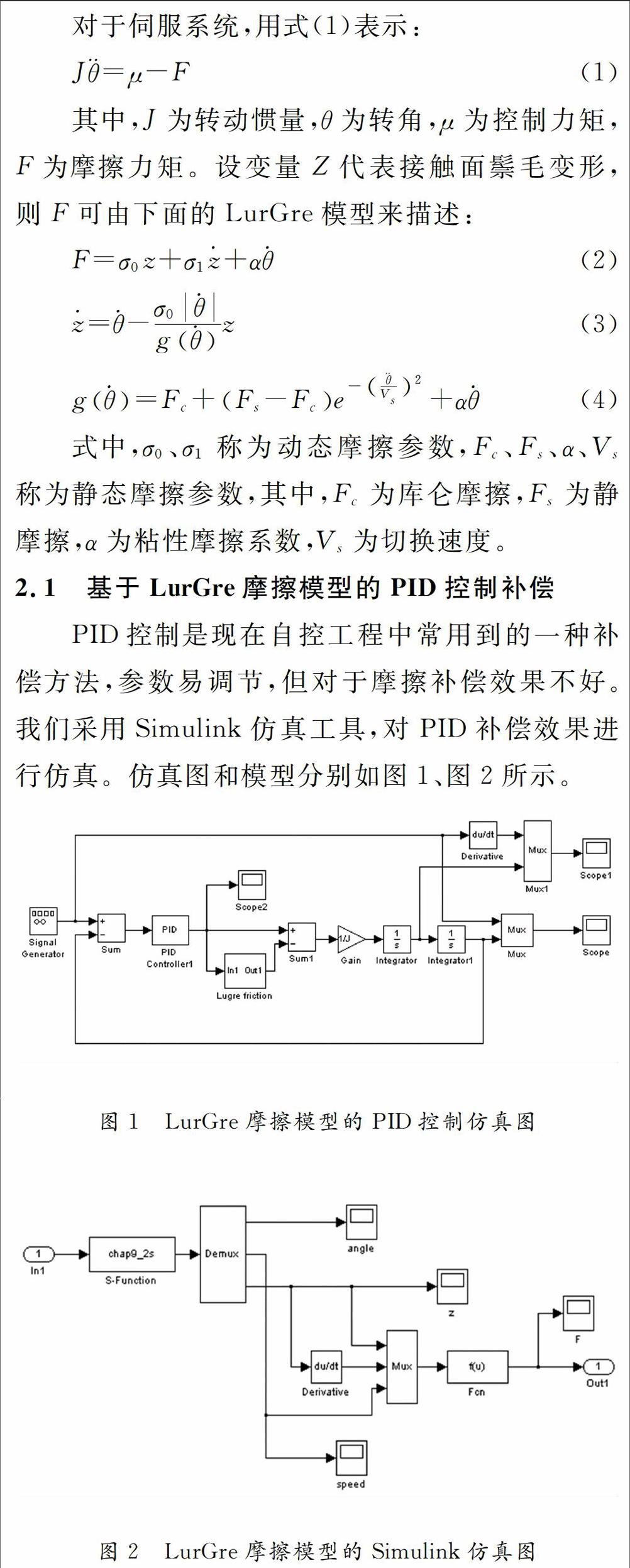
PID控制是现在自控工程中常用到的一种补偿方法，参数易调节，但对于摩擦补偿效果不好。我们采用Simulink仿真工具，对PID补偿效果进行仿真。仿真图和模型分别如图1、图2所示。

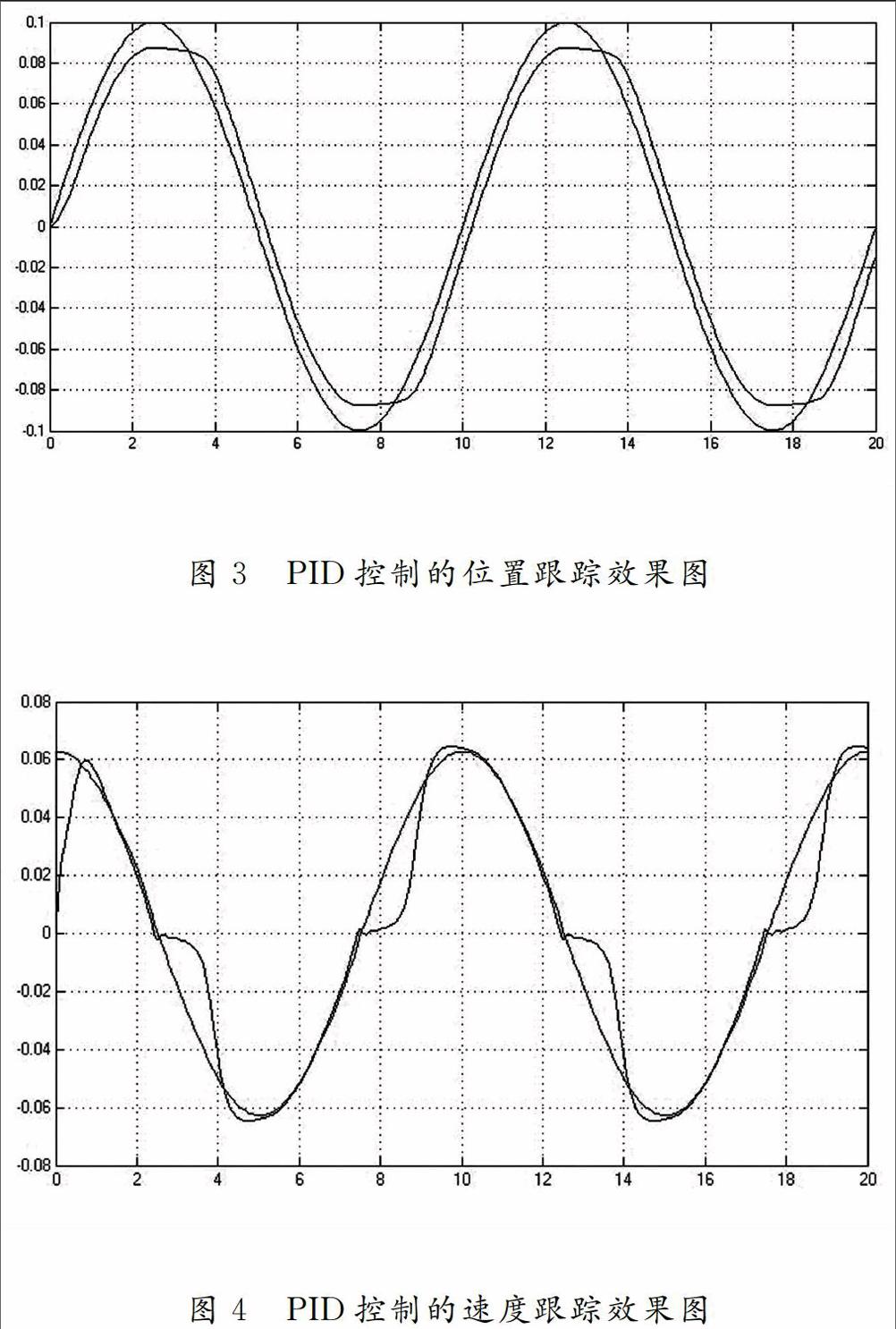
根据伺服系统式（1）及摩擦模型式（2）～式（4），取J=1.0，σ₀-260，σ₁=2.5，α=0.02，F_s=0.34，V_s=0.01。输入位置指令r（t）=0.1sin（0.2πt）。采用PID控制，取K_p=20，K_d=5.0，仿真时间为20s。其位置和速度跟踪效果如图3、图4所示。

从图3、图4的仿真结果看出，在带摩擦的条件下，采用PID控制对其进行补偿，其位置有“平顶”现象，速度跟踪有“死区”现象，控制的鲁棒性较差，不能满足高精度跟踪要求。因此必须对LuGre摩擦模型采用更好的补偿方法。

2.2基于LuGre摩擦模型的自适应补偿

2.2.1基于LuGre摩擦模型的自适应补偿设计

由于LuGre模型中有一个不确定的状态量Z。在实际中，常用观测器对其观测，根据观测结果对伺服系统实现摩擦补偿，有助于伺服系统性能的提高。该模型包含LuGre动态模型和自适应控制器，控制器包含参数的自适应律和等效PID控制律，用来估计未知LuGre参数，从而给予补偿。最后采用了Lyapunov方法证明，该方法能满足对期望位置信号的渐近跟踪。如图5所示典型电机系统。

由图5系统模型，可得系统动态方程：

其中σ、σ₀、σ₁是自适应补偿参数，自适应补偿的重点是设计一个非线性的控制器来补偿这些参数的变化。对于位置跟踪控制，系统误差方程为：

θ_d（t）为期望位置信号，其两阶可导，k为正值的反馈增益，e₁（t）为位置跟踪误差。将式（12）代入式（13）得：

可以看出Lyapunov函数导数是非正函数，可以保证误差e₂，观测器误差z₀、z₁以及未知参数误差σ、σ₀、σ₀一致有界，由e₁、e₂得知，e₁保证有界，根据期望信号θ_d、θ_ed的定义，可以保证θ_ed、θ、θ一致有界；根据摩擦估计误差定义，可以得到摩擦状态Z一致有界，进一步估计，一致有界，从而得到控制规律U₁的有界性。

2.2.2基于LuGre摩擦模型的自适应补偿仿真

基于LuGre摩擦模型的自适应补偿的simu-link仿真如图6所示。其中取相关补偿参数c=10，β₀=150，β₁=50，β=55。

假定正弦叠加信号，通过自适应补偿模型，观测该信号位置和速度补偿效果，结果表明，LuGre摩擦模型的自适应补偿在很大程度上减小了摩擦的影响，基本清除了位置跟踪的“平顶”和速度跟踪的“死区”现象，从而提高了位置、速度的跟踪精度。其稳态误差可控制在1.7*10^-3。左右。位置跟踪和速度跟踪效果分别如图7和图8所示。

3结束语

在低速转台的转动过程中，由于摩擦因素的影响，必须引入补偿系统，给予补偿。经过比较分析，得到基于LuGre摩擦模型的自适应补偿系统是最适合本低速转台伺服系统的，有助于伺服系统性能的提高。最后采用了计算机仿真方法证明，该方法能保证对期望位置信号的渐近跟踪。合理选择分析参数，完全可以使跟踪结果在试验误差允许范围内。