MIMO网络控制系统的稳定性与控制器设计

马飞　赵立英

摘要：对于具有多个独立传感器与执行器的多输入多输出网络控制系统，在具有多重时滞的情况下，建立一类网络控制系统的连续时间模型。通过构造一个新的李雅普诺夫函数，给出一个具有较低保守性的稳定性判据。基于该稳定性判据，给出输出反馈控制器的设计方法，数值仿真结果表明了该方法的有效性。

关键词：网络控制系统；稳定性；时滞；线性矩阵不等式

中图分类号：TP273 文献标识码：A

1引言

网络控制系统又被称为基于网络的控制系统、网络化控制系统，是一种完全网络化、分布化的控制系统，是通过网络构成闭环的反馈控制系统。如今，控制系统的规模越来越大，其程度的复杂性也越来越高，系统的物理设备和功能也在不断的扩充。传统的点对点直接连接方式已经达到了自身应用的极限，无法满足系统功能不断增长的需求。例如，在一个大型的工厂车间内，各个单元和生产线常分布于工厂各处，所有设备作为一个整体可看做是一个被控对象分散的控制系统。如果采用传统的点对点方式进行控制，则需要大量的连接专线，耗费巨大的电力和水力资源。显然，这样的工厂每天运行所耗费的成本是昂贵的。随着电子技术和计算机技术的不断发展，很多网络传输方式被应用到控制领域中。网络控制系统随之应运而生。

网络控制系统作为一门崭新的学科，是网络通信技术和自动化控制技术两个学术领域的交叉融合，具有其特殊性和复杂性。控制领域研究的内容主要是基于一定服务质量的控制网络，研究系统的控制策略和控制技术，以期提高控制系统的性能；而通信领域学者研究的内容主要是设计合适的通信协议和调度方法，以期提高网络本身的服务质量。未来的发展趋势是控制与通信的一体化设计。研究网络控制理论和控制方法既具有重要的学术价值，又具有可观的经济效益。

近年来，网络控制系统的研究受到广泛的关注。与传统点对点互连的控制系统相比，网络控制系统的主要优点为网络布线方便，连接线数大大减少，易于扩展，成本低，易安装、故障检修和维护方便，抗干扰性强，数据传输可靠性高、实现信息资源共享等优点。但是这样就不可避免的将网络传输时滞引入系统中，它会降低控制系统的性能甚至导致系统不稳定，从而使网络控制系统的分析与设计变得更加复杂。网络时延是系统设计和实现的突出问题。

本文研究一类MIMO网络控制系统时滞相关稳定性问题。文献阳研究了此类问题。本文首先建立了一类MIMO网络控制系统新的模型，通过构造新的Lyapunov函数，引入适当的自由权矩阵，利用线性矩阵不等式与稳定性理论，得到系统依赖于时滞大小的渐进稳定的条件。基于已获得的稳定性的条件，提供了一种状态输出反馈控制器设计的方法。

2系统建模与问题描述

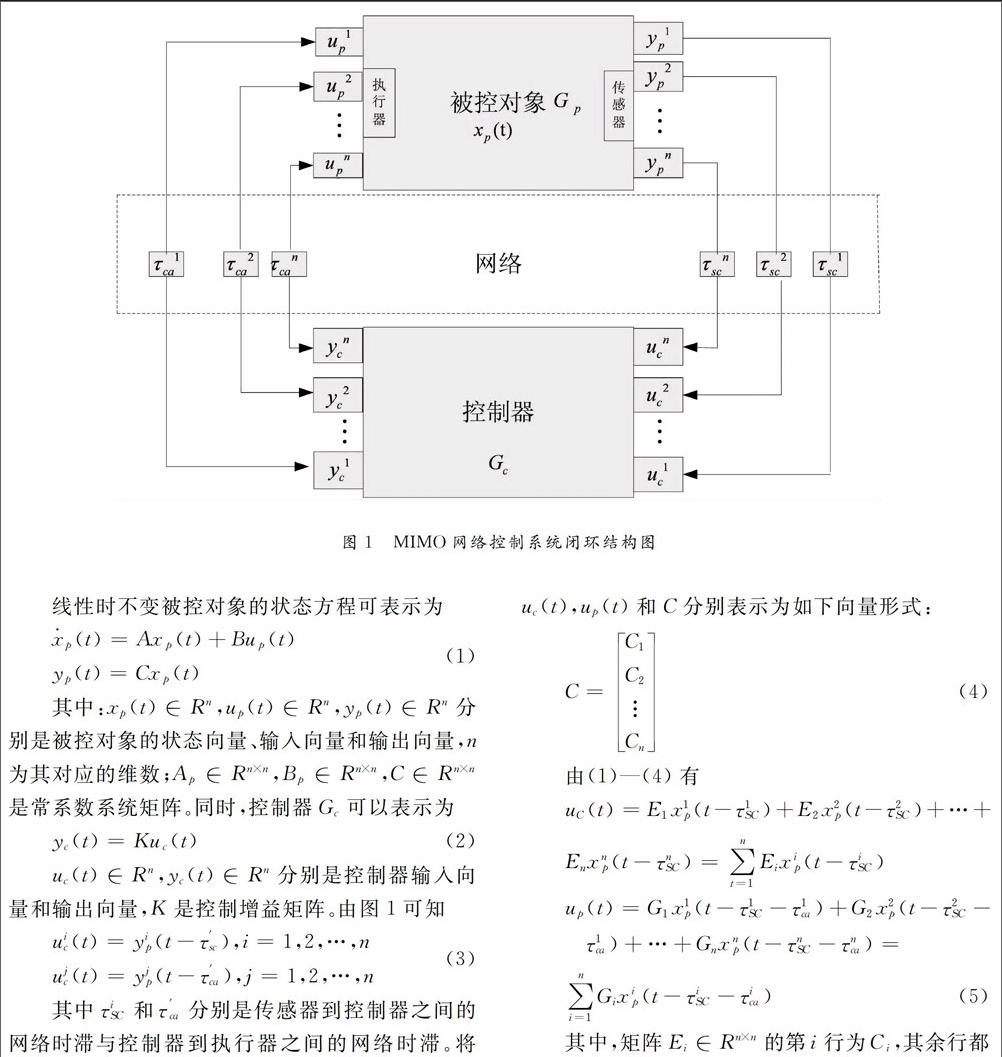
考虑一类连续的MIMO网络控制系统，该系统有多个独立的传感器与控制器。其闭环结构如图1所示：

线性时不变被控对象的状态方程可表示为别是被控对象的状态向量、输入向量和输出向量，n为其对应的维数；A_p∈R^n×n，B_p∈R^n×n，C∈R^n×n是常系数系统矩阵。同时，控制器G_c可以表示为

u_c（t）∈Rⁿ，y_c（t）∈Rⁿ分别是控制器输入向量和输出向量，K是控制增益矩阵。由图1可知为零向量，矩阵G_i∈^n×n的第i行为K_iC_i，其余行都为零向量。则系统可以表示为

3MIMO网络控制系统的稳定性分析与控制器设计

3.1稳定性分析

本节基于构造新的lyapunov函数来分析MIMO网络控制系统（7）的稳定性。

定理1：如果存在矩阵P>0，Q>0，

（i=1，2，…，n）和适当维数的矩阵S_i>0，

（i=1，2，…，n）使得下列LMI：

4仿真实例

为验证本文方法的有效性，采用文献中的例子和方法进行验证。

图2为2阶闭环系统输出反馈响应曲线，通过该图像，在所设计的控制器的反馈下，原系统实现了比较好的镇定。

5总结

本文研究了具有多时滞的MIMO网络控制系统的稳定性分析与控制器设计，通过构造一种新的laypunov函数，利用线性矩阵不等式，给出了系统稳定性的判据和控制器的设计方法。与文献相比，本文方法的保守性比较低，时滞的范围更大。与文献相比，本文给出了控制器设计的方法。仿真结果表明了该方法的有效性。