数形结合思想在解题中的应用策略

摘 要：数学是研究数量关系和空间形式的科学，“数”与“形”是数学的研究对象.借助“形”可以使“数”更加直观，借助“数”可以使“形”更加精确，数形结合是中学数学中极其重要的数学解题方法.基于此，文章从“以形助数”和“以数解形”两个方面阐述数形结合在解题中的应用策略，并以“鸡兔同笼”问题为例，给出具体的解题实例.

关键词：数形结合；解题方法；鸡兔同笼

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）32-0017-03

收稿日期：2024-08-15

作者简介：倪萌（1999.12—），女，安徽省六安人，硕士，从事数学解题教学研究.

数形结合思想对数学学习至关重要.“形”可直观呈现数量关系，“数”则精确描述形态特征，两者相辅相成，有助于深化学生对数学知识的理解.数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过以“形”助“数”或以“数”解“形”，复杂问题可以简单化、抽象问题可以具体化^[1].数形结合的应用大致可分为两种情形，一是借助“形”的几何直观性阐明“数”之间的某种关系，即“以形助数”；二是借助于“数”的精确性阐明“形”的某些属性，即“以数解形”^[2].笔者以鸡兔同笼问题为例，说明数形结合思想在解题中的应用策略.

1 数形结合思想概述

1.1 以“形”助“数”

根据希尔伯特公理体系，“形”的基本对象为点、线、面.以“形”助“数”即利用点、线、面，以直观的“形”帮助学生理解抽象的“数”，运用几何方法解决代数问题.数学中许多概念，比如图形、函数、方程等，往往与现实世界中的具体事物相对应.通过以“形”助“数”，可以更加直观地理解这些概念及其之间的关系，从而更好地掌握数学知识.中学数学是学生初步认识几何与代数的基础学科，受学生认知水平的限制，数学的直观性处于非常重要的地位.在中学阶段，数学概念、定理、公式等的学习，大多会选择借助“形”的辅助.根据从数学符号语言到图形语言的转化难度，其可分为直译、转译和建模.

1.1.1 直译

在中学数学中，直译是以“形”助“数”最简单直接的方法.其主要是利用“数”的几何意义将抽象的数值转化为几何图形的形状，从而使“数”更具体化、可视化，同时也可以帮助学生更好地理解和应用数学概念.例如，整数可以表示为数轴上的点，点的位置代表了整数的大小和符号；分数则可以表示为图形的比例关系或者平面图形的面积比例；乘方和根号分别可以表示为立方体的体积比例和平方面积和边长之间的关系，以及函数与其对应的图象等.另外，当需要找到数值之间的关系和变化规律时，可以将这些数值以可视化的方式展示出来，如作图、绘制表格等，通过直观地观察和分析，发现其变化规律.将“数”的抽象概念转化为几何图形是中学数学中一种非常实用的方法，可以帮助学生更加深入地理解数学概念和公式，建立几何代数整体认知，提升学生的数学应用能力.

1.1.2 转译

“数”和“形”之间的相互转换有时不是一件轻而易举的事情.在数学学习中，也存在不能将符号语言直接翻译为图形语言的情况，需要经过一定的转化来实现由“数”及“形”，而“数”所呈现的不同形式将会影响转化的效率.“数”具有抽象性，几何特征不明显或与标准式存在差异时，几何意义会被“杂乱”的“数”所掩盖，这时就需要进行适当调整，使几何意义浮出水面，以实现以“形”助“数”，即转译.转译需要学生深入理解“数”的几何意义，在数学学习中可以借助具体的图形、形状、尺寸等几何元素，帮助学生更加直观地理解“数”的抽象.同时，注重拓展学生的数学思维，培养学生的数形结合意识，合理利用“形”工具理解“数”对象.

1.1.3 建模

数学学习要从本质上认识和理解规律，学会寻找“数”与“形”之间的本质与联系，从特殊到一般，发展抽象思维能力和数学建模能力.大胆假设，小心求证，探索“数”与“形”之间的联系，自主尝试建立与“数”对应的“形”，构建数学模型解决数学问题.建模是具有一定难度的，但其过程有助于培养学生数学思维的广度和深度.

1.2 以数解形

“数”抽象而形式化，“形”具体而形象化.“形”虽具有形象直观的优势，但也有其粗略、烦琐和不便于表达的劣势.例如，求2^x=x²解的个数^[3].可将其转化为几何问题，求解过程就是通过绘制函数y=2^x与函数y=x²的图象，确定两者的交点个数.然而，在作图中会发现，图象的精确度会直接影响结果.若粗略作图，易得到错误答案，这时就需要以“数”解“形”，更准确地把握“形”.

在中学数学学习中，利用纯几何方法解决问题相对复杂时，可将几何的“量”数量化，几何的“点”坐标化，几何的“线性”方程化，几何元素间的关系等式或不等式化，从而将所研究的几何问题转化成代数、向量等问题，即以“数”解“形”.因此，实现以“数”解“形”的关键是建立平面直角坐标系，将“形”放到平面直角坐标系中，即可以转化为“数”，从几何问题转化为代数问题.

2 解题实践

“鸡兔同笼”问题是我国古代著名数学趣题.大约在1 500年前，《孙子算经》中就记载了这个问题，原文为：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？^[4]”

2.1 直译法

在不同版本的数学教材中，“鸡兔同笼”问题都安排在了小学学段，这阶段学生所学的几何方面的知识主要是认识基本的平面图形和立体图形，数学思维水平较低，以直观认识为主.所以对于“鸡兔同笼”问题，结合的“形”，常常较为具体，贴切于实际的事物.因此，对于“鸡兔同笼”问题，可以作出对应的“形”，如图1所示.然后就可以基于图形进行解题，将腿与头相匹配，即将圆形与线段相匹配，注意每一个圆形匹配两条或四条线段.首先，需要保证每个圆形至少都有两条线段进行匹配，所以第一步将所有圆形与两条线段匹配.其次，将剩余线段与圆形匹配.

由此可见，直译法相比于枚举法或列表法，利用“数”与简单的“形”相结合，更直观形象，有助于帮助学生发现问题的限制条件.同时，其解题思路与假设法具有共同之处，而数形结合能帮助学生更好地理解解题思想与解题规律.

2.2 转译法

“鸡兔同笼”是关于数量关系的数学问题，而方程是刻画现实世界中数量关系的一个有效数学模型.因此，也可以通过设未知数的方式，构造方程进行求解.这类方法较为常规，学生也易于理解.

设鸡的数量为x，兔子的数量为y.根据题意可得x+y=35，2x+4y=94.

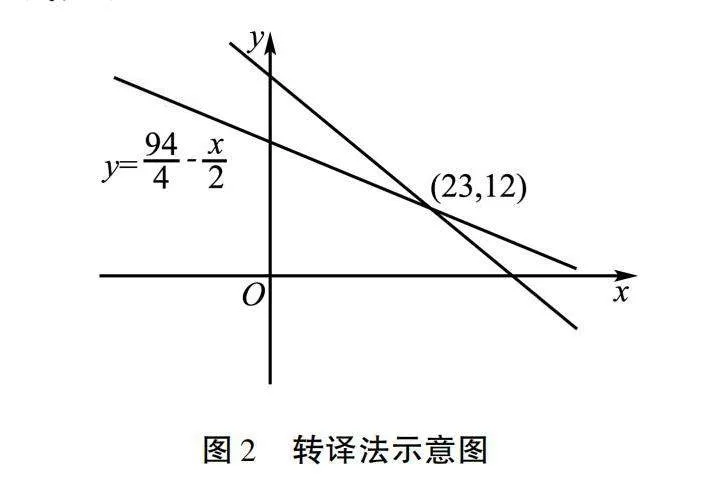
初步分析：可转化为求解方程组y=35-x，y=944-x2.

求解：如图2所示.

两直线的交点坐标即为方程的解，交点的横坐标对应鸡的数量，交点的纵坐标对应兔子的数量.需要注意的是，在将“鸡兔同笼”问题转化为方程求解问题后，其求解方法不止一种，此处仅列举了一种数形结合方法，其他方法不再赘述.

2.3 建模法

在直译法中已经介绍了用图形语言描述“鸡兔同笼”问题的一种思路，该思路是借助学生对实际物体形的认识，直接进行“数”与“形”的结合.但无论是用圆形表示头数，还是用线段表示脚数，“数”与“形”之间的联系并不密切，如圆形可以替换为三角形、方形等，线段的长度没有限制，并同样可用其他形进行直接替代等.“形”与“数”匹配的模糊性较大，“形”中并未很好地体现“数”的关系.基于此，利用建模法为“数”配“形”，最大化地利用“形”，运用数形结合解决“鸡兔同笼”问题.

“鸡兔同笼”问题中涉及了几个数字，直译法中是用几何图形的个数来表示“数”，相对单一，且不具备特殊性，可进一步尝试对线段长度进行限制.用线段长度分别表示鸡和兔子的脚数，用长方形面积表示总脚数，以解决鸡兔同笼问题.

建模：如图3所示，已知AG=35，AB=2，GF=4，求AD，DG的长.

以“数”解“形”：运用割补法，即利用已知的线段长度和图形面积构建相应的等量关系，求得未知线段的长度，从而使问题得到解决.

由此可见，数形结合思想为问题解决提供了新思路.因此，学生需要进行再次审题并分析题干信息，将“数”的信息转化为“形”的信息，为下一步求解奠定基础.建模法中不仅利用“形”的性质对“鸡兔同笼”问题进行转化，更重要的是，通过运用数形结合的解题方法，将复杂的数量关系以直观明了的图形形式呈现出来，形象直观、易于理解.且“数”与“形”之间联系密切，由“数”构造对应的“形”，由“形”得到新的数量关系，最终解决“鸡兔同笼”问题.

3 结束语

在中学数学中，数形结合的主要应用是以几何辅助代数的学习，把“形”作为认识“数”的工具，对数形结合的认识相对单一.然而，数形结合应当既注重将抽象数学概念通过图形具象化的过程，也要关注将具象形状通过代数符号进行处理的过程.这需要依靠“形”来直观理解“数”的概念和关系，也需要将“数”的精确性用于描绘“形”的特征和规律.数形结合在解题中的应用能够有效培养学生的抽象逻辑思维和直觉形象思维，有助于发展学生的抽象能力和创新意识，进一步提高学生分析和解决问题的能力，从而提升学生的数学核心素养.

参考文献：

[1] 张卫星.数形结合让数学学习可视化[J].教学与管理，2020（26）：34-36.

[2] 陈玉娟.数形结合思想贵在“结合”：一类问题错解引发的思考[J].数学通报，2012（10）：38-41，50.

[3] 陶小玉.例谈数形结合思想方法在数学教学中的应用与思考[J].数学教学通讯，2024（3）：72-74.

[4] 王云五.业书集成初编孙子算经及其他三种[M].北京：商务印书馆，1939.

[责任编辑：李 璟]