基于立德树人理念下的“数学分析”教学案例

摘"要：挖掘专业理论知识的思政元素是改变传统数学课程教学的一个亮点，它能给枯燥的理论课堂带来生机、活跃，调动学生的学习兴趣，使学生在学习理论知识的同时树立正确的价值观。本文以“数学分析”中的反常积分概念为例，在课堂教学设计过程中，引导学生以问题驱动的形式思考和分析问题，融入思政元素，将知识点与辩证思想联系起来，提高学生分析问题和解决问题的能力，逐步培养学生理论联系实际的能力。

关键词：数学分析；立德树人；反常积分；教学反思

中图分类号：O17

The"Teaching"Case"of"Mathematical"Analysis"Based"on"the"Idea"of

Foster"Virtue"Through"Education

—Take"The"Concept"of"Improper"Integral"as"an"Example

Lin"Wenxian

Collegenbsp;of"Mathematics"andStatistics，Hanshan"Normal"University"GuangdongChaozhou"521041

Abstract：Exploring"the"ideological"and"political"elements"of"professional"theoretical"knowledge"is"a"bright"spot"to"change"the"traditional"mathematics"teaching，which"can"bring"vitality"and"activity"to"the"boring"theory"class"and"arouse"students'"interest"in"learning"and"enable"students"to"establish"correct"values"while"learning"theoretical"knowledge.Taking"the"concept"of"improper"integral"in"Mathematical"Analysis"as"an"example，this"paper"guides"students"to"think"and"analyze"problems"in"a"problemdriven"way，integrates"ideological"and"political"elements，connects"knowledge"points"with"dialectical"thought，improves"students'"ability"to"analyze"and"solve"problems，and"gradually"trains"students'"ability"to"combine"theory"with"practice"in"the"process"of"classroom"teaching"design.

Keywords：Mathematics"Analysis；foster"virtue"through"education；improper"integral；reflection"on"teaching

2016年，全国高校思想政治工作会议上强调，“要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人”“要用好课堂教学这个主渠道”“所有课堂都有育人功能，不能把思想政治工作只当作政治理论课的事，其他各门课都要守好一段渠、种好责任田”，提出了“各类课程与思想政治理论课同向同行，形成协同效应”的要求。

然而，在现实的教学过程中，思政课本身仍大量存在只把思想政治工作作为课程教学的附属品的现象，思想政治教育的功能没能得到充分的发挥，其他各类课程，尤其是自然科学领域的课程，在实施思想政治教育方面的作用就显得捉襟见肘。要真正落实“各类课程与思想政治理论课同向同行，形成协同效应”，需要广大教师、不同学科加大力度挖掘教学内容的思政教育功能，研究教学方法，精心进行教学设计，才能实现立德树人的目标。

“数学分析”是现代数学的基础，也是现代科学技术中应用最广泛的学科，它是大学本科数学与应用数学专业学生必修的最重要的基础课程，数学分析以学习时间长（三个学期）、知识抽象、逻辑性强为主要特征，它对于学生良好的数学素养的形成以及后续课程的学习起着至关重要的作用。因而，在传授知识的同时，如何将“课程思政”融入数学分析这一抽象理论课程的教学环节之中，是摆在我们面前的难题。本文将以反常积分概念为案例，在教学内容的设计中进行一些探索，以期达到抛砖引玉的作用。

1"教学设计

1.1"教学背景

本节课是学生学习了定积分内容后，具有了一定的积分理论基础。定积分的概念实际上有两个根本的制约：有限的积分区间和有界的可积函数，但在好多现实情况中，这两个局限常常必须突破，就是要讨论非有限区间上的“积分”，或非有界函数的“积分”。这是定积分概念的进一步推广，反常积分概念有着很丰富的实际意义，它在应用数学领域中起着特别重要的作用，是一元函数积分学的重要组成部分。

1.2"教学目标

1.2.1"知识目标

理解无穷限反常积分和无界函数反常积分的概念，并掌握计算。

1.2.2"能力目标

通过本节课的学习，学生要进一步认识极限与积分的关系，培养学生的化归、类比和分析等数学思想，提高分析与解决实际问题的能力。

1.2.3"思政目标

将“思政元素”融入专业课堂，通过积分区间无穷而积分存在以及被积函数无界而积分存在的矛盾关系，培养学生认识主次矛盾的辩证关系，使学生建立良好的人生观、价值观、世界观。

1.3"教学重点

两类反常积分的概念与计算。

1.4"教学难点

诱导学生理解反常积分的数学思想方法的形成过程。

1.5"教学方法

问题驱动教学法，讲授法。

1.6"教学过程

1.6.1"问题引入

首先，简单介绍我国在航空领域取得的伟大成就，跻身世界航天大国，让学生油然而生民族自豪感。然后播放我国首次探测火星的“天问一号”火箭发射升空的视频（图1），引导学生的科技探索精神，激发学生爱国热情和学习兴趣，并提出问题：要使“天问一号”发射升空，奔向火星，发射火箭的初始速度应为多少？这在物理学上称为什么速度？如何求出来？

这样就引出了计算第二宇宙速度的问题，并给出以下例题。

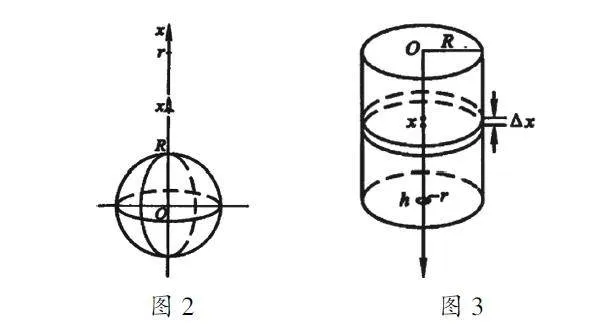
例1：（第二宇宙速度问题）在地面垂直发射火箭，为使火箭能摆脱地球引力无限远离地球，试问至少需要多大的初速度v0？（如图2）

例2：圆柱形桶的内壁高为h，内半径为R，桶底有一半径为r的小孔。试问从盛满水开始打开小孔直至流完桶中的水，共需多少时间？（如图3）

通过这两个例题讲解让学生发现，在例1求第二宇宙速度可以转化为求一个积分下限为R，上限为正无穷大的积分，即积分区间为［R，+∞），这与以前学习的定积分不一样，这种积分称为“无穷限反常积分”；在例2求圆桶水流完所需时间问题可以转化为求一个被积函数是有界函数的积分，这也与以前学习的定积分不一样，这种积分称为“无界函数反常积分”。

同时，提出问题：如何研究这两类积分？

1.6.2"反常积分的定义

定义1：设函数f定义在无限区间［a，+∞）上，且在任意有限区间［a，u］上可积，若极限limu→+∞∫uaf（x）dx=J存在，则称函数f在［a，+∞）上的无穷限反常积分（简称无穷积分）为此极限J，记作J=∫+∞af（x）dx，并称∫+∞af（x）dx收敛。若极限不存在，就称∫+∞af（x）dx发散。

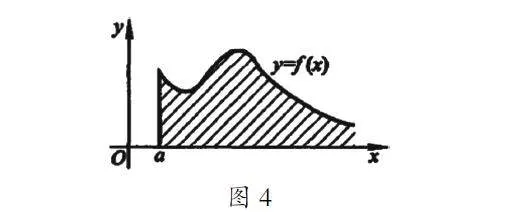
注：∫+∞af（x）dx收敛的几何意义是：如果f定义在［a，+∞）上的连续非负函数，则如图4所示，位于直线x=a，x轴和曲线y=f（x）之间那一向右无穷延长的阴影部分有面积J。

定义2：设函数f定义在（a，b］上，在点a的任一右邻域内无界，但在任何内闭区间［u，b］（a，b］上有界且可积，如果存在limu→a+∫buf（x）dx=J则称此极限为无界函数f在（a，b］上的反常积分（简称瑕积分），记为J=∫baf（x）dx并称反常积分∫baf（x）dx收敛，若极限不存在，则称反常积分∫baf（x）dx发散。

1.6.3"例题讲解

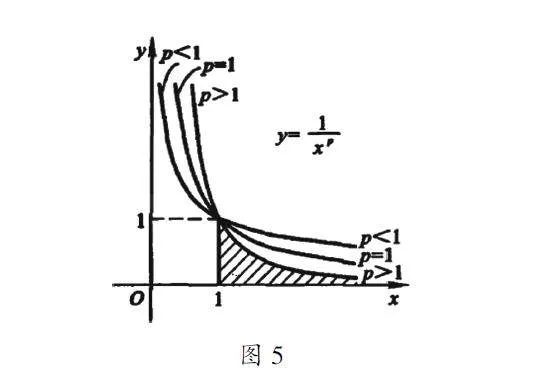
例3：研究无穷积分∫+∞11xpdx的收敛性。

例4：研究下面积分的收敛性。

例5：（1）∫+∞21x（lnx）pdx；（2）∫+∞-∞11+x2dx。

例6：研究积分∫+∞acosxdx的收敛性。

例7：判定积分∫1011-x2dx的收敛性。

例8：研究无界函数反常积分∫101xqdx（q＞0）的收敛性，并考虑积分∫+∞01xqdx的收敛性。

1.6.4"无界函数反常积分与无穷限反常积分的联系

设函数f（x）连续，b为瑕点。令t=1b-x，有∫baf（x）dx="∫+∞1b-afb-1t·1t2dt。则将无穷限反常积分化为无界函数反常积分。

又设a＞0，令t=1x，有无界函数反常瑕积分化为无穷限反常积分，于是，无界函数反常瑕积分与无穷限反常积分可以能够互相转化。所以，它们有相似的理论和结果。

1.7"知识小结

无穷积分和瑕积分实际上转化看作变限积分函数的极限。

2"教学反思

2.1"思政元素

通过介绍我国航天领域的发展史，让学生增强民族自豪感，学习我国航天科技工作者艰苦奋斗、勇于探索、开拓创新的精神。同时，通过讲授无界函数反常积分与无穷限反常积分的关系，让学生体会到，它们的关系表现了对立统一规律，又称矛盾规律、对立统一规律和斗争规律，它表明了矛盾存在于任何领域中，也存在于任何事物、事物内部和事物之间。从而引导学生的认识上升到哲学的高度，用辩证的思维方式去理解具体领域具体学科的知识，帮助学生认识到整个世界是充满矛盾的，矛盾无时不有、无处不在，正是矛盾双方的对立统一，推动着事物的运动、变化和发展，以更自觉地掌握矛盾观点，并学会用矛盾的观点去认识世界，用矛盾分析的方法去指导改造世界。

2.2"教学思考

利用创设合适的问题情境，引入新课内容，以避免学生对内容的突兀感。通过观看“天问一号”发射视频引出计算第二宇宙速度问题，进而得出无穷限反常积分的概念。通过求解流水问题，得出无界函数反常积分的概念。

一元函数积分学作为数学分析的重要组成部分之一，可以分成定积分和反常积分两大类，反常积分又包括无穷限反常积分与无界函数反常积分，它们都是定积分的推广，是定积分的变限积分的极限形式，本质上是某类函数的极限。因而在反常积分的学习过程中，应该关注反常积分与定积分的一些性质有所相同，也有所不同。

注意运用几何图像的直观性，特别是对反常积分几何意义的讲解，帮助学生理解抽象的数学概念，特别是注意文字语言、符号语言和图形语言的相互转换。

结语

在立德树人理念下，数学专业教师要把“德育”看作是教育的根本任务，更新观念，深入挖掘，以数学学科知识为载体，发挥数学育人的特殊作用，促进学生树立正确的世界观、人生观和价值观。在高等学校专业基础课中，教师如何渗透课程思政？如何发现每个知识点的思政元素？如何提高学生学习知识的积极性？这是高校教师面临的一个课题，任重而道远，是一个值得深入思考和研究的终身课题。

参考文献：

［1］华东师范大学数学科学学院.数学分析（上册）［M］.北京：高等教育出版社，2019.

［2］林文贤.反例在数学分析教学中的作用［J］.高师理科学刊，2008，28（4）：9395.

［3］钟煜妮，林文贤.分部积分法在重积分的应用［J］.高师理科学刊，2015，35（1）：11.

［4］林文贤.高师数学分析课程对学生数学素质的培养［J］.韩山师范学院学报，2005（3）：9295.

［5］林文贤.“三全育人”理念下《数学分析》教学案例——以《条件极值》为例［J］.科技风，2024（1）：2123.

基金项目：广东省一流课程《数学分析》建设项目（Z21011）；2021年度韩山师范学院教育教学改革项目（52"1104）；2022年度韩山师范学院质量工程建设项目（E22033）

作者简介：林文贤（1966—"），男，广东潮州人，教授，从事数学分析的教学与研究。