有意义的数学问题：提升主题活动内驱力

【摘" "要】有意义的数学问题是设计主题活动的核心和推动学生深入思考的关键。教师聚焦驱动性问题“一个物体的容积可能大于它的体积吗？”，设计了“猜想、验证、评价、反思、拓展”的活动内容，并在实施过程中为每个任务匹配核心问题，引导学生经历探索的全过程，体会数学与生活之间的联系，积累基本活动经验，感悟数学思想，发展核心素养。

【关键词】数学问题；主题活动；体积和容积

一、主题活动背景

长方体是小学数学五年级下册的内容，教学这一内容旨在引导学生从度量的角度认识长方体，并掌握其要素与特征。在学习这一内容的过程中，学生需积累认识与探究立体图形的基本经验，从而发展空间观念和推理意识。由此，学生对立体图形的认知由感性走向理性，实现从定性描述到定量刻画的转变。

在学生学完长方体的体积与容积的相关内容后，笔者针对“一个物体的体积一定大于它的容积吗？”这一问题，对他们进行了后测。结果显示，约93%的学生认同此结论，他们仅基于体积与容积的基本概念，认为由于物体具有厚度，故其容积自然小于体积。仅有7%的学生对此结论提出质疑，但未能给出充分的理由。这一现象表明，五年级学生虽然已具备研究立体图形的基本活动经验，但在知识应用层面仍存在不足。产生这一现象的原因主要有两方面。一方面，现行教材中对体积与容积关系的阐述较为匮乏，未能有效帮助学生建立两者之间的紧密关联，从而影响了他们对三维度量的整体认知。另一方面，由于缺少生活应用价值的引导，学生难以将所学知识与实际情境结合起来，更无法明确这些知识在实际生活中的应用场景。

《义务教育数学课程标准（2022年版）》指出，主题活动分为融入数学知识学习的主题活动和运用数学知识及其他学科知识的主题活动两类。针对学生在体积与容积关系理解上的不足，在长方体知识复习阶段，笔者尝试借助第二类主题活动来突破这一难点。即让学生面对生活背景，从数学的角度发现并提出值得探究的问题：“一个物体的容积可能大于它的体积吗？”引导他们综合运用体积、容积等的知识与方法，积累提出猜想、规划步骤等经验，并内化类比、转化等数学思想方法，以分析和解决相关问题。

二、主题活动设计

提出有意义的数学问题是推动学生深入思考的关键。本次主题活动聚焦驱动性问题“一个物体的容积可能大于它的体积吗？”，从确立活动目标和构建进阶任务两个方面进行设计。

（一）确立活动目标

立体图形的认识与测量之间有着密切的联系。本主题旨在引导学生在实际情境中，综合应用长方体的特征、体积、容积等知识点，通过提出猜想和设计实验方案，探究物体体积与容积之间的关系。然后分析不同实验方法，反思体积与容积的关系，积累研究立体图形度量属性的基本方法，并深入感悟转化等数学思想方法。接着通过改造立体图形，改变其底面积或高，归纳影响体积与容积关系的关键要素。最后，通过找出或创造容积大于体积的物体，使学生形成初步的推理意识、应用意识和创新意识，并进一步发展其空间观念。

（二）构建进阶任务

进阶任务为主题活动的有序开展提供了支架。笔者围绕驱动性问题，对研究任务进行分解（如表1），使学生对概念的理解从定性的描述逐步向定量的刻画转变。然后在定量刻画时，形成多样的研究方法，内化容积与体积间的关系。

三、主题活动实施

主题活动的实施要注重关联性。一是过程的关联，例如，在第1课时中，教师要引导学生提出猜想，并设计研究方案，验证猜想。在第2课时中，教师要在课前收集学生的实践成果，选择适切的作品作为课中评价与反思的学习材料。二是思维的关联，教师要不断引导学生回顾与反思：体积与容积有关系吗？如果有，是什么关系？怎么来说明体积和容积的关系？还有别的方法可以说明吗？

（一）第1课时：猜与做

1.项目启动，回顾概念

在探究体积与容积之间的关系之前，先让学生回顾对体积和容积的认识。

2.聚焦关系，提出猜想

● 核心问题1：你们觉得一个物体的体积与它的容积之间有怎样的关系？

部分学生认为体积和容积是有关系的，并推测体积肯定比容积要大，理由是容积是从物体内部测量的，物体本身的厚度导致其内部空间小于外部尺寸。也有部分学生认为体积和容积是两个不同的概念，无法直接进行比较。

教师呈现课前调查结果：有40名同学认同“一个物体的体积一定大于它的容积”的观点，但仍有3名同学对此表示质疑。

3.讨论材料，选定方法

● 核心问题2：你们打算怎么来验证自己的猜想？

在讨论问题的过程中，学生提出需根据物体形状进行分类讨论。对于不规则物体，可以采用“排水法”进行研究；而对于规则物体（如长方体），则可以利用底面积乘高、比较两个长方体的体积差等方法来探究体积与容积的关系。

4.合作研究，探究关系

明确任务：两人合作，选择材料，利用计算、实验等方法来验证猜想。

（实施建议：本环节的关键在于设计研究方案。在实施过程中，教师可提供如表2所示的方案设计的基本框架，帮助学生系统地规划研究过程。）

（二）第2课时：评与思

1.材料收集，成果赏析

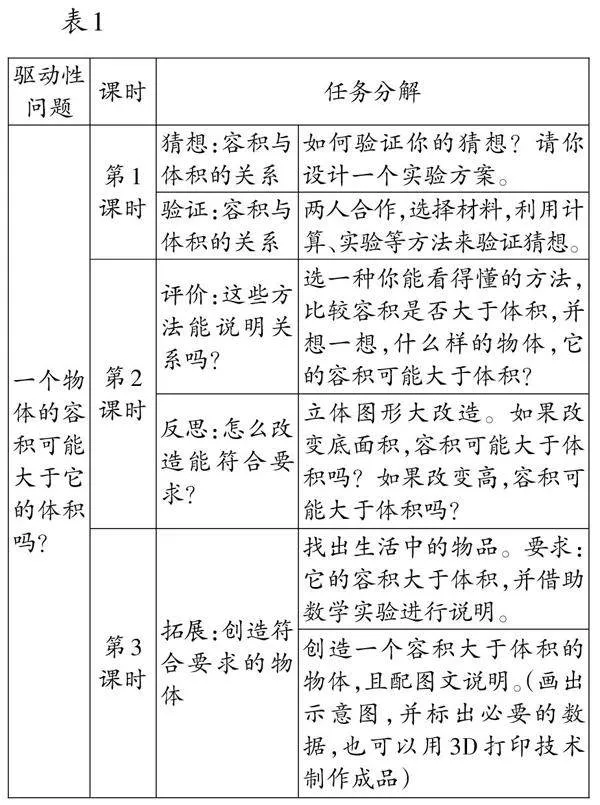
为了让学生更深入地理解一个物体的体积与它的容积之间的关系，教师组织学生以小组为单位进行探究，并收集了3个小组的研究成果（如图1），以供全班共同学习。

2.明确要求，团队合作

（1）选：四人小组合作，每个小组至少选择一个作品进行研究。

（2）比：比较同一物体的体积与容积的大小关系。

（3）想：什么样的物体，它的容积可能大于体积？

3.项目评估，关系理解

（1）立体图形的体积与容积——数出体积单位的个数

● 核心问题3：怎么求出无盖立体物体的体积？

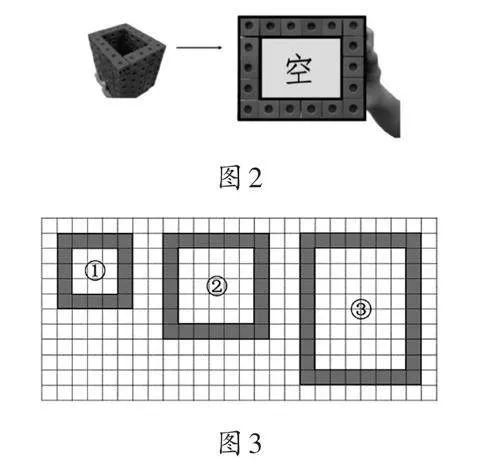
学生通过计算发现：作品2中，水杯的容积是（7-2）×（7-2）×（10-1）=225（立方厘米），V体=V总-V容=7×7×10-225=265（立方厘米）。所以，这个立体图形的体积大于它的容积。教师顺势引导学生提出疑问：算容积的时候，为什么长、宽要分别减2，高要减1呢？学生用联系的眼光进行分析：先回顾作品1中搭积木的过程，之后进行想象，如果用棱长是1厘米的小立方体摆出水杯的形状，底下这层摆满，上面的每一层都摆成“回字形”，一共要摆10层。因为杯子有厚度，所以在计算容积时，长、宽要分别减去2个1厘米，高要减去1个1厘米。之后，引导学生验证作品1中立体图形体积与容积之间的关系。

（2）烧杯的体积与容积——从不规则物体到规则物体的转换

针对学生对作品3的研究过程与结论进行解读。在两个相同容器中注入等高的水，先将烧杯完全浸没在容器①中，此时水位上升的体积就是烧杯的体积。再在烧杯中加满水，将水倒入容器②中，此时水位上升的体积则为烧杯的容积。由于容器②的水面高于容器①，因此烧杯的容积大于它的体积。总的来说，无论是体积还是容积，都是通过将不规则物体转换为规则物体进行测量的。

4.对比反思，提炼要素

教师引导学生思考：什么样的物体，它的容积可能大于体积？

学生认识到，如果是封闭物体，它的体积一定大于容积；如果是不封闭的物体，在厚度较小（壁较薄）的情况下，它的容积可能大于体积。

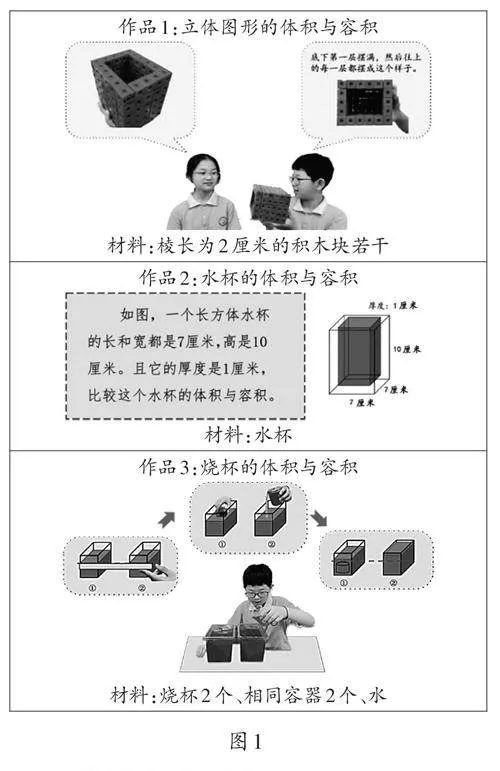
● 核心问题4：如图2所示的物体，如果继续往上搭小立方体，它的容积可能大于体积吗？选择图3中哪个形状作为底面，构造的物体的容积可能大于体积？

● 核心问题5：高为多少时，物体的容积可能大于它的体积？

教师出示任务：图3中的②号图形即为之前作品2中的水杯的“横截面”。若按照上述规律，用1立方厘米的立方体继续堆砌水杯，当水杯的高度达到多少厘米时，它的容积会大于体积？（尝试以他人看得懂的方式表述你的思路，如列式、画图、列表等）

（实施建议：在学习材料的选择上，应强调度量的本质属性。前两个作品中的物体都可以直接数出体积单位的个数，而作品3涉及不规则物体，须转换为规则物体进行测量。由此，加深学生对体积与容积概念的理解。）

（三）第3课时：课外拓展，创意制造

让学生选择一个任务完成：（1）在生活中找出容积大于体积的物体，并利用数学实验进行解释。（2）创造一个容积大于体积的物体（可附上示意图，标注必要数据，也可采用3D打印技术制作实物）。

（实施建议：在评价过程中，无论是对找出还是创造符合要求的物体，重点都应放在验证方法和说明理由上。可借助如表3所示的评价量规，统计各水平层次的学生人数，并组织学生交流分享他们的成果。）

总而言之，提出一个有意义的数学问题比解决问题更重要。有意义的数学问题能为学生带来认知冲突，具备实践价值。本主题活动围绕一个有意义的数学问题，设计了“猜想、验证、评价、反思、拓展”的活动内容，并在实施过程中为每个任务匹配了核心问题，形成了驱动性问题、任务设计、核心问题的三级实施路径。其目的在于引导学生经历探索的全过程，体会数学与生活之间的联系，积累基本活动经验，感悟数学思想，发展核心素养。