承续已有知识，促进算理迁移

【摘" "要】聚焦“计数单位的细分”这一概念，研究团队探索并优化了一条基于算理一致性的“除数是整十数的除法”的学习路径，引导学生：通过承续已有知识，感受除数是一位数的除法中计数单位的细分；借助类比迁移，体会除数是整十数的除法与除数是一位数的除法算理上的一致性；依托巩固训练，强化对计数单位细分及算理一致性的理解。该学习路径突出计数单位细分对整数除法的作用，促进学生学会迁移。

【关键词】除法；计数单位；单位细分；学习路径

一、问题提出

《义务教育数学课程标准（2022年版）》明确指出：数的运算重点在于理解算理、掌握算法。学生经历算理和算法的探索过程，体会数的运算本质上的一致性，有助于其形成运算能力和推理意识。除数是两位数的除法是小学阶段整数除法学习的最后阶段，也为小数除法的学习奠定基础，在除法学习中起着承上启下的作用。然而，在现行教材的教学中，教师尚未贯通“除数是一位数的除法”“除数是整十数的除法”以及“除数是整百数的除法”的算理，学生也并未体会到三者在本质上均是对计数单位的细分，导致知识的整体性被破坏［1］。尽管已有研究尝试从计数单位的角度解释除数是一位数的除法的算理［2］，但仍未打破“除数是一位数的除法”“除数是整十数的除法”与“除数是整百数的除法”三种除法之间的壁垒，实现算理的一致性。因此，如何基于现有教材，通过优化设计学习路径来贯通“除数是一位数的除法”“除数是整十数的除法”与“除数是整百数的除法”算理的一致性，促进学生实现高通路迁移，是目前亟待解决的问题。

本研究将聚焦“计数单位的细分”这一概念，从“除数是一位数的除法”出发，借助学生已有的知识经验，探索一条基于算理一致性且学生易于理解的“除数是整十数的除法”的学习路径，以此实现“除数是一位数的除法”“除数是整十数的除法”与“除数是整百数的除法”在算理上的一致性。研究主要围绕以下两个子问题展开。（1）如何通过除法的意义（平均分）来理解除数是一位数的除法的算理实际上是“计数单位的细分”？（2）如何设计有效的学习迁移路径，将除数是一位数的除法的算理迁移至除数是整十数、整百数的除法中，从而使学生能够深刻感受到算理的一致性？

基于此，笔者选取杭州市YHSY小学四年级的两个平行班（分别记为甲班和乙班）共58名学生作为研究对象，按照研究设计的学习路径进行教学。通过比较两个班级学生的学习情况，检验优化后的学习路径的教学效果。学习路径优化的具体流程如图1所示。

二、路径优化

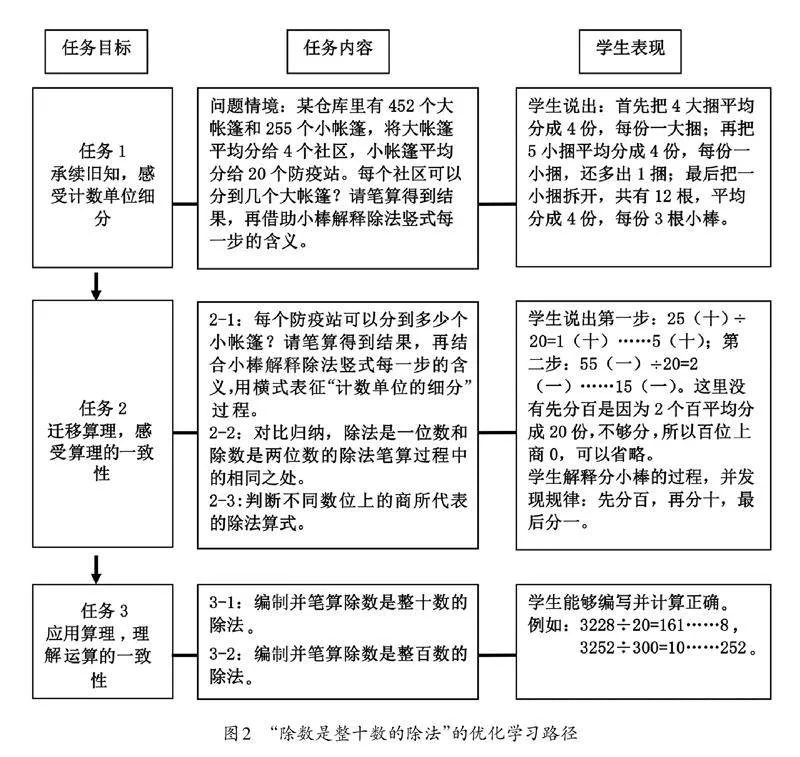
根据学习路径的优化流程，结合“除数是整十数的除法”的教学内容构建如图2所示的优化学习路径。

（一）复习旧知，感受算理，解决难点，体会除数是一位数的除法就是计数单位的细分

教师以“分帐篷”为问题情境，引导学生通过笔算回顾三年级学过的除数是一位数的除法，解释452÷4的算法。这一任务旨在唤醒学生已有的算法经验，为学生解释笔算过程提供支架。三年级学生对除法的意义——平均分，已经有了较深入的理解，但在本节课中，由于平均分的对象是计数单位，其抽象性增加了学生理解上的难度。因此，教师在教学过程中需要引导学生结合具体情境来解释竖式计算过程，帮助学生初步理解用横式表达竖式中平均分的过程。

【教学片段1】

师：谁能来说说竖式452÷4（如图3）每一步分别表示什么意思？

生：第一步是将400个帐篷平均分给4个社区，每个社区分到100个帐篷。

师：400个帐篷也可以看成4个几除以4？

生：4个百。

师：用算式表示的话就是——

生：4个百除以4。

师：它的结果表示什么？

生：每个社区分到1个百。

（师生合作板书，一步步解释完整的计数单位细分过程，如图4）

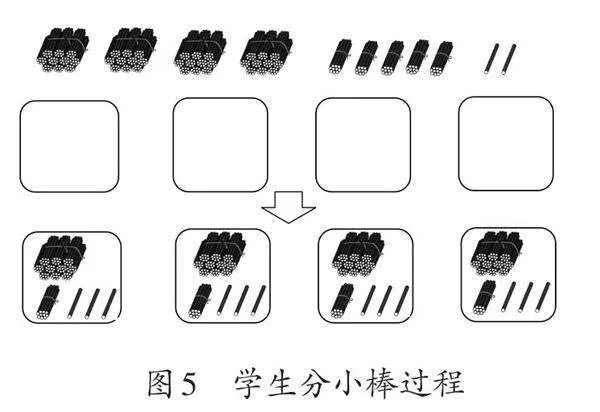
随后，教师引导学生思考“先分什么，后分什么”，并要求学生将大捆、小捆和几根小棒平均分到4个框中（如图5）。教师再次总结，将直观分小棒图的过程与横式联系起来，强化学生对计数单位细分的理解。

综上所述，通过任务1，学生利用数形结合的方式，对除法意义的理解从平均分过渡到计数单位的细分，逐步感受到除数是一位数的除法的算理是计数单位的细分。

（二）迁移算理，学习新知，聚焦重点，从除数是一位数走向除数是整十数

在任务2-1中，教师首先鼓励学生尝试笔算255÷20，随后要求学生参照除数是一位数的除法的笔算过程，通过物体的均分初步判断他们笔算过程的正确性，从而增强对计数单位细分过程的理解。考虑到算理理解的难度，教师应引导学生类比除数是一位数的除法分小棒图的过程，再次运用小棒图解释除数是整十数的除法笔算过程每一步的含义，思考先分什么小棒，对应分什么单位，从而建立起小棒、横式和竖式之间的联系，进一步加深学生对算理的理解。

【教学片段2】

师：我看到有好几个同学是这样写的（如图6），你们看懂了吗？

生：25个十平均分成20份，每份可以分到1个十，还余5个十。

师：下一步他在分什么呢？

生：他在分55个一，因为前一次细分还剩50个帐篷，再加上还没分的5个帐篷，一共有55个帐篷没有分。将这55个帐篷平均分给20个防疫站，每个防疫站能分到2个帐篷，还剩下15个帐篷。

师：先分25个十，平均分成20份，每份可以分到1个十，还余5个十。接着，将5个十拆分为50个一，和5个一合起来是55个一。然后，将55个一平均分成20份，每份分到2个一，还剩下15个一。

师：我们也可以通过分小棒的方法来梳理255÷20的计算过程。

生：先分2大捆，平均每份0大捆，还余2大捆。

师：这2大捆就是2个百，它们该怎么分呢？

生：把这2大捆拆成20个小捆，共有25个小捆，每份分到1小捆，还剩下5小捆。

师：这25个小捆就是25个十，那剩下来的5个十又该怎么分呢？

生：再拆，拆成50个一，共55个一，也就是55根小棒。

（教师板书，将横式与分小棒的过程一一对应，如图7所示）

接下来，教师引导学生比较笔算255÷20与452÷4计数单位细分的过程（如图8），以完善学生对从最高位开始细分计数单位的理解，从而明白无论除数是一位数还是整十数的除法，都是从最高位开始细分计数单位的。

【教学片段3】

师：同学们，我们在解决255÷20这个问题时，是不是借鉴原来452÷4的经验？请你们观察一下左右两边的板书（如图8），你有什么发现？它们有什么相同的地方？

生：它们都是从最多的那个开始分的。

师：最多是什么意思？

生：都是先分大捆，再分小捆，最后分根。

师：你们所说的大捆其实就是1个百，小捆就是1个十，小根就是1个一。

师：这是我们数学里原来学过的什么？

生：计数单位。

师：那么，我们刚刚从大到小分小棒的过程，其实也是一步步分计数单位的过程，而像这样分的过程就叫作计数单位的细分。

由此，从除数是一位数的除法过渡到除数是整十数的除法，对算理进行了总结，但学生在算理的理解上仍然存在困难。因此，教师需要通过布置两道选择题（如图9），引导学生辨析竖式中的横式，并布置相应的计算题来巩固学生对算理的理解，为他们在后续学习中应用算理奠定基础。

综上所述，通过任务2的层层推进，学生首先从算法入手，初步感受计数单位细分在竖式中的应用；然后转向横式，对算理有初步的理解；最后通过摆小棒，与横式、竖式互译，巩固对计数单位细分的理解，从而加深对算理的理解。接下来，任务3将帮助学生应用算理提升运算能力，并通过变式练习来完善对算理的理解。

（三）拓展应用，实现贯通，打通堵点，从除数是整十数走向除数是整百数

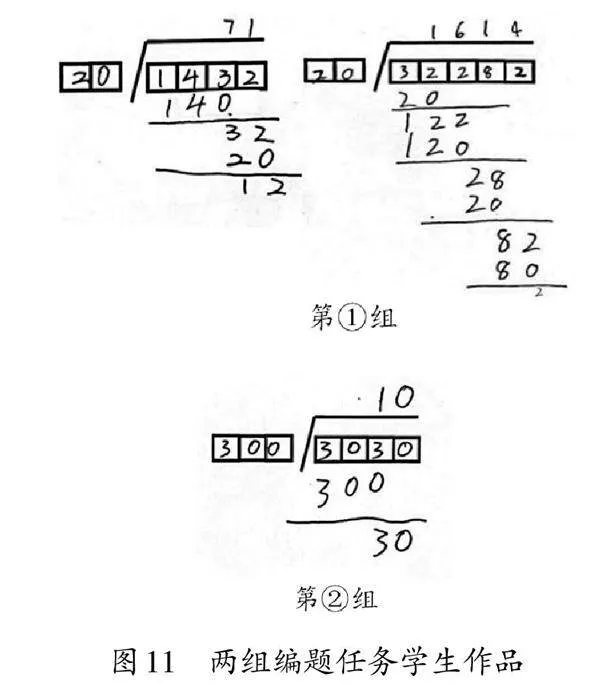
为了加深学生对算理的理解，教师设计了任务3-1。在这一任务中，学生将面对除数是整十数，被除数是四位数和五位数的除法问题（如图10）。教师先向学生介绍编题的要求，即先编一编，再算一算，待学生完成后，随机抽取学生解释计算每一步的含义。通过这样的练习，学生不仅能够应用除法算理进行计算，还能提升除法的运算能力。

随着学生对算理的进一步巩固，教师设计了任务3-2，以强化学生对算理一致性的认识。在这一任务中，学生将类比除数是一位数以及两位数除法的学习经验，自主探究并笔算除数是整百数的除法（如图11第②组），促进学生在计算过程中再次感受算理的一致性。最后，教师引导学生观察这两组编题的计算过程（如图11），并总结升华整数除法的算理。通过这一系列的练习，学生将深刻理解到无论除数是一位数、整十数还是整百数，其除法算理都是对计数单位的细分，从而帮助学生全面理解各种除法算理的一致性。

综上所述，学生通过除数是一位数的除法，唤醒了算法上的经验，初步体验了计数单位的细分过程；随后通过迁移新知，感受到除数是整十数的除法在算理上的一致性；最终通过巩固训练，强化了对计数单位细分及算理一致性的理解。

三、效果检验

为了检验优化后的学习路径的实施效果，本研究设计了三种类型的后测题，共包括七个具体问题，以检测学生对算理一致性的理解水平［4］。后测问卷的Cronbach's α系数为0.93，显示出较高的信度。后测主要从“算理理解、算理迁移、创新应用”三水平进行检测。各水平任务评分标准如下：学生能正确回答被除数由哪些计数单位构成，说明达到“算理理解”水平，得1分，回答错误或者没有回答计0分，共2题。学生能使用横式记录笔算过程，并得出正确结果，说明达到“算理迁移”水平，得2分，仅能列出横式或采用包含除计算正确结果计1分，计算错误或未作答计0分，共1题。学生能将除数是整十除法的算理迁移至除数是非整十数的除法，使用横式记录笔算过程，并得出正确结果，说明达到“创新应用”水平，得2分，仅列出竖式计1分，计算错误或未作答计0分，共4题。

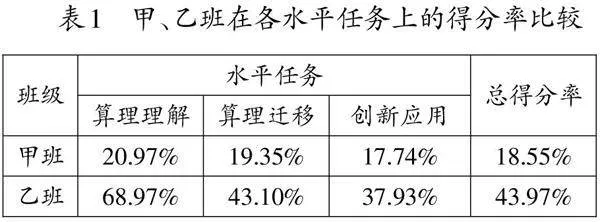
基于此，对甲、乙两个班学生的后测数据进行定量分析，得出他们在各水平任务上的平均得分情况（如表1）。后测结果显示，乙班学生在三个水平上的得分率均高于甲班学生，且在“算理理解”的表现上，两个班的学生之间存在显著差异。

乙班学生的问卷答题情况如表2所示。从表中可以看出，学生不仅能够理解算理，还能清晰地表述除数是整十数的除法计数单位细分的过程（如25号学生）。同时能够根据算理的一致性，在计算除数是整百数的除法的过程中一步步细分计数单位（如1号学生）。此外，还有学生能迁移估算算法，结合除数是整十数的除法和除数是非整十数的除法算理的一致性，清晰地解释除数是非整十数的除法的计算过程（如13号学生）。

综上所述，优化后的学习路径A2在帮助学生理解除数是整十数的除法的算理、迁移算理，以及感受整数除法算理的一致性方面表现出显著的效果。

参考文献：

［1］马云鹏.深度学习的理解与实践模式：以小学数学学科为例［J］.课程·教材·教法，2017，37（4）：60-67.

［2］章颖.依惑而教：从物的等分到计数单位的等分：“两位数除以一位数”笔算教学的思考与实践［J］.教学月刊·小学版（数学），2023（12）：57-60.

［3］喻平.《义务教育数学课程标准（2022年版）》学业质量解读及教学思考［J］.课程·教材·教法，2023，43（1）：123-130.

*本文系浙江省哲学社会科学规划课题“基于认知发展模型的义务教育教科书编写质量提升研究”（课题编号：23NDJC265YB）、浙江省高校重大人文社科攻关计划项目“建设高质量教育体系背景下义务教育教科书编写质量提升路径研究”（项目编号：2023GH005）的研究成果。巩子坤为本文通讯作者。