聚焦量率意义 统整数的认识

【摘" "要】在情境中，整数、小数和分数都具有数量和关系两层意义。在实际教学中，可以尝试在教学“倍的认识”时就提前孕伏量率意义，从“整数倍”开始，为不同数系的数均能表示量率意义奠定基础。教师以人教版教材“倍的认识”为例，通过“分析教学内容，提炼核心概念；精准把握学情，确立学习起点；设置核心任务，构建量率意义”等探索与实践，实现整体性的关联和阶段性的渗透，确保教学的全面性和深度。

【关键词】量率意义；倍的认识；数的认识

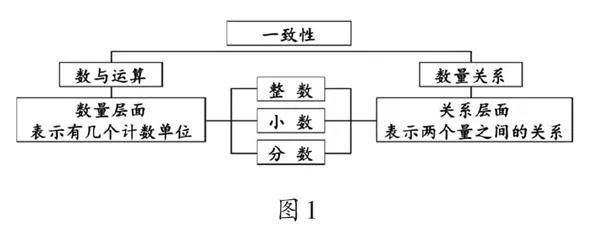
在“倍的认识”的教学中，教师往往将“倍”与前概念“几个几”或“份”相联系，着重分析倍数关系的结构和模型的建构。量率意义的渗透主要依托“分数”教学，从分数表示一个量开始，逐步扩展到分数表示两个量的关系，从而凸显分数的量率意义。然而在情境中，整数、小数和分数都具有数量和关系两层意义。从一致性的视角审视，在数量层面，无论是整数、小数还是分数，它们都表示有几个计数单位；在关系层面，这些数都能表示两个量之间的关系（如图1）。

基于此，可否尝试在教学“倍的认识”时，就提前孕伏数的量率意义，从“整数倍”开始，为不同数系的数均能表示量率意义奠定基础？下面以人教版教材“倍的认识”为例进行深入探究与实践。

一、分析教学内容，提炼核心概念

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）将“数与代数”领域划分为“数与运算”和“数量关系”两个主题。将“数量关系”专门设为一个学习主题，为“数与代数”领域增设了新的研究视角。

在现行教材中，相差关系编排在一年级下册“20以内的退位减法”单元中，倍数关系编排在三年级上册“倍的认识”单元中。这两个单元均通过解决问题的形式进行编排，虽强调了数量关系的分析，但并未深入探讨一个数从“表示具体数量”到“表示数量之间关系”的转变。仅仅是在整数教学中强调数量意义，在分数教学中强调关系意义。

自2022年版课标颁布以来，为了凸显教学的一致性，教学中基本采用计数单位作为大概念来连接整数与分数。但从本质上讲，这种关联仍然基于数量意义。事实上，在当前教学中，很少会从数量之间关系的角度来连接整数、小数和分数。

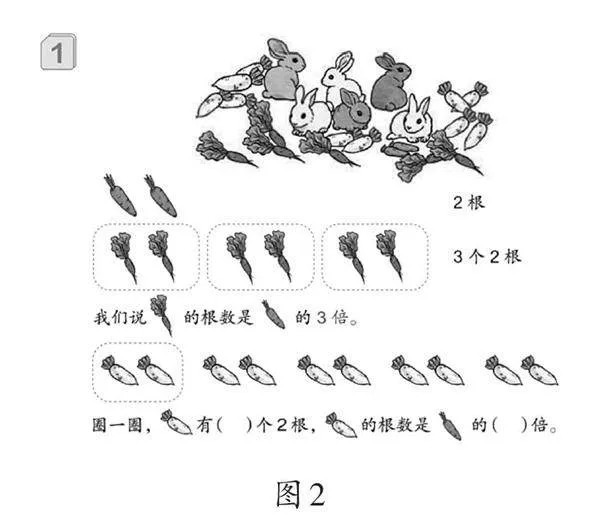
小学阶段涉及两个基本的数量关系模型，即加法模型“总量=分量+分量”和乘法模型“总量=每份量×份数”。对于作为学习比率起点的“倍的认识”，现行教材的编写有诸多值得商榷的地方（如图2）。首先，例题素材采用多样化的萝卜，对缺乏生活经验的学生而言，要准确辨认这些萝卜并不容易。这导致学生在表述倍数关系时不知如何表示各种萝卜，因而说不清谁是谁的几倍。其次，教材中缺乏核心任务的明确表述，学习目的模糊，难以识别。最后，对倍数关系中至关重要的“标准量”，教材中也未进行明确标注（如圈画）或强调，这不利于倍数模型的建构。由此可见，教学“倍的认识”时应关注关系本身，精心选择素材和设计任务，以促进学生深度理解和构建相关概念。

二、精准把握学情，确立学习起点

学生能否在“倍的认识”的学习中初步感悟整数的量率双层意义，且具体地描述两者的区别？为探讨这一问题，笔者围绕整数表示数量、相差关系、倍数关系三方面，设计了三个问题，以问卷调查与访谈相结合的方式，诊断学生对它们的认识。本次诊断以本校二（5）班43名学生作为诊断对象。这些学生刚学习完“倍的认识”，尚未进行整数表示量率的相关辨析。

● 诊断问题1：你觉得“3个”“多3个”和“3倍”所表示的意义是否相同？

此诊断问题旨在初步判断学生是否了解一个数在表示数量、相差关系和倍数关系时的差异。对此，42名学生给出了否定的回答，仅有1名学生认为它们所表示的意义相同。结果表明，大多数学生已经意识到三者在意义上存在差异，这为后续的深入探究奠定了基础。

● 诊断问题2：请你用写一写、画一画或举例子等方式，分别表示“3个”“多3个”“3倍”的具体含义。

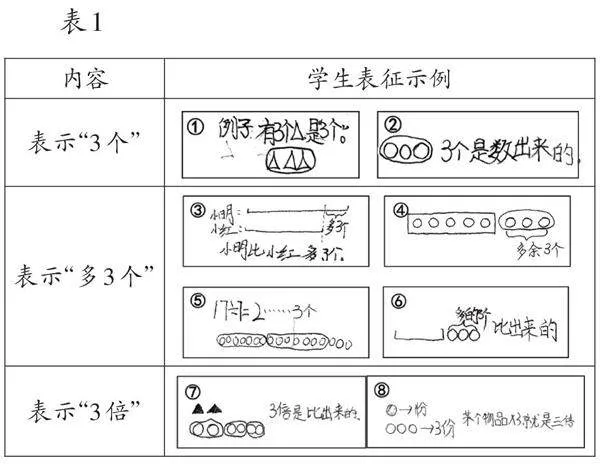
此诊断问题旨在进一步检验学生能否用文字、图式或例子等多种形式表征“3个”“多3个”“3倍”的不同含义。表1是学生的具体表征情况，展现了他们对这三个概念的理解和应用能力。

从上述学生表征情况可知，学生能够运用画图、举例等方式来表示这三个概念的含义。然而，在对“3倍”的表征上，学生表现出模式化的倾向，表征形式缺乏多样性和个性化。

● 诊断问题3：“3个”“多3个”和“3倍”有什么不同？

此诊断问题旨在评估学生能否在理解的基础上，对“3个”“多3个”和“3倍”的差异作出概括性的描述。在访谈中，部分学生能够较为准确地说明三者的区别，如“3个”仅表示具体数量，“多3个”需要通过比较两个数量的差值得出，“3倍”则指比较量中包含3个标准量。然而，仍有部分学生在描述区别时存在困难，教师教学时需为他们提供适当的支持，以帮助他们理解三者的差异。

三、设置核心任务，构建量率意义

基于教学内容与学生学情，教师教学时应设置结构化的核心任务，精心选择学习材料，引导学生依托任务和材料进行深入思辨，从而完成对数的量率意义的建构。

（一）概念探究：辨析图式，建构概念

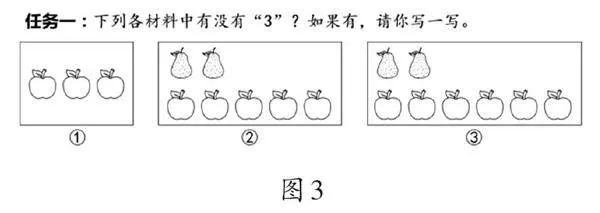
学习材料对概念的形成具有至关重要的作用。教学中，可通过梳理知识点的学习进阶路径、区分相近概念的异同等方式，设计富有思辨性的学习材料，让学生通过思辨真正把握概念的本质及其内在关系。例如，在“倍的认识”的教学中，教师可通过设计结构化学习材料（如图3），整体呈现这些前概念，并引导学生对它们进行辨析。

任务一提供了三幅图式，这三份材料分别描述了“苹果有3个”（材料①）、“苹果的个数比梨多3个”（材料②）、“苹果的个数是梨的3倍”（材料③），分别指向具体数量、相差关系和倍数关系。学生需要仔细观察这三份材料，并进行深入分析。而为了帮助学生辨析这三个概念，教师应将理解层级进行细分，并针对每个层级精心设计问题链，引导学生逐步深入，初步建构倍的概念。具体如下。

层级1：明确三个“3”的意义，重点突出对“3倍”的理解，初步形成对倍的感知。

问题1：三个“3”分别表示什么含义？

层级2：感悟具体数量是数出来的、数量关系是比出来的，初步感知数量的绝对性和关系的相对性。

问题2：三个“3”是怎么得到的？

层级3：感悟相差关系比个数，倍数关系比份数。

问题3：材料②和材料③的“3”都是比出来的，它们在比较时有什么不同？

（二）变式练习：辨析图式，内化概念

变式练习有助于实现对概念的深度理解。通过任务一，学生已初步建构了3倍概念。在此基础上，教师应对学习材料进行改造，引导学生深入探究倍的概念。

1.改变标准量

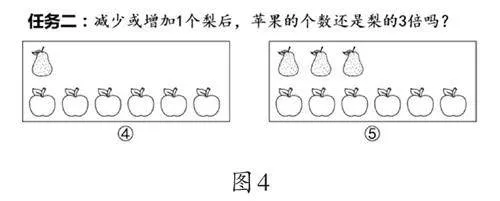
标准量是倍数关系中极其重要的元素，两个数量间存在“几倍”关系由标准量的大小决定，是倍数的度量标准。在倍概念的深度理解阶段，教师可通过改变标准量（如图4），让学生判断苹果数量和梨数量间的关系，从而帮助学生巩固对倍的理解，同时突出标准量的重要性。

在任务二中，两则材料分别描述“苹果个数是梨的6倍”与“苹果个数是梨的2倍”。基于此，教师应引导学生思考：为什么苹果数量不变的情况下，倍数关系也会发生变化？经过讨论交流，学生发现苹果个数与梨个数的倍数关系，关键在于标准量（梨的个数）。比较量（苹果的个数）中包含几个标准量（梨的个数），即表示苹果个数是梨的几倍。这种标准量变化后的倍数判断，不仅强化了学生对倍概念的解释，还突出了倍数关系的本质属性。

2.改变比较量

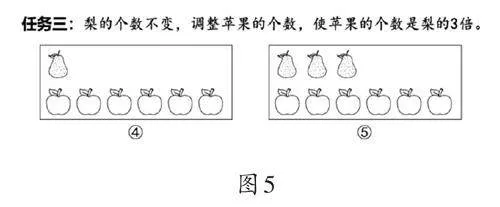
除了改变标准量，还可以通过改变比较量来改造学习材料。在保持标准量不变的前提下，教师可要求学生根据固定的倍数来改变比较量（如图5）。学生需要依据倍数关系的本质属性，即“比较量中包含几个标准量就是几倍”来准确改变比较量。

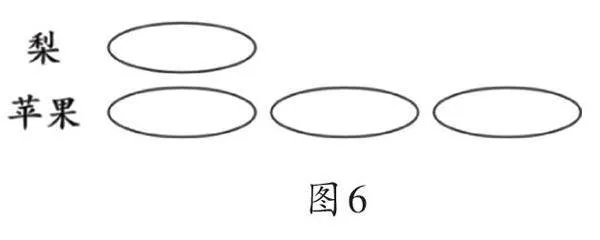
在任务三的学习中，教师要引导学生借助3倍的模型进行逆推（如图6）。具体而言，先确定标准量梨的个数，再根据3倍关系计算出苹果的数量，最后与原来的苹果数量进行比较，决定增减的数量。由此，在改变比较量的过程中，促进倍的结构模型逐渐形成。

（三）结构联结：关联整体，深化概念

结构联结对于培养学生的“整体性思维”具有重要意义，有助于他们构建更为完善的认知结构。

1.关联度量，感悟本质

在倍概念的建构过程中，教师需强调通过标准量来刻画比较量。在结构联结环节，教师应将对倍概念的理解提升到度量层面，引导学生深入理解一倍数和多倍数之间的内在关系，从而培养学生的度量思维。

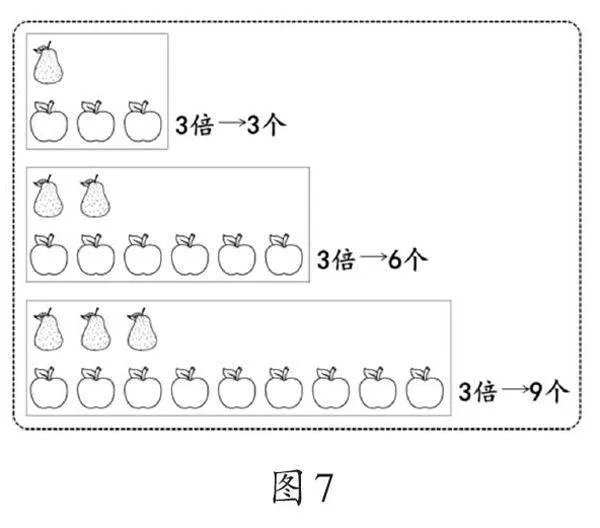
为实现倍概念与度量之间的一致性，教师可利用前述任务中的学习材料（如图7），采用递进式追问的教学策略，助推学生对概念理解的深化和拓展。具体追问如下：（1）苹果和梨的数量各不相同，为什么都能表示苹果的数量是梨的3倍？（2）苹果个数都是梨的3倍，为什么分别对应3个、6个和9个？（3）3倍还可能表示谁和谁的倍数关系？此时的3倍对应多少？

2.关联量率，区分意义

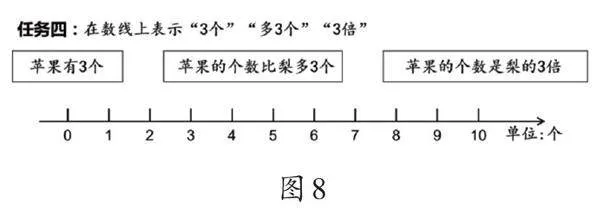
实际上，倍概念的本质是比率（“率”），即对两个数量份数的比较，其核心结构为“乘法结构”。在“倍的认识”的学习中，学生开始接触到一个数同时表示量率双重意义的情境。根据上述学情的诊断分析，此时学生已具备一定感悟量率意义的经验基础。教师教学时可以借助数线模型，引导学生在数线上寻找“量”与“率”（如图8），从而感悟量率意义的区别。

在任务四的学习中，学生在表征“3个”和“多3个”的过程中，可能出现多种不同的表达方式。教师应借助比较分析，引导学生发现数线上任意3段都能表示这两种意义。尽管所选取的3段位置不同，但其段数却是相等的，这体现了“3”在表示具体数量时的绝对性。在表征“3倍”时，多数学生可能受图7中三幅“3倍”图的影响，认为3段、6段、9段都能表示“3倍”。然而，这种理解可能会引发学生的思维冲突，即“3段、6段、9段表示的是具体数量，还是3倍这个数量之间的关系？3倍关系是否也能用数段数的方法表示出来？”针对这些疑问，教师应引导学生进行讨论与交流，明确当“3”表示具体数量时，能在数线上直接找到确切的段数。当“3”表示数量之间的倍数关系时，这种关系无法在数线上用每个点直接表示出来（可以多个点表示）。但当3倍关系明确时，对应的数量可以根据标准量的变化而进行相应调整，因此具有相对性。

数既是对数量的抽象，也是对数量关系的抽象。在教学中，教师应当从“计数单位”和“数量关系”两个基本概念出发，构建数概念的长程教学。特别要注意的是，数的关系意义往往容易被忽视，因此教师需要打破分数才能表示量率意义的固有观念，从具有基础意义的“倍”开始逐步渗透量率的概念。总的来说，量率意义应贯穿教学始终，循序渐进，体现整体性的关联和阶段性的渗透，确保教学的全面性和深度。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］李国强.2022年版课标中“数量关系”主题的价值意蕴与教学策略［J］.教学月刊·小学版（数学），2022（4）：9-14.

［3］杨春琴.把握关系结构" "建构倍的模型：“倍的认识”教材分析与教学建议［J］.小学数学教育，2024（6）：18-20.