思维可视化在初中几何教学中的实践与思考
丁永

摘要:新课标课程理念中明确提出实施促进学生发展的教学活动,体现学生是学习的主体,教师是学习的组织者、引导者与合作者.为了更好地落实这一理念,鼓励学生大胆质疑,引导学生积极探索,展示自己的思维过程和思考成果,思维可视化的研究显得具有十分重要的意义.本案例通过探索三角形全等的条件“边边角”的教学,展示思维可视化在学生进行探索学习过程中的作用和价值.
关键词:思维可视化;三角形全等;边边角
1 思维可视化
随着教育教学的不断进步,思维可视化研究在教学中的研究越来越有价值.尤其对于初中数学的学习,怎样将抽象的数学形象地体现出来,将思维可视化便具有非常重要的意义,不仅能够提升学生学习数学的兴趣,还能调动学生学习数学的积极性.基于这样的教学目的,本文中以探索三角形全等的条件“边边角”为例对数学思维的可视化进行分析,并采取合理的方法提高学生分析问题和解决问题的能力.
关于三角形全等的证明,多少年来有许多教师都进行过各种尝试,课堂教学在向更深更远更广处推进,课堂教学更加追求完善,更加贴近学情.本节课基于学生已有的基本活动经验,从学生的最近发展区出发,通过探究活动将思维可视化,促使学生参与其中,提升分析问题和解决问题的能力.
2 教学过程
2.1 复习回顾
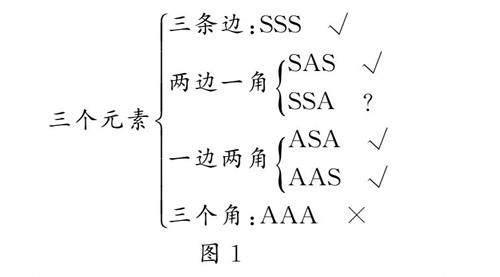
在探索三角形全等的条件时,经过探索发现需要三个条件才能证明两个三角形全等.通过问答的方式复习回顾,具体研究内容如图1.
三个元素三条边:SSS √两边一角SAS √SSA ?一边两角ASA √AAS √三个角:AAA ×
众所周知,对于“SSA”能否判断两个三角形全等并未进行研究,结果到底如何?通过一个设问,顺理成章地引出本节的研究主题.
2.2 活动探索
满足“两边分别相等且其中一组等边的对角相等的两个三角形”是否全等?即在△ABC和△DEF中,AB=DE,AC=DF,∠B=∠E,那么△ABC≌△DEF吗?此时学生的观点出现了分歧,于是教师抛出问题:“如果觉得可以判定全等,请予以证明;若不可以判定全等,请画出反例.”
生1:可以对∠B进行分类讨论,当它是直角时,那么这两个三角形都是直角三角形,此时就可以用“HL”直接证明两个三角形全等.
生2:当∠B为钝角或锐角时不一定全等.
生3:当∠B为钝角应该也可以全等.
随即让学生探索∠B为钝角时,若可以判定全等,请予以证明;若不可以判定全等,请画出反例.将课堂还给学生,留足时间让学生探索.
教师在巡视中发现有的学生束手无策,有的学生在作辅助线,此时教师给学生的探索按下“暂停键”,投屏展示了一名学生画的图及辅助线的作法,并追问这名学生为什么要这样画辅助线(如图2).
生4:因为直可以用“HL”直接证明两个直角三角形全等,所以我想能不能把钝角三角形转化为直角三角形,从而进一步解决问题.
这个过程已经将思维可视化,具体包括两个方面:一是让学生将自己的想法说出来,通过“说”来“可视化”;二是把学生的思考方式和思考过程投屏展示出来,把抽象的思维通过“画”来“可视化”.
教师在巡视中发现,有学生利用辅助线可以证明出△AMB≌△DNE,但是却无法继续,探索再一次停止.此时教师的主导性再次体现出来.
追问学生“欲证明△ABC≌△DEF,还缺什么条件?△AMB≌△DNE对证明有何帮助?”此处激发学生去思考由“已知”到“可知”、由“可知”到“未知”中间还缺什么条件.教师在教学过程中起到“穿针引线”的作用,将探索的权利交给学生.
生5:要证明△ABC≌△DEF还缺一个角,因为“SSA”不能证明两个三角形全等,所以接下来要考虑怎样可以再得到这两个三角形有一对角相等,那样就可以利用“ASA”或者“AAS”来证明△ABC≌△DEF.
生6:通过证明△AMB≌△DNE可得到AM=DN,然后结合已知条件AC=DF,从而可以利用“HL”证明Rt△AMC≌Rt△DNF,于是得到∠C=∠F,如此便提供了一对相等的角,进而可以利用“AAS”来证明△ABC≌△DEF.
教师让学生把完整的证明过程写出来,并投屏展示,此时通过“写”将学生的思维“可视化”.
师:接下来你准备如何继续研究?
生7:接下来考虑∠B为锐角的情况.
师:若可以判定全等,请予以证明;若不可以判定全等,请画出反例.让思维可视化继续发生.
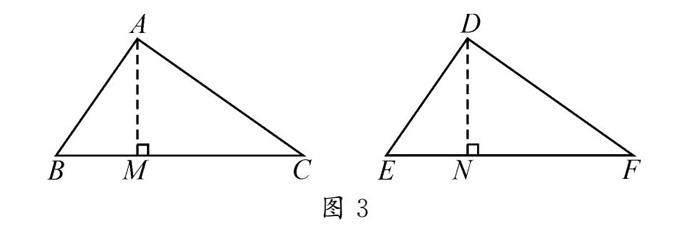
生8:我认为可以,模仿刚才证明钝角三角形全等的方法即可证明.
投屏展示生8的图形(图3),并请他简述证明过程.
先利用“AAS”证明△AMB≌△DNE,从而得到AM=DN,再结合已知条件AC=DF,利用“HL”证明Rt△AMC≌Rt△DNF,于是得到∠C=∠F,如此便提供了一对相等的角,最后可以利用“AAS”来证明△ABC≌△DEF.
生9:我认为不可以,能画出反例,如图4.
师:这到底是为什么?请观察、思考为何会出现这种现象.
将思维可视化向更深更远处走去,继续挖掘学生的思维潜力,激发学生研究的内在动力.
生10:通过图形可以看出,当AB
生11:当AB=AC时,可以画出两个图形全等.
师:你们总结得非常好.根据题目已经条件“两边一角”,我们先对“一角”进行分类,一个角可以是锐角、直角、钝角;接着我们顺理成章地对这两条边进行分类,即AB
∠B钝角√直角√
锐角AB<AC√
AB=AC√
AB<AC×
师:综上,利用“SSA”不能判定两个三角形全等.
3 教学思考
苏联数学教育家斯托利亚尔曾说:“数学教学是数学思维活动的教学.”新课标也明确指出,数学教学不仅要教给学生数学知识,而且要提示获取知识的思维过程,提出“发展思维能力是培养能力的核心”[1].在问题的引导下,学生亲身经历,体验探索方法,经历数学思维的过程,体会“实践出真知”.
3.1 提升思维能力,培养思辨意识
学生在交流展示中,体会到思维碰撞带来的灵感,也会发现自己的能力远超过自己的想象.这样在思考的过程中增强了学生学习数学的动力与自信心,唤醒了学生的参与意识,激发了学生的思辨意识与创新意识.
3.2 展示思维过程,交流思想方法
通过说、写、画、操作、讨论、实验等不同方式,将学生的思维过程全方位“可视化”展示出来.可视化之后,教师便可根据学生的最近发展区设计下一个环节,提出下一个问题,让课堂充满张力,让互动与生成相得益彰.
3.3 完善知识系统,提高教学能力
通过本节课内容的学习和研究,探索三角形全等的过程会更加完整,学生的知识结构也更加系统.教师在备课的过程中不能过多地停留在研究教材上,还要去研究如何设计问题、如何将学生的思维可视化、如何让学生自主进行学习探究,让学生成为学习的主体.在备课时多去研究教师如何成为教学的主导者,如何激发学生内驱力,如何调动学生积极性,如何让学生思维可视化,让学生始终是课堂的主体.
参考文献:
[1]李军.发展学生数学思维能力的路径探析[J].中学数学教学参考,2021(35):63-66.

