基于“微创”教材的初中学科大单元教学
徐亮
摘要:审视教材、研究教材、微创教材,更为科学地体现了教师自主研究和自主创新的专业特点.文章以“平行四边形”第一课时的教学为例,谈了如何“微创”教材,启迪学生的智慧,发展数学核心素养.
关键词:教材;数学核心素养;微创
研究教材和学生是上好数学课的前提.然不少教师在从教中往往秉持“敬畏教材,教教材”的态度,使得数学教学无法真正意义上深入到学生的数学思维.审视教材、研究教材、微创教材,显而易见更为科学地体现了教师自主研究和自主创新的专业特点,只有这样,才让数学课堂时时迸发精彩的思维火花,才能让学生在思维碰撞中启迪智慧,水到渠成地发展数学核心素养.
1 课前思考
当前教育教学领域将数学核心素养的培养与发展视为新热点,这就需要教师从核心素养的高度实施有效教学,让学生在深度学习中发展数学核心素养.当然,教材是基于“新课标”编写的,为教师的教提供了主题、线索和内容,因此教师需站在审视的高度,多番研读与分析教材,这样,才能创造性地使用教材来设计教学.
下面笔者以“平行四边形”第一课时为例,谈谈如何“微创”教材,发展数学核心素养.然作为一种特殊的四边形,平行四边形是几何领域中的一种基本几何图形.创新设计教学过程,凸显平行四边形的本质,引领学生深度探究平行四边形的性质,以促使学生获得对性质的深度理解,是笔者创新设计的主要思路.
2 “平行四边形”第一课时的教学新设计
2.1 问题情境,自然引入
活动一:说一说,做一做.
问题1 请回忆已学的三角形相关知识,说一说特殊三角形有哪些?
问题2 该如何给一般三角形添加条件才能得到等腰三角形?直角三角形呢?
问题3 平行四边形必定是一个四边形,那关键词“平行”该添加在四边形定义中的何处?请试着定义平行四边形.
问题4 观察定义,你能说出平行四边形的本质特征吗?
问题5 试着例举日常生活中一些平行四边形的例子.
问题6 你觉得梯形是平行四边形吗?
问题7 请在草稿纸上作出一个平行四边形,并说一说作图的依据.
设计说明:结合教材的编排意图和具体学情,笔者从单元整体设计的视角着手设计,以提问的形式呈现三角形的相关知识,并以此作为知识的生长点促进平行四边形定义的自然生成.审视教材,但依旧没有脱离教材,只是颠覆了教材的呈现方式,从学生的需求出发,让问题解决与数学思考真实发生,学生或思考、或讨论、或操作,在定义的过程中深刻认识定义的本质,实现深度学习,更重要的是,极好地培养了类比推理和归纳概括素养.
2.2 创新活动,探索新知
活动二:忆一忆,想一想.
问题1 回顾等腰三角形的学习历程,试着阐述研究几何图形的一般思路及研究角度.
问题2 类比等腰三角形性质的研究策略,试着研究平行四边形的性质,并说一说你的研究角度.
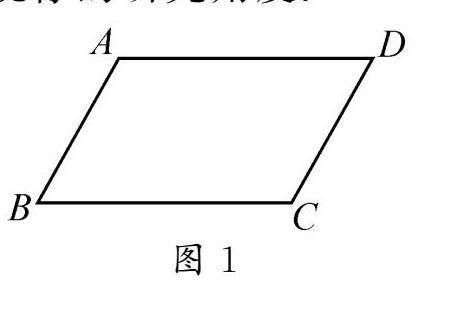
问题3 既然我们已经对平行四边形有了一些认识,除了两组对边分别平行的性质,你还知道它的哪些性质?先观察刚才大家所画的平行四边形(如图1),再大胆猜想,并借助学具验证你的猜想.
学生猜想:①AB=CD,AD=BC;②∠A=∠C,∠B=∠D.
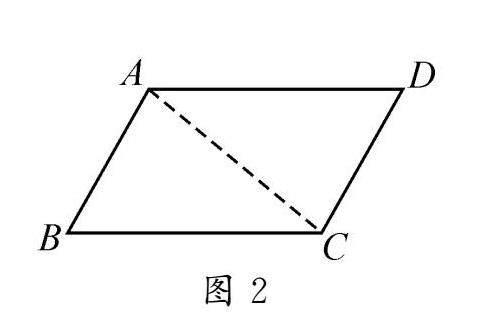
问题4 以小组合作学习的形式证明上述猜想.〔点拨:①一般来说,学习几何知识我们是如何证明两条线段相等或两个角相等的?②连接对角线AC(如图2)的方法你是如何想到的?③还有其他证明两组角相等的方法吗?〕
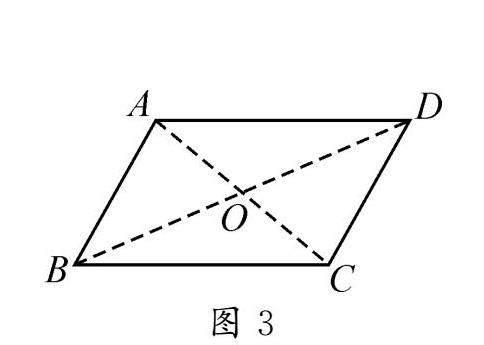
问题5 如图3,继续连接另一条对角线BD,使得AC,BD交于点O,你现在能发现什么?
学生猜想:AO=CO,BO=DO.
问题6 试着证明你的猜想.
问题7 继续从对称性角度研究平行四边形,你发现了什么?
设计说明:在这一环节,笔者设计一系列实践活动,引领学生亲历知识发现的过程,获得切身体验的同时深刻理解知识,感悟思想方法.基于对教材细节的挖掘和把握设计探究活动,不仅可以帮助学生深度思考和深度探索,而且还可以通过问题解决的过程来强化学生的认识,以此进一步发展学生的合情推理和演绎推理素养[1].深入解读教材和审视教材,不断发掘和延伸,往往可以在教学中“物化”出深度精彩.
2.3 课堂练习,巩固认识
活动三:想一想,练一练.
练习1 如图4,已知ABCD.
(1)若∠A=40°,试求∠B,∠C的度数;
(2)若AB=6,BC=8,试求ABCD的周长;
(3)若周长是20,且AB∶BC=2∶3,试求AB;
(4)若AD上有一点E,BC上有一点F,且AF∥CE.证明:DE=BF,∠BAF=∠DCE.
练习2 如图5所示,已知ABCD的对角线AC,BD交于点O,且AC=6,BD=10.
(1)若BC=7,试求出△AOD的周长;
(2)若BC=m,试求出m的取值范围;
(3)若AC⊥BD,试求AB.
设计说明:通过挖掘教材来创新设计课堂练习,可以促进学生自然而然地迁移新知.这里,练习设计的成功主要体现在不仅拾级而上地串联了教材中的例习题,而且通过思维的点拨和智慧的追问,延伸了“问题链”,帮助学生巩固和迁移了新知,同时实现了思维水平的跃升.
2.4 课堂小结,深化认识
活动四:忆一忆,议一议.
问题1 回顾本课的学习过程,说一说我们着手研究平行四边形性质的角度.
问题2 本课学习中所涉的思想方法有哪些?
问题3 你觉得之后我们还可以从哪些角度着手研究平行四边形?
设计说明:本环节中,借助于课堂小结,带领学生梳理所学,感悟思想方法.在回顾、反思和概括的过程中,完成了知识框架体系的自然构建,并为后续的探究和学习指明了方向,更重要的是对培养数学概括和数学抽象素养十分有利.
2.5 拓展延伸,发展思维
活动五:想一想,做一做.
问题 以图5为基础,继续过点O任意作出直线EF,交线段AD于点E,交线段BC于点F,观察后你发现了什么?请试着用不同方法证明你的发现.
变式 若直线EF分别交直线AB,DC于点E、F,观察后你又能发现什么?
设计说明:基于教材中拓展延伸题的设计,笔者创造性地设计了变式问题,使静态的问题情境以动态的方式复活,同时从学生的思维路径出发要求学生提出问题并解决问题.这样一来,由于问题是学生自己提出的,自然有了研究和解决的欲望,从而真正意义上实现了深度迁移,极好地发展了创新思维能力.
3 一些思考
“微创”教材,首先需要教师深钻教材内部理解编者意图,并能从教与学的需求出发整合教材,通过扩展、串联等方式凸显知识本质,这样才是真正意义上读懂了教材,才能切实用活教材,最终启迪学生的智慧[2].
“微创”教材,还需要教师深入挖掘细节,从具体学情出发由浅入深地设计教学活动,用可操作的教学路径拓展学生数学思考的深度,引领学生深度学习,最终完善学生的认知结构,发展学生数学抽象、数学概括等核心素养[3].
“微创”教材,更需要教师叩问数学的核心本质,创造性地延伸素材,让学生在拉长的问题链中踏阶而上、浅入深出,促使数学思维及内在思想真正落地,生成别样的课堂精彩.
总之,教师只有“微创”教材,才能从真正意义上将教材理念内化为自身的实践,启迪学生的智慧,发展学生的数学核心素养,不断攀登新课程改革的新高度.
参考文献:
[1]王德昌.钻研数学教材的十个关注点[J].教学月刊\5中学版(教学参考),2013(11):62-64.
[2]施正建.合理使用数学教材,激发学生的学习兴趣[J].语数外学习(初中版下旬),2014(4):58.
[3]金莉莉.浅谈在初中教学中如何使用数学教材[J].数学学习与研究,2014(16):45.

