例谈初中数学思维能力提升的关键抓手

杨峰 朱宸材

摘要：本文中从突破思维定势、加强发散思维、强化逆向思维、落实求异思维四个方面重点论述了数学思维能力提升需要注意的关键抓手，为数学思维能力的提升提供了一些教学案例.

关键词：思维能力；关键抓手；思维定式

《义务教育数学新课程标准（2022年版）》针对教学活动方面提出，学生的学习应是一个主动的过程，是独立思考、动手实践、自主探索的过程，应注重激发学生学习的兴趣、引发学生积极思考、加强探究的过程，只有这样才能培养学生良好的学习习惯，逐步形成核心素养.那么在日常教学中，如何突破思维定势，深化学生的探究意识呢？

1 突破思维定势，唤醒学生探究意识

思维定势是一种学习过程中的惯性思维，这种思维往往带给我们的是不假思索，直接根据经验进行判断的心理活动.这种思维活动的特点是呈现惯性延续的特色，是由先前的活动而造成的一种对活动的特殊的心理准备状态或活动的倾向性.这种思维也是我们在数学学习中通过例题讲解给学生形成的一种定势，这种思维往往阻碍着探究意识的觉醒，看到相类似的问题或者表面相同的情境，不由自主凭借之前的理解或认识直接套用相关的方法去解答，缺乏正确的思考.

在教学轴对称相关知识的过程中，常常利用探寻对称点，将折线转化为直线段探求最短路径，遇到立体图形问题，也常常是将立体图形转化为平面图形问题，因此学生在遇到类似问题时不假思索，直接按部就班展开图形，探寻对称点，利用勾股定理进行计算.但是遇到下述问题时却出现了错误.

案例1 如图1，在一个长为6 cm、宽为3 cm、高为4 cm的长方体方块的左下角A点处有一只蚂蚁，它要沿着正方体的表面爬行至右上角的B点去搬运一块食物，探求这个蚂蚁所走的最短路线的长度.

根据经验，把此长方体的一面展开，然后在平面内利用勾股定理求A和B两点间的线段长，即可得到蚂蚁爬行的最短距离.但是长方体却不同于正方体，平面展开图不唯一，故需分情况计算，进行大小比较，再从各个路线中确定最短的路线.通过计算得到了三种情况：其一，展开前面与右面，由勾股定理得AB2＝（6+3）2+42＝97；其二，展开前面与上面，由勾股定理得AB2＝（4+3）2+62＝85；其三，展开左面与上面，由勾股定理得AB2＝（6+4）2+32＝109.经过对比分析，最终确定最短距离为85 cm.

这个案例具有一定的代表性，七年级学生在刚接触时，容易由两点之间线段最短的定势思维带入，对于空间想象能力相对比较薄弱的学生，通过教学软件的模拟展开，化立体为平面不失为一种好的教学尝试.因此，在利用思维定势发挥其正向迁移作用的同时，注意引导学生加强基本概念和规律探究，注意问题的变化特性，切勿将学过的知识僵化地利用在解答过程中，强化学生对公式的灵活运用，准确把握公式的探究过程，让概念、公式基本知识之间建立起科学的联系，真正提高学生的探究能力.

2 加强发散思维，奠定学生探究基础

发散思维是在对问题的研究不能一下确定答案，或者存在较多方面的理解，或者对问题多种答案的思考.常常所说的“一题多解”“一题多问”等形式，在很多资料中称之为“开放问题”.俗话说得好，没有“发散”就没有思考，没有思考就没有“探究”.教学中，教师要精心设计问题情境，激发学生的发散思维，从而逐步养成多层面、多角度感知与认识问题的习惯.

学习轴对称知识后，利用折纸的方法，可以直接剪出一个五角星，并探索其中所隐含的数学道理.学到这里，我们可以引申其中的素材，进一步加强学生的发散思维训练.

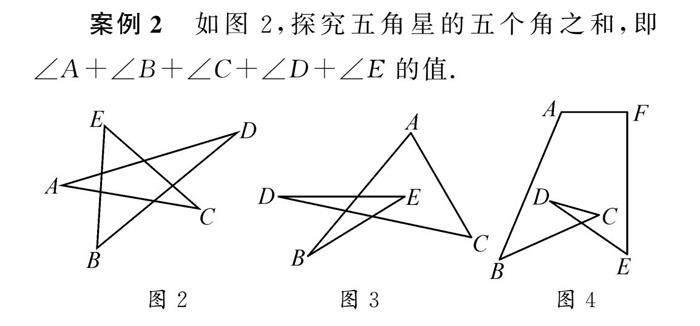
案例2 如图2，探究五角星的五个角之和，即∠A+∠B+∠C+∠D+∠E的值.

显然，上述问题利用三角形的外角性质和内角和定理即可解答.再变换图形样式，如图3，五角之和是不是有变化？这样的图形在解答过程中的思路是不是也是一样？再变化，如图4，六角之和又有什么样的变化呢？一连串的变化，引导学生通过对“五角”问题的探究发散思维.再深入研究，可以将“五角”延伸到“七角”“九角”等问题之中.

3 强化逆向思维，打通学生探究通道

逆向思维，是一种对似乎已成定论的问题或看法重新变换、反向思考的一种思维方式.这种思维具有很大的挑战性，既要有新的思想或方法，又要有独特的观点与理论.在日常教学中，教师要注意有意设置相关障碍，引导学生适时转向思考，借助新的角度重新认识问题，从而找到突破问题的新方法.

如教材中告诉我们平行线具有3个性质，其中性质2和性质3都是利用性质1推导出来的，但是教材中却没给出性质1的推理过程，而是通过测量观察数据得出的，这也便成了数学基本事实，那我们该如何给出证明呢？运用逆向思维来思考，采用反证法证明即可得到结论.类似地，平行线的判定方法也是同样.数学教材中这样的问题非常多，例如引导学生证明结论“在同一平面内，过直线外一点有且仅有一条直线与已知直线垂直”，学生难以入手，若利用逆向思维，假设所求证的结论不成立，经过推理证得结论与基本事实“经过直线外一点，有且只有一条直线与这条直线平行”产生矛盾.从而得证.

逆向思维的强化训练，很容易将复杂的问题简单化，从而提高了解题效率，更是加强了学生对一些较难问题探究的力度，向深度问题进行有力挑战，同时又是对知识的不断深化.自觉运用逆向思维，可以创造更多奇迹.

4 落实求异思维，开辟学生探究天地

求异思维，是指大脑在思维时呈现的一种扩散状态的思维模式，它表现为思维视野广阔，思维呈现出多维发散状.它重点培养学生的发散思维能力.为了更好地激发学生的求异思维，加强探究训练，这需要教师善于捕捉学生思维的闪光点，适时鼓励学生，不怕错误，更不怕失败，从简单入手，直至复杂问题的研究，要有锲而不舍的精神.

加强求异思维，不但可以帮助学生全面理解问题，还能更好地预防“思维定势”.教师在教学中要善于利用教材案例进行训练，培养学生的想象与创新思维，并借助探究能力深化知识探索.

案例3 在△ABC中，两条高BD，CE所在的直线相交于点O.

（1）当∠BAC为锐角时，如图5，求证：∠BOC+∠BAC＝180°.

（2）当∠BAC为钝角时，如图6，请在图中画出相应的高线，并回答（1）中的结论是否成立？

本案例通过改变条件，重新提出新的问题，使结论更加全面.类似的问题正是一步步利用求异思维，将学生推向问题的核心处，激发探究兴趣，以原题为引子，突破自我，拓展思维，在研究问题过程中不断提升自己的理性思维水平和创新能力.

综上，对学生的思维品质的培养，方法有很多种，教师要让学生的思维真正在课堂上活跃起来，这才是课堂训练的根本.抓住教材素材，善于引导、启发，落实学生的学与思、思与练、练与探的能力，从而不断推进学生核心素养的提高，实现育人目标.