“一题一课”型微专题课的教学与思考
陈晨 赵军 徐琳琳


“一题一课”是指教师通过对一道题或一个材料作深入研究,挖掘其内在的学习线索和数学本质,自然、合理和有序地组织学生进行相关的数学探究活动,以达成多维目标的过程[1].
“圆”是初中几何中一个重要的章节,和圆有关的问题中难度较大的要属“隐圆问题”,究其原因在“隐”字上.学生看不到动点的运动轨迹,很难解决好此类问题,因此教师需要结合数学理论引导学生看清它.笔者拟借助“一题一课”授课方式,带领学生对“隐圆问题”进行分类研究,帮助学生归纳总结.
1 教学目标
(1)了解“隐圆问题”的常见类型及解决方法,为后期学习打下基础;
(2)通过“一题一课”的教学方式,培养探究和解决问题的能力.
2 教学过程
2.1 前置问题
如图1,已知⊙O与圆外一点P,求作点P到圆上最近的点A和最远的点B,请作图说明并证明.
分析:通过对圆外一点到圆上的最短距离和最长距离的证明,归纳它们的计算公式,为后面例题的讲解打下基础.证明所得的结论,对解决“隐圆问题”中的最大(小)值非常实用.
解析:如图2,设A′是⊙O上任意一点,r为⊙O的半径.
在△OA′P中,由
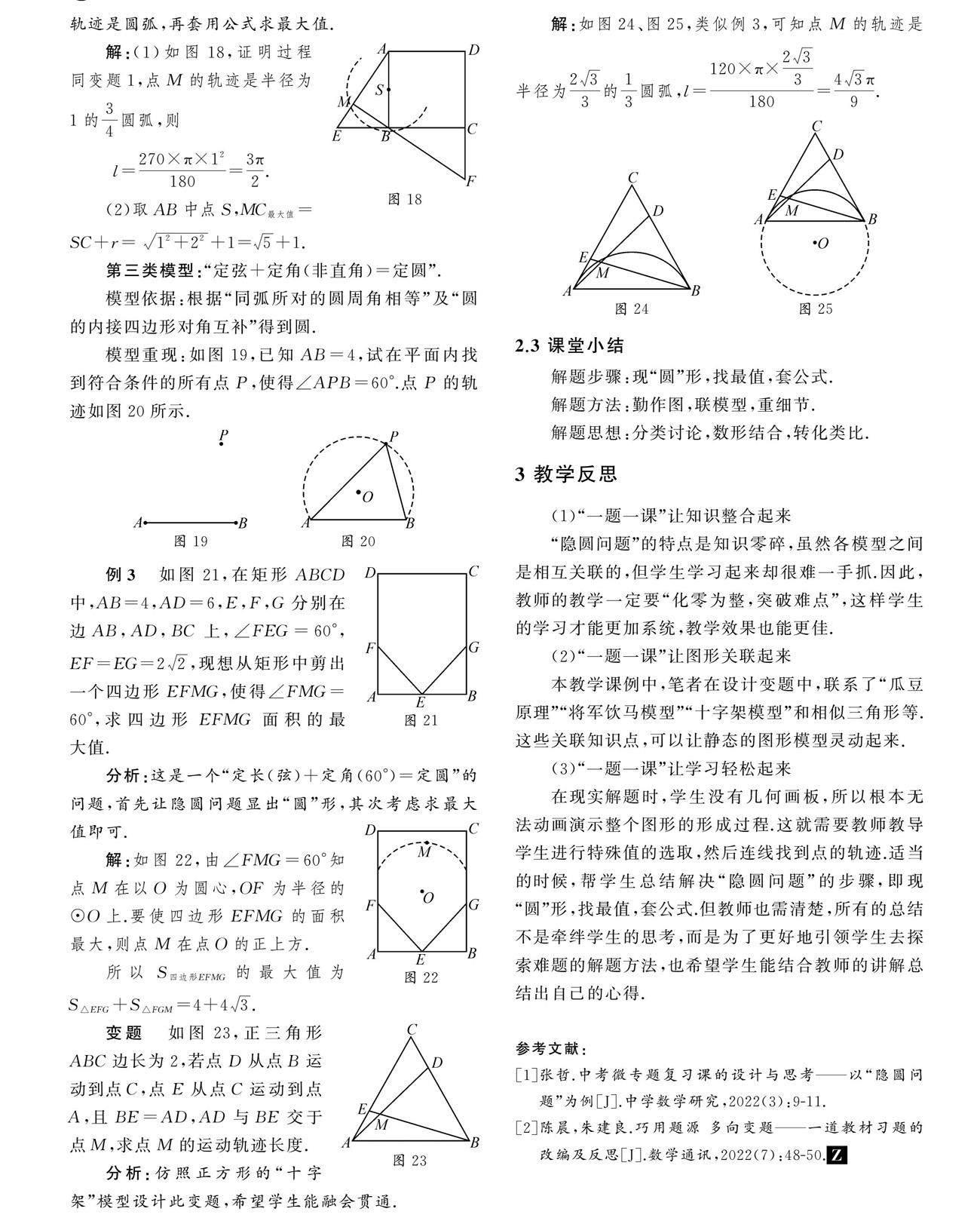
OP OP-OA′ 因为OA=OA′,所以 OP-OA 所以A是⊙O上距离点P最近的点,且最近距离=OP-r. 如图2,在△OA′P中,因为 OP+OA′>A′P,OA′=OB,所以 OP+OB>A′P,即BP>A′P. 所以B是⊙O上距离点P最远的点,且最远距离=OP+r. 2.2 模型探究 第一类模型:“定点+定长=定圆”. 模型依据:根据圆的定义,联系“到定点的距离等于定长的点的集合是圆”. 模型重现:如图3,已知线段AB和点O,试在平面内找到符合条件的所有点M,使得MO=AB.(点M的轨迹就是以点O为圆心,AB长为半径的⊙O,如图4.) 例1 如图5,在矩形ABCD中,AB=4,AD=6,E是AB的中点,F是边BC上任意一点,将△EFB沿着EF所在的直线折叠得到△EFB′,连接B′D,求B′D的最小值. 分析:这是一个“定点+定长=定圆”的问题,经过分析首先引导学生使隐圆的题显出“圆”形,其次考虑求最小值,最后套用“DE-r”求解即可. 解:如图6,因为点B到点E的距离不变,所以点B′的轨迹为以点E为圆心,EB长为半径的圆弧. 因此可得DB′最小值=DE-EB=22+62-2=210-2. 变题1 如图7所示,正方形ABCD的边长为4,将长为4的线段EF的两端放在正方形相邻的两边上同时滑动(即两个端点始终落在正方形的边上).点E从点A出发,按逆时针方向滑动一周,在整个过程中,求线段EF的中点M所经过的路线围成的图形面积. 分析:此题的解题关键是画出点M的运动轨迹,再分析其围成图形的特点,最后计算面积即可. 解:如图8,点M运动所经过的轨迹围成的图形是正方形挖去4个14个圆.因此,所围成的图形面积是16-4π. 变题2 如图9,矩形ABCD中,AB=4,AD=6,现有一条长为4的线段EF,紧贴着矩形的边(即两个端点始终落在矩形的边上),点E从点A出发,按逆时针方向滑动一周.在整个过程中,求线段EF的中点M所经过的路线围成的图形面积. 分析:此题也是先画出点M的运动轨迹,再分析其围成图形的特点,最后计算面积即可. 解:如图10,点M运动所经过的轨迹围成的图形还是矩形挖去4个14个圆,因此所围成的图形面积是24-4π. 第二类模型:“直径+直角=定圆”. 模型依据:根据圆周角定理的推论,寻找“90°的圆周角所对的弦是直径”. 模型重现:如图11,已知线段AB=4,试在平面内找到符合条件的所有点P,使得∠APB=90°.(如图12) 例2 如图13,在矩形ABCD中,AB=4,AD=6,E是一个动点,且AE⊥BE,求线段CE的最小值和最大值. 分析:这是一个“定长(直径)+定角(90°)=定圆”的问题,首先还是让“隐圆问题”显出“圆”形,其次考虑求最小值和最大值,最后分别套用DE-r和DE+r即可. 解:如图14,由∠AEB=90°,可知 点E在以AB为直径的⊙O上. 故CE最小值=CO-r=210-2; CE最大值=CO+r=210+2. 变题1 如图15所示,正方形ABCD的边长为2,若点E从点B运动到点C,同时点F从点C运动到点D,且BE=CF,AE与BF交于点M.(1)求点M的运动轨迹长;(2)求MC的最小值. 分析:这里联系了正方形的“十字架”模型[2],容易证明BF⊥AE,从而得到点M的运动轨迹是圆弧,再套用公式求最小值. 解:(1)如图16,在 正方形ABCD中,有 AB=BC,∠ABC=∠C. 又BE=CF,所以 △ABE≌△BCF,则 AE=BF. 易证AE⊥BF,则点M的轨迹是半径为1的14圆弧,所以l=90×π×12180=π2. (2)取AB中点S,则MC最小值=SC-r=5-1. 变题2 如图17,正方形ABCD边长为2,若点E在线段CB延长线上任意移动,点F在线段DC延长线上任意移动,且BE=CF,AE与BF交于点M.(1)求点M的运动轨迹长度;(2)求MC的最小值. 分析:本题还是联系正方形的“十字架”模型,易证直线BF和AE是垂直关系,从而得到点M的运动轨迹是圆弧,再套用公式求最大值. 解:(1)如图18,证明过程同变题1,点M的轨迹是半径为1的34圆弧, 则 l=270×π×12180=3π2. (2)取AB中点S,MC最大值=SC+r=12+22+1=5+1. 第三类模型:“定弦+定角(非直角)=定圆”. 模型依据:根据“同弧所对的圆周角相等”及“圆的内接四边形对角互补”得到圆. 模型重现:如图19,已知AB=4,试在平面内找到符合条件的所有点P,使得∠APB=60°.点P的轨迹如图20所示. 例3 如图21,在矩形ABCD中,AB=4,AD=6,E,F,G分别在边AB,AD,BC上,∠FEG=60°, EF=EG=22,现想从矩形中剪出一个四边形EFMG,使得∠FMG=60°,求四边形EFMG面积的最大值. 分析:这是一个“定长(弦)+定角(60°)=定圆”的问题,首先让隐圆问题显出“圆”形,其次考虑求最大值即可. 解:如图22,由∠FMG=60°知点M在以O为圆心,OF为半径的⊙O上.要使四边形EFMG的面积最大,则点M在点O的正上方. 所以S四边形EFMG的最大值为S△EFG+S△FGM=4+43. 变题 如图23,正三角形ABC边长为2,若点D从点B运动到点C,点E从点C运动到点A,且BE=AD,AD与BE交于点M,求点M的运动轨迹长度. 分析:仿照正方形的“十字架”模型设计此变题,希望学生能融会贯通. 解:如图24、图25,类似例3,可知点M的轨迹是半径为233的13圆弧,l=120×π×233180=43π9. 2.3 课堂小结 解题步骤:现“圆”形,找最值,套公式. 解题方法:勤作图,联模型,重细节. 解题思想:分类讨论,数形结合,转化类比. 3 教学反思 (1)“一题一课”让知识整合起来 “隐圆问题”的特点是知识零碎,虽然各模型之间是相互关联的,但学生学习起来却很难一手抓.因此,教师的教学一定要“化零为整,突破难点”,这样学生的学习才能更加系统,教学效果也能更佳. (2)“一题一课”让图形关联起来 本教学课例中,笔者在设计变题中,联系了“瓜豆原理”“将军饮马模型”“十字架模型”和相似三角形等.这些关联知识点,可以让静态的图形模型灵动起来. (3)“一题一课”让学习轻松起来 在现实解题时,学生没有几何画板,所以根本无法动画演示整个图形的形成过程.这就需要教师教导学生进行特殊值的选取,然后连线找到点的轨迹.适当的时候,帮学生总结解决“隐圆问题”的步骤,即现“圆”形,找最值,套公式. 但教师也需清楚,所有的总结不是牵绊学生的思考,而是为了更好地引领学生去探索难题的解题方法,也希望学生能结合教师的讲解总结出自己的心得. 参考文献: [1]张哲.中考微专题复习课的设计与思考——以“隐圆问题”为例[J].中学数学研究,2022(3):9-11. [2]陈晨,朱建良.巧用题源 多向变题——一道教材习题的改编及反思[J].数学通讯,2022(7):48-50.

