体会—理解—内化：高中递归程序教学三步*

【摘 要】高中信息技术教学中，递归可将复杂问题简单化，且递归程序代码较为简洁，是程序设计必备的算法。递归同时也是高中信息技术课标要求学生所掌握的算法。在教学中，教师可从体会递归的原理、深层次理解递归、内化递归思维三个方面展开，促进学生理解递归，进而形成递归思维。

【关键词】高中信息技术；递归算法；递归程序

【中图分类号】G633.67  【文献标志码】A  【文章编号】1005-6009（2024）19-0071-03

【作者简介】张宏亮，南京市第二十九中学（南京，210036）教师，一级教师。

递归在程序设计领域是一种算法，递归程序就是利用递归算法编写的程序代码。其中递归算法的实现依赖于函数。因此，在一个函数的函数体中可以直接或间接地调用该函数本身，这样的函数称为递归函数，递归函数直接或间接调用自身的过程叫作递归。［1］

在实际教学中，递归程序虽然代码简洁，但函数逐层调用自己的过程过于复杂，有时还要逐层返回去执行上一层后续的代码，教师难讲解清楚，学生易陷入思维混乱。因此，在进行递归程序教学时，教师应注意设置情境，引导学生从形象思维顺利过渡到抽象思维，理解递归的本质以及递归执行的原理与过程。

一、体会递归的原理

体会递归的原理是深入学习递归的第一步。递归的基本思想就是把一个大的复杂问题逐层转化为一个与原问题相似但规模较小的子问题来求解，即化繁为简、以大化小。

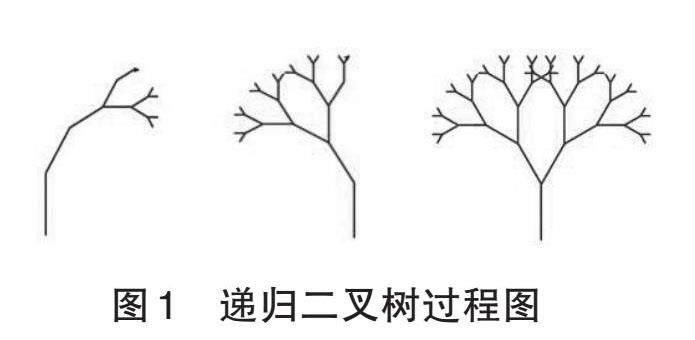
笔者认为，教师在教学中可选取能体现递归的原理的案例，让学生直观感受的同时，激发其继续探究递归的兴趣。案例的选取可从生活中的递归入手。如分形图，利用递归算法可以模拟出传统的几何方法所不能描述的自然景观，将复杂的景物用简单的规则来生成［2］，从视觉上刺激学生。如何引导学生在直观感受的同时领悟其中的递归思想，是教师教学的重点。笔者认为，可以从引导学生利用计算思维分析案例入手。计算思维解决问题一般分为4个步骤，即分解问题、模式识别、抽象化、算法。以图1中的递归二叉树案例为例。

第一步：分解问题，教师呈现递归二叉树代码运行过程的动画，让学生观察它是如何将递归二叉树图形逐步转化为一个个规模较小的子图形的，使学生意识到可将复杂的图形分解为较小的简单图形来求解。

第二步：模式识别，引导学生发现原图形和子图形的相似之处。学生从动画演示中易发现二者不仅形状相似，且画法相同。

第三步：抽象化，引导学生抽象出原图形和子图形本质的画法，即“绘制右子树—回到树枝节点—绘制左子树—回到树枝节点”。

第四步：算法，不断重复执行第三步抽象得到的步骤，即可画出递归二叉树。此时学生已感知到了原问题与子问题的关系，也有了将复杂问题分解成小问题来解决的意识。据此，教师可以引出递归算法的基本思想。

二、深层次理解递归

经过递归思想的渗透，学生即可编写程序。但在编写程序时，学生往往会无从下手，尤其是对函数自己调用自己的过程感到困惑。因此，本部分教学的难点在于使学生深层次理解递归，理解函数自己调用自己来解决问题的原理与过程。

教学递归程序的前提是学生已经掌握了自定义函数。首先，笔者让学生用递归思想去分析问题，明确自定义函数。其次，用嵌套的形式辅助学生理解递归的执行过程，即递推然后回归。具体以年龄问题为例阐述如下。

问题情境：5个学生在一起，第5个学生说他比第4个学生大两岁，第4个学生说他比第3个学生大两岁，第3个学生说他比第2个学生大两岁，第2个学生说他比第1个学生大两岁，第1个学生说他今年10岁，请问第5个学生今年几岁？

第一步：按照递归思想分析该问题，以大化小，可知要求第5个人年龄，先求第4个人年龄再加2，求第4个人年龄要先求第3个人年龄再加2，以此类推。接下来逐步形成自定义函数，可以发现：计算某个人的年龄是重复的动作，即其等于计算前一个人的年龄加2，如果是第一个人年龄，答案就是10。可自定义一个函数为age（），功能为求某个人的年龄。设变量n代表“当前同学”，则可得到代码（见图2）。

第二步：用嵌套的形式辅助学生理解递归的执行过程。递归的本质是函数的重复执行，只不过是通过函数自己嵌套自己的方式来实现的。笔者认为，此处可以让学生动手实践，体会和感悟函数的重复执行过程，如可设计如图3所示的试一试活动。实践过程中学生会发现这个程序会不断输出某个数，直至报错，教师可借此顺利引出解答此题要给出重复执行的终止条件，否则函数会无限地反复调用，从而陷入死循环。

经过以上学习，教师引导学生再回过头来分析计算年龄的递归程序，学生易体会到虽然age（）函数仅有4行代码，但实际上该age（）函数在不断地重复执行。由于age（）函数执行过程中涉及回归，笔者认为此处可展开嵌套，用图形的形式将抽象的东西具象化，辅助学生理解递归过程（见图4）。根据嵌套的执行原理，即先递推到最内层嵌套，只有当最内层嵌套解决了，才返回上一层嵌套去执行后续的代码，先是逐层递推进去，然后再逐层返回，且每一层嵌套都是age（）函数本身，学生也就理解了递归“自己”逐层向内嵌套“自己”的原理——先逐层嵌套进行递推，再逐层返回进行回归。

经过以上教学，学生明确年龄问题的递归程序完整代码如图5所示，递归终止条件为n==1。递归编写的代码简洁易懂。

三、内化递归思维

图5中的年龄问题较简单，用普通的循环就可以解决，但是现实中学生往往会面临复杂的问题，解决这类复杂问题时就需要用到递归思维。因此，在教学中，教师要引导学生通过递归的案例形成递归思维，解决复杂问题。

教师可设计经典的案例培养学生的递归思维，使其学会分解并抽象复杂问题。如走台阶问题：一个10级台阶的楼梯，如果每次只能走一个台阶或者两个台阶，那么有多少种走法？

第一步：以大化小，逐层分解问题。设问：逐步缩小问题规模，分解的若干子问题分别是什么？其中最小可直接解决的子问题是什么？第二步：寻找关联，抽象问题。设问：原问题与分解的若干子问题有何关联，能否建立计算模型？学生容易发现原问题和子问题解法相同，即n阶台阶走法=（n-1阶台阶走法）+（n-2阶台阶走法），接着教师引导学生将解决问题的方法抽象成自定义函数，即递归函数。第三步：整理算法，编写程序。

递归的优势在于编写的代码简洁，解决问题的逻辑一目了然，尤其是用于解决复杂问题。但递归需要较多的时间和空间，若递归的深度过大还会导致系统崩溃。因此，在面对问题时，应根据实际情况选择是否用递归。教师在教学递归程序时，若可以引导学生快速找到循环解决的方法，则优先用循环解决，反之尝试用递归思维去解决，也可将递归转为非递归程序。

【参考文献】

［1］谭浩强.C程序设计教程［M］.北京：清华大学出版社，2007：153.

［2］张学军， 张萍.递归程序探讨［J］.兰州文理学院学报：自然科学版，2002，16（1）：65-69.