初中数学几何问题解题技巧研究
张玉峰
【摘要】随着教育事业的高质量发展,新课标与素质教育落实均愈发深入,这对初中数学教学提出更高质量要求,其中,几何是初中数学的重点,也是学生学习的难点.基于此,为强化学生解题能力,培养他们的解题思维,文章探究、总结了初中数学几何问题的解题技巧,结合具体几何问题梳理各种解题技巧下的思路与方法,具体包括辅助线法、平移法、代数法、逆向思维法、建系法等,梳理技巧应用要点,总结解题关键,旨在为教师传授学生解题技巧、提高学生解题能力提供帮助.
【关键词】几何问题;解题技巧;初中数学
引 言
初中数学几何问题具有逻辑性强、知识面广等特点,对学生解题思维和能力提出了较高要求.几何类问题的解题技巧相对较多,不同的题型,解题期间灵活使用不同的解题技巧可以让解题速度加倍.为有效提高学生的几何解题能力,研究技巧应用要点是必要的.
一、辅助线法
在初中数学中,常用的解题技巧是添加辅助线,几何问题作为初中数学的重要题型,辅助线法应用极为常见,应用此方法的目的在于通过辅助线细化整体大问题,或是将零散的问题条件整合到一处,从而快速敏捷地疏通思路,最终成功解决问题.但是,辅助线的使用并非随意、盲目的,需要根据几何条件和几何基础知识,让辅助线的使用具有一定合理性.例如,在非直角三角形的几何问题中,若是在该三角形中出现特殊角,那么可下意识尝试作垂线作为辅助线,构建直角三角形辅助解题;在圆形的几何问题中,可下意识尝试作能够构造出90°圆周角的辅助线;在涉及梯形的几何问题中,如果题中存在关于梯形的腰的中点,那么可尝试作能够构造出梯形中位线的辅助线,或是连接一个顶点和腰的中点,然后进行相应的延长从而构造出全等三角形的方式作辅助线.初中数学几何问题难度适中,通过适当总结辅助线法的作图规律与技巧,能够在短时间内快速找到解决几何问题的突破口,开拓学生的解题思路,提升他们的空间思维能力.
根据图1可知,无法在这种形式下直接求出AD和BD的值,在应用辅助线法的情况下,解题思路应该是尽量将求取的两条线段转化至一条线段中,即:作辅助线DE,使其与AB垂直,垂足为点E.通过作这条辅助线,可有效降低解题难度,简化解题逻辑,从而求出最小值的大小.
二、平移法
解决数学几何问题的平移法,主要通过平移某些图形的方式构建新的图形,从而简化解题步骤.该解题技巧应用的重点在于找出能用平移来求解的图形,具体思路为:根据已知条件平移图形———替换所求图形———求出结果.一般情况下,平移对象较多,可以是圆、直线、角、线段,甚至是整个图形,该解题技巧只会带来图形位置的变化,不会对图形大小、形状造成影响.在初中数学几何问题中应用平移法时,几种情况较为关键:平移前后的线段平行;对应角两边分别平行且方向一致;对应点连线所得线段相等且平行.一旦掌握这一解题技巧,学生遇到相似题型,将会快速掌握习题考点与解题思路,挖掘隐藏的数学要素,实现快速解题.
例2 如图2(a)所示,图中的A,B代表着两个农庄,l1和l2为河的两岸,现在农庄主人想垂直于河流修一座桥,借此缩短农庄A,B之间的距离,若想实现距离最短,桥应该修在哪里?
通过题干可知,该几何问题的本质是求两个点之间的最短距离,与之有关的是“两点之间线段最短”.在该思路下,可转化图中的一些线段,通过平移转化为两点之间线段最短的求取问题.平移思路如图2(b)所示.
运用平移法解答此道几何问题时,可先作BB′垂直于l2,线段BB′与两岸之间的距离相等,连接AB′,与河道l1的交点为点P,PD垂直于l2,构建平行四边形.利用平行四边形的特征,PB′=BD,两点之间线段最短,故AB′距离最短,也就是BD+AP最短,故可确定桥要建在PD处.
三、代数法
数学知识范畴广泛,代数和几何是数学课程体系的两大构成部分,对于初中数学几何问题而言,还可以运用代数法突破难点.在当前教育背景下,新课标对初中数学中几何知识的要求是:让学生理解图形,淡化概念识记、套用公式的做题模式,深化数学定理理解,从而灵活应用概念知识,做到几何问题的建模与求解.在初中数学几何问题解题教学中,学生需要经过学习建立“大数学”观,发散思维,学会合理使用代数知识突破解题瓶颈.所以,在日常教学过程中,教师可传授将特殊几何问题转为代数问题的方法、技巧和思路,从而简化计算,帮助学生获得更明晰的推理逻辑与证明思路,在解答几何问题的过程中培养学生的创新思维,依托于知识间的联系强化学生的整体解题能力.
四、逆向思维法
证明题在初中几何问题中的占比较大,是一种十分常见的题型,相较于计算类的几何问题,证明类几何问题对学生的推理能力具有较高要求,其中,推理包括正向思维推理和逆向思维推理.在一些题目中,正向思维推理可能较为复杂,推理步骤也相对较多,即便学生可以通过这一思路完成,花费的解题时间也较长,所以,教师可以引导学生使用逆向思维解答几何证明题.逆向思维法的本质在于:从与题干中要证明的结论对立的结论展开,证明其与命题矛盾,即可说明要证明的结论成立.
例4 如图4所示,圆O中有AB,CD两条弦,均不是直径,请证明AB与CD不能相互平分.
在该几何问题中,根据题干内容学生很难在短时间内找到证明思路,所以,可从结论出发,即:假设AB与CD能够相互平分,接着推理、求证,利用与现有定理的冲突,借助逆向思维证明此题.解题思路与技巧为:设弦AB和弦CD的交点为点P,连接OP,假设两条弦能够相互平分,这意味着AP=BP,CP=DP,而弦AB与弦CD是圆O内两条非直径的弦,故OP垂直于CD,OP垂直于AB.这与“过一点有且只有一条直线同已知直线垂直”相悖,故假设不成立,证明弦AB与弦CD不能相互平分.
五、建系法
当学生接触几何问题时,其已经具备平面直角坐标系相关知识,也掌握了点、线、面等相关定理与公式,初步具备了在平面直角坐标系中处理数学问题的基本能力.在解答几何问题时,教师可引导学生精准应用建系法突破解题障碍,尤其是一些单纯使用几何知识与方法较难求解的情况,可组织学生提炼题干信息,以此为基础进行平面直角坐标系的构建,通过结合点的坐标转化问题形式,降低问题难度,提高问题解答效率.
例5 如图5(a),四边形ABCD与四边形CGEF均为正方形,前者边长为2,后者边长为3,点B,C,G位于同一条直线上,点M为AE中点,连接MF,求MF的值.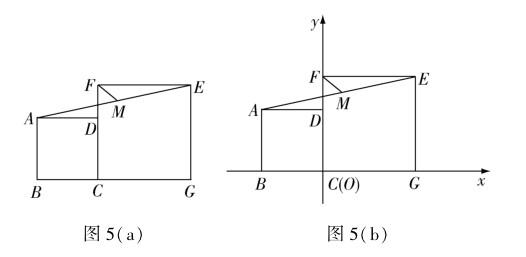
运用建系法解决此道几何问题时,首先要对题干进行分析.根据题干内容发现,单凭几何知识无法解决这一问题,所以可在图5(a)的基础上建立直角坐标系,建立情况如图5(b)所示.
结 语
综上所述,为提高初中生解决几何问题的效率,提升其数学学习自信心,教师可围绕常见几何题型,总结、传授辅助线法、平移法、代数法、逆向思维法、建系法等解题技巧,锻炼学生的几何问题思维,培养他们的空间想象能力,以及数学知识的灵活运用能力等,以实现解题技巧的精准、有效运用,提高学生整体解题实力.
【参考文献】
[1]王琪琼.借助多元解题技巧,突破初中数学几何题解题障碍[J].数理天地(初中版),2023(19):30-32.
[2]刘亚萍.辅助线在初中几何解题中的应用与技巧[J].考试周刊,2020(39):80-81.
[3]朱清波,王海青.基于变式理论的数学习题课教学模式探究:以一道解析几何问题的解决为例[J].数学通报,2022,61(8):50-54.
[4]李洁.基于几何推理能力的初中数学教学策略探究:以初中“手拉手模型”几何专题复习为例[J].数学教学通讯,2021(23):46-48.
[5]陈刚.小题大做思路尽显:初中数学一道几何题的多种解题方法[J].中学生数理化(教与学),2020(2):83,85.
[6]张昆.发展数学核心素养的教学设计研究:从“推理意识”过渡到“推理能力”的视点[J].中小学教师培训,2021(10):39-43.
[7]胡军,严丽.核心素养导向下初中生数学高阶思维发展路径[J].中小学教师培训,2020(10):67-70.
[8]杜晓婷.聚焦学科核心素养提升数学运算能力:基于数学核心素养的初中“数与代数”教学实践探索[J].中学教学参考,2020(11):8-9.
[9]谢翠兰.核心素养导向下初中数学课堂上的师生互动:以苏科版“探索三角形全等的条件”的教学为例[J].数学教学通讯,2022(26):41-42,48.

