GeoGebra软件在高中数学教学中的有效应用

曹欣楠 郑惠 徐孟竹

摘  要：课程改革逐步深化，要求强化学生数形结合、数学建模等数学思维及能力，信息技术与课堂教学有效结合的重要性逐渐凸显.其中，GeoGebra作为一款动态数学软件广泛应用于高中数学教学，可以在圆锥曲线等相关问题中，辅助学生将模糊抽象的知识内容通过直观观察，发现其数量与图形间关系.

关键词：GeoGebra；圆锥曲线；数学教学

随着新课程、新高考、新教材的不断推进，信息技术的变革已经更加深入地融合进高中的数学课堂，传统高中数学教学过程中单一乏味的灌输式教学模式正在信息化改革中逐渐生动，并为学生主动参与提供有效方法及途径.学生在参与探究的过程中，简化复杂问题，具化抽象知识，增强学习效果.GeoGebra作为新教材推荐使用的数学应用软件，与我们所熟知的几何画板相比，在保持数学知识生动形象优势的同时，其各类功能的操作更加直观、便捷，数据与图形间的变化关系也更为突出.可以有效调动学生探索数学建模的意识，并解决数学相关学习中问题的积极性，挖掘学生创新思维意识，营造良好的数学学习氛围.［1］

通过对近年高考试题的统计可以发现，圆锥曲线作为高考考查的重点内容，平均分值约占高考试卷

总分

的14.6%.圆锥曲线的命题类型稳定在“两小一大”，且在高中阶段圆锥曲线内容的学习，可以帮助学生建构一定的知识体系，有助于学生数学核心素养以及数形结合思想的培养.基于此，笔者将以圆锥曲线的相关内容作为研究对象，以实际教学内容为案例浅谈如何在GeoGebra软件的帮助下高效率完成数学教学.

1  圆锥曲线的生成

传统教学中教师往往喜欢将椭圆、双曲线以及抛物线的生成与实物相结合，从生活中常见的实物或景观出发，如常见的椭圆有盘子、西瓜、航天器运行轨道等；双曲线有发电厂通风、冷却塔、广州“小蛮腰”等；抛物线有石拱桥、篮球的抛物运行轨迹等.不同类型的圆锥曲线的生成过程意在引导学生将数学知识生活化，为学生创造熟悉的数学知识形象.但学生对圆锥曲线的由来还有些陌生，在此问题基础上，教师通过GeoGebra软件为学生进行动态演示，引导学生通过观察变化过程，探索圆锥曲线的生成.借助有关变量的数据变化所引发的截面图形的变化（如图1），可以极大程度促进学生对圆锥曲线由来的有效理解.［2］

点评：在教师的以上操作下，通过切割平面以及角度的变化，学生能够发现，用不同角度的平面来切割圆锥，所产生的曲线形态不同，因此将其衍生出来的椭圆、双曲线以及抛物线命名为“圆锥曲线”.此时，通过GeoGebra软件以最直观的方式帮助学生建立圆锥曲线的相关认识，也为逐一突破三种曲线相关问题做好铺垫.

同时，在“椭圆、双曲线以及抛物线的定义”这一

节

内容的学习过程中，其实际作图过程也是在探索各曲线上动点所满足相应条件的过程，加深学生对圆锥曲线定义的理解.

在以往椭圆的实际教学过程中，教师会引导学生通过细绳实验，在定义条件下完成椭圆轨迹的建构，操作时间较长，会对教学进度产生一定影响，新课改当下，教师可以通过GeoGebra软件中智能绘图工具代替定长细绳，在定义条件下模拟实际实验中的操作步骤，生成动点轨迹，如图2所示.

接下来将以抛物线的形成过程为例，详细阐述借助GeoGebra软件生成抛物线的实际操作过程：

步骤1：通过点与直线工具直接生成定点F以及直线l，注意此时点不在线上，当系统生成标签与定义描述条件不同时也可通过右键中的设置进行修改.

步骤2：通过点工具选取直线l上任一动点M，借助线段连接MF，并通过中垂线工具生成垂线h.

步骤3：过动点M借助垂线工具生成过点M的垂线交直线h于点P.

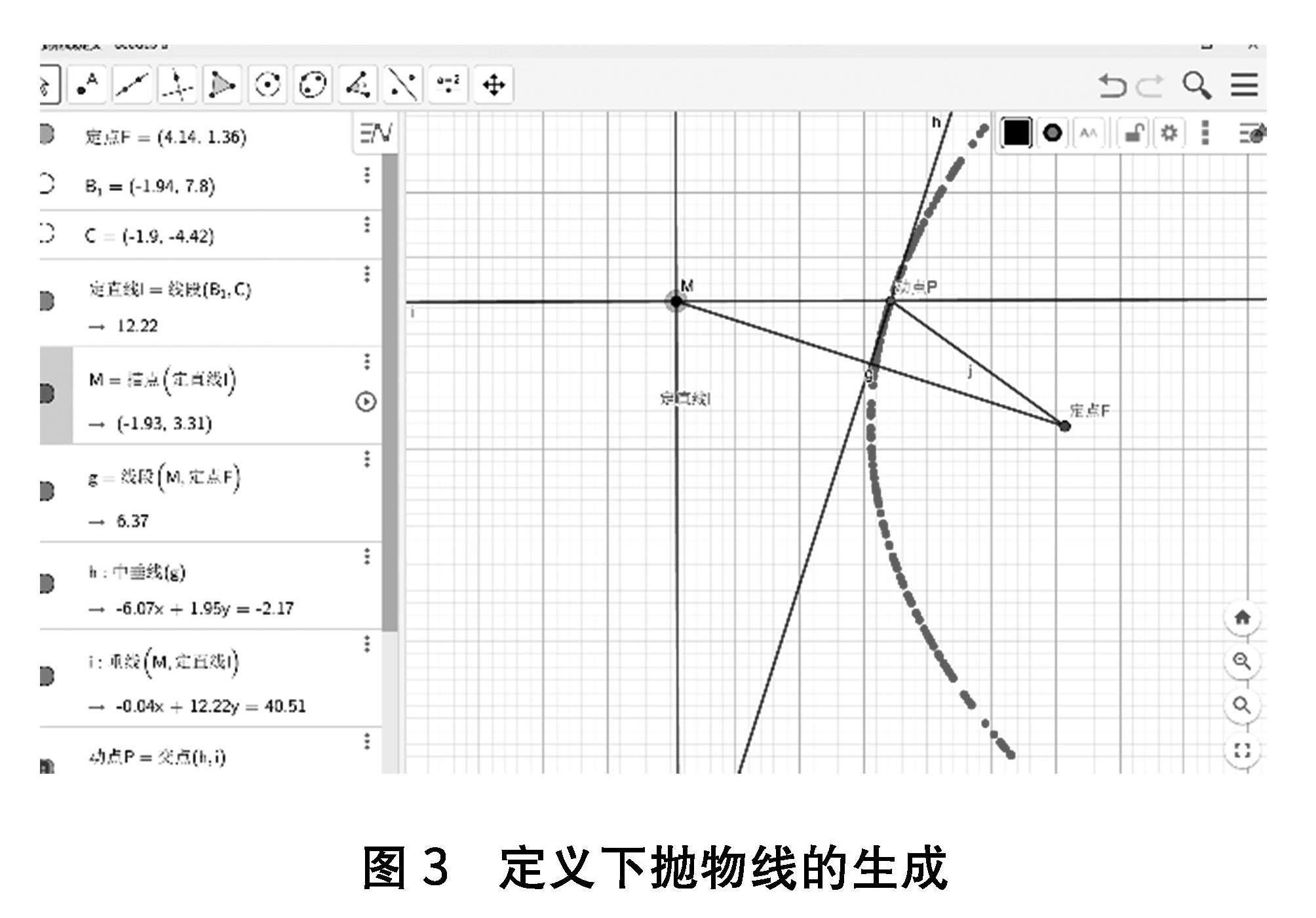
步骤4：右键显示点P运动轨迹（如图3），并在对动点P的移动过程中，观察生成动点P的轨迹即为抛物线.

点评：相较于椭圆，抛物线在实际教学中教师板演生图的过程操作起来更为复杂，成功率不高，且点与直线方向不易更改，而借助GeoGebra生成的抛物线图形，既可以通过拖动点改变与直线的距离观察抛物线开口大小的变化，也可以通过对直线方向的改变，快速生成四种开口方向的抛物线曲线，为接下来探究抛物线的四种标准方程作准备，对延伸教学起着重要的作用.

2  直线与圆锥曲线公共点个数问题

在实际教学过程中以椭圆为先导研究该类问题时，学生能够自主意识到借助联立思想，通过对方程中实数解个数的判断解决相关问题，并判断此时直线与椭圆的位置关系.但直线与其他圆锥曲线只有一个公共点时，需提醒学生，并不代表一定相切，也可能存在相交的位置关系.比如抛物线y2=2x与y=1这类平行于对称轴的直线，此时我们称直线与抛物线相交.常见的双曲线中与渐近线具有平行位置关系的直线，同样仅有一个公共点且相交.接下来以下题为例进行实际教学的讲评.

例题1  已知直线l：y=kx-1与双曲线C：x2-y2=4，讨论k的不同取值下，直线l与双曲线的公共點个数关系.

探究1  从“数”的角度研究，在教学中可以发现学生在见到此类问题的首选方式往往是联立方程，由y=kx-1，

x2-y2=4，

得（1-k2）x2+2kx-5=0.

当1-k2=0，即k=±1时，直线l：y=±x-1与渐近线y=±x平行，公共点有且仅有1个.

当1-k2≠0时，若Δ=0，解得k=±52.

此时直线l与双曲线相切，公共点仅有一个；

若Δ>0，解得-52

此时直线l与双曲线相交，公共点有两个.

若Δ<0，解得k<-52或k>52时.

此时直线l与双曲线相离，不具有公共点.

但学生在运算过程中极易忽略对二次项系数的讨论，实际教学过程中可在学生产生遗漏后进行引导补充，加强学生对细节的观察与探究能力的培养.

探究2  从“形”的角度研究，教师在多媒体设备及GeoGebra软件辅助下作图4.

通过参数的连续变换，直观观察图形间关系的变化，能够帮助学生突破对直线与双曲线的公共点个数问题的理解，提高教学效率.并可以通过对定点的移动，将问题进行变式：将直线l分别变为y=kx-12、y=k（x-2），并在课堂中予以时间进行训练，帮助学生突破此类问题的多种情况，真正理解直线与圆锥曲线问题的内涵与外延.同时也将信息技术与数学课堂完美结合，有效地激发学生的学习热情与探索精神，培养学生逻辑推理及数学运算等核心素养.

3  圆锥曲线中的定值与定点问题

定值定点问题是高考中圆锥曲线中的常规热点问题，在培养学生对代数条件与几何关系的理解下，提高其数形结合意识，也是对学生计算能力的考查，同时侧重训练学生综合调动各模块知识的能力，综合性较强，加之此类问题的计算量通常较大，费时费力难以攻破.通过对近几年的高考试题的统计可以发现，定值定点问题的常用方法可以总结为：①直接求解；②先猜后證.［3］“直接求解”也就是我们通常所说的参数法，

分为以下步骤：

①根据题设引入参数；②由已知整理出含参关系式；③化简，并进行求解.“先猜后证”即从特殊到一般：①从问题的特殊情况出发，如斜率不存在或横截距式中斜率为零等，得到目标关系所要探求的定值或定点；②探究一般情况；③定结论，综合以上两种情况确定结论.

在这类问题学习的初始阶段，为了帮助学生理解数量关系，教师需要根据已知题设条件，建立目标图形，帮助学生建立数学结合的思维，不妨以下面两道题为例来进行讲解.

例题2  已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过A（0，-2），B32，-1两点.

（1）求

椭圆

E的方程；

（2）设过点P（1，-2）的直线交椭圆E于M，N两点，过点M且平行于x轴的直线与线段AB交于点T，点H满足MT=TH，证明：直线HN过定点.

该问题选自2022年全国乙卷，第（2）小问即考查解析几何章节中圆锥曲线中动直线过“定点”的问题.

步骤1：根据（1）的计算结果在命令输入区直接输入椭圆方程y24+x23=1及点P（1，-2）.

点评：传统几何画板中椭圆等曲线的绘制较为复杂，且当方程变化后往往需要重新绘制，增加教师备课工作量，而GeoGebra软件在处理解析几何等问题中的快捷、高效性主要体现在方程与图形的直接联系，仅需根据输入所需曲线方程即可自动生成相应图形.若方程发生变化，也可以通过直接更换数值或设置滑动条，通过拖动滑动条观察参数在变化过程中曲线的变化情况及其他相关点的变化情况.

步骤2：直线工具绘制过点P的直线交椭圆于M、N两点，利用平行线工具做出过点M且平行于x轴的直线，找到点T.

步骤3：借助功能区的相等向量关系构造相等关系，确定点H

的

位置从而确定直线HN.

图5  定点问题实例示意图

探究1  右键显示直线HN踪迹，通过拖动改变图形关系中控制点M的位置，即改变过点P的直线的斜率，此时可以发现直线HN变化过程中恒过定点，进一步观察可以发现其定点恰为A（0，-2），并通过计算，可以验证该结论.

点评：解析几何，顾名思义借助解析式进行图形研究，在GeoGebra软件的帮助下所直接呈现的直线与曲线的同步变化关系可以更加方便我们探知问题的本源，从多角度，更深层次理解问题，甚至直接观察到预想结果，确定问题研究的目标及方向.一方面帮助学生在积极的课堂环境及探索氛围下提升数学感知能力，培养数与形的结合意识；另一方面，图形的建立也是在帮助学生化繁为简，将较为抽象的问题具体化，从而达到理清思路，优化条件的目的.在对图形的变化进行观察并掌握变化规律后，教师在教学过程中还要引导学生从代数角度对观察到的结果进行检验，得出准确结论.

探究2  拖动控制点M的过程中也可以发现，当过点P的直线斜率不存在时，即直线MN垂直于x轴时，直线HN仍过点A，进一步验证了恒过定点A（0，-2）这一结论.

点评：特殊情况作为研究问题的重要研究思路，往往可以揭露问题的本质，通过对斜率是否存在的讨论探究，从特殊到一般或从一般到特殊也是解决解析几何定值定点问题的重要数学方法，通过图形的变化，以最直观的方式引导学生解题方向，完善教学内容，改善教学方式.

接下来，在同类定值问题的教学过程中，教师也可以通过运用GeoGebra这一动态数学软件，在与学生共同审题探究的过程中，将条件逐一构建完成，帮助学生确定目标结果，以下题为例.

例题3  已知椭圆C：x2a2+y2b2=1（a、b>0）的离心率为12，并过点P（0，3）.

（1）求椭圆C的方程；

（2）设过点P的直线与x轴交于点N，与椭圆的另一个交点为B，点B关于x轴的对称点为B′，直线PB′交x轴于点M，求证：｜OM｜·｜ON｜为定值.

该问题（2）考查圆锥曲线问题中动直线条件下的“定值”问题.

步骤1：学生经过计算后，输入（1）中得到的椭圆C的方程：x24+y23=1，运用点工具确定点P，并通过直线工具选定点P及x轴上任一点N；

步骤2：通过交点工具选定直线与椭圆，自动生成交点B，轴对称工具选定对象B及对称轴x轴，此时系统自动生成对称点B′且在椭圆上；

步骤3：直线工具选定点P及点B′，点工具确定与x轴交点M，线段工具连接OM与ON，完成题干的准备工作；

步骤4：令a=｜OM｜，b=｜ON｜，c=ab，通过移动点N，观察过点P的直线的斜率在变化过程中，a、b、c数值的变化，如图6，可以发现c=｜OM｜｜ON｜=4恒成立.

点评：总的来说，定值定点问题作为圆锥曲线的重点内容，通过信息化软件与多媒体设备的结合，借助图象准确地对问题条件中所涉及的点、线（包括曲线）进行描述，可以在提高數学教学效率的同时，培养学生信息化意识，帮助学生节省将新内容、新知识内化为自身数学知识结构所消耗的大量时间.而GeoGebra软件的最大优势就在于它工具中所涵盖功能的多元化、全面化，无论是高中数学学习中所涉及的代数问题、几何问题还是统计问题均可使用，这又在极大程度上减轻了部分对画图软件不熟悉的教师在备课过程中的负担.

高中数学教学的成功与否不是让教师灌输式地将知识原封不等的传授出去，而是要帮助学生尝试建构并完善自己的知识体系，最终实现自主学习能力的培养.通过以上三种类型的具体教学案例可以发现，解决圆锥曲线这一章节的内容本质是对学生逻辑推理能力的考查，学生要具备通过推理完成几何语言的解读，将数量关系与图形关系相结合，在准确表述的前提下，明确问题所采用的运算方法，完善解题过程，优化对解析几何问题算法构建的理解.在2017版《普通高中数学课程标准》中明确提出，在平面解析几何的教学中，“应充分发挥信息技术的作用，通过计算机软件向学生演示方程中参数的变化对方程所表示的曲线的影响，使学生进一步理解曲线与方程的关系”.而GeoGebra软件作为高中数学教师教学与学生学习的认知工具，能够将数学的抽象知识变得具体化、形象化，提高教学效率，同时对学生直观想象、数学抽象等数学核心素养的培养也有着一定的提升作用，为教师改善高中数学传统教学模式提供多元化思路.

参考文献

［1］李琨.GeoGebra软件在高中数学课堂中的应用——以“圆锥曲线”教学为例［J］.数学教学通讯，2022（27）：25-26.

［2］陈锋，沈才权.GeoGebra在高中数学单元教学中的应用探微——以《圆锥曲线的方程》为例［J］.试题与研究，2022（18）：36-38.

［3］张志勇.GeoGebra软件在高中数学教学中的应用举例［J］.福建中学数学，2014（4）：6-9.