“倍”的课程价值及其学习活动设计

齐美 郜舒竹

【摘   要】“倍”这一概念在小学数学课程中具有重要价值。它能够丰富学生早期的计数经验，为学生学习分数、比奠定基础，并帮助学生发展单位化的眼光。为此，可设计“用‘倍看关系”的学习活动，通过具身活动操作、个体经验联结、多元图式建构、关键概念辨析四个步骤，帮助学生主动建构倍的心理意义、理解倍的数学含义并形成多元化表征的能力。此外，为避免学生混淆“倍的认识”中的“倍”与“因数与倍数”中的“倍数”两个概念，还需对这两个概念的异同进行比较，以促进学生对“倍”和“倍数”的理解。

【关键词】倍的认识；学习活动；因数与倍数

本刊上一期刊登的《“倍”的意义不仅是除法运算的结果》一文指出，有关“倍的认识”的教学存在意义不完善的问题，即将“倍”仅仅理解为除法运算的结果。事实上，“倍”还可以用于描述关系。在此基础上，本文进一步分析“倍”的课程价值，探究如何在数学课程设计与实施中落实“倍是关系”的意义，并让学生在具身活动中，借助隐喻思维体会“倍是关系”。但在这一过程中，学生会遇到一些认识上的障碍，易于混淆“倍的认识”中的“倍”与“因数与倍数”中的“倍数”两个概念。为此，需要对这两个概念的异同进行比较，以避免概念上的混淆。

一、“倍”的课程价值

“倍”是表达量与量、数与数之间关系的语言。这种抽象的理解需要依赖隐喻。隐喻不仅仅是一种语言现象，还是人类理解周围世界的一种感知和形成概念的工具［1］。乔治·莱考夫在《数学从哪里来》一书中提到：人类天生具有内含的算术能力，包括识别少量物体数量的计数能力和进行简单加减的运算能力。不过，当物体数量大于4时，人类随之需要发展组合分组能力与符号表征能力。而若想全面掌握数的运算及其属性，就需要提升隐喻能力（Metaphorizing Capacity）以及概念融合能力（Conceptual-blending Capacity）等认知能力。［2］这表明概念隐喻和概念融合是人类最基本的认知机制之一，它们共同促进了人类从先天算术能力发展到自然数的基本算术能力的进化。

在数学认知中，数可被视为一组对象所形成集合的隐喻，即一种从物理对象领域到数字领域的精确映射。因此，“5和7哪个大”和“2比4小”此类表达在人的头脑中根深蒂固。可实际上，数本身并无大小之分，人无法直接看见数的具体存在。比如，当学生在现实世界看到图1所示的小方块时，他们就会在头脑中形成6的概念，表示这些小方块的总数量是6个。

然而，隐喻的过程并不是一成不变的。即使是相同数量的对象，也会因为使用的映射方式不同，而在头脑中形成不同的数。比如，当学生看到图2所示的小方块时，他们可能会无意识地对其进行分组，将2个小方块视为一个单位。此时，他们的意识中便会浮现3。这里的3表示有3组，每组包含2个小方块。这表明“倍表示关系”以隐喻的方式存在于学生早期的计数阶段，并丰富了他们的计数经验。

学生在系统学习“倍表示关系”时，会认识三种意象图式（Image Schema），即比较图式、部分—整体图式和变化图式，分别对应用“倍”描述的三种不同关系：不同对象之间的关系、部分与整体的关系和变化前后的关系。这三种意象图式在后续分数和比的学习中也有所体现，为学生进一步学习分数和比奠定了基础。

首先是比较图式。分数和比都具有描述不同对象之间关系的功能。以图3为例，用分数的语言来说，第一行小方块的数量是第二行小方块数量的[12]。用比来描述，则可以说第一行小方块与第二行小方块的数量之比为1∶2。

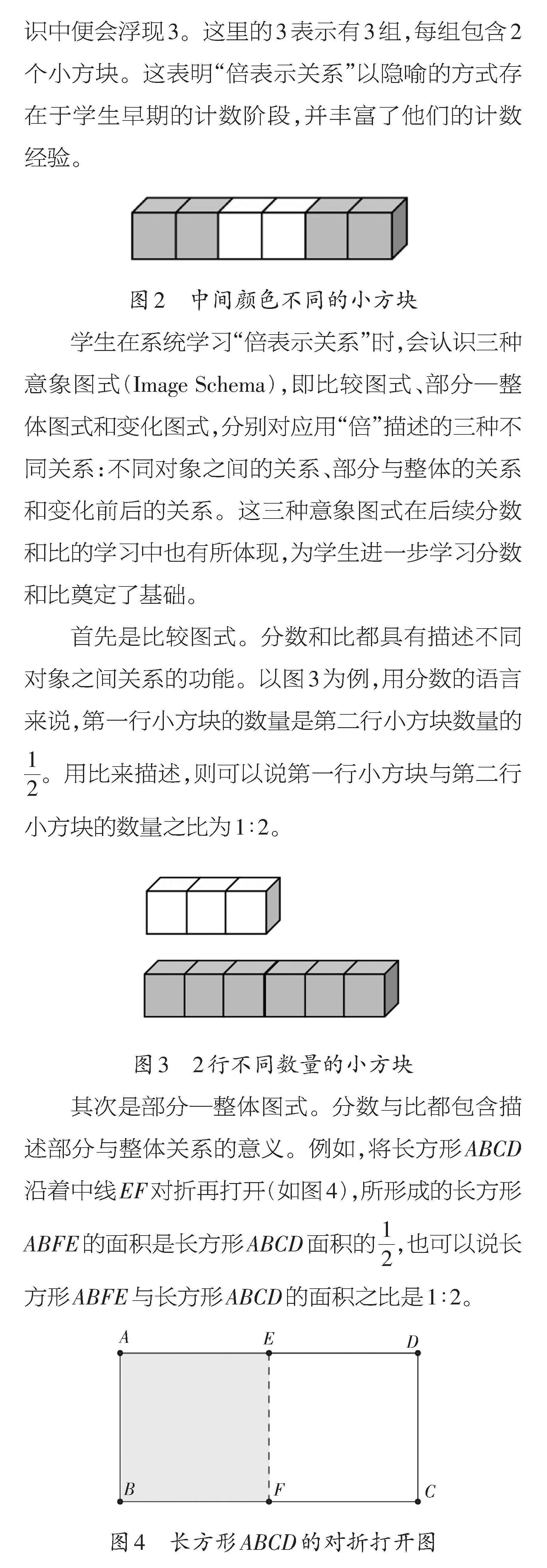
其次是部分—整体图式。分数与比都包含描述部分与整体关系的意义。例如，将长方形ABCD沿着中线EF对折再打开（如图4），所形成的长方形ABFE的面积是长方形ABCD面积的[12]，也可以说长方形ABFE与长方形ABCD的面积之比是1∶2。

[A][E][D][C][F][B]

图4 长方形ABCD的對折打开图

最后是变化图式。分数与比在变化图式的应用上有所不同。先看分数，假设一个月前，树苗A高8分米，树苗B高12分米。现在它们的高度分别是11分米和15分米。请问：哪株树苗长得快？用加法来推理，可以得出两株树苗都长高了3分米，因此长得一样快。而用乘法来推理，得出的结果却是树苗A长得更快。这是因为与原先的高度相比，树苗A长高了[38]，树苗B长高了[312]，[38]大于[312]，所以树苗A长得更快。再看比，变化图式在比例问题上体现为表征形式的相似。例如，将一个保温杯缩小为原来的一半画在纸张上，那么在原始图像中相等的东西，在新建立的图像中也应该相等。这意味着从原始图像到新建立图像的映射过程描述为相似性，但图像元素中内部结构的比不变。［3］

除了能为学生学习分数和比奠定基础，倍的学习还能帮助学生发展单位化的眼光。杜威在《数的心理学》中提到：数被简单定义为多少个度量单位（Units of Measurement），往往是抽象的［4］。可见，表示一个量数值的数与度量单位和重复次数密不可分。从离散的角度来看，数是许多个度量单位所构成的统一体；从抽象的角度来看，数则是一个度量单位所形成的局部。例如，50元既可以看成是由50个1元组成的，也可以直接看作一个度量单位。用倍的语言来说就是：50元是1元的50倍，或者50元的1倍。当然，50还可以由其他不同的组合方式组成，如2个25、5个10、10个5等。选择的度量单位不同，度量的方式也不同。

综观学生从整数到分数、小数再到无理数的数概念学习过程，倍、分数、比这三个概念密切相关。以乘法比较的相关问题为例，在倍的学习中，通常将较小量看作单一量（标准量），与较大量进行比较。而在分数的学习中，通常将较大量看作单位“1”（标准量），与较小量进行比较。这两种方式分别用“一个数是另一个数的多少倍？”和“一个数是另一个数的几分之几？”来表述。例如，如果短木棒长10厘米，长木棒长15厘米，那么既可以说长木棒的长度是短木棒长度的1.5倍，也可以说短木棒的长度是长木棒长度的[23]。此外，“倍”还是理解“比”的重要基础，因此可以用组合单位的方式来理解比。比如：如果4颗蓝莓的价格是1元，那么这4颗蓝莓就可以看作一个单位。基于这个单位可以推导出其他倍数成立的情况，如8颗蓝莓2元、40颗蓝莓10元等。同时，也可以将单位进行缩小运算，得出2颗蓝莓为0.5元、1颗蓝莓为0.25元。也就是说，任何数量的蓝莓都可以通过使用这些组合的单位来定价。

综上所述，“倍”这一概念在小学数学课程中具有重要价值。它不仅能够丰富学生早期的计数经验，为学生进一步学习分数和比奠定基础，还能帮助学生发展单位化的眼光。因此，如何设计相关的学习活动，以促进学生理解“倍”这一概念就显得尤为重要。

二、“用‘倍看关系”的学习活动设计

学习活动是学生通过自我理解、生生互动、师生交流实现变教为学的一种方式。从多元表征的认知功能来看，设计学习活动的意义在于整合各种表征的优势与特点，形成更为完善的内在表征结构。而精心设计多元表征的学习活动，能够帮助学生深入理解并内化多元表征，生成整个表征结构，并学会建构多元表征的策略与方法等。［5］

人的认知是在其心智、身体与环境互动的过程中，无意识形成的具有稳定性的思维方式。这种思维方式会不自觉地支配人们的行为，兼具“意象”和“图式”的意义。［6］作为一个抽象数学概念，学生对“倍”的理解与掌握需要经历三个阶段：首先是现实世界中的具身操作，其次是思维世界中的具身经验积累，最后是符号世界的抽象表征。学生若要理解某个数学结构，就必须在这个数学结构与另一个更易理解的数学结构之间建立对应关系。而表征是建立意义、交流信息、促进理解的重要手段。［7］

“倍的认识”是人教版教材三年级上册的教学内容。教学时，教师可以按照具身活动操作、个体经验联结、多元图式建构、关键概念辨析四个步骤，帮助学生主动建构倍的心理意义、理解倍的数学含义，形成多元化表征的能力。

教学伊始，教师通过展示两组不同小方块学具之间的关系，激活学生已有的知识经验，如加、减法之间的关系，引出课题——用“倍”看关系。教学中，教师主要安排以下四个学习任务。

任务一：用学具摆出“2倍”关系

学具的拼摆是一种将抽象的数学概念“2倍”关系具体化的活动。在具身操作活动中，学生通过摸、摆、拼等方式，深入体会“2倍”关系的实质，从而形成对比不同对象的意象图式。这种具身体验使学生更容易理解和构建数量关系的模型。在这一过程中，学生经历用不同的对象表示“2倍”关系，体会“2倍”关系的表述既可以是“6个小方块是3个小方块的2倍”，也可以是“8个小方块是4个小方块的2倍”，以及更多类似的表述。但无论学具如何拼摆，其倍数关系都具有一个共同的特征，即内在的抽象性。可见，理解这种抽象概念需要依赖具体的、具有象征意义的操作。

任务二：结合自身经验，举例说明“2倍”关系

数学语言有助于提升学生的叙述性表征能力和逻辑推理能力。学生通过运用自身经验举例说明“2倍”关系，实现了新旧知识的整合与同化。在这一过程中，他们能够灵活运用倍数关系描述不同物体之间的数量关系，如“有两堆铅笔，4支铅笔是2支铅笔数量的2倍”“2塊粉橡皮是1块白橡皮数量的2倍”。这不仅有助于监测学生的学习成果，还能提升他们运用数学语言表达现实世界的能力。

任务三：通过折纸活动，找到“8倍”关系

教师先向学生示范将长方形纸张对折的过程，引导学生观察纸张对折过程中面积发生的变化，使学生初步理解“倍”表示部分与整体的关系。随后，让学生展开自主探究，自行尝试将一张长方形纸对折、对折、再对折。通过这样的三次对折，学生发现：整个长方形的面积分别是每次对折后小长方形面积的2倍、4倍、8倍。这一发现打破了学生的线性认知，使他们意识到纸张的对折过程并非简单的线性变化，而是涉及更复杂的非线性关系。从表征的感觉通道来说，折纸是一种动作表征，能激活学生头脑中关于倍数关系的认知，促进他们对这一知识的理解与应用。为此，可以引导学生继续对折纸张，让他们思考接下来会形成怎样的倍数关系，由此激发他们的求知欲和探索精神。

任务四：小组讨论“增加了2倍”与“增加为原来的2倍”的意思是否一样

任务四要求学生学习“倍”的另一种含义，即描述物体数量变化前后的关系，从而发展学生的数学眼光，使学生学会动态地看待倍数关系。通过小组讨论和辨析，学生体会到小方块“增加了2倍”与“增加为原来的2倍”这两种表达方式在意义上的差异。具体来说，“小方块增加了2倍”形成了新的标量关系。将初始状态下小方块的数量看作单一量，增加了2倍表明增加的量是单一量的2倍，那么结束状态下小方块的数量就是原来的3倍。这一变化后与变化前的增量，意义指向标量关系的动态改变。而意义又源于差异。［8］为此，要让学生在差异中进一步理解倍数关系的不同含义。

这四个任务不仅能帮助学生理解“倍”的含义并建构“倍”的意义，还能在整个数学学习过程中起到承上启下的作用，唤醒学生的已有经验，为学生后续学习分数、比等概念奠定基础。其中，任务一帮助学生理解不同对象之间的关系，是他们学习比的概念的重要基础，如宠物店里猫与狗的数量之比是3∶2、圆周长与直径之比为π∶1等。而这些比的概念又延伸出重要的数学推理方法——比例推理。利用比例推理，就能有效解决路程问题、比例尺问题、密度问题以及浓度问题等。［9］任务三着重引导学生理解部分与整体的关系，是建立分数概念的起点，旨在通过折纸活动，让学生更直观地理解分数的面积模型。此外，分数还涉及测量的意义。以分数[38]为例，它表示以分数[18]为单位长度，数出这样的3个单位长度，即3倍的[18]。按照这样的认识，学生明白了分数是单位分数的倍数，从而拓展了对分数的认知。任务四旨在引导学生思考如何解释加法推理和乘法推理的区别，以帮助学生更好地掌握加法比较和乘法比较之间的异同。综上所述，这四个任务不仅有助于学生对“倍”概念的理解与掌握，还能为他们后续的数学学习打下坚实基础。

三、“倍”与“倍数”异同比较

继学生在低年级学习“倍的认识”之后，教材又在五年级编排了“因数与倍数”的学习内容。由于学生先前已接触过“倍”的概念，因此在理解“因数与倍数”中的“倍数”时，他们会遇到一些认知障碍。所谓认知障碍，指的是概念本身所形成的障碍，也可以解释为错误的思维方式。学生的思维方式会影响学生对数学概念的理解方式，而这种理解方式又会反过来影响学生的思维方式。［10］因此，有必要对“因数与倍数”中的“倍数”与“倍的认识”中的“倍”的异同进行比较，以避免学生混淆这两个概念。

一方面，两个概念存在诸多差异。首先，两者所指的对象不同，“因数与倍数”中的“倍数”指的是用测量单位来测量的对象，而“倍的认识”中的“倍”指的是测量过程中进行的次数。例如，在看待12这个数时，12可以看作3个4或4个3，这里的3和4就是12的因数。同时，12也是3和4的倍数。因测量需同时具备测量的对象和测量的单位，所以因数和倍数是相互依存的。但在“倍的认识”中，“倍”描述的是测量单位和测量对象所形成的标量关系。［11］即12是3的“4倍”或4的“3倍”。

其次，两者的使用范围不同。“倍数”的使用范围仅限于正整数除法且除尽的情况，而“倍”的使用范围则更广，不仅包括整数倍，还包括小数倍和分数倍。在人教版教材五年级下册第二单元中，教材明确了两个整数相除后可能出现的两种情况，并据此给出了因数和倍数的定义：“在整数除法中，如果商是整数且没有余数（或者说余数为0），我们就说除数是被除数的因数，被除数是除数的倍数。”例如，在12÷2=6这种情况下，12是2和6的倍数，2和6是12的因数。也可以说12是2的6倍或6的2倍。然而，在9÷5=1……4这种情况下，由于商不为整数，因此9和5之间并不构成因数与倍数的关系。不过，当9÷5=1.8时，说9是5的1.8倍，这种表述依然是符合数学逻辑的。

最后，两者所延伸出的概念也不同。“倍数”可以进一步延伸出公倍数、最小公倍数等概念，而“倍”延伸出的概念则与比的概念紧密相连，如正方形的对角线与边长之比是[2]∶1。在此基础上，“比”的学习又为之后中学要学习的斜率、三角函数、相似等知识打下重要基础。

另一方面，两个概念间也存在一些共同点。首先，无论是“倍”还是“倍数”，它们的形成都离不开测量对象和测量单位。倍数和因数相互依存，“倍”连接倍数与因数，这两个概念都不能独立存在。不能说12是倍数，必须描述清楚12是3的倍数或者12是3的4倍。其次，两者名称相似，如果不加以区分，对于没有学习过“倍数”概念的学生来说，极可能认为这与“倍”是同一个概念，从而造成认知障碍。最后，算式的呈现方式相同，两个概念都可以使用除法或乘法算式来表达。比如，描述12是3的倍数时，可以用除法算式12÷3=4或者乘法算式3×4=12来表达。描述12是3的4倍时，同样可以用除法算式12÷3=4或者乘法算式3×4=12来表达。

综上所述，通过对“倍”的课程价值分析、“用‘倍看关系”的学习活动设计以及“倍”与“倍数”概念的异同比较，可进一步加深学生对“倍”的理解。“倍”不仅连接了观察对象之间的关系，也发展了学生单位化的眼光。學生在关系中发展单位化的眼光，又用单位化的眼光理解关系，满足了他们用数学眼光观察现实世界、提升自身核心素养的要求。

参考文献：

［1］束定芳.隐喻学研究［M］.上海：上海外语教育出版社，2000：30.

［2］LAKOFF G，N??EZ R E. Where math-

ematics comes from［M］. New York：Basic Books，2000：51-52.

［3］FREUDENTHAL H. Didactical phenomenology of mathematical structures［M］. New York：Kluwer Academic Publishers，2002：189.

［4］MCLELLAN J A，DEWEY J. The psych-

ology of number and its applications to methods of teaching arithmetic［M］. New York：D.Appleton and Company，1909：96.

［5］唐剑岚.数学多元表征学习的认知模型及教学研究［D］.南京：南京师范大学，2008：28.

［6］郜舒竹，于桓.数学课程内容的抽象性及其隐喻思维分析［J］.课程·教材·教法，2022，42（1）：98-103.

［7］SCHULTZ J E，WATERS M. Discuss with your colleagues：why representations？［J］. The Math-

ematics Teacher，2000，93（6）：448-453.

［8］MARTON F. Necessary conditions of learning［M］. New York：Routledge，2014：48.

［9］CRAMER K，POST T，GRAEBER A O. Connecting research to teaching：proportional reasoning［J］. The Mathematics Teacher，1993，86（5）：404-407.

［10］BROWN S A. Exploring epistemological obstacles to the development of mathematics induction［C］// The 11th conference for research on undergraduate mathematics education，2008：1-19.

［11］WALLACE A H，GURGANUS S P. Teaching for mastery of multiplication［J］. Teaching Children Mathematics，2005，12（1）：26-33.

（首都师范大学初等教育学院）