基于算理算法一致性的“除数是两位数的除法”单元整体教学重构

周琪 沈彩虹 周小芳

【摘   要】凸显数学课程的整体性和一致性是发展学生核心素养的基本前提。现行教材尚未很好地体现数的概念与运算的一致性。教师在原有单元教学目标的基础上，抓住“计数单位”这一核心要素，提炼除法的本质就是“计数单位的细分”这一“理”，并利用乘除法关系，提炼“做除法想乘法”这一“法”，尝试用算理统领算法，从而贯通理法，落实运算的一致性。又根据调整后的单元教学目标，将整个单元重构为“口算除法”“初识算理”“巩固算理，形成算法”“总结算法”“优化算法”和“实现贯通”6个课时，打通算理和算法之间的壁垒，实现整数除法算理算法的一致性，促进学生对数学本质的理解，使学生形成结构化思维，为整数除法的贯通和小数除法的学习打好基础，发展学生的数学核心素养。

【关键词】整数除法；单元整体教学；算理算法的一致性

一、问题提出

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）倡导课程内容结构化整合的理念［1］。以整数除法为例，现行小学数学教材中，“除数是两位数的除法”是小学阶段整数除法最后学习的内容。在此之前，教材已系统地编排了与整数除法相关的大部分知识和技能，包括除法的意义、用乘法口诀求商、除法运算（口算与笔算）、竖式的书写格式、余数与除数的关系等。在此基础上编排“除数是两位数的除法”的学习内容，既承接了多位数乘两位数、除数是一位数的除法的学习，又为后续小数除法的学习奠定基础。进一步梳理、分析教材编排可以发现，贯通三个年级的整数除法学习存在共性：一方面，情境和意义是一致的，均为基于平均分的“计数单位”细分；另一方面，乘法与除法的关系也是一致的，即除法是乘法的逆运算，也就是做除法想乘法。这表明整数除法在算理和算法上都具有一致性。因此，将这一阶段的除法进行整体化教学，有助于学生构建完整的知识网络，并帮助学生理解整数除法的内在逻辑关系，以实现整数除法运算的一致性。

然而，现行教材在“除数是两位数的除法”单元教学目标的制订上存在以下问题：一是重法轻理，强调计算的方法，过于注重繁杂的技能，从而忽略了计算的“道理”；二是理不入法，缺少方法的统领，学习步子较小，用多个课时训练计算技巧，却未凸显除法运算的一致性；三是与原有知识的关联性不足，未能让整数除法的算理和算法系统化，缺乏一致性［2］。因此，有必要重新构建整体的知识网络，突出算理，总结算法，由算理统领算法，运用类比迁移的思想方法，突出知识和结构上的整体性和一致性［3］。

在2022年版课标发布但新教材尚未出版的过渡阶段，教师如何准确把握“除数是两位数的除法”这一单元的内容，帮助学生理解算理、巩固算法，实现理法的贯通，并感悟整数除法运算的一致性，为后续小数除法、分数除法的学习打好基础，是落实2022年版课标的课程理念的关键。本研究将基于“数的运算的一致性”，尝试对该单元的内容和结构进行整合与优化。

二、重构：单元整体教学再设计

（一）单元教学目标重构

在原有单元教学目标的基础上，抓住“计数单位”这一核心要素，提炼除法的本质就是“计数单位的细分”这一“理”，并利用乘除法关系，提炼“做除法想乘法”这一“法”，尝试用算理统领算法，据此对单元教学目标进行调整，具体如表1所示。

重构后的单元教学目标，其主要变化体现在以下两个方面：一是关于口算与笔算的算法，新目标突出乘法口诀的作用，即统一了“法”；二是在理解算理、探究算法并有效关联旧知的过程中，新目标强调除法运算是将计数单位逐步细分的过程，以此感受除法运算的内在一致性，即凸显了“理”。由此，在算理算法的自主探究与沟通中，发展学生的运算能力和推理意识。可见，重构后的单元教学目标更加精练地强调了算理算法的一致性，突出了算理在教学中的重要性。

（二）单元教学课时重构

根据调整后的单元教学目标，将整个单元重构为“口算除法”“初识算理”“巩固算理，形成算法”“总结算法”“优化算法”和“实现贯通”6个课时，每课时的主要内容和教学目标如图1所示。

此单元教学课时的重构将算理算法的一致性贯穿始终，强调除法的算理为“计数单位细分”，算法为“做除法想乘法”，并基于“先讲算理，后识算法，理法贯通，承前启后”的原则，开展阶梯式教学，最终实现算理算法的一致性。

（三）各课时关键任务设计

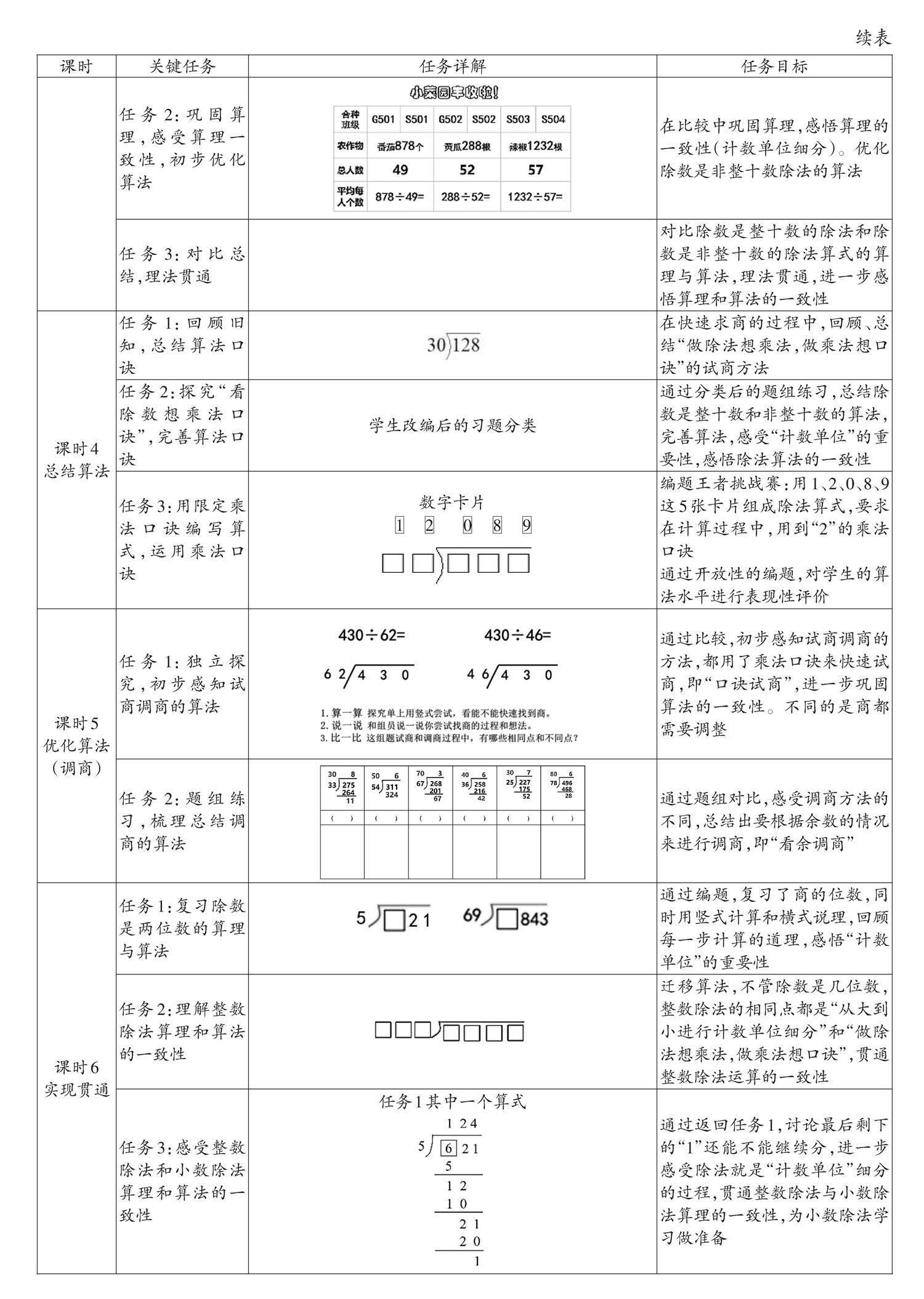
本次单元教学重构旨在帮助学生先理解除法的本质是“计数单位细分”，再优化除法运算的方法，最后贯通理法，感受整数除法运算的一致性。各课时的关键任务如表2所示。

从各课时的关键任务来看，试商等技巧并非笔算教学的重点，帮助学生理解试商的“道理”才是解决笔算难点的“通法”。因此，本次单元教学的重构将重点放在理解算理上，让学生在理解算理的同时掌握算法，从而打通算理和算法之间的壁垒，实现整数除法算理算法的一致性。在安排课时时，也尽可能地把时间用于教学解决一般问题的“通法”，引导学生理解除法的本质，为整数除法的贯通和小数除法的学习打好基础。

三、效果：实现算理算法统整

实施单元教学重构后，利用后测试卷，从算理和算法两个方面检验学生的掌握情况。

从后测数据可知，在仅进行了6课时的学习，且未进行大量练习和技巧训练的情况下，实验班与对照班在除数是两位数的除法的算法掌握上并未出现显著差异。在一些特殊的“障碍点”上，如商的书写位置、笔算除法的竖式以及商中间或末尾有0的情况，也未出现显著差异。然而，对于商末尾有0的除法的习题，实验班在尚未进行例题讲解的情况下，其正确率依然略高于对照班。这充分说明，用算理统领算法是可行的。另外，对于算法在除数是三位数的除法和小数除法上的迁移，实验班的表现也明显优于对照班。可见，算理的理解对算法迁移有积极的促进作用。

通过单元教学重构，学生不仅在算法掌握程度上有所提升，对算理的理解和運用水平也有显著提高。对后测数据进一步分析可知，实验班学生对除法竖式是记录“计数单位细分”过程的理解较为深刻。超过65%的学生能够用横式表示竖式中每一步计算的道理（如图2），并能表示出每一步细分的“计数单位”。在小数除法中，约43.48%的学生能够运用计数单位的细分来解释小数除法的运算过程（如图3）。这表明掌握除法的本质，有助于贯通整数除法和小数除法。

综上所述，重构后的学习路径在教学的过程中不断地进行改善和优化，引导学生厘清整数除法的脉络，形成完整的、具有逻辑性的除法知识结构。学生通过学习，不仅理解了“计数单位细分”的含义，体会到整数除法算理的一致性，还掌握了除法运算的方法，感受到整数除法算理算法的一致性。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022．

［2］巩子坤，张希，金晶，等.程序性知识课程设计的新视角：算理贯通，算法统整［J］.课程·教材·教法，2021，41（6）：89-95.

［3］闫红，张仰勇.大观念下指向学生核心素养的单元整体设计：“除数是两位数笔算除法”单元整合的思考［J］.黑龙江教育（教育与教学），2020（2）：55-57.

（浙江省杭州市富阳银湖实验小学）

*本文系浙江省哲学社会科学规划课题“基于认知发展模型的义务教育教科书编写质量提升研究（编号：23NDJC265YB）”、浙江省高校重大人文社科攻关计划项目“建设高质量教育体系背景下义务教育教科书编写质量提升路径研究（编号：2023GH005）”的研究成果。巩子坤为本文的通讯作者。