两版教材中“分数的意义”内容的比较研究

俞人靖 章勤琼

摘  要：从概念维度和模型维度，结合年级分布和环节分布，对中国北师大版小学数学教材和新加坡小学数学教材My Pals Are Here中的“分数的意义”内容进行分析比较，发现：两版教材中“分数的意义”内容的编排和呈现基本符合学生的认知发展水平，新加坡版教材运用大量的度量模型突出分数的“度量”意义，北师大版教材运用大量的面积模型突出分数的“整体中的部分”意义。由此提出教学建议：明确分数的多种意义，重视“度量”意义；丰富分数的表征模型，增加度量模型；突出单元的核心目标，引领课时学习。

关键词：小学数学；教材比较；分数的意义；概念维度；模型维度

*

本文系国家社科基金2020年度一般项目“大数据支持下的中小学合作型课堂组织形式建构研究”（编号：20BGL127）、福建省教育科学“十四五”规划2022年度基础教育高质量发展重点专项课题“高质量发展视域下课堂教学的评价指标体系构建研究”（编号：FJGHZD22-06）的阶段性研究成果。章勤琼为本文通讯作者。

不论对学生还是对教师来说，分数都是一个充满疑惑和困难的数学模块［1］，所以，在小学数学课程中，分数内容受到大量关注。解决分数问题时，依靠概念性知识的学生会比依靠程序性知识的学生表现得更好［2］，所以，理解分数的概念（意义）位于首要且关键的位置。然而在现实中，学生进行分数运算的能力远强于理解其意义的能力，如学生会运用分数运算规则计算34×12，但不能说明是什么意思。［3］本研究对我国北师大版小学数学教材和新加坡大部分政府学校使用的小学数学教材My Pals Are Here（Marshall Cavendish出版社出版）中的“分数的意义”内容进行分析比较，以期对教学实施（包括教材完善）提出合理建议。

一、 研究框架与方法

小学阶段的分数内容包括分数的认识、分数意义的理解、分数的基本性质、分数的四则运算以及有关分数的问题解决。本研究分析比较的是两版教材中体现分数意义的分数的认识、分数的理解、分数的基本性质内容，不包括体现分数意义的应用的分数的四则运算和有关分数的问题解决内容。

数学内容在教材中有两个维度值得关注：首先是概念维度，即数学内容中的不同概念；其次是模型维度，即表征数学概念的不同模型。本研究从概念维度和模型维度，结合年级分布（北师大版的12册教材中，共有3册涉及分数的意义，分别是三年级上册、五年级上册和六年级上册；新加坡版的12册教材中，共有5册涉及分数的意义，分别是二年级下册、三年级下册、四年级下册、五年级上册和六年级上册）和环节分布（将两版教材的编排划分为四个环节：主题部分、学习部分、活动部分和练习部分。北师大版教材中，目录页上每个单元的标题及标题旁的插图为主题部分；每个课时中要求学生操作、探究的活动为活动部分，其余为学习部分；每个课时后的“练一练”和单元“练习”为练习部分。新加坡版教材中，单元标题页为主题部分，每个课时中的Before you learn和Hands-on Activity中的Work in groups为活动部分，Hands-on Activity中的Try和Chapter Review为练习部分，其余的Learn为学习部分），对“分数的意义”内容进行分析比较。

就概念维度而言，不同学者对分数的概念有不同的理解。Kieren指出分数具有部分整体概念、度量概念、乘法运算子概念、商的概念以及比的概念，并认为部分整体概念是学生学习分数的基础，同时应整体、全面地从各种概念难度去理解分数。［4］Hansen将分数的意义分为整体中的部分、集合中的部分、数线上的数（两个整数间的数）、商和比，并认为教学应根据其对学生认知挑战的程度，从低到高进行。［5］Forrester在Kieren的基础上增加了等值分数，并说明了分数作为算子能使一个量变大或减小。［6］总体而言，对分数的意义进行整理，主要有整体中的部分意义、度量意义、商意义、比意义以及算子意义。［7］将国内外学者对分数意义的理解进行整合，可以对分数的意义做如表1所示的分类和描述。

需要说明的是，对分数的意义进行划分是为了从学科本质上审视教材编排和教学活动，最终目的是让学生对分数意义的理解更为全面和深入，避免因为思维定式造成认知障碍，因此，不能孤立地去理解分数的各种意义。［8］事实上，意义之间也存在著些许重叠，如在“度量”意义中，分数单位是将1平均分得到的，其中的一份就是一个分数单位，这就涉及“整体中的部分”意义。划分后的每个意义强调其侧重的那一方面，如教材中用类似“五个三分之一”这样的语言描述分数，体现出分数是分数单位的累加这一“度量”意义。另外，“乘法运算子”这一意义在分数的乘除计算中体现，更偏向于程序性知识，因此在教材比较中，不对这一意义进行编码。编码时，以每个问题为单位，考虑该问题侧重传达分数的何种意义，进行相应的编码；若一个题目中包含多个小题，且体现不同的意义，则分别计数。

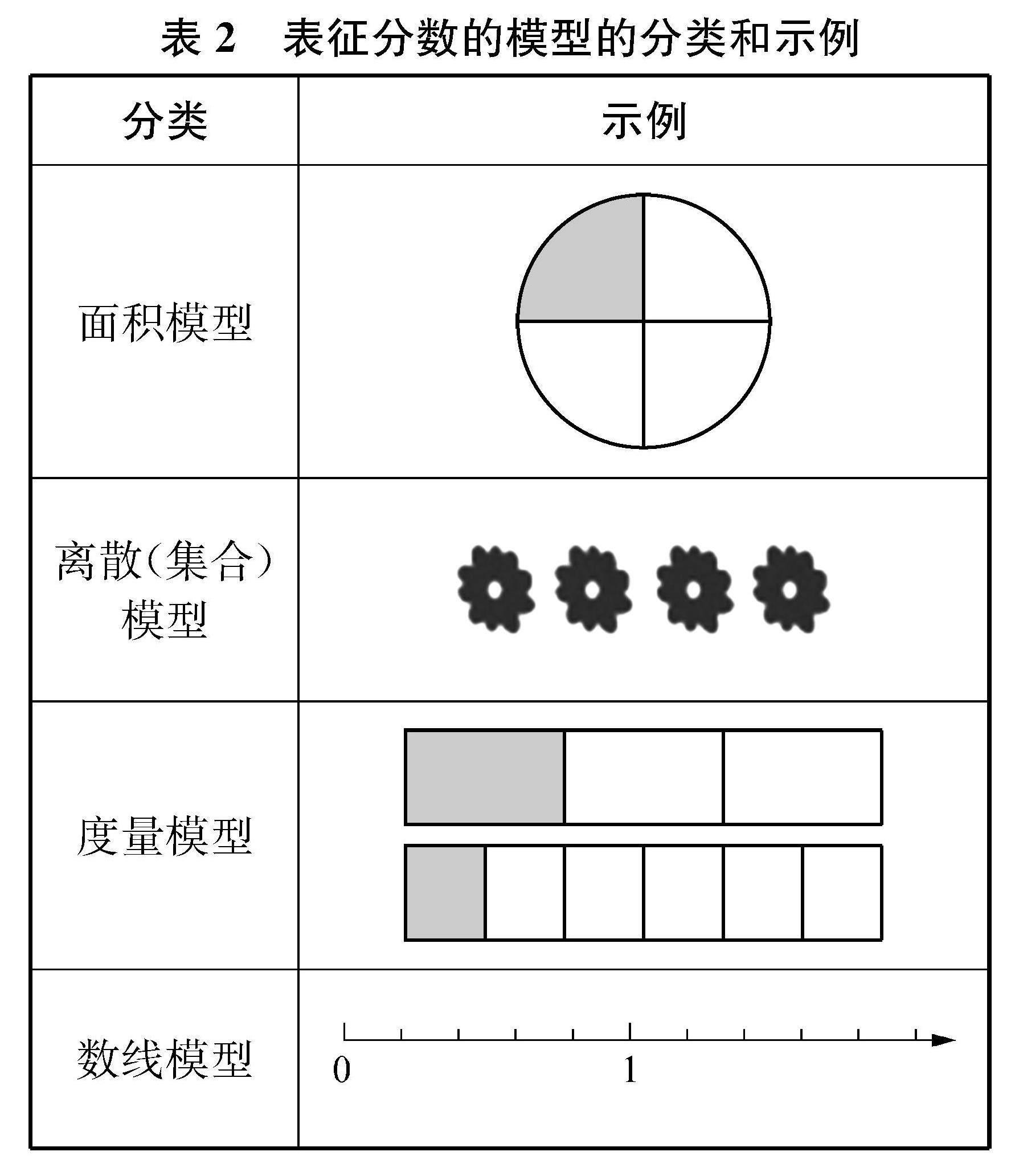
就模型维度而言，Mohan和Tricia指出在分数教学中常用到的几个模型，包括面积模型、离散模型和度量模型。［9］此外，Sitti等人在研究中发现，数线对学生学习分数有很大的支持作用。据此，将表征分数的模型分为四类，如表2所示。

面积模型强调一个整体被平均分成多份后，涂色部分的大小或其与整体的关系。离散（集合）模型是指以多个事物组成的集体为一个整体，用分数表示其中一个或多个与整体的关系。度量模型侧重分数单位的识别和累加，即先确定分数单位，再通过分数单位的累加形成分数。数线模型可以看成度量模型的进一步抽象，同样强调分数单位的识别，在此基础上确定分数在数线上的位置，并将整数与分数相联系。结合表征分数的模型和分数的意义来看，面积模型和离散（集合）模型更侧重“整体中的部分”意义，度量模型和数线模型更侧重“度量”意义。编码时，若同一个问题中呈现不同的模型，则分别计数；若同一个问题下多次出现某个类别的模型，则多次计数。

二、 研究结果与分析

（一） 概念维度

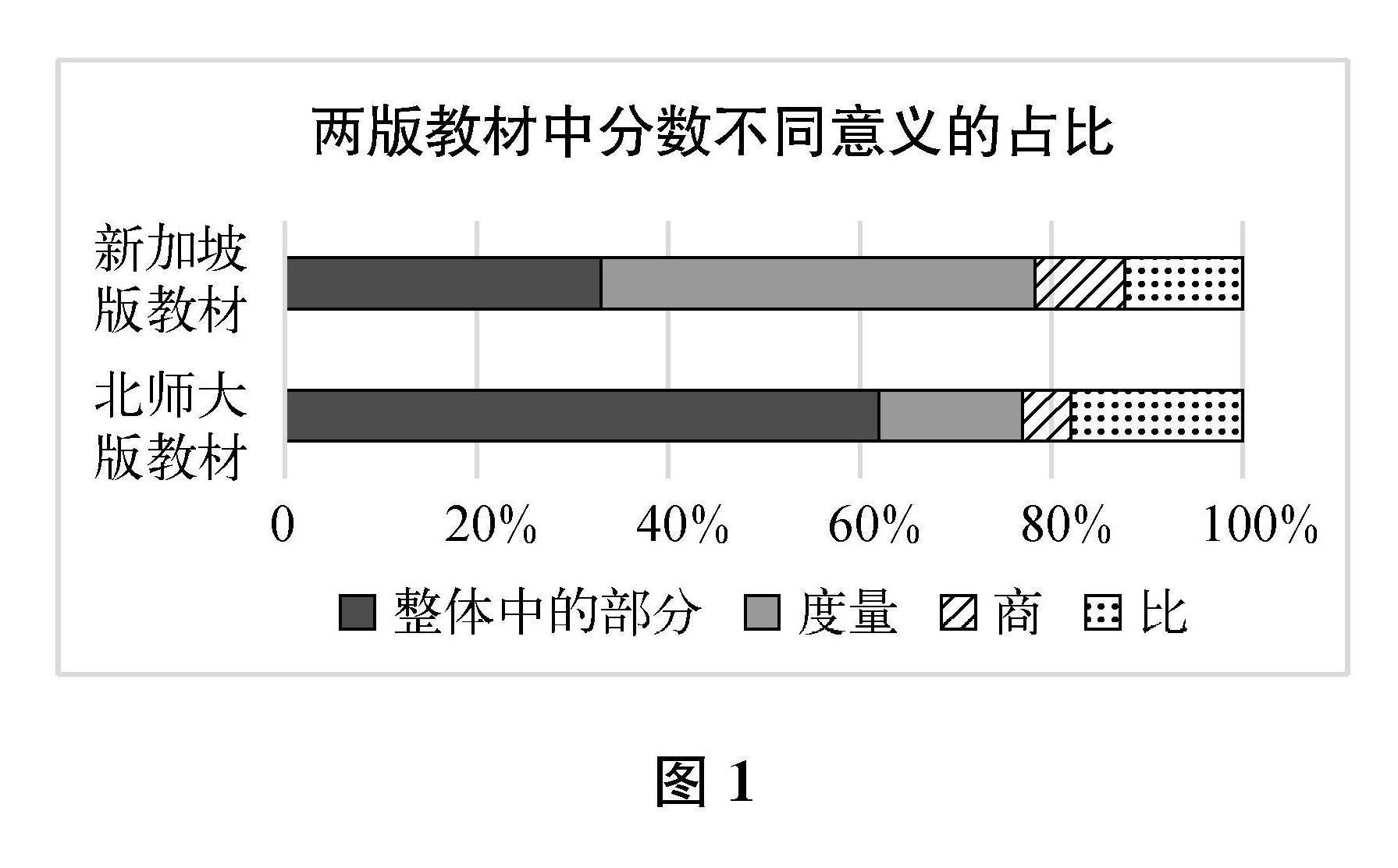
两版教材中分数不同意义的占比如图1所示。可见，新加坡版教材中，“整体中的部分”意义和“度量”意义占比较大（分别为33.0％和45.3％），“商”意义占比最小（仅为9.4％）；北师大版教材则将重点放在“整体中的部分”意义上（占62.0％），相对忽视了“度量”意义（仅占15.0％）。

两版教材中分数不同意义的年级分布如下页表3所示。

可见，新加坡版教材中，“整体中的部分”意义集中于二、三年级，四至六年级虽然也有涉及，但是明顯减少。另外，在二年级刚接触分数时，新加坡版教材就开始向学生渗透“度量”意义，且从二年级到四年级越来越多，直至四年级重点学习。五年级开始介绍“商”意义，但是“商”意义占比最小，六年级便不再继续渗透和应用。“比”意义集中于六年级：此前的学习中，学生处理的对象仅限于一个；而六年级时，学生需要用分数表示两个量之间的关系，并用分数表示比值，同时需要识别分子和分母分别代表哪个量。由此推测，在新加坡版教材编写者看来，学生对“整体中的部分”意义和“度量”意义的理解是并驾齐驱的，“商”意义对学生的认知能力（特别是抽象能力和联系能力）要求较高，“比”意义挑战性最强。

北师大版教材在三年级初次引入分数时，大篇幅集中呈现“整体中的部分”意义。到五年级，介绍“度量”意义；同时，“整体中的部分”意义还在延续，且数量接近“度量”意义的两倍。“商”意义安排在五年级，但所占篇幅同样很小，且只用一个字母式表示分数与除法的关系。另外，在五年级虽然没有明确介绍“比”意义，但是能在一些练习中发现“比”意义，即用分数表示两个量之间的关系，如“山娃家一共养了6只羊，8只鸭子，20只兔子，羊的只数是鸭子的几分之几？羊的只数是兔子的几分之几？”。真正介绍“比”意义是在六年级，但更多的是用分数表示比值，用分数化简比值。可见，北师大版教材着重于“整体中的部分”意义，在“比”意义方面更关注分数表示、化简比的程序性作用。

两版教材中分数不同意义的环节分布如表4所示。从中也能看出两版教材对分数不同意义的重视程度。新加坡版教材明显体现出主题部分的引导作用，每一单元的主题页中都有说明性的单元大观念及课时安排，重点突出，阶段明确；同时，单元内每一个环节集中体现的意义与主题页呈现的意义相符。此外，学习部分和活动部分是新加坡版教材体现分数意义的主要环节，而学习部分和练习部分是北师大版教材体现分数意义的主要环节。

（二） 模型维度

两版教材中表征分数不同模型的占比如图2所示。新加坡版教材中，面积模型与度量模型占比相近，都接近50％，离散模型和数线模型占比很小。可见，它更偏向于运用连续量的平均分模型帮助学生理解部分与整体之间的关系——只于四年级用分数表示一个集体中的一部分时采用离散模型；更多采用度量模型帮助学生理解分数单位的累加——虽在三、四年级将度量模型进一步抽象成数线模型，要求学生将分数对应到数线上的点，但是数线模型出现的频次相比于度量模型少得多。北师大版教材中，面积模型占比最大（为63.3％），离散模型其次，而度量模型和数线模型占比非常小。其中，度量模型和数线模型占比基本持平，而离散模型、度量模型、数线模型的总占比远低于面积模型的占比。

图2

两版教材中表征分数不同模型的年级分布如表5所示。可见，新加坡版教材中，面积模型在二、三年级占比最高，度量模型在三、四年级占比最高；三年级是转折点，度量模型

的应用远高于面积模型；度量模型贯穿学生学习分数的整个阶段。北师大版教材在三年级呈现面积模型和离散模型，并以面积模型为主；五年级时面积模型的数量减少，离散模型的数量基本不变，且面积模型和离散模型的总和接近度量模型和数线模型总和的三倍。

两版教材中表征分数不同模型的环节分布如下页表6所示。横向看，新加坡版教材重视面积模型和度量模型，在主题部分和活动部分更多地采用面积模型，在学习部分和练习部分更多地采用度量模型，而离散模型和数线模型较少；北师大版教材不论在学习部分、活动部分还是练习部分，都使用大量的面积模型。纵向看，新加坡版教材在学习部分和活动部分使用的模型数量都大于或接近练习部分；而北师大版教材中的模型更多地体现于练习部分，即通过题目呈现模型。

三、 研究结论

综合上述两个维度的研究结果，可以得到两版教材比较研究的结论：

（一） 共同点：两版教材中“分数的意义”内容的编排和呈现基本符合学生的认知发展水平

两版教材初次引入分数时，都采用“整体中的部分”这一意义，引导学生从部分与整体关系的角度认识分数。体现“整体中的部分”意义的“平均分”情境在生活中非常常见，对学生来说挑战较小。以此引入，符合学生自主建构知识的规律，同时能够调动学生的已有经验，支撑学生直观地理解分数。

此外，在学生初次接触分数的二、三年级，两版教材都利用大量的表征模型，结合大量的生活情境，帮助学生顺利地认识这一相对整数来说较为“奇怪”的数的意义，比如让学生将代表一块比萨的圆平均分成4份，得到1份就是14块比萨，也是整块比萨的14。学生在操作图形的过程中与分数的意义相联系，顺应具体形象的认知发展水平。而在五年级学习“商”意义、六年级学习“比”意义时，两版教材中表征模型的呈现次数都显著减少，特别是在学习“商”意义时。其原因可能与五、六年级学生的认知发展水平向形式运算阶段过渡，抽象概括、想象能力进一步发展有关，也可能与将整数除法算式写成分数形式这一较为程序性的操作有关。

（二） 不同点：新加坡版教材运用大量度量模型突出分数的“度量”意义，北师大版教材运用大量面积模型突出分数的“整体中的部分”意义

新加坡版教材十分重视“度量”意义，从“整体中的部分”意义引入分数后，在学习分数的第二阶段就将“度量”意义放在主要位置。编排上，一方面，体现分数学习的连续性，即从二年级开始，每个年级都有分数的学习，且不同年级有不同的侧重点；另一方面，体现“度量”意义教学的一贯性，即二年级以“整体中的部分”意义为主，同时伴有“度量”意义的认识，此后每个年级都将“度量”意义的理解和运用渗透到学习内容中。另外，新加坡版教材使用了大量的表征模型（总数接近北师大版教材的两倍），即格外重视几何直观对学生思维的支持作用。同时，教材中的活动部分和学习部分通常与表征模型相结合，帮助学生在活动中建构学习经验，理解分数的意义。在四种表征模型中，使用最多的是度量模型，它不仅贯穿学生学习分数的整个阶段，还在三、四年级占主体地位。

北师大版教材偏好通过“整体中的部分”意义帮助学生在不同阶段理解分数，在学习分数的三个阶段，几乎都将“整体中的部分”意义置于关键位置。这一做法在初学分数时，能够让学生快速地建立“平均分”情境，更容易接受和理解分数；但在后期学习假分数及分数与除法的关系时，则容易造成学生的认知障碍。此外，北师大版教材更多地使用面积模型和离散模型，因此，学生会对“整体中的部分”意义掌握得较好。同时必须注意到，教材运用的表征模型数量较少，常常使用单一的文字语言描述问题及其情境，且学生的实际操作活动较少，这就要求学生具备较高的抽象能力，才能理解分数的意义、解决问题。特别是六年级学习分数“比”意义时，几乎不采用表征模型引导学生直观地体会两个量的关系，这会使原本就抽象的分数放到問题情境中时更加抽象和难以理解。

值得一提的是，新加坡版教材很好地体现了目标导向作用，每个单元起始都有能够体现本单元核心内容和目标的主题页，其中的大观念即本单元的核心目标。如二年级分数单元主题页中的大观念为“分数可以用来描述平均分的部分是如何与整体相联系的”，这表明本单元中分数的“整体中的部分”意义是重点。相比之下，北师大版教材缺乏能够引领整个单元的大观念，如五年级同时呈现了“整体中的部分”“度量”“商”“比”四种意义，但可惜的是，无论是“度量”“商”还是“比”意义，都没能在新一个阶段取得主角的地位。

四、 教学建议

基于上述研究结论，可以得到关于“分数的意义”内容的教学建议（从某种角度看，也是对我国教材修订的建议）：

（一） 明确分数的多种意义，重视“度量”意义

分数的意义内涵丰富，将其分类并明确表述，学生才能对分数有更为全面的理解，以避免只关注“整体中的部分”意义这一隅，导致无法延续后面假分数、分数四则运算的学习。同时，需要考虑分数的各种意义及其联系在年级上的合理分布，尽可能在每一学年都让学生见到“熟悉”的分数，通过更有连续性的学习帮助学生螺旋式上升地理解较为抽象的分数。

可以认为，“度量”意义是最能够体现分数作为数的本质的意义，在学生学习分数时起贯通作用。例如，假分数的认识就可以由“度量”自然地过渡，用14作为单位量，量3次有3个14，就是34，量5次有5个14，就是54。因此，教师需要认识到“度量”意义在学生后续分数学习中的解释作用，在教学中提升“度量”意义在所有意义中的比重，并且让“度量”意义贯穿学生分数学习的整个阶段。

教学时，为了厘清分数的多种意义，需要把握每种意义的学习目标和核心。比如，“整体中的部分”意义的学习目标是理解平均分的部分与整体的关系，其核心是将分数的表示与平均分后取份数的过程相对应；“度量”意义的学习目标是理解分数与整数、小数在数本质上的一致性，其核心是分数单位累加得到分数；“商”意义是分数的真正来源［10］，即分数源于两个整数相除不能得到整数时数系扩充的需要，其核心是理解整数除法可以写成分数的原因，不能只是简单地将整数除法中的被除数和除数与分数的分子和分母相对应。此外，当“整体中的部分”意义过渡到“度量”意义后，就应常用“度量”意义来建构学生对分数的深刻理解。如学习“商”意义，即为什么a除以b可以写成ab，可以做如下解释：a除以b也就是将a中每个1除以b，则1b就是一个单位，一共有a个，就是ab。

（二） 丰富分数的表征模型，增加度量模型

在现实中，不少学生无法利用图示表征分数问题，特别是六年级分数表示两个量之比时；此外，有学生能运用运算法则或解题技巧快速进行分数计算和问题解决，却无法说明为什么要这样算，为什么能这样算。小学高年级学生的思维虽然逐渐向抽象水平发展，但是仍然以具体形象思维为主导，因此，面对抽象的分数问题，仍然需要直观模型来辅助。对此，教师首先需要呈现大量的直观模型，引导学生运用丰富的表征模型理解分数的多种意义。

通常，教学“分数的初步认识”，即“整体中的部分”意义时，教师会选择大量的面积模型来帮助学生理解分数。这种方式到了学习假分数等内容时，便有可能成为学生理解的阻碍。对此，后续教学“分数的意义”时，教师应该更多地选取度量模型，通过分数单位向学生呈现分数，从而帮助学生跳脱出“平均分”情境，从数的一致性上理解分数。在此基础上，还要逐步地过渡到更为抽象的数线模型，从而帮助学生真正理解分数与整数、小数的一致性，对数系有更完整的理解。

当然，学生对分数的不同表征反应了其对分数意义理解的水平层次。因此，在重视度量模型和数线模型的同时，也要关注表征的丰富性，从分数意义的不同方面理解分数，解决问题。例如，教学分数的基本性质时，既可用面积模型，从部分与整体关系的视角解释，也可用度量模型，从分数单位的视角解释。

（三） 突出单元的核心目标，引领课时学习

《义务教育数学课程标准（2022年版）》提出了“整体把握教学内容”“重视单元整体教学设计”的建议。为此，明确单元核心目标尤为关键。明晰了分数的多种意义后，教师可以对各种意义做整体思考和规划，在每个单元的教学中突出核心目标，从而引领课时教学的方向。具体地，首先要以整体化的视角审视单元知识之间以及当前阶段知识与下一阶段知识之间的联系，在此基础上将核心目标分解成具体的可评价的表现性目标，即达成这一目标时学生需要有什么样的表现，然后便可以设计出与目标相对应的学习任务，引发学生的学习活动。

学生的学习活动经验，包括探究经验、互动经验、游戏经验等，都是其自主建构知识的丰富土壤。在单元核心目标的引领下，可以设计丰富多样的学习活动，让学生在实践、探究、体验、合作、交流中感悟分数的基本思想，积累关于分数的基本活动经验，从而促进学生全面、深刻地理解分数。比如，在“度量”意义的教学中，设计度量活动让学生重走古人之路：以1张纸条为单位来测量物体的长度，当不能刚好用“几张纸条”来表示物体的长度，且纸条太长时，将纸条对折，产生几分之一的分数做测量单位，得到测量结果。再如，设计将分数大小比较与扑克牌游戏相结合的活动、找朋友合成“1”的活动等。

参考文献：

［1］ M.Chinnappan，T.Forrester.Generating procedural and conceptual knowledge of fractions by pre-service teachers［J］.Mathematics Education Research Journal， 2004（3）：872.

［2］ D.Hallett，T.Nunes，P.Bryant.Individual differences in conceptual and procedural knowledge when learning fractions［J］.Journal of Educational Psychology，2010（2）：395406.

［3］ M. Aksu. Student Peformance in Dedling with Factions［J］.The Journal of Educational Research，1997（6）：375.

［4］［5］［8］ J.Mills.Developing Conceptual Understanding of Fractions with Year Five and Six Students［D］.Hamilton：The University of Waikato，2013：480，480，480.

［6］［9］ T.Forrester.Generating procedural and conceptual knowledge of fractions by pre-service teachers［J］.Mathematics Education Research Journal，2014（3）：883，883.

［7］ 章勤琼，徐文彬.论小学数学中分数的多层级理解及其教学［J］.课程·教材·教法，2016（3）：4349.

［10］ 张奠宙.分数的定义［J］.小学教学（数学版），2010（1）：4849.

（俞人靖，浙江省嘉兴市实验小学。章勤琼，福建师范大学教育学院，教授，博士生导师。）