控制变量法在二次函数教学中的应用解析

侯立峰

【摘要】在科学实验中，经常会采用控制变量法来探究某一因素对实验结果产生的影响.在数学研究中适当地引入控制变量法可以帮助解决一些研究的困顿点，便于观测，促进理解，让思维更具条理性.本文就将结合具体的教学案例，解析控制变量法在二次函数教学中的具体应用.

【关键词】控制变量法；二次函数；应用解析

1 引言

细读人教版教材我们知道在二次函数这一章节，教材先是从实际生活情境中引出各种形式的二次函数（有不含一次项的、不含常数项的等），接着对特殊的情形进行一般化的处理，归纳出二次函数的一般式y=ax2+bx+c（a≠0）.但是在探究二次函数图象和性质时教材却没有从一般式入手，而是从顶点式进行研究，这样的研究方法其实是受限于二次函数图象的复杂形式，如果直接从一般式入手，学生可能无法正确画图，更不用谈借助函数图象研究函数的性质.但是这样的研究脉络显然和一次函数有所不同，一次函数在研究时是直接根据解析式多点画图，然后在观测完图象特征后，才采取与正比例函数进行融合，从而引出用平移研究函数图象的方法，但在二次函数这里，却是一开始就用平移法研究一般化的图象，而不是用多点作图，这会对学生的认知经验产生冲突，所以“用顶点式研究函数”的合理性和必要性需要教师在起始课就要阐明，引入控制变量法可以很好地解决这个问题，同时控制变量法也是二次函数应用中的常见分析方法.

2 变中不变，数形结合

基于核心素养的要求，我们应该在教学中教会学生研究数学问题的一般套路，以及帮助学生建立对研究方法科学性的认识.所以“用顶点式研究二次函数”的合理性和必要性是二次函数教学的难点和关键点.我们不妨先让本章延续一次函数的研究思路，用描点法画出函数图象，但是因为二次函数的形式过于多样，学生画图存在困难，哪怕顺利画出图象，也难以对所画出的图象进行分类和归纳，总结出共性（函数性质）.在一次函数y=kx+b（k≠0）中，“系数变量”只有两个，基于正比例y=kx（k≠0）的学习经验，学生基本能联想到k的正负影响图象的增减，至于b影响图象与y轴的交点位置，也是比较直观的一种数形转化，学生可能会没有注意到x的次数对图象形状的影响.到了二次函数，“系数变量”变成了3个，x的次数也发生改变，为确保学生拥有研究函数的一般经验，按照一次函数的研究逻辑，我们需要运用控制变量法完成以下关键教学环节：

环节一 类比学习

师 面对新类型的函数，我们将如何进行研究？

生 类比于之前学过的一次函数.

师 你们还记得一次函数研究的模式吗？请类比说出二次函数接下来可能的研究思路.

生1 从最简单的二次函数y=x2入手.

生2 研究它的图象和性质.

生3 研究a、b、c对函数图象的影响.

生4 用它的图象和性质解决一些综合应用问题（比如方程、不等式、几何图形、应用题等）.

环节二 用y=x2做好观测与记录

师 我们之前在学习画函数图象时画过y=x2（x>0）的图象，大家还有印象吗？我们一起回忆一下（用信息技术直接呈现作图过程，帮助学生回忆）.

师 大家能快速画出y=x2的图象吗？（请学生到多媒体前，在y=x2（x>0）的表格和图象基础上进行绘图补全，方便学生发现它轴对称的特征）.

师 你能描述下这个图象的特点吗？（引导学生类比一次函数进行多角度描述）.

生1 形状是曲线.

生2 图象从左往右，先下降再上升（增减性的图象语言）.

生3 经过一、二象限（所处象限）.

生4 原点很特殊，是图象的最低点（关注顶点，有别于一次函数的新特征形式）.

生5 看起来像是轴对称图形（有别于一次函数的新特征形式）.

生6 在y轴左边，y随x的增大而减小；在y轴右边，y随x的增大而增大（增减性的文字语言）.

师 改变a的值，我们再来畫图，画图过程中请大家观测上述特征是否有发生变化？

在这一过程中，教师归纳出二次函数的形状（抛物线）、三个要素（开口、顶点、对称轴）和一个性质（轴对称性质）.

师 这里只是画了很多y=ax2（a≠0）的图象，那么所有的二次函数y=ax2+bx+c（a≠0）都有这些特征形式吗？

生 应该是，一次函数也是这样，和正比函数图象形态上一样，正比例是它的特殊情况.那么，可以猜测同一种类型的函数，图象形态上可能会一样.

师 非常棒的猜想，那你们能猜猜看，为什么二次函数图象会是曲线，而不是折线，或者跟一次函数一样是直线？

生 可能是自变量的次数为2造成的.

师 特别好，不过刚才大家所猜测的，还需要画更多的图来印证.

师 抓住二次函数的形态、要素、轴对称性就可以很好地绘制二次函数的图象.

环节三 用控制变量法来探究a、b、c对函数图象的影响

师 在观测y=ax2（a≠0）的图象时，我们发现它们开口的方向与大小受a的影响，而它们的对称轴都是y轴，顶点都是（0，0），不会因为a的数值改变而改变.结合一次函数解析式常数k、b对图象特征的影响，于是我们就得到猜想：（1）因为没有b、c，所以二次函数的开口方向和大小只跟a的数值有关；（2）因为y=ax2（a≠0）的对称轴都是y轴，顶点都是（0，0），所以二次函数的对称轴和顶点和a的数值无关，可能跟b、c的数值有关.这样的猜想对吗？

生 不对，这是b=0，c=0的特殊情形，并不能代表其他情形也是这样.

师 那我们要怎样做才能得出正确的论断.

生 我们可以再选几组b，c取其他值的情形，然后再确定b，c的基础上，改变a的数值，来论断第一个猜想是否正确.

师 特别好的方法，像这样保持其他因素不变，而观测一个因素对结果产生影响的方法叫做控制变量法，我们一起来试试看.

（举例：y=ax2+x+2，y=ax2－2x+3，分别改變两个函数a的数值.）

师 这样就能说明二次函数的开口方向和大小只跟a的数值有关吗？

生 不行，还需要不改变a的数值，改变b，c的数值再来看下.

生 需要b，c分开来讨论.

（操作一：控制a、b的值不变，改变c的数值，做多次演示；操作二：控制a、c的值不变，改变b的数值，做多次演示.用信息技术演示和结果对照，帮助学生理解二次函数的开口方向和大小跟b，c的数值无关.）

师 于是我们就可以确定第一个猜想是对的.第二个猜想，大家可以用同样的方法来验证吗？

生 其实在刚才的实验过程中，我发现保持b，c的数值不变，改变a的数值过程中，二次函数的对称轴和顶点的位置也发生改变，所以这两个要素跟a的数值也有关.

师 非常细心地观察，其实在使用控制变量法时，经常会得到不止一个结论.你们还有其他发现吗？

生1 控制a、b的值不变，改变c的数值演示过程中，我发现二次函数的对称轴位置不变，但顶点的位置发生了改变，并且这些二次函数与y轴交于同一个点.

生2 控制a、c的值不变，改变b的数值演示过程中，我发现二次函数的对称轴和顶点位置都发生了改变.

师 两位同学的发现我们可以通过多组控制变量法实验操作来进行验证.总结一下，我们可以得到这样的结论：二次函数的开口方向和大小只跟a的数值有关；二次函数的对称轴位置跟a、b的值有关；二次函数的顶点位置跟a、b、c都有关；二次函数与y轴的交点，只与c的值有关.

环节四 论述平移法的合理性

师 因为二次函数的图象特征受多系数变量的影响，所以用多点作图法画二次函数的图象难度较大，那我们还可以用什么方法来研究二次函数的图象？

生 用平移的方法.

师 你是怎么想到的？

生 一次函数的图象就可以看作由正比例函数y=kx平移得到，二次函数的图象也可以看作由y=ax2平移得到.

（注：在得到二次函数的顶点式y=a（x－h）2+k后，还需要把它跟一般式进行式子结构的对比，阐明形式上的一致性，从而再次证实用平移法研究二次函数图象的合理性.）

上述的教学环节，通过控制变量的实验方法，帮助学生从变中探索不变，从图象形态的变化观测系数变量的数值对函数性质的影响，从而让学生明白研究函数的方向是一致的，但是在研究的方式上有的时候需要做适当的调整.

3 简化思路，寻求突破

为了保证函数学习脉络的一致性，我们可以选择运用控制变量法对二次函数的图象研究进行关键性的铺垫.同样，我们还可以把控制变量法运用到解决二次函数的一些实际应用题中，强化学生对二次函数模型的认识.比如，在围栏问题中，围栏的形状、围栏的格数、墙的长度等变量都会对围栏的面积最值有影响，当这些变量在同一道题中出现，学生不容易找到解题的突破口.那么，我们就可以用控制变量法分解出几个小问题进行逐一的分析.

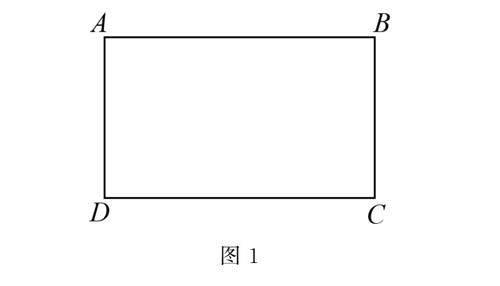
问题1 如图1用一段长为30m的篱笆围成一个矩形养鸡场，这个矩形的长、宽各为多少时，养鸡场的面积最大？最大面积为多少？

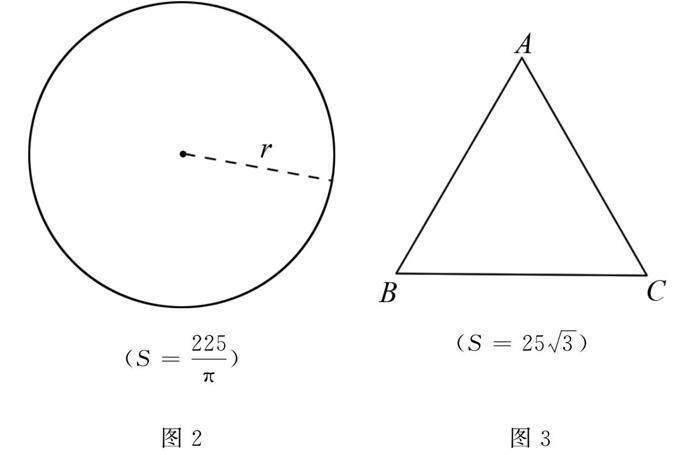
先从最简单的情形入手，探讨在矩形形状下控制篱笆的总长不变，改变长、宽，如何达到围栏的面积最大.这时候围栏的面积同时受长和宽两个变量的影响，因为周长一定，所以导致长宽之间满足一定的数量关系，从而围栏的面积就可以只受单一变量的影响.接着在不改变所用篱笆长度的情况下，把围栏的形状改为圆（如图2）或者等边三角形（如图3），从而讨论图形的形状这一变量对围栏面积的影响，显然，当周长一定时，圆和等边三角形的面积问题中不存在变量，可以通过列简单的算式进行求解.

接下来如果要探讨围栏格数对围栏面积的影响，就可以选用矩形形状的情形进行重点分析（圆和等边三角形可以留给学生自行探索）.

通过运用控制变量法，把综合的围栏问题分解成若干个小问题，帮助学生逐一地进行分析，培养学生更清晰的推理意识和模型观念.这样分析问题的方式，可以运用到解决多变量的综合问题中.

随着数学知识的复杂化、生活化，多因素多变量的情境越来越常见，在教学中引入控制变量法，是数学学科的基本要求.控制变量法可以让问题研究更有着力点，降低问题的抽象程度，让解决问题的主线更加的明确.所以，不仅要在课堂教学中传授给学生控制变量法的基本实施经验，还要关注学生的具体应用成效.

参考文献：

［1］王晓敏.立足课堂 提升能力——以“二次函数的图象与性质”教学为例［J］.中学数学.2023（12）：20-21.

［2］严美芹.二次函数与实际问题常见题型梳理分析［J］.中学数学.2023（08）：95-96.