初中几何问题解题中的证明策略与方法研究

魏倩倩

【摘要】本文主要探讨初中几何问题解题中的证明策略与方法，具体涉及基本解题步骤和具体解题策略等方面的内容.文中简要阐述初中几何证明题的基本解题步骤，包括理解题目、分析已知条件、确定证明方向等.在此基础上，提出善于挖掘及利用题目图形中的隐藏条件、运用直接证明法进行几何证明和利用反证法进行几何证明三种具体解题策略.通过本文的研究，可以对初中几何证明题的解题思路和方法进行总结和归纳，从而为学生解决几何问题提供一定的参考.

【关键词】初中数学；隐藏条件；解题策略

1 初中几何证明题基本解题步骤

第一，理解题目是解题的第一步.仔细阅读题目，了解所给条件和需要证明的结论.

第二，分析已知条件是解题的关键.将所给条件进行分类整理，确定已知条件之间的关系，并利用几何知识进行推导和联想.

第三，确定证明方向.根据题目中所给的结论，判断证明的方法，常见的证明方法包括直接证明法、反证法、数学归纳法等.

第四，构建证明过程.根据已知条件和证明方向，运用几何知识和推理方法，逐步推导需要证明的结论.在推导过程中，应注重逻辑严密，避免漏洞和错误.

2 初中几何证明题的具体解题策略探讨

2.1 善于挖掘及利用题目图形中的隐藏条件

在解决初中几何证明题时，善于挖掘和利用题目图形中的隐藏条件是一种有效的解题策略.通过观察和分析图形，可以发现那些在题目中没有直接给出但可以推导出来的条件，从而更快地得出证明结果.

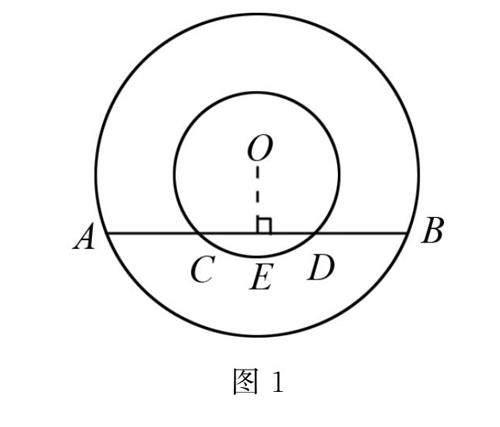
例1 如图1所示，两个圆都以点O为圆心，一条不过直径的直线交外圆于点A、点B，与内圆相較于点C、点D，试证明AC=BD.

解析 首先可以通过观察题目图形寻找隐藏条件，在这个题目中，认真观察发现两个圆的圆心均为点O.根据圆的性质可知，OA=OB.尽管这个条件没有明确给出，但它是一个隐藏条件，可以为后续的证明过程提供线索.

根据已知条件和图形特点，可以使用直角三角形的性质来展开证明.过点O作AB的垂线，并连接OA，OB.在△AOB中，因为两条边OA和OB是外圆的半径，所以△AOB是一个等腰三角形，由等腰三角形的性质可知∠OAB=∠OBA.

接下来，则需要找到与AC和BD有关的条件.观察图形可以发现，当连接点A和点B到点O时，可以得到Rt△AOE和Rt△BOE.这是另一个隐藏条件，可以作为进一步推导的线索.

考虑△OEC和△OED，它们的斜边OC和OD分别为内部小圆的半径，同样根据圆的性质，△OEC和△OED都是等腰三角形.因此，CE=ED.

综上所述，通过挖掘隐含条件，最终可以得到两个关键的等边关系：AE=BE，CE=DE，那么相应地可得到线段AC=BD，由此便完成了该几何证明题的解答.

小结 通过以上分析，可以看到善于挖掘和利用题目图形中的隐藏条件是解决初中几何证明题的重要策略.通过观察和发现隐藏条件可以引导证明的方向，加强证明过程中的推理和推导.

2.2 运用直接证明法进行几何证明

直接证明法是解决初中几何证明题最为常用的方法，是基于逻辑推理和已知条件，通过一系列明确的步骤来证明所要证明的结论.

例2 在△ABC中，AE作为△ABC外角的平分线，且有AE∥BC，试求证AB=AC.

解析 就该几何证明例题而言，可以根据求证问题逐步考虑，循序渐进地求出最终结果.具体而言，在三角形中，证明两条边相等最为常用的方法便是证明对应的两个角相等.如图2所示，只要证明∠B=∠C，则可证明△ABC为等腰三角形，根据等腰三角形的性质便可以得出AB=AC的证明结论.

根据上述思路，首先可以结合已知条件“AE为△ABC外角的平分线”得出∠DAE=∠CAE.再次分析题目已知条件，即AE∥BC；结合平行线定理，可以由此推出∠DAE=∠CAE，∠C=∠CAE.

通过分析题目已知条件最终得出∠DAE=∠CAE，∠DAE=∠ABC两个关系，整合后可知四个角都相等，即∠DAE=∠ABC=∠B=∠C，由此可知在等腰三角形ABC中，有AB=AC.具体的解答过程如下.

证明 因为AE为△ABC外角的平分线，

所以∠DAE=∠CAE.

因为AE∥BC，根据平行线定理可得∠DAE=∠ABC，

同时也可以推出∠C=∠CAE.

结合上述所推导出的等角关系，

可知∠DAE=∠CAE=∠B=∠C，

所以△ABC为等腰三角形，根据等腰三角形的性质可知其两条腰长相等，

即AB=AC.

小结 经分析可知，在几何证明题解答过程中，通常可以先结合题目已知条件进行逐步推导，将所推导出的内容进行整合，由此可以直接解决很多问题.

2.3 利用反证法进行几何证明

利用反证法进行几何证明是一种常见的解题策略，该方法通过假设所要证明的结论不成立，然后推导出矛盾的结果，从而得出所要证明的结论必定成立的结论.

例3 如图3所示圆O中两条非直径弦分别为CD，AB，两弦相较于点M，求证：AB与CD不能互相平分.

解析 此处以逆向思维假设AB与CD能互相平分，平分点为M点，由已知条件可知AB，CD均不是圆O的直径，即相交点M并非圆心.连接OA，OB以及OM.根据既定假设条件，AB与CD相互平分，且平分点为M，那么有AM=BM，所以M应该是线段AB的中点，且根据圆的性质可知，OA和OB是圆的半径，因此OA=OB，所以△AOB为等腰三角形.在等腰三角形中，底边中点与顶点的连线即为三角形的高，所以OM⊥AB.同理，在△OCD中，M平分CD即为CD的中点，因为OC=OD，△OCD为等腰三角形.根据等腰三角形的性质可知，OM⊥CD.经分析可知，假设CD和AB平分于点M，那么过点M的两条直线AB，CD都将垂直于M，而二者间本身相互矛盾，因此可知AB与CD可以相互平分的假设不成立，故AB与CD无法相互平分.

小结 在实际应用中，利用反证法进行几何证明可以帮助我们深入理解图形和已知条件，并且有助于发现问题中隐藏的规律和特点.

3 结语

初中几何问题解题中，证明策略与方法是非常重要的.常用的证明方法包括直接证明法、间接证明法、反证法、数学归纳法等.在选择证明方法时，需要根据已知条件和所求结论的性质进行综合考虑，并灵活应用各种方法，通过多种方法的灵活运用，可以帮助学生有效地解答各类几何证明题.

参考文献：

［1］白方.几何变换思想在初中几何教学中的渗透与应用研究［D］.上海：上海师范大学，2021.

［2］程香红.问题提出教学法在初中几何教学中的应用研究［D］.上海：上海师范大学，2021.

［3］郑高攀.化归思想在初中几何解题中的应用研究［D］.漳州：闽南师范大学，2021.