初中数学解题中辅助圆的应用分析

欧露

【摘要】在初中数学解题中，并不是所有的题目都可以采用常规的解题方式，对于一些比较复杂的问题，需要转变解题思路，引入相应的辅助圆，完成问题的解答.通过辅助圆的构造和应用，能够发掘题目中的隐藏信息，简化题目，使得问题更加简单，帮助学生快速解决问题.本文分析辅助圆在初中数学解题中的应用.

【关键词】初中数学；辅助圆；解题教学

在初中数学解题中，几何题是重要的题目类型，主要研究图形结构以及空间关系，相对于代数题来说，此类题目比较直观，但是对学生的空间观念要求较高，对于一些难度大的题目，仅依靠题目中的图形难以解题，教师可以引导学生巧妙利用辅助圆，通过辅助圆的构造，对题目条件进行处理，从几何图形中发现隐藏信息，有效分析解题思路，快速解决数学问题.

1 利用辅助圆，解决线段长度问题

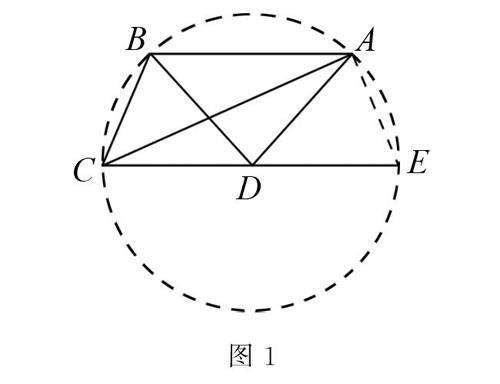
例1 在四边形ABCD中，AB∥CD，AD=DC=DB=2，BC=√7，求解对角线AC的长度.

解 如图1所示，延长CD与半径为2的圆D相交于点E，连接AE，

所以点A，B，C在圆上，

因为AB∥CD，

所以弧BC与弧AE的长度相同，

所以BC=AE=√7，

在△ACE中，∠CAE=90°，

CE=4，AE=√7，

所以AC=3.

2 借助輔助圆，解决求度数问题

例2 如图2所示，在四边形ABCD中，连接AC，AC=BD，∠BAD=∠BCD=90°，∠BDC=25°，求解∠BAC的度数.

解 取BD的中点O，以O为圆心，OA为半径作圆，如图3所示.

因为∠BAD=∠BCD=90°，

所以点A，B，C，D四点共圆，

所以∠BAC=∠BDC，

因为∠BDC=25°，

所以∠BAC=25°.

3 利用辅助圆，解决图形面积问题

例3 已知BC=6，点A为BC上方的动点，∠BAC=120°，点D为BA延长线上的点，且AD=AC，连接CD，求解△BCD面积的最大值.

解 因为∠BAC=120°，AD=AC，

所以∠BDC=60°，

因为△BCD是定边定角三角形，BC=6，

所以点D在△BCD的外接圆上移动，如图4所示.

当D移动到优弧BC的中点D′时，到BC的距离最大，此时△BCD的面积最大.

因为此时△BCD′是等腰三角形，

所以∠BD′C=60°，

所以S△BCD=3/4×62=93.

4 借助辅助圆，解决线段比或者面积比问题

例4在Rt△ABC中，AC=BC，∠ACB=90°，点P是CB延长线上的点，BP∶BC=k，已知0≤k≤1，经过点B作AB的垂线，过点P作AP的垂线，两条垂线的交点为Q，且AP=PQ，连接AQ，求△ABC与△APQ的面积比.

解 以AQ作为直径，AQ的中点O作为圆心，构建辅助圆，如图5所示.

5 结语

初中数学解题中，辅助圆是广泛应用的技巧，借助辅助圆可以解决几何问题、代数问题等题目.在具体的解题中，需要深入分析题目，结合具体要求构建辅助圆，帮助学生明确解题思路，提高学生的解题能力.

参考文献：

[1]刘怀权.“构造辅助圆”在初中数学解题中的应用[J].数理天地（初中版），2022（12）：21-22.

[2]魏瑞宾.案例分析辅助圆在初中数学解题中的应用[J].名师在线，2019（26）：16-17.

[3]徐勤.辅助圆在中考数学试题中的应用[J].科学大众（科学中考），2022（04）：13-15.