默比乌斯与古罗马的默比乌斯环

梦隐

本期封面是德国数学家、天文学家默比乌斯（August Ferdinand Mbius，1790—1868）的画像。默比乌斯生于德国萨克森州的普福尔塔（Pforta），据说其家族与宗教改革领袖马丁·路德有关，他就读的普福尔塔中学出了许多名人，包括历史学家兰克（Leopold von Ranke，1795—1886）与哲学家尼采（Friedrich Wilhelm Nietzsche，1844—1900）。成年后的默比乌斯相继在莱比锡大学、哥廷根大学与哈勒大学学习，1815年在数学家普法夫（Johann Friedrich Pfaff，1765—1825）指导下完成了题为《恒星之掩星》的博士论文。普法夫也是大数学家高斯（Carl Friedrich Gauss，1777—1855）的导师，因此名义上默比乌斯与高斯师出同门；不过高斯比他大13岁，数学成就更是其他任何人都无法企及的。

实际上，1813年默比乌斯曾向高斯学习理论天文学，当时高斯已担任哥廷根天文台台长多年了。1816年，默比乌斯被任命为莱比锡大学的天文学与高等力学教授，直到1868年去世，他一直在这所德国第二古老的大学工作。同高斯一样，默比乌斯的表面身份是天文学家，然而他们两人的天文学工作都几乎鲜为人知，在数学领域却千古留名。以默比乌斯命名的数学概念或工具包括默比乌斯平面、默比乌斯变换、默比乌斯函数、默比乌斯配置、默比乌斯反演等，涉及射影几何、数论与拓扑学等多个数学分枝，但是最广为人知的还是他晚年发现的一种既简单又奇妙的拓扑结构，它可以通过把一个长条纸带旋转180°之后再将两端粘上制得，这就是被后人称为“默比乌斯带”或“默比乌斯环”的数学模型：这是只有一个表面的环状物，如果一只蚂蚁沿着默比乌斯环前行，它将永远走不到头；再假如这只蚂蚁有意识，它知道顺时针或逆时针方向是什么意思，但是游历一周返回出发点时却发现原先认识的旋转方向完全相反了。用拓扑学的术语讲，默比乌斯环是一个不可定向（non-orientable）的表面；实际上每个不可定向的曲面都包含一个默比乌斯环。

另一位叫利斯廷（Johann Benedict Listing，1808—1882）的德国数学家也提出了这一单面环带的几何模型，时间可能还要早几年，他也是“拓扑学”（Topologie）这一术语的提出者。不过默比乌斯环（或带）的叫法已经约定俗成，况且他研究这一题材的轨迹也更为清晰。为了准备参加法国科学院有关多面体几何理论的竞赛，默比乌斯曾考虑通过折叠与粘合三角形来逐步构造多面体，在这一过程中发现了单面曲面。在他身后出版的著作全集里，收录了一篇未曾发表的1858年文稿，其中包含了图1中那种扭转了3、4、5个半圈的环带：默比乌斯系统地分析了这类环带，发现旋转180°的次数如果是奇数，产生的环带只有单面；如果次数是偶数，则环带仍然具有正反两面。默比乌斯环还有很多特性，这里省略。

制作一个默比乌斯环是如此容易，很难想象没有人更早发现过它，只不过没有认识其数学内涵而已。的确，在利斯廷与默比乌斯之前，没有人从数学上去考察它。有趣的是，在意大利的古罗马时代遗迹森提农（Sentinum）的别墅中，人们发现了一幅公元200—250年前后制作的马赛克壁画，画面中央是罗马神话中的永恒时间之神，站在一条绘着黄道十二宫的环带之中，仔细观察，可以发现这是一条默比乌斯环。这件艺术珍品后来被德国人买走，从1828年起就在慕尼黑的古代雕塑博物馆展出。默比乌斯或利斯廷是否参观过这件艺术品就不得而知了。

封二图A就是这幅马赛克壁画。永恒时间之神的名字是Aion，有人翻译成“艾咏”或“艾永”，我则建议译作“爱永”，其形象通常是一个裸体男性，伴随象征死而复生的蛇或周而复始的轮环。图中的爱永站在一个象征时间轮回的默比乌斯环状的黄道带内，带面上镶着代表十二宫的图形（十二宫的顺序不够准确）。黄道环两侧各有一棵大树，左边的枝头似已结出果实，右边正在长出新叶。右侧地面上半卧的女子是罗马人的大地女神特鲁斯（Tellus），相当于希腊神话的盖娅（Gaia），围绕她的四名孩童象征一年中的四个季节。

古罗马壁画、雕塑乃至钱币上都有伴着黄道带的爱永形象，但是莫比乌斯环形状的图像可能仅此一件。封三图C是在法国发现的罗马时代马赛克拼嵌地板中的爱永形象，图中的黄道带不是默比乌斯环。

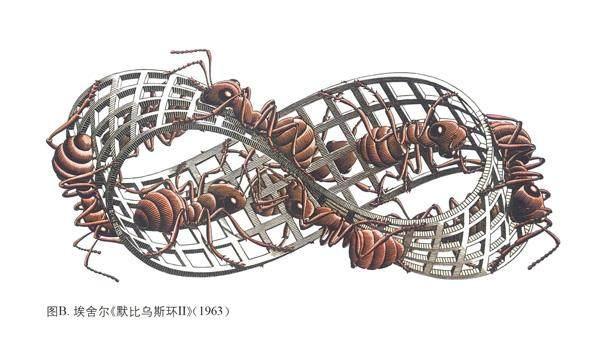
默比乌斯环引起许多艺术家的兴趣，最有代表性的就是荷兰画家埃舍尔（Maurits Cornelis Escher，1898—1972）了。封二图B和封三图D就是他的作品，深得科学家们的喜爱。李政道在《科学与艺术》一文中就引用了埃舍尔的《骑士》图，以此说明用艺术手法表达科学思想的意义。杨振宁则将它作为自己《基本粒子发现简史》（上海科学技术出版社，1963）的封面，借此阐释物理学中对称、互补与缔合变换等观念。

默比乌斯环给一些建筑师带来灵感，同时也成了一些装潢艺术家的素材，图2其实就是默比乌斯1858年手稿中那个压扁了的默比乌斯环，现已成为国际公认的回收循环利用标志，有许多不同的变体。

使用皮带轮作为传动设置的工匠可能早就发现并利用了默比乌斯环的性质，因为将长条皮带扭转半圈后再联结起来，带子的两面都会接触到旋转的轮子，磨损的速度只有正常安装形式的一半；此外，这种形式的传动带也不太容易左右卷曲。对于这种技术的早期文字记录可以追溯到1871年，那是在莫比乌斯的著作出版之后；不过中世纪穆斯林伊斯梅尔·贾扎里（Ismail al-Jazari，1136—1206）的一幅绘图手稿中就出现了默比乌斯环状配置的链条泵图像。

默比乌斯环也经常出现在科幻小说、电子游戏与影视作品中，通常的梗子就是把宇宙想象成如同默比乌斯环那样的构造，如《黑暗之墙》。1950年，美国天文学家多伊奇（Armin Joseph Deutsch，1918—1969）发表了一篇科幻短篇《一个叫做默比乌斯的地铁线》（A Subway Named Mobius），描繪波士顿地铁开辟了一条按照默比乌斯环设计的新线路，进入这条线路的波士顿MTA86号列车失踪了，系统管理者搞不明白它如何消失了，更无法解释它好像仍消耗电力在系统里运行。2019年美国华特迪斯尼推出的《复仇者联盟4：终局之战》（Avengers： Endgame）中，大英雄托尼·斯塔克（Tony Stark）尝试借由莫比乌斯环模拟时空拦截与时间指向，竟然获得成功。

参考资料

［1］ 李国伟. 默比乌斯把纸带转了几圈［A］. 李国伟. 数学文化揽胜集（艺数篇）［M］. 北京： 高等教育出版社， 2004．