有理分式函数的对称复极点的留数
丁明玲, 肖祥春, 李 薇
(1.福建农林大学 计算机与信息学院,福州 350002; 2.厦门理工学院 数学与统计学院,福建 厦门 361024)
0 引 言
留数定理及推广的留数定理[1]是计算闭合路径复积分的重要工具,同时也为数学分析无法或难以处理的一些实的定积分及广义积分提供有效的计算方法[1-4].复变函数在三大类孤立奇点(可去奇点、极点及本性奇点)的留数的计算规则与方法很多,但对于其中的极点,特别是级数较高的极点,其留数计算往往较为复杂.而有理分式函数是常见的复变函数,其孤立奇点多以关于坐标轴或原点对称的形式出现,但目前关于有理分式函数(特别是复系数有理分式函数)对称极点的留数的研究很少.
本文主要研究复系数有理分式函数在各类对称极点的留数之间的关系:有理分式函数的某一种形式的对称极点的留数之间是否也存在某种对称性?结合有理分式函数的奇偶性给出相应的结论.这些结论为有理分式函数对称极点的留数以及有理分式函数在闭合路径上的复积分提供了新的简便计算方法.
1 预备知识
定义1设
P(z)=a0zn+a1zn-1+…+an-1z+an,Q(z)=b0zm+b1zm-1+…+bm-1z+bm,
其中ai,bj∈,i=0,1,2,…,n,j=0,1,2,…,m.a0≠0,b0≠0,且Q(z)≠0,则称
为复系数有理分式函数.
特别地,若ai,bj∈,i=0,1,2,…,n,j=0,1,2,…,m,则称
为实系数有理分式函数.
引理1[1]如果z0是复变函数f(z)的k级极点,k为正整数,则
引理2[5]设f(z)是不恒为零的解析函数,则z0是f(z)的k级零点的充要条件是
f(z)=(z-z0)kφ(z),
其中φ(z)在点z0处解析,且φ(z0)≠0.
引理3[1]z0是函数f(z)的m级极点的充要条件是f(z)在z0点的某空心邻域0<|z-z0| 其中φ(z)在z0点解析,φ(z0)≠0. 引理5[6]设 是实系数有理分式函数,则R(k)(z)仍是实系数多项式,且 引理6[7]设复变函数f(z)在区域D内解析,则f(z)在D内有任意阶导数. 引理7设复变函数f(z)是解析函数,则在对于任意k∈, (i) 若f(z)是奇函数,则f(2k)(z)是奇函数,f(2k+1)(z)是偶函数; (ii) 若f(z)是偶函数,则f(2k)(z)是偶函数,f(2k+1)(z)是奇函数. 证若f(z)为解析函数,则由引理6,对任意k∈,f(k)(z)都存在. (i) 若f(z)是奇函数,则f(-z)=-f(z),从而f′(-z)(-1)=-f′(z),即f′(-z)=f′(z),因此f′(z)是偶函数. ① 当k=0时,显然f(2k)(z)=f(z)是奇函数,f(2k+1)(z)=f′(z)是偶函数. ② 假设当k=m∈+时,结论成立,即f(2m)(z)是奇函数,f(2m+1)(z)是偶函数,则 f(2m+1)(-z)=f(2m+1)(z), 从而 f(2m+2)(-z)=-f(2m+2)(z), 即f(2m+2)(z)是奇函数. 类似可证 f(2m+3)(-z)=f(2m+3)(z), 即f(2m+3)(z)是偶函数.因此当k=m+1时,f(2k)(z)是奇函数,f(2k+1)(z)是偶函数. 由数学归纳法,可得对任意k∈,若f(z)是奇函数,则f(2k)(z)是奇函数,f(2k+1)(z)是偶函数. (ii) 若f(z)是偶函数,类似(i)的证明可得f(2k)(z)是偶函数,f(2k+1)(z)是奇函数. 引理8[1]设复变函数 其中P(z),Q(z)在z0处解析,若P(z0)≠0,z0是Q(z)的一级零点,则z0是f(z)的一级极点,且 文献[6]给出关于实系数有理分式函数的共轭k级极点的留数的关系. 定理1[6]设 注1 由定理1知实系数有理分式函数在关于x轴对称的k级极点的留数也关于x轴对称.该结论是否适用于一般的复系数有理分式函数?答案是否定的. 例如,设复系数有理分式函数 由于i与-i都是R(z)的一级极点且关于x轴对称,由引理1,得 对于其他类型的对称极点,有理分式函数的留数是否也具有一定的对称性?下面分别就关于y轴对称,原点对称的极点给出有理分式函数的留数之间的关系. 定理2设 (1) 其中 则 (2) 类似可得 (3) 另由(2)式及引理4,有 (4) 下面对k分两种情形讨论: 情形1若k为奇数,则由(3)式,引理7与(4)式,有 情形2若k为偶数,则由(3)式,引理7与(4)式,有 解实系数有理分式函数 为奇函数,且在复平面上有两个关于y轴对称的二级极点-1与1.由引理1,有 注2 由定理2知,具有奇偶性的实系数有理分式函数在关于y轴对称的k级极点的留数也具有相应的对称性.若实系数有理分式函数是奇函数,则其在关于y轴对称的k级极点的留数关于x轴对称;若实系数有理分式函数是偶函数,则其在关于y轴对称的k级极点的留数也关于y轴对称.但定理2结论对于一般的复系数有理分式函数并不成立. 例如,复系数有理函数 是偶函数.R(z)在复平面上有两个关于y轴对称的一级极点-1与1.由引理1,有 定理3设 (5) (6) (7) 定理4设 为复系数有理分式函数.若α与-α都是Q(z)的k级零点,但不是P(z)的零点,则α与-α都是R(z)的k级极点,且 (i) 若R(z)是奇函数,则Res[R(z),-α]=Res[R(z),α]; (ii) 若R(z)是偶函数,则Res[R(z),-α]=-Res[R(z),α]. 证若α与-α都是Q(z)的k级零点,则 Q(z)=(z-α)k(z+α)kH(z), 且H(α)≠0,H(-α)≠0,从而 (8) 其中 于是 (9) 类似可得 (10) (i) 若R(z)是奇函数,则R(-z)=-R(z).再由式(8)式,可得 从而w(-z)=-w(z),即w(z)是奇函数. 下面对k分两种情形讨论: 情形1 若k为奇数,则由(10)式,引理7与(9)式,有 情形2 若k为偶数,则由(10)式,引理7与(9)式,有 综上,若R(z)是奇函数,则Res[R(z),-α]=Res[R(z),α]. (ii)若R(z)是偶函数,则R(-z)=R(z).类似情形(i)的证明,可得w(z)是偶函数,并进一步对k分奇数,偶数两种情形讨论,可得Res[R(z),-α]=-Res[R(z),α]. 注4 由定理4知,若复系数有理分式函数是奇函数,则其在关于原点对称的k级极点的留数相等;若复系数有理分式函数是偶函数,则其在关于原点对称的k级极点的留数也关于原点对称. 又R(z)是偶函数,由定理4(ii),得 由定理2(ii),得 由定理4(ii),得 由定理1得 再由留数定理得 对于级数较高的极点,利用传统的留数计算公式计算留数一般较繁琐.本文进一步举例说明运用上述结论可在一定程度上简化有理分式函数的对称极点留数的计算,并结合留数定理为闭合路径上的有理分式函数的复积分计算提供一种简便计算方法. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.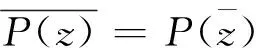

2 有理分式函数的对称极点的留数之间的关系
2.1 有理分式函数关于x轴对称的极点的留数的关系

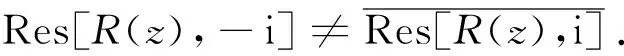
2.2 有理分式函数关于y轴对称的极点的留数的关系

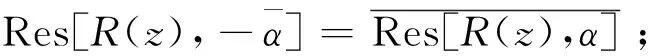
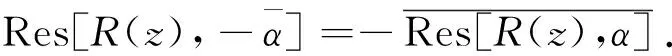

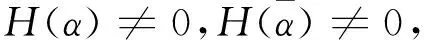

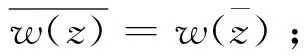
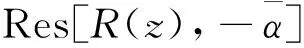


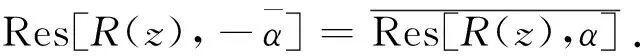













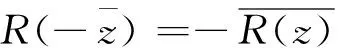
2.3 有理分式函数关于原点对称的极点的留数的关系

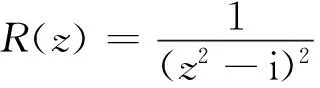

3 综合应用举例

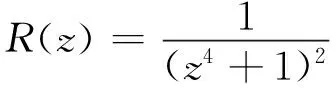
4 结 论