再谈构造法求an+1=kan+f(n)型递推关系数列的通项

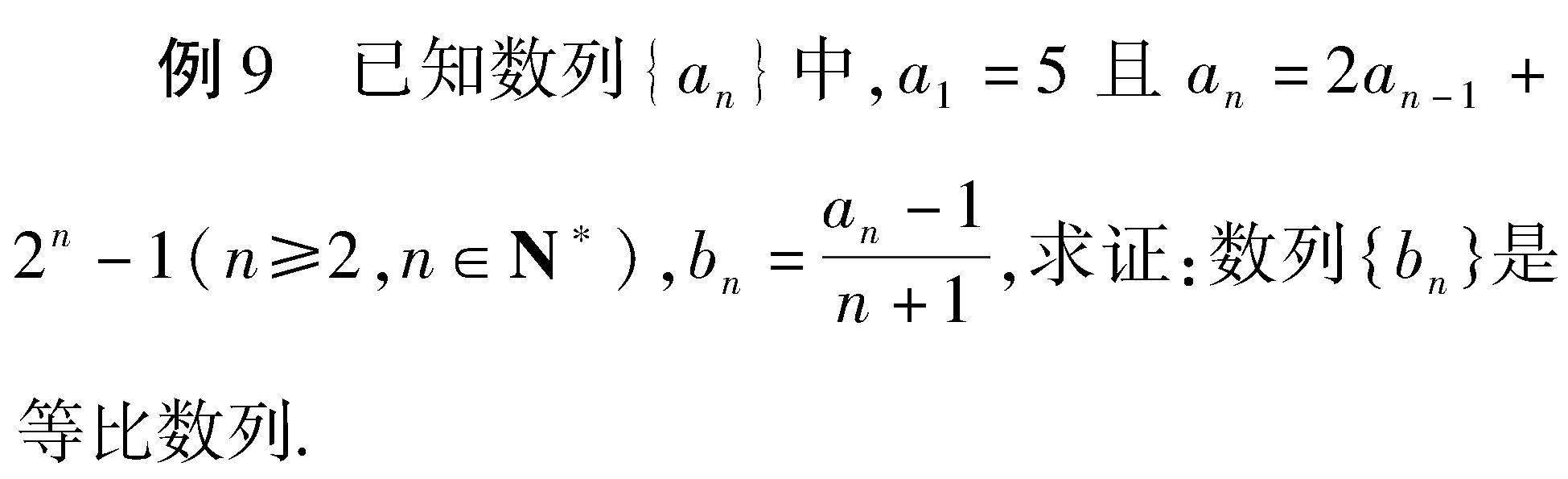
摘 要：针对an+1=kan+f（n）型递推关系，以系数k是否为1和f（n）的类型为标准，以构造等差数列、等比数列和常数列为基本途径，借助等差数列和等比数列的通项公式，实现求数列通项公式的目的.

关键词：数列；递推关系；通项公式；构造法

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0053-04

数列递推关系是考查学生探究能力的重要载体，探究数列的性质，探究如何求数列的通项.在解答题中，担心学生能力不足，命题者一般会设置解题坡度，学生只需按图索骥就能解决问题.但这并不影响我们对递推关系的研究，从简单到复杂，不断开拓视野，提升学生应变和解决问题的能力.形如an+1=kan+f（n）的递推关系是一类比较常见的问题，如何求数列的通项公式，方法是多样的.下面以系数k为第一分类标准，分别讨论f（n）的常见类型，统一采取构造法，实现求数列通项的目的.

1 系数k=1的类等差型

an+1-an=f（n）是等差数列定义的升级版.当

f（n）为常数时，递推关系表明{an}就是等差数列，直接套用公式就可以得到通项.下面主要考查f（n）不为常数的情形.

1.1 f（n）为一次式，构造常数列求通项

例1 在数列{an}中，a1=1，an+1-an=7-2n，求数列{an}的通项公式.

分析 我们知道，当f（n）是关于n的一次式时，通常采取叠加法求数列的通项.如果能将f（n）改写成某个数列相邻两项之差，则递推关系重组后出现相邻两项相等，从而得到一个常数列.设7-2n=g（n+1）-g（n），显然，当g（n）是关于n的一次式时，g（n+1）-g（n）为常数，不符合条件，这时必需“升级”g（n）为常数项为0的二次式[1].

解析 由an+1-an=7-2n，可设

an+1-［k（n+1）2+b（n+1）］=an-（kn2+bn）.

则an+1-an=［k（n+1）2+b（n+1）］-（kn2+bn）=2kn+k+b.

所以2kn+k+b=7-2n，

解得k=-1，b=8.

则an+1-［-（n+1）2+8（n+1）］=an-（-n2+8n）.

故数列an-（-n2+8n）是常数列.

所以an-（-n2+8n）=a1-（-1+8）=-6.

则an=-n2+8n-6.

小结 叠加是差为一次式的递推关系求通项的通法，虽然构造法看起来“复杂”，但如果差是二次式或更高次，除了需要应用特殊公式（如前n个正整数的平方和公式）外，构造应该是比较合理又好操作的方法.一般利用相邻高次式相减得低次式，待定系数完成多项式的“分配”[2].

1.2  f（n）为指数式的倍数，构造常数列求通项

例2 设数列{an}满足a1=2，an+1-an=3·22n-1，則an=.

分析 由于同底数的高次幂减低次幂，结果为低次幂，因此，将指数幂的倍数分解给an+1和an，只需要配置一个系数即可.

解析 由an+1-an=3·22n-1，

设

an+1-k·22n+1=an-k·22n-1，

则an+1-an=k·22n+1-k·22n-1

=3k·22n-1.

所以k=1.

即an+1-22n+1=an-22n-1.

所以数列an-22n-1是常数列.

从而an-22n-1=a1-2=0.

即an=22n-1.

1.3 f（n）为指数式加常数，构造等差数列求通项

例3 在数列{an}中，a1=1，an+1-an=2n+1，则数列{an}的通项公式是.

分析 通过叠加，借助等比数列前n项和公式是可以确定数列的通项公式，但由于指数式可以对应分解成相邻两项的差，因此可以构造一个等差数列.

解析 因为2n=2n+1-2n，

所以由an+1-an=2n+1可得

（an+1-2n+1）-（an-2n）=1.

则数列an-2n是公差为1的等差数列.

因为a1-2=-1，

所以an-2n=-1+（n-1）=n-2.

则an=2n+（n-2）.

1.4 f（n）为指数式加一次式，构造常数列求通项

例4 若a1=1，an+1-an=2n-n，n∈N*，则an=.

分析 虽然叠加法可求通项，但这是类型1和2的合并，因此可以构造常数列求通项.

解析 因为2n=2n+1-2n，且

所以由an+1-an=2n-n，可得

2 系数k≠1的类等比型

当系数k不等于1时，递推关系是等比数列的升级版.

2.1 f（n）为常数，构造等比数列求通项

例5 已知数列{an}中，an+1=4an-6，则an=.

列的首项.如果首项是0，则所有项都为0；如果首项不为0，则新数列为等比数列.求出an+m的通项，就可以得到数列{an}的通项公式.

解析 由an+1=4an-6，得

an+1-2=4（an-2）.

当a1-2=0，即a1=2时，由递推关系得an-2=0，所以an=2；

所以an-2是首项为a1-2，公比为4的等比数列.

因此an-2=（a1-2）·4n-1.

即an=（a1-2）·4n-1+2.

显然a1=2时也符合上式.

因此，an=（a1-2）·4n-1+2.

2.2  f（n）为一次式，构造等比数列求通项

例6 已知数列{an}满足a1=5，an+1=3an-4n+2（n∈N*）.数列bn满足bn=an-2n，则数列bn，{an}的通项公式分别为.

解析 由an+1=3an-4n+2，得

an+1-2（n+1）=3［an-2n］.

即bn+1=3bn.

因为b1=a1-2=3≠0，

所以数列bn是首项为3，公比为3的等比数列.

所以bn=3n.

从而an=3n+2n.

评析 为求数列{an}的通项公式，需要对数列递推关系式进行重构.设置数列bn，既是解题梯度，也是构造方向.为了“处理”掉一次项，相对于系数为1的递推关系，为什么是一次式而不是二次式，主要原因就在于系数.由于an+1和an两项的系数不相等，因此相邻一次项的差运算后就不会抵消掉一次项.故只需设an+1-［k（n+1）+b］=3［an-（kn+b）］，待定系数得到f（n）的分解，即an+1-2（n+1）=3（an-2n）[3].

2.3 f（n）为指数式，指数式的底数与系数相等，构造等差数列求通项

例7 已知数列{an}中，a1=1，an+1=3an+3n，则an=.

则an=n·3n-1.

2.4 f（n）为指数式，指数式的底数与系数不相等，构造等比数列求通项

例8 数列{an}中，已知a1=26，an=3an-1+2·5n（n∈N*，n≥2）.求证：数列an-5n+1是等比数列.

分析 当系数和幂底数不相等时，指数幂的转化有两种方式，一是同时除以幂，转化为线性递推关系，两次转化求解；二是分解幂，直接得到等比结构.

证法1 （同除构造）等式an=3an-1+2·5n两边同时除以5n，得

证法2 （分解构造）设an-k·5n+1=3（an-1-k·5n），则an=3an-1+2k·5n.

所以k=1.

又a1-52=1，

所以an-5n+1是公比为3的等比数列.

所以an-5n+1=3n-1.

即an=5n+1+3n-1.

2.5 f（n）為指数式加常数，构造等差数列求通项

证明 依题意，得an-1=2（an-1-1）+2n.

小结 由于系数和幂底数相等，先处理常数，再采取同除构造法比较简单；如果系数和幂底数不相等，先分解指数幂，转化为线性递推关系，再处理常数.

至于说f（n）的其他结构如分式，构造方式大同小异，本文不再赘述，读者可自行参阅相关文献.

3 结束语

关于an+1=kan+f（n）型数列递推关系，系数k为1是等差数列升级版，系数不为1则是等比数列的升级版.等差型递推关系一般采取叠加法，仅仅只能解决f（n）为一次式或可裂项的分式结构，等比型递推关系一般采取累乘法，解决的类型也不多.以等差和等比数列的定义为核心，基于构造法，通过改变递推关系式的结构，巧妙构造等差（常）数列和等比数列，实现求通项公式的自由.

参考文献：

［1］李秀元，夏志超.升幂裂项法在数列中的应用[J].中学生数学，2017（01）：19.

[2] 李秀元，夏志超.例谈构造常数列求通项公式[J].数理化解题研究，2016（25）：18.

[3] 李秀元.an+1+an=f（n）型数列问题的求解策略[J].数理天地（高中版），2021（03）：14-16.