某埋头弹机枪拨弹杠杆动力学分析及优化
刘 强, 周克栋, 李东昊, 陆 野, 赫 雷, 任海钺
(1.南京理工大学 机械工程学院, 南京 210094; 2.国营第二九六厂, 重庆 400050)
某埋头弹机枪采用了弹膛与枪管分离的摆膛机构,用以发射塑料弹壳的埋头弹。为了实现该枪的发射功能,将该枪后坐过程中的机构动作依次安排为开锁、摆膛、抽动推弹杆、输弹,其中输弹动作是本枪械后坐过程中的最后一个机构动作,前面三个机构动作在完成过程中消耗的自动机行程均很长,且四个机构动作必须依次完成,相互之间不能有交叠部分。考虑到全枪总长有限,故该枪在完成输弹过程中,主动件枪机框的行程很短,如不对输弹机构进行优化设计,则输弹机构难以平稳运行。因此,本文对拨弹杠杆曲线槽理论轮廓线进行优化设计,并对输弹机构的动力学特性进行分析。
对于传统机枪输弹机构的设计及动力学分析,前人已经做了很多研究及优化,王瑞林等[1]出于对某机枪人机功效的考虑,为了降低枪械首发装填的阻力,优化了某机枪输弹机构的大杠杆曲线;靳天佑等[2]以输弹机构在输弹过程中消耗自动机的动能为目标函数,求出了拨弹杠杆的最优解;姜奥等[3]通过优化输弹机构的传速比,减少了拨弹滑板的加速度;李洪强等[4]详细研究了输弹过程中输弹阻力的变化规律;李世康等[5]选用5次函数曲线优化了高射速转管炮的凸轮曲线,但他仅用到了五次函数曲线的平滑性,并未从机构力学特性入手,优化5次函数曲线。本枪所面临的主要矛盾与前面所述文献不同,需要在更短行程内完成输弹动作,传动件相互撞击接触力更大,工况更为恶劣。
1 输弹机构结构特点
本枪采用了凸轮杠杆的拨弹方式,输弹机构如图1所示。
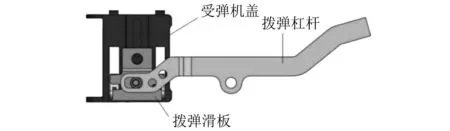
图1 输弹机构Fig.1 Feed transfer mechanism
本枪械所采用的输弹机构即传统的单程输弹机构,在枪机框后坐时,由枪机框上的导柱带动拨弹杠杆回转,拨弹杠杆带动拨弹滑板平动完成输弹动作。
在研究过程中,发现本枪械拨弹杠杆中实际起到拨弹作用的曲线槽部分很短,这是埋头弹枪拨弹行程过于靠近枪机框后坐结束所致。现将同口径88式5.8 mm通用机枪《自动循环图》[6]中的拨弹行程图部分与本文所述某埋头弹机枪对比,对比图如图2所示。

图2 拨弹行程对比Fig 2 Comparison of cartridge transferring travel
由图2对比可以看到,88式5.8 mm通用机枪枪机框后坐总行程160 mm,枪机框后坐位移到达39 mm时,即开始带动拨弹机构进行拨弹,整个拨弹行程达99.18 mm;而本文所述某埋头弹机枪枪机框后坐总行程130 mm,直到枪机框后坐位移到达81 mm时才开始拨弹,整个拨弹行程仅有38 mm。由于某埋头弹机枪的拨弹行程短,拨弹杠杆曲线部平均斜率大,故工况相较于88式5.8 mm通用机枪更为恶劣。
在最初采用直线段作为某埋头弹机枪拨弹杠杆曲线槽理论轮廓线(下文简称“理论轮廓线”)时,造成枪机框导柱进入杠杆曲线槽时对输弹机构的冲击很大。这种冲击会造成三个不利影响:①枪机框导柱进入拨弹杠杆曲线槽的过程中,枪机框速度会急剧下降,造成枪机框后坐能量不足;②枪机框导柱对拨弹杠杆的冲击引起连锁反应,使得输弹机构其他相关零部件之间也产生冲击,造成输弹机构中较薄弱的零件过早达到使用寿命或直接被损坏;③枪机框导柱瞬间冲击拨弹杠杆,使得拨弹杠杆带动拨弹滑板瞬间移动,拨弹滑板上铰接的拨弹齿瞬间拨动输弹机座上的塑料弹壳埋头弹,可能造成弹壳外表面被撞伤,产生安全隐患。因此,输弹机构工作平稳,降低枪机框导柱进入拨弹曲线槽时对输弹机构的冲击,是优化理论轮廓线的关键所在。
2 优化目标的确定
在机枪实际发射过程中,需要扣合输弹机盖,此时受弹机座上还有弹链,弹链完全遮挡了拨弹齿、拨弹滑板等结构,因此无法用高速摄影设备记录输弹机构的运动曲线。但高速摄影可以拍摄枪机框的运动过程,从而得到枪机框的运动曲线。因此,关于输弹机构中拨弹杠杆、拨弹滑板的运动必须依靠试验、仿真相结合的方式得到,即将试验得到的枪机框速度曲线与仿真得到的枪机框速度曲线相互对比,当仿真结果在可接受的误差范围内时,可认为仿真获得了真实情况,此时,在试验中难以测得的数据可以从仿真结果中间接获得。
将本文所研究的埋头弹机枪夹持在固定枪架上,并进行射击试验,用高速摄影设备拍摄枪机框运动过程,提取出枪机框后坐速度—时间曲线,然后将该试验所得曲线与仿真得到的速度—时间曲线进行对比,对比如图3所示。
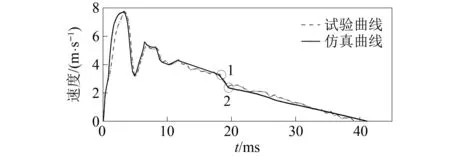
图3 枪机框速度实测、仿真对照Fig.3 Actual measurement and simulationcomparison of bolt carrier speed
图3中,实测速度—时间曲线与仿真速度—时间曲线的关键值对比如表1所示。

表1 枪机框速度—时间实测、仿真关键值对照
由表1可以看出,枪机框速度—时间曲线关键值的实测值与仿真值的误差≤5%,可以认为埋头弹机枪仿真结果较为真实地反映了枪机框实际运动的特点,因此可以将仿真得到的输弹过程中的关键数据提取出来,用于分析本埋头弹机枪输弹机构的动力学特性。图3中:枪机框速度到达点1时,枪机框导柱开始进入拨弹杠杆曲线槽;点1到点2的过程即枪机框导柱与拨弹杠杆曲线槽起始段相互撞击的过程。可见,在这个过程中,枪机框速度有所损失,损失为0.94 m/s。
因仿真较为准确地描述了枪机框的运动规律,可由仿真结果提取出枪机框导柱与拨弹杠杆曲线槽之间的相互作用力及拨弹杠杆的角速度—时间曲线、该作用力及枪机框速度—时间曲线。曲线如图4、图5所示。
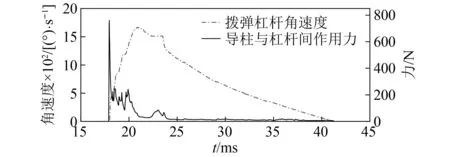
图4 拨弹杠杆角速度及导柱与拨弹杠杆间作用力Fig.4 The angular speed of the belt feed lever and the force between the guide post and the belt feed lever

图5 枪机框速度及导柱与拨弹杠杆间作用力Fig.5 The speed of bolt carrier and the force between the guide post and the belt feed lever
由图4、图5可以看出,枪机框导柱在进入拨弹杠杆曲线槽的一瞬间,与拨弹杠杆间作用力很大,为757 N,而后,在整个拨弹过程中,导柱与拨弹杠杆之间的相互作用力并不大,最高仅为200 N左右,这是由于枪机框导柱进入拨弹杠杆曲线段时,传速比突变引起的,因此,必须优化设计拨弹杠杆,使得枪机框导柱进入拨弹杠杆曲线时,传速比变化连续,且降低枪机框导柱对拨弹杠杆的冲击力。
本文对拨弹杠杆曲线槽的理论轮廓线进行优化,选取拨弹过程中导柱对拨弹杠杆的最大冲击力最小为目标函数,通过算法优化,寻求目标函数最小时对应的曲线槽理论轮廓线。
3 拨弹杠杆优化设计过程
3.1 优化参数的确定
基于枪械结构的约束,以及拨弹滑板运动行程的约束,理论轮廓线的起始坐标与终点坐标均已确定,优化的目的在于优化理论轮廓线的形状。由机械原理可知,凸轮理论轮廓线的形状决定从动件的运动规律,从动件常见的运动规律有:等速运动、等加速等减速运动、简谐运动、正弦加速运动、多项式运动规律等。根据以上运动规律,理论轮廓线形状的选取有多种方式,而多项式运动规律通用性较强,可以适应较多的运动特性。因此,本文采用五次函数曲线作为理论轮廓线的形式,五次函数曲线槽迫使运动件加速度连续,理论上不存在冲击[7],五次函数曲线的表达式为
(1)
式中:x1,y1为理论轮廓线上点的坐标;坐标原点O1在理论轮廓线的起始点,如图6所示。

图6 拨弹系统坐标系Fig.6 The coordinate system of the cartridge feeding system
因坐标原点在理论轮廓线的起始点,即理论轮廓线过(0,0)点,故式(1)中a0=0;又因为导柱进入拨弹杠杆曲线槽时,需要消除刚、柔性冲击,因此曲线在x1=0时,式(1)的一、二阶导数均为0,即,a2=a1=0。至此,待确定参数为a3~a5的值,因为输弹机构的结构参数已知,即五次函数曲线的终点坐标(p,q)已知,在曲线上再取两个点(p/3,y11),(2p/3,y12),y11与y12均为未知数,若知道y11、y12的值,就可由曲线终点坐标及所取两个点的坐标求解a3~a5的值,进而求出五次函数曲线的具体形式。
3.2 优化中的基本假设
本文对拨弹杠杆的优化将基于机构的动力学特性进行,为了建立相对准确的动力学模型,做出如下假设:
①枪机框导柱拨动拨弹杠杆的过程中,导柱与拨弹杠杆间的撞击普遍存在,本文将理论轮廓线离散为点集,并取两者间的撞击次数为曲线的离散点数,事实上,本文将拨弹杠杆曲线槽实际轮廓线离散为321个点,并对每个点上,枪机框导柱是否对拨弹杠杆造成冲击进行了判别,因此,这种处理方式较为准确地模拟了枪机框导柱与拨弹杠杆之间相互撞击的情况;
②撞击是瞬间完成的,在导柱对拨弹杠杆的撞击过程中,不考虑拨弹阻力及其他阻力对撞击的影响,所有阻力消耗的能量均在运动方程中考虑;
③撞击模型为纯弹性模型,不考虑撞击中的能量损失,撞击后,对撞物体可以瞬间恢复形变。
3.3 输弹机构接触分析
为了描述拨弹杠杆曲线槽实际轮廓线的形状,现建立坐标系(见图6)。
由图6可知,从枪机框上的导柱进入拨弹杠杆开始分析,在导柱截面圆心位置,即理论轮廓线起点O1位置建立定坐标系O1x1y1,x1轴指向为枪机框后坐方向。
在拨弹杠杆回转中心O2建立定坐标系O2x2y2,x2轴方向与x1轴平行。
在拨弹杠杆回转中心建立随动坐标系Ocxcyc,该随动坐标系与拨弹杠杆固连,在t=0时刻,Ocxcyc与O2x2y2重合。
假设导柱与拨弹杠杆的接触点为P,O1P与x1轴的夹角为φ,则P点在坐标系O1x1y1中的矢径为
R1=(s+r0cosφ,r0sinφ)T
(2)
式中:s为导柱位移,即枪机框位移;r0为导柱外圆半径。
假设O1到O2的距离矢量为R0=(-a,b),则P点在定坐标系O2x2y2中的矢径R2为
R2=R1-R0=(s+a+r0cosφ,r0sinφ-b)T
(3)
假设在t时刻,拨弹杠杆回转角度为τ,则在动坐标系Ocxcyc中,P点的矢径Rc为
Rc=ER2
(4)
式中,E为坐标变换矩阵,有
(5)
由以上诸式可以得到Rc的具体矩阵,矩阵中τ与s均为时间t的函数,知道τ和s的表达式,就可以知道拨弹杠杆曲线槽理论轮廓线的函数表达式。
由上述方法求出的曲线方程,为该类曲线的曲线族方程,要进一步确定曲线的具体形式,就需要确定φ与曲线形状的关系,即需要满足接触方程。由于导柱外圆与曲线槽曲线均光滑,根据微分几何包络理论,它们之间的接触方程为
R12·n1=0
(6)
式中,V12为凸轮轮廓曲线与导柱轮廓曲线之间的相对滑移速度,n1为导柱轮廓曲线在接触点的单位法向量,关于式(6)的详细计算过程,参见参考文献[7],由式(6)得
(7)
(8)
式中:v为枪机框后坐的平移速度;ω为拨弹杠杆摆动的角速度;s为枪机框位移;k为传速比,可以看出,具体到曲线上某点时,φ只与结构尺寸、枪机框位移及传速比有关,而传速比由理论轮廓线方程决定。
3.4 输弹机构运动分析
输弹过程中,除了枪机框、拨弹杠杆在运动,一起参与运动的还有拨弹滑板、弹链等零部件,为了研究拨弹滑板的运动,现对拨弹杠杆的尺寸标记如图7所示。
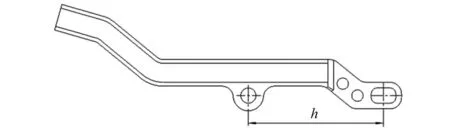
图7 拨弹杠杆尺寸标记Fig.7 Dimension marking of belt feed lever
在本枪械中,拨弹滑板只能做一个方向的平移运动,假设拨弹滑板的平移速度为vH,则有
vH=ωhcosτ=kvhcosτ=rv
(9)
式中:ω为拨弹杠杆摆动角速度;k为传速比;v为枪机框后坐速度;τ为拨弹杠杆摆过的角度,r=khcosτ。
在枪机框带动拨弹机构运动的过程中,符合能量守恒定律,根据能量守恒定律,可以列出枪机框及拨弹杆杆的运动方程为
(10)
式中:MA为枪机框质量;MB为从动件(包括拨弹滑板、拨弹齿、弹链)的质量;JB为拨弹杠杆的转动惯量;vA为枪机框位移为x时的速度;vA0为供弹阶段开始时枪机框的运动速度;PA为作用到枪机框上的火药燃气的压力;FA和FB为作用到枪机框和从动件上的阻力;ηp为传动效率;k0为供弹阶段开始时的传速比,k0=0;
ηp取常数0.8;FA为复进簧簧力,由复进簧参数求得;FB为拨弹阻力,从仿真结果读取。如若知道拨弹杠杆曲线段理论轮廓线的方程,即可知道枪机框导柱运动到曲线槽任意位置时的传速比,进而可由式求出枪机框在任意位置时的速度vA。
3.5 法向接触碰撞力模型
本文中采用Hertz接触理论计算导柱与拨弹杠杆相互碰撞时产生的碰撞力,该模型认为接触力是压入深度的非线性函数,且碰撞后参与部件可以弹性恢复,不存在能量损失,接触力表达式为[8]
Fn=Kδn
(11)
式中:δ为两个接触刚体之间的相对压入量;K为接触刚度系数;n为力指数,由接触刚体的材料和接触区域的几何特性决定,对于金属接触,n值取1.5。刚度K的计算式为[9]
(12)
式中:Ri与Rj分别为导柱的半径和导柱与拨弹杠杆接触点的曲率半径;σi、σj与导柱、拨弹杠杆的材料参数有关,其计算式为
(13)
式中,vl,El分别为材料的泊松比和弹性模量。
假设导柱每次与拨弹杠杆撞击以后,拨弹杠杆回转一个角度Δτ,即在曲线槽实际轮廓线第i点,导柱与拨弹杠杆撞击之前,拨弹杠杆的回转角度为τi-1,撞击之后为τi,有
Δτ=τi-τi-1
(14)
同理,在第i点发生撞击之前,枪机框后坐的速度为vAi-1,拨弹杠杆回转的角速度为ωi-1,拨弹杠杆上与导柱接触点的速度为vBi-1;发生撞击之后,枪机框后坐的速度为vAi,拨弹杠杆回转的角速度为ωi,拨弹杠杆上与导柱接触点的速度为vBi。枪机框导柱与拨弹杠杆之间的撞击就是枪机框为拨弹杠杆传速的过程。撞击前,拨弹杠杆在接触点Pi的速度方向如图8所示。

图8 拨弹杠杆与导柱接触点速度方向Fig.8 Speed direction of the contact point between the belt feed lever and the guide post

如图9所示,在Pi点,导柱与拨弹杠杆接触力的方向为O0Pi方向(见图6),在t=0时,O0与O1重合,O0为导柱圆心,O0Pi与枪机框后坐方向的夹角为φi,那么,拨弹杠杆上Pi点速度方向与O0Pi的夹角为αi+τi-1-φi,由Pi与O2的坐标求出O2Pi的长度为li,则此时导柱速度vAi-1与拨弹杠杆上Pi点的速度vBi-1在O0Pi方向的投影、分别为
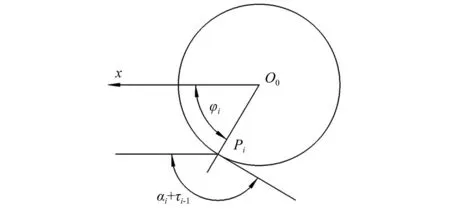
图9 接触点速度方向与接触力方向夹角示意图Fig.9 Schematic diagram of the angle between the speed direction of the contact point and the direction of the contact force
(15)
两者的差值即在Qi点的O1Qi方向,导柱相对于拨弹杠杆的速度
(16)
式中,若Δv>0,则为导柱撞击拨弹杠杆,撞击力由式(17)及式(11)计算;参见式(11),由能量守恒即可求出导柱与拨弹杠杆间的最大穿透深度μ
(17)
将求得的最大穿透深度μ代回式,则可以求出两者间的最大穿透力Fnm,即为所求撞击力。
式(16)中,若Δv<0,则为拨弹杠杆撞击导柱,撞击面不在所求面上,又因为拨弹杠杆质量远小于枪机框质量,拨弹杠杆对导柱的撞击力可以忽略不计,因此直接取Fnm=0,事实上,输弹机构在输弹过程中受到的阻碍更多,阻力大,质量小,因此,拨弹杠杆每次被导柱撞击后,撞击增加的速度很快就会降下来,一般不会出现Δv<0的情况。
3.6 优化过程
本文采用遗传算法[10]对所求的拨弹杆曲线槽理论轮廓线进行优化,其具体优化过程为:如2.1节所述,首先由遗传算法的赋值程序为y11、y12赋值,求出第一代五次函数曲线方程,并将该曲线离散为321个点。当枪机框导柱圆心处于第i点时,理论轮廓线与导柱圆心重合点Qi的坐标为(xi,yi),Qi到拨弹杠杆回转中心O2的距离为ji,但此时需要按照前一个重合点Qi-1求解出撞击前拨弹杠杆的回转角度τi-1,Qi-1到拨弹杠杆回转中心O2的距离为ji-1,τi-1如图10所示。

图10 拨弹杠杆回转角度示意图Fig.10 Schematic diagram of rotation angle of belt feed lever
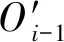
(18)
式中,b值为3.3节中所述b值。取导柱在第i-1(i≥3)点时,导柱与拨弹杠杆间的传速比为ki-1,有
(19)
将式(19)代入运动方程式(10),可以求出导柱在第i-1点完成传速后的后坐速度vAi-1及拨弹杠杆的回转角速度ωi-1,然后由2.5节中的方法,先求出理论轮廓线在i点的曲率半径,进而求出导柱与拨弹杠杆在i点的撞击力FNi,因为曲线被离散为321个点,除第一个点(第一个点传速比为0,回转角为0,默认无冲击)外,可以求出320个撞击力FNi(第二个点的冲击载荷由枪机框导柱进入曲线槽时的速度单独求出),取其中最大的一个撞击力值FNmax为一次计算的返回值,用遗传算法不断迭代,即不断更换五次函数曲线的方程,求FNmax的最小值,直至算法收敛,此时FNmax所对应的五次函数曲线即为所求的最优曲线。
4 优化结果
将优化后的结果与优化前的结果相比较,有拨弹杠杆曲线槽理论轮廓线的对比如图11所示。

图11 优化前后拨弹杠杆理论廓线展开线对比图Fig.11 Comparison of the theoretical profile of the belt feed lever before and after optimization
从图11可以看出,拨弹杠杆曲线槽起始段明显较为平缓,理论轮廓线斜率从0开始逐渐增大,使得枪机框导柱进入拨弹杠杆曲线槽时,理论上没有冲击。
按照图11所得的优化后理论轮廓线重新进行动力学仿真,得到枪机框速度-时间及导柱、拨弹杠杆间冲击力的曲线如图12所示。
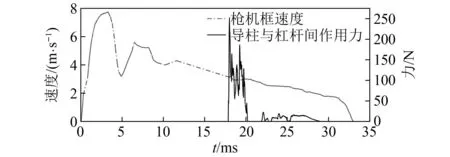
图12 优化后,枪机框速度及导柱与拨弹杠杆间作用力Fig.12 The speed of bolt carrier and the force between the guide post and the belt feed lever after optimization
按照图11所示理论轮廓线重新加工拨弹杠杆,并做射击试验,将两次试验得到的枪机框速度图线进行对比,对比图线如图13所示。
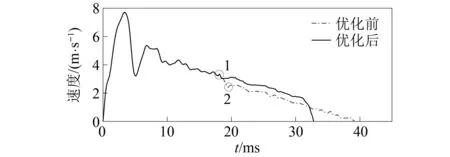
图13 拨弹杠杆曲线槽优化前后枪机框速度对比图Fig.13 Comparison diagram of the bolt carrier speed before and after the optimization of the curve slot of the belt feed lever
结合图13、图14及前文中的图3,在理论轮廓线优化前,枪机框导柱进入拨弹杠杆曲线槽时,速度从点1下降到点2,速度损失为0.94 m/s;优化后,该过程中,速度从点1下降到点3,速度损失为0.28 m/s。优化后的速度损失为优化前的29.79%。

图14 图13局部放大图Fig.14 Partial enlarged view of figure 13
将修改后的拨弹杠杆重新代入仿真计算,得到优化前后,枪机框导柱进入拨弹杠杆曲线槽时,导柱对拨弹杠杆的冲击对比,如图15所示。

图15 优化前后导导柱对拨弹杠杆冲击力对比Fig.15 Comparison of the impact force of the guide post on the belt feed lever before and after optimization
优化后,最大冲击力由优化前的757 N降低到了252 N,导柱进入拨弹杠杆曲线的冲击力约等于原来的1/3,可见,用控制碰撞力的方法,达到了优化的目的。
5 结 论
本文针对枪机框导柱进入拨弹杠杆曲线槽时冲击大,枪机框速度下降严重进行了研究分析,并对拨弹杠杆曲线槽的理论轮廓线进行了优化设计,利用枪械射击试验验证了优化结果的可信性及有效性,得出以下主要结论:
(1)通过建立动力学模型,可以较为准确地模拟枪械实际后坐过程,从而从仿真结果中提取出试验难以测量得到的数据。
(2)采用五次函数曲线作为拨弹杠杆曲线槽理论轮廓线的曲线形状有利于降低导柱进入弹膛螺旋槽时的冲击。
(3)通过将理论轮廓线离散为点集的形式,可以通过Hertz接触理论计算出导柱在每个点上拨弹杠杆曲线槽之间的撞击力,从而检索出导柱与曲线槽相互作用过程中的最大撞击力。
(4)通过遗传算法优化拨弹杠杆曲线槽理论轮廓线的具体形状,使导柱与曲线槽之间的最大撞击力最小,即得到本文所需要的最优曲线。按照最优曲线形状重新加工拨弹杠杆槽,并做试验,得出导柱在与拨弹杠杆曲线槽相互作用的整个过程中,枪机框速度损耗由优化前的0.91 m/s降低到优化后的0.28 m/s。并由仿真分析得出,优化后,导柱与拨弹杆杆曲线槽之间的最大冲击力降低为优化前的1/3,达到了优化目的。

