多轮廓线的三维形体重构技术研究与实现*
刘坤良,黄金明
(1.天津工业大学计算机科学与软件学院,天津 300387;2.中国地质调查局发展研究中心,北京 100037)
多轮廓线的三维形体重构技术研究与实现*
刘坤良1,黄金明2
(1.天津工业大学计算机科学与软件学院,天津 300387;2.中国地质调查局发展研究中心,北京 100037)
实际应用中,三维重构经常面对的不是直接的体数据信息,而是一序列的二维轮廓线数据,因此基于轮廓线的三维重构研究有着极其重要的实用价值。在多轮廓线的三维形体重构中,轮廓对应、轮廓拼接、分叉处理和末端轮廓线的封闭处理等是其关键技术。提出了三维重构中每一个实现步骤具体的解决方案。针对轮廓线绕向问题提出了夹角和检测法,有效避免了轮廓多边形的绕向误判;对轮廓线一对多分叉问题提出了按周长比率解决问题的思路;在末端轮廓线的三角剖分算法中提出了最大张角三角形方法,减少了三角剖分的计算量,达到了在各种形态轮廓线条件下能够实现正确的拼接。实现结果表明,轮廓线拼接过程中每个步骤的解决方法是正确有效的,相较于其他实现方法通用性更强。
轮廓线;三维重构;Delaunay三角剖分;凸包
1 引言
在实际应用中,我们可能常常面对的不是直接的体数据信息,而是一序列的二维轮廓线数据。从一组有序的平面轮廓线重建三维形体是一个具有普遍意义的研究课题, 在医学、地质、生物等领域有着非常广泛的应用。例如,在医学数据的可视化中,如果CT或者MRI图像两层切片之间的距离远远大于图像的分辨率,也就是Z方向的采样十分稀疏,这时需要在每层图像上就感兴趣的区域勾画出轮廓线,并由一序列的二维轮廓线重构出由面模型表示的三维形体。又如,在医学图像的三维数据场可视化中,尽管相邻断层图像之间的距离很小,但是目前的物质分类技术尚不能将共存的多种不同物质加以分类,需要人工干预,由医学专家手工勾划出感兴趣的区域,如在医学的治疗系统中,为了保证治疗的准确性和可靠性,先勾画出器官(血管、神经等)的轮廓线,再由这些轮廓线重建组织表面。如此,由器官轮廓线重建的组织表面可以极大限度地辅助医学诊断,为拟定最佳手术方案提供可靠的依据,从而提高手术质量,减少医疗事故[1]。因此,基于以上实际应用的需要,对三维重构的研究有着及其重要的实用价值。
基于轮廓线的三维形体重构需要解决轮廓线质心计算、轮廓线绕向调整、轮廓线对应、轮廓线拼接、轮廓线分叉以及末端轮廓线的封堵等相关问题。李运锋等[2]提出的基于方向包围盒投影转换的轮廓线拼接方案,首先判断多边形的顶点凹凸性,对于凹顶点,将其转换到对应的凸包上;然后计算凸包的方向包围盒,旋转平移矩形包围盒,并求包围盒内接椭圆,将每个顶点都按比例投影此椭圆上;基于投影后的点进行轮廓线拼接,寻找相邻轮廓线顶点之间的对应关系;最后还原实际坐标,进行原始模型的三维重构。该方案较之最短对角线方法,能比较好地解决最短对角线方法中出现拼接交叉的现象,但是由于该方案没有考虑轮廓线中心对齐问题以及轮廓线的尺寸变化,在一定情况下,也会发生扭曲现象,甚至投影转换后的模型,较投影之前,模型效果会更差,而且该方案也没解决轮廓线的分支问题。毛先成等[3]提出的复杂轮廓线三角面片的重构算法,虽然考虑了中心对齐以及轮廓线的尺寸变化,并提出了轮廓线分支的解决方案,但是,其处理分支问题时需要人工干预,降低了算法的自动性而且其没有处理末端轮廓线的封堵问题,在轮廓线末端出现空洞,使拼接结果不能形成封闭曲面。目前相关论文实现的轮廓线拼接方案,重点实现了轮廓线拼接过程中的某几个步骤,解决其中的几个问题,在其解决方案所面对的具体问题上能得到正确的解,但适用范围有限,通用性不强。
本文从轮廓线重构所需解决的问题出发,有效地解决了轮廓线拼接过程中出现的拼接交叉问题,实现了分支轮廓的自动处理以及末端轮廓线的封堵,多轮廓线的拼接结果满足工程需求。
2 轮廓线的预处理
对于中心点对齐、形状相近、绕向一致的相邻轮廓线,拼接结果一般不会出错。实际上,三维形体重构的轮廓线形态各异,为了提高重构的效果,避免错误的连接,有必要在轮廓线拼接之前进行轮廓线的处理。
2.1 轮廓线中心点对齐及尺寸调整
相邻轮廓线的形状和中心位置可能相差较大,必须通过坐标的平移和放缩,使相邻轮廓线转换成中心点重合、大小比例一致的轮廓线,才能正确地拼接处理[4],否则会产生锥体现象,如图1所示。

Figure 1 Incorrect splicing resulting in cones
假设相邻两轮廓线分别为Contour1和Contour2,其包围矩形的中心点坐标分别为center1(x1,y1)和center2(x2,y2),宽和高分别为(width1,height1)和(width2,height2),其中PanFactor和ZoomFactor分别表示轮廓线的平移距离和放缩因子,则有如下等式成立:

(1)
轮廓线Contour1各顶点坐标保持不变,Contour2各顶点的坐标作如下调整:
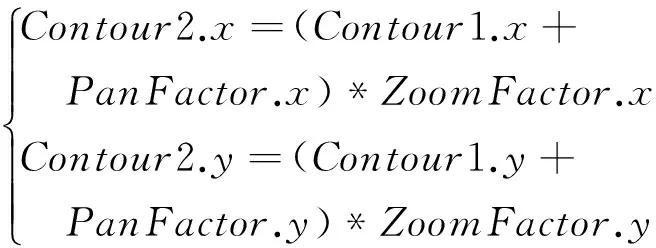
(2)
2.2 轮廓线绕向一致性调整
对于相邻的轮廓线在位置和尺寸调整以后,还需要判断轮廓线的绕向,如果轮廓线绕向不一致,要对其中一个轮廓线进行逆序处理。这些判断和处理是计算机图形学、模式识别、CAD等领域经常碰到的问题。大多数情况下,需要计算轮廓线的法向量,如果相邻轮廓线的法向量不一致,则轮廓线绕向不同,从而对其中一轮廓线进行绕向反向处理,这可以通过使轮廓线上控制点的顺序逆序来实现。由于轮廓线形态各异,轮廓线所形成的多边形有可能是凸多边形也可能是凹多边形,简单地计算轮廓线的法向量适用于凸多边形,当轮廓线是凹多边形时可能会得到错误的结果,其中一种解决办法是首先把凹多边形投影到其凸包上,然后计算其凸包的法向量,但这种方法增加了计算量。
本文采用夹角之和检测法检测轮廓线多边形的绕向问题,该方法对各种形态的轮廓线都能得到正确的结果,不需要计算凹多边形的凸包。轮廓线多边形的所有边均可看作有向边,边的方向与顶点的串连方向相一致。计算多边形每一条边与下一条边所形成的旋转角度之和,如果相邻两轮廓线的所有边形成的角度之和的值符号一致,那么它们绕向一致,否则绕向不一致。首先要确保轮廓线所在平面的法线向量方向一致,分别计算多边形前后两条边的叉乘和点乘,根据点乘结果可以得到两边的夹角,根据边叉乘后的向量与轮廓线所在平面的法向量比较结果取夹角值的符号,如果方向相同,夹角取正值,否则取负值,如图2所示。不管是凸多边形还是凹多边形,所有边形成的角度累积和或者接近2π或者接近-2π。其对应公式如下:
(3)
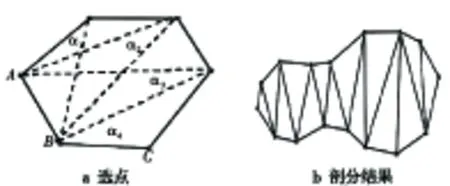
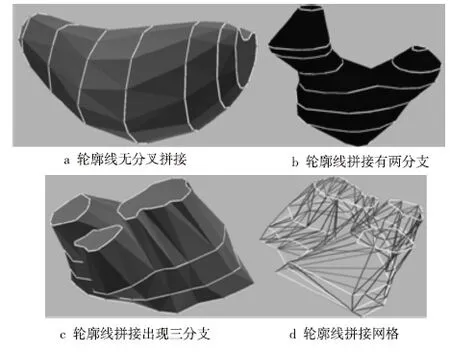
其中,Mi为两条边点乘结果,Ni为两条边叉乘矢量,Nface为轮廓线所在平面法向量。当Ni与轮廓线所在平面的法线Nface同向时Angle(i)取正,否则取负。0≤i Figure 2 Calculate deflection angles sum 2.3 轮廓线凸包计算及坐标到凸包的投影转换 对于凸轮廓线,可以采用轮廓线拼接技术直接拼接,而对于凹轮廓线,要先求其凸包,然后将凹顶点投影到其所在的凸包上。在矿体圈定的连接面积或者地层剖面中,轮廓线多边形通常都是凹多边形,因此必须进行凹多边形的凸化处理。 凸包是物体形状描述、特征抽取的一个重要工具,已被广泛地应用于模式识别、图像处理等研究领域。凸包的定义很简单,对于平面上的任意一个点集S,或者一个多边形P,其凸包是指包含S或P的最小的凸多边形[5]。 本文设计实现了轮廓线多边形的凸化处理算法,伪代码如下: voidCalConvexHull(V,n,S) input:轮廓线顶点集合V,顶点个数n output:轮廓线的凸包所包含的所有点集S { InitStack(S); Push(S,v0);Push(S,v1); k=2; a=v0;b=v1;c=vk; while(k!=1){ while(ConvexDeg(a,b,c)≤0&&(Top≥1)){ Pop(S); } a=S[Top]在V中的前驱顶点; b=S[Top]; c=S[Top]在V中的后续顶点; while(ConvexDeg(a,b,c)<0&&(Top≥1)){ V=V-vk; k=(k+1)%n; a=S[Top-1];b=S[Top];c=vk; while(ConvexDeg(a,b,c)>0){ V=V-vk; k=(k+1)%n; c=vk; } Pop(S); } Push(S,vk); } a=S[Top-1];b=S[Top];c=v1; if(ConvexDeg(a,b,c)<0) Pop(S); a=S[Top];b=S[1];c=S[2]; if(ConvexDeg(a,b,c)<0&&S[1]为V的第1个顶点) for(i=1;i s[i]=s[i+1]; } Pop(S); } 计算出凹轮廓线的凸包以后,对于轮廓线上的凹点,通过投影到最近的两个凸点的线段上,从而实现将一个任意形状的轮廓线映射为一个凸轮廓线。投影方式可以选择按比例投影或者垂直投影,由于垂直投影,投影后存在线段折回的现象,故本文中根据凹点到前一凸点的距离相对前后两个凸点在轮廓线上的距离之和的比值,选择按长度比例投影。该投影方法相较于垂直投影避免了线段折回造成的拼接交叉问题。 假设两相邻平行平面上各有一轮廓线,上轮廓线上的点列为p0,p1,…,pm-1,pm(其中pm与p0为同一点),下轮廓线上的点列为q0,q1,…,qn-1,qn(其中q0与qn为同一点),点列均按逆时针方向排列。每一个线段pipi+1或qiqi+1称为轮廓线线段。用一条轮廓线线段的两端点与相邻轮廓线上的一点相连接,可以构成一个三角面片,如图3所示。 Figure 3 Connecting control points 连接上轮廓线中的一点与下轮廓线中的一点的线段称为跨距。很显然,一条轮廓线线段,以及将该线段两端点与相邻轮廓线上的一点相连的两段跨距构成了一个三角面片,称为基本三角面片。而该两段跨距则分别称为左跨距和右跨距。实现两条凸轮廓线之间的三维形体重构就是要用一系列相互连接的三角面片将上、下两条轮廓线连接起来。但是,怎样保证连接起来的三维形体是合理的且具有良好的性质是需要认真研究的问题。连接上、下两条轮廓线上各点所形成的众多基本三角面片,应该构成相互连接的三维形体表面,而且相互之间不能在三角面片的内部相交。因此,只有同时满足下列两个条件的三角面片集合才是合理的: (1) 一个轮廓线线段必须在而且只能在一个基本三角面片中出现。因此,如果上、下两层轮廓线各有m和n条轮廓线线段,那么,合理的三维形体表将包含m+n个基本三角面片。 (2) 若一个跨距在某一基本三角面片中为左跨距,则该跨距必须是而且仅是另一个基本三角面片的右跨距。 将符合上述条件的三角面片集合称为可接受的形体表面。对于相邻两条轮廓线及其上的点列而言,符合上述条件的可接受的形体表面可以有多种不同的组合。在如此众多的可接受表面的组合中,为了确定所需要的一种组合,许多学者都通过制定不同的优化目标函数,提出了不同的优化方法。例如:FuchS H提出的表面面积最小法;Kepple E提出的体积最大法;Ehristiansen提出的最短对角线法;Ganapathy提出的相邻轮廓线同步前进法等[6]。其中,最大体积法、最短对角线法和相邻轮廓线同步前进法都属于启发式算法。表面面积最小法和体积最大法都属于全局最优的表面重构方法,计算量较大且较费时;而最短对角线法和相邻轮廓线同步前进法是属于局部最优的判定方法,计算量较小,可以提高计算速度。最短对角线法适用于上下轮廓线大小和形状相近,对中情况比较好的情况。该方法就是在四边形p1p2q1q2中的两条对角线p1q2和p2q1中选择较短的一条作为下一三角面片的边,生成三角面片,如图4所示。相邻轮廓线经过预处理后,大小、形状比较接近,对中情况也比较好,所以适合最短对角线法拼接。 Figure 4 The shortest diagonal algorithm 采用最短对角线法拼接相邻轮廓线时,从两轮廓线中控制点较少的轮廓线的第一个控制点p0开始,在对应轮廓线中查找离点p0距离最近的一点qi,以线段p0qi为起始边,执行最短对角线算法。 当相邻断层的轮廓线数目不等时要解决分支问题。对于多个不重叠的轮廓线而产生的分支问题,需要把多分支转化成一组单分支。轮廓线合并和轮廓线分裂是两个解决分支问题的方式,轮廓线合并是采用一定的方式把多条轮廓线合并为一条,再进行一对一的轮廓线拼接。而轮廓线分裂是采用一定的方式把单轮廓线分成多条轮廓线,再进行多个一对一的轮廓线的拼接。 4.1 内插边解决分支问题(分支数=2) 引入内插边来解决相邻轮廓线的分支问题属于轮廓线的分裂方法,它适用于独立分叉问题,该方法利用两轮廓线之间的垂直平分线将一断层的单轮廓线分成两条轮廓线,与另一断层两条轮廓线对应。 当多轮廓线间最短距离较大、上下轮廓线大小有较大的差别时,该方法会出现单轮廓线的大部分区域与相邻断层的一个较小的轮廓线相连,从而影响构造的精度,而且当分支过多时,该方法实现比较困难[7]。 4.2 按照周长比率解决分支问题(分支数≥3) 由于相邻断层距离较小,上下轮廓线的大小应该具有一定的相似性,可按照多轮廓线周长的比率把多分支问题转化成若干个单分支问题。设下层包含一条轮廓线,上层包含多条封闭轮廓线,需要把下层的单轮廓线按照上层多个轮廓线的周长的比率分裂成与上层轮廓线数目相同的多条轮廓线,然后按照上述步骤,进行轮廓线拼接[8]。设上层有三条轮廓线C1、C2、C3,下层有一条轮廓线C0。如图5所示,则实现轮廓线分裂的具体算法如下: Step 1 计算轮廓线C1、C2、C3的质点坐标,假设分别为B1、B2、B3,计算轮廓线C0的质点,假设为A0。 Step 2 计算以质点B1、B2、B3为顶点的多边形的质点,假设为B0。 Step 3 连接线段B0B1、B0B2、B0B3。 Step 4 轮廓线C0中做线段A0A1、A0A2、A0A3,分别平行于线段B0B1、B0B2、B0B3。 Step 5 计算轮廓线C1、C2、C3的周长,假设分别为P1、P2、P3。 Step 6 在轮廓线C0中计算点M1,使点M1把轮廓线C0中A1、M1、A2部分按照轮廓线C1、C2周长的比例分成两部分,即A1M1∶M1A2=P1∶P2。用同样的方法分别按照轮廓线C1、C3和C2、C3的周长的比率,把A1、M3、A3和A3、M2、A2各自分成两部分。 Step 7 把轮廓线C1、C2、C3分别和轮廓线C0分割后的三部分M1A0M3A1M1、M1A0M2A2M1、M2A0M3A3M2对应。 Step 8 按照单轮廓线的重构方法构建三维实体。 分裂之后的轮廓线在拼接前也要进行轮廓线数据的预处理。 Figure 5 Splitting when one line corresponds to multil-line 为了实现末端轮廓线的闭合处理,本文设计实现了任意多边形的三角剖分算法。该算法把轮廓线作为任意多边形,通过任意多边形的三角剖分算法,实现轮廓线的三角剖分。在实现任意多边形三角形剖分算法时,为了减少计算量,本文在搜索最小外接圆半径三角形时,采用最大张角三角形方法,即与当前边形成的夹角最大的点为待选点。如图6a所示,对于线段AB,轮廓线上其他顶点与该线段所形成的夹角分别为α1α2α3α4,其中α4值最大,故选取C点与线段AB组成一个剖分三角形。 Figure 6 Triangulating contour line 本文以VisualC++6.0和开放式3D图形编程接口OpenGL为开发工具。使用固体矿产资源开发领域中,二维反演生成的一系列二维轮廓线数据,进行轮廓线预处理、轮廓线拼接、分叉和末端轮廓线的封闭处理生成封闭的三维形体模型,如图7所示。 Figure 7 Contour lines splicing and triangulation result 从图7可以看出,各种形态的轮廓线所形成的三维模型拼接正确,有效避免了模型交叉等错误拼接现象。单对多轮廓线对应的情况,如图7b、图7c所示,对于一个轮廓线对应超过三个以上的轮廓线情况,该方法同样有效,能够自动实现单轮廓线按周长比例分割,完全避免了人工干预且分割结果符合工程需求。各种形态的末端轮廓线被看作任意形状的多边形,采用本文介绍的任意多边形剖分算法,其剖分结果如图7a、图7c、图7d所示,实现了末端轮廓线的闭合处理,不会出现空洞或剖分后三角形面的相交情况,其算法时间复杂度与文献[7]实现的三角剖分算法相同,约为O(N2)[9]。但是,在搜索最小外接圆半径三角形时采用本文的方法,可以减少计算量,因为计算半径需要开方,其计算量大,而最大张角三角形方法只需要乘除运算,并且在搜索候选点时,最小外接圆半径法由于计算精度问题,对工程中控制点坐标绝对值很大、相对值较小的情况,会造成剖分错误,出现空洞或剖分后的三角形面相交。 本文研究了多轮廓线三维形体重构中,轮廓对应、轮廓拼接、分叉和末端轮廓线的封闭等关键技术,提出了三维重构中每一个实现步骤具体的解决方案。针对轮廓线绕向问题,提出了夹角之和检测法检测轮廓线多边形的绕向问题,有效避免了绕向误判;轮廓线拼接过程中,首先把凹多边形投影于凸包上,然后进行轮廓线的拼接;对于轮廓线一对多分叉问题提出了按周长比率解决问题的思路;对末端轮廓线通过任意多边形的三角剖分算法实现曲面的封闭,三角剖分中,搜索具有最小外接圆半径三角形时,采用最大张角三角形方法,减少了三角剖分的计算量。实验结果表明,这些实现方法切实可行,相较于其他轮廓线拼接方法,过程直观易懂、速度快、通用性强。当轮廓线不平行时,可以在轮廓线预处理阶段相对某个参考点或者参考面转换为平行或近似平行的轮廓线[10],采用上述方法拼接完成后再转换为原始坐标获得正确的重构结果。今后,我们将研究不平行轮廓线间的三维形体重构及三维重构结果的平滑处理,使轮廓线重构算法更通用,重构结果更自然、美观。 [1]HuangYong-li.Theoryandtechnologyresearchof3Dreconstructionbasedonslice-imagesdata[D].Zhengzhou:ZhengzhouUniversity, 2004.(inChinese) [2]LiYun-feng,LiuXiu-guo.AlgorithmofcontourssplicingbasedonOBBprojectiontransformation[J].JournalofComputerApplications, 2011,31(12):3353-3356.(inChinese) [3]MaoXian-cheng,LuXiao-qin,XuZhi-qiang.Triangletilesreconstructionfromdrilldata-basedcomplexcontours[J].ComputerEngineeringandApplications,2009,45(23):179-181.(inChinese) [4]MaHong-bin,GuoJia-teng.Cut-and-sewalgorithm:Anewmulti-contourreconstructionalgorithm[J].JournalofNortheasternUniversity,2007, 28(1):111-114.(inChinese) [5]WuZhong-hai,YeCheng-qing,PanYun-he.AnImprovedalgorithmofconvexhullcomputing[J].JournalofComputer-AidedDesign&ComputerGraphics,1997,9(1):9-13.(inChinese) [6]TangZhe-sheng.Visualizationof3dspatialdatasets[M].Beijing:TsinghuaUniversityPress,1992.(inChinese) [7]TuZhi-hong,SangNong.DelaunaytriangulationalgorithmofarbitrarypolygonswithvisualClanguage[J].Computer&DigitalEngineering,2005,33(1):34-36.(inChinese) [8]LiMei,MaoShan-jun,MaAi-nai.Buildingorebodysolidmodelfromplanarcontours[J].JournalofComputer-AidedDesign&ComputerGraphics,2006,18(7):1017-1021.(inChinese) [9]ShuAn,RanShu-yang,WuZhang-wen,etal.Threedimensionalsurfacesreconstructionbasedonshapeofadjacentlayercontours[J].JournalofComputerApplictions,2009,29(2):450-452.(inChinese) [10]SeungWonShin,DamirJuric.Modelingthree-dimensionalmultiphaseflowusingalevelcontourreconstructionmethodforfronttrackingwithoutconnectivity[J].JournalofComputationalPhysics, 2002,180:427-470. 附中文参考文献: [1] 黄永丽. 基于断层数据的三维重建理论与技术的研究[D].郑州:郑州大学, 2004. [2] 李运峰,刘修国.基于方向包围盒投影转换的轮廓线拼接算法[J]. 计算机应用, 2011,31(12):3353-3356. [3] 毛先成,卢晓琴,徐志强.基于钻孔数据的复杂轮廓线三角面片的重构[J].计算机工程与应用,2009,45(23):179-181. [4] 马洪滨,郭甲腾.一种新的多轮廓线重构三维形体算法:切开-缝合法[J].东北大学学报(自然科学版), 2007, 28(1):111-114. [5] 吴中海,叶澄清,潘云鹤.一个改进的简单多边形凸包算法[J].计算机辅助设计与图形学学报,1997,9(1):9-13. [6] 唐泽圣. 三维数据场可视化[M]. 北京:清华大学出版社,1992. [7] 涂治红,桑农.用VC语言实现任意多边形的Delaunay完全三角剖分[J].计算机与数字工程,2005,33(1):34-36. [8] 李梅,毛善君,马蔼乃. 平行轮廓线三维矿体重建算法[J]. 计算机辅助设计与图形学学报,2006,18(7):1017 -1021. [9] 苏安,冉蜀阳,吴章文,等. 基于相邻层轮廓线几何形状匹配的三维重建[J]. 计算机应用,2009,29(2):450-452. LIU Kun-liang,born in 1976,MS,lecturer,his research interests include algorithms analysis and design, and 3D data visualization. Study and implementation of multi-contour 3D reconstruction LIU Kun-liang1,HUANG Jin-ming2 (1.School of Computer Science & Software Engineering,Tianjin Polytechnic University,Tianjin 300387;2.Development and Research Center,China Geological Survey,Beijing 100037,China) In practical applications, 3D reconstruction often faces a series of 2D contour lines rather than the volume data we often process, so studying 3D reconstruction based on contours has important practical values. The key technologies of 3D-reconstruction based on multiple contours include contours corresponding, contours splicing, crotched contours handling, and terminal contours closing . The concrete solutions to each step of 3D construction of contours are given. According to the winding direction issue of contours, we propose a method of gauging the sum of angles, avoiding error judgment of the winding direction of contours. For the crotching issue of one contour corresponding to multiple contours, we give a way of splitting contours based on the circumference ratio of corresponding contours. We also give the means of maximum angle in order to reduce the calculation time on triangulating terminal contours. The proposed solutions can achieve correct contours splicing of any contours, guarantee that each step of the solution is correct and effective, and they are more universal compared to other solutions. contour;3D reconstruction;Delaunay triangulate;convex hull 1007-130X(2015)01-0133-06 2013-04-10; 2013-07-04基金项目:中国地质调查局发展研究中心承担的“华南地区深部岩体圈定与形态研究”工作项目([2011]02-22-14)通信作者:黄金明(hjm89211@163.com) TP391.4 A 10.3969/j.issn.1007-130X.2015.01.020 刘坤良(1976-),男,山东金乡人,硕士,讲师,研究方向为算法设计与分析、三维可视化。E-mail:2003_asecliu@126.com 通信地址:300387 天津市天津工业大学计算机科学与软件学院 Address:School of Computer Science & Software Engineering,Tianjin Polytechnic University,Tianjin 300387,P.R.China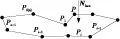
3 轮廓线的拼接


4 分支问题

5 末端轮廓线的闭合处理
6 实现结果
7 结束语


