面向CPU+MIC混合异构平台的地震波叠前时间偏移算法并行与优化策略*

熊 敏，王勇献

(国防科学技术大学计算机学院，湖南 长沙 410073)

面向CPU+MIC混合异构平台的地震波叠前时间偏移算法并行与优化策略*

熊 敏，王勇献

(国防科学技术大学计算机学院，湖南 长沙 410073)

地震波的叠前时间偏移算法是构造复杂岩层成像最有效的方法之一。地震勘探进入海量数据时代，且叠前偏移算法是数据处理中最费时的环节，对叠前偏移算法做并行计算优化有着重要的研究意义。近年来，高性能并行计算开始进入异构、众核时代，以Intel新一代至强融核MIC(Xeon Phi)为例，新型众核处理器具有成本低、性能高等特点。从最经典的Kirchhoff叠前时间偏移 (PKTM) 算法出发，基于CPU+MIC异构平台，采用offload编程模式实现对PKTM算法的并行移植与性能优化，对于6 000万规模(8 000×8 000)的应用问题，总的并行模拟时间从357.52 s减少到1.66 s，性能提升了214.37倍。

协同并行；Intel至强融核；异构并行；Kirchhoff叠前时间偏移；性能优化

1 引言

对地底岩层构造进行成像是石油、天然气勘探开发，以及地震勘探等领域的重要环节。地震波的叠前时间偏移算法是构造复杂岩层成像最有效的方法之一。Kirchhoff叠前时间偏移PKTM(Prestack Kirchhoff Time Migration)算法具有成像效率高、对速度模型要求低的优点，能适应纵横向速度变化较大的情况，同时还适用于大倾角的偏移成像，因此在构造复杂的地区，其优势更为突出。该算法自20世纪90年代起，逐渐成为地震勘探数据处理的常用成像手段[1]。图1显示的是PKTM算法的反演过程，图1a是地下模型空间，图1b数据空间，图1c是反演获得的模型空间，对于如汉字这样复杂的形状，PKTM算法仍然具有很高的还原度。随着地震勘探进入海量数据时代，对计算资源的需求日益增加，叠前偏移算法是数据处理中最费时的环节，对叠前偏移算法进行并行计算优化有着重要的研究意义。

Figure 1 PKTM migration process

近年来，高性能计算开始进入异构、众核时代，异构众核是大规模并行计算机的发展趋势，新型众核处理器具有成本低、性能高等特点。以Intel新一代至强融核MIC(Xeon Phi)为例，单个MIC设备拥有50个以上的处理器核，并采用宽向量(512位)设计，能够提供1 TFlops双精度浮点运算的性能，同时MIC还具有通用编程环境(Fortran、C 和 C++)、低功耗性能比、支持异构应用等优势[2]。Intel针对MIC推出一系列软件工具链，以支持基于MIC的软件开发，当前CPU+MIC异构平台主要有四种编程模式：CPU原生模式、CPU为主MIC为辅模式(又称offload模式)、CPU和MIC对等模式、MIC为主CPU为辅模式。最新TOP500[3]蝉联第一的“天河二号”超级计算机即以MIC作为加速部件。针对不同领域应用问题的模型和计算特点，结合MIC的体系结构特点，研究在该处理器平台上的性能优化已经成为当前的研究热点之一。

受益于硬件平台的不断更新与发展，地震波叠前时间偏移计算方法的性能在过去一段时间也持续获得较大的提升。Bhardwaj D等人[4]利用MPI实现叠前偏移算法优化，使偏移计算效率提高了近30%。王华忠等人[5]在集群系统中利用OpenMP多线程并行方法，优化了三维Kirchhoff积分法偏移实现方案。张清等人[6]利用CUDA编程模型在GPU平台上设计实现了静态8点并行插值算法，性能是CPU动态插值算法内核的22.76倍。随着MIC等新型众核系统的出现，如何在CPU+MIC的异构平台上，充分结合硬件体系结构特点与叠前时间偏移算法本身的特点，来做并行性能优化，仍是一个值得探索的问题。本文从最经典的Kirchhoff叠前时间偏移 (PKTM) 算法出发，基于CPU+MIC异构平台，采用offload编程模式实现对PKTM算法的并行移植与性能优化。

2 地震波叠前时间偏移算法

在经典的Kirchhoff叠前时间偏移(PKTM)算法中，定义了两个空间，一个是模型空间，简记为x-s空间，是对地底岩层构造的刻画，其离散下标记为(ix,is)；另一个为数据空间，简记为y-t空间，是对仪器成像数据的刻画，其离散下标记为(iy,it)。PKTM算法的实质是根据成像数据各像素的取值来反演、“复原”原始地底岩层构造的过程，具体来说，对于某个模型空间点(x,s)而言，按照成像原理与规律，若它会在数据空间内的点(y,t)处成像(该点未必唯一)，则需要满足式(1)：

(x-y)2=v2(t2-s2)

(1)

其中v是与波传播速度相关的一个常数。PKTM算法就是根据这一原理进行实现的，图2为经典PKTM算法的核心实现流程[7]，其优点是在复杂边界条件下仍然能保持计算稳定[8]。

Figure 2 Classical PKTM algorithm

图2 经典Kirchhoff叠前时间偏移(PKTM)算法流程

算法的主体部分是用一个三重循环操作data和modl两个数组，其时间复杂度为O(nx2×nt)，空间复杂度为O(nx×nt)。

3 移植和优化方法

根据PKTM的实现过程与计算特点，本文将从四个层次对PKTM算法进行移植和优化：算法层次的优化、串行程序性能优化、单一平台上的多线程并行以及CPU+MIC异构平台上的混合并行。

3.1 算法层次的优化

本文首先分析原始算法的时间复杂性，并尝试降低一个量阶时间开销的快速算法，基于新的快速算法探索进一步缩小迭代空间、提升加速效果的技术。

3.1.1 快速PKTM算法

由图2中的经典PKTM算法流程可知，该算法的核心是计算数组下标，其中当给定模型空间下标(ix,is)以及数据空间的第一维下标iy时，计算数据空间的下标it是最费时的部分，要用到加减乘除及乘方、开方、取整等运算，即:

t2=(x-y)2/v2+s2,it=[t/dt]

(2)

其中[ ]表示取整运算符。注意到计算t时等号右边第一项仅依赖于x与y的差值，因此若作变量替换ib=iy-ix，则可直接针对ib进行遍历，避免对(ix,iy)的组合进行遍历，从而达到降低遍历空间开销的目的。受此启发，Claerbout J F和Black J L在经典算法基础上进行改进，提出快速PKTM算法实现，流程如图3所示[5]。快速算法使核心计算部分集中在二重循环的内部，时间复杂度从经典算法的(nx2×nt)降低到了O(nx×nt)。

Figure 3 Fast PKTM algorithm

图3 快速Kirchhoff叠前时间偏移(PKTM)算法

3.1.2 提前确定迭代次数

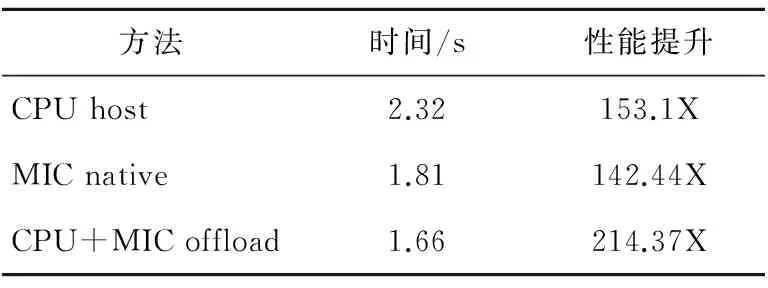
在图3的快速PKTM算法中，第6行有一个分支判断，以确定是否产生了有效的it下标值，且仅当it有效时才执行第7～9行的数据更新过程。由于第6行it有效性判定准则it

b2/v2+s2

(3)

注意到不等式左边为平方和的形式，它是变量b和s的递增函数，因此在第2～11行的循环迭代中，一旦某个ib值(不妨记为ibMax)导致第6行的it值越界无效，则后续更大ib值的迭代也同样产生无效的it取值，因此可直接跳过这些后续的ib迭代，从而避免后续迭代中冗余的it计算。事实上，也可预先计算能产生有效it值的ib迭代范围[0,ibMax)，达到同样的目的。提前判断出it的有效性也就是提前确定了迭代的次数，这种方法的好处是避免了无效it的计算，减少核心计算部分的计算次数。

为了有效量化这种技术带来的收益，先将公式(3)写成如下等价形式：

(4)

这表明在b-s平面(或者等价的整数坐标ib-is平面)上，能产生有效it值的范围是一个椭圆在第一象限和第二象限所包围区域的内部(图4中I所示)。图4中横轴表示ib的取值，纵轴表示is的取值，椭圆内部为满足公式(4)的范围，以nx和-nx为顶点的大矩形框内部表示图3第1～2行的全部迭代空间范围，本方法将ib的取值缩小到椭圆的顶点ibMax和-ibMax，两个矩形框之间的部分(图4中II所示)即为本方法所节约的迭代范围。以nx=8 000，nt=8 000，dt=0.004，dx=25，v=1 000为例，经过简单计算可知迭代空间大小从1.28×108减少为2.048×107，避免了约84%的无效迭代。

Figure 4 Ellipse relationship between variables ib and is

3.1.3 利用对称性减少迭代次数

观察图4，发现产生有效it的区域具有对称性，即图4中椭圆在第一象限和第二象限所包围区域左右对称，同时通过3.1.2节的方法优化后所确定的迭代范围也具有对称性，即与椭圆相切的矩形区域同样左右对称。考虑到公式(1)中计算t的过程用到的是b-s平面中点的坐标的平方值，而在对称区域中，对称点的坐标的平方值相同，因此可以利用此特性减少迭代次数以及核心计算的次数。图5为本方法的优化示意图，优化代码将ib=0的情况进行特殊处理，剩下的两个部分完全对称，ib的迭代范围缩小到(1,nx-1)，核心计算的次数也随之减半。

优化前 doib=-(nx-1),(nx-1) …if(it

优化后 doib=0,0 …(单独处理ib=0情形)enddodoib=1,nx-1 …(核心计算:计算it的值) if(it

Figure 5 Optimization method of symmetry to reduce loop cycles

图5 利用对称性减少迭代次数示意图

3.2 串行程序的性能优化

在算法层次进行优化之后，本文对于串行程序进行了一系列优化，包括优化计算和优化访存两个方面。

3.2.1 优化计算

(1)常量计算提前。

图3所示的快速Kirchhoff叠前时间偏移算法的流程中，第3～5行集中了平方、开方、除法和乘法等耗时的计算过程，是算法的核心计算部分。其中dx、dt、v、ds为常量，仅与常量相关与变量无关的计算只需要计算一次，就可以在每次迭代中使用，因此将这样的常量计算提前到循环外部，可以有效减少计算的次数。对于公式(2)中对it的求解可以改写成如下形式(ix-iy)：

(5)

改进前，除法运算和平方运算的运算次数约为4×nx×nt，而将常量计算提前后，除法运算的运算次数为1，平方运算的运算次数为2×nx×nt+2×nt+1。

(2)避免单双精度混合运算。

两种不同精度的数运算时，根据包容性，精度低的数需要先进行精度转换才能保证计算结果的正确性。如单双精度浮点数混合运算时，单精度浮点数将先转换成双精度数，然后再进行双精度浮点计算。而精度越高，运算的开销越大，因此如果仅使用单精度就能满足的运算，应当避免与双精度浮点数混合运算，从而减少高精度运算的额外开销。

快速Kirchhoff叠前时间偏移算法中的所有计算过程，利用单精度浮点计算就足以保证精度。在具体代码中，常常会用到一些浮点常量，如果没有显式标识为单精度浮点数，这些浮点常量将先被自动处理为双精度浮点数，然后再与单精度的变量进行混合运算。为了避免单双精度混合运算，应当在使用浮点常量时显式地将其标识为单精度浮点数。

(3)SIMD向量化。

现代CPU处理器指令集普遍支持以单指令多数据(SIMD)方式执行向量指令，充分利用好这些向量指令，可显著提高应用程序性能。例如，在IntelXeon处理器上支持256位宽的向量寄存器及相对应的AVX或AVX2向量处理的指令，而在新一代MIC处理器上则支持512位宽的向量寄存器及相应向量处理指令，这意味着理想情况下，MIC上的一条指令可以并发处理16个单精度浮点数(每个单精度浮点数4字节、32位)的操作，较单指令单数据的标量处理加速16倍。

为了在应用程序中充分进行SIMD向量化，可以通过编译器自动向量化、手工添加编译指导语句、使用库提供的向量数据类型编程、使用intrinsics编程以及内嵌向量化汇编指令等方式加以实现。为了在性能与程序移植性、可读性等方面达到平衡，本文主要采用重构程序、使用编译指导语句相结合以辅助编译器自动向量化的方式。主要技术包括：①对内层对称的ix迭代进行循环分裂，形成两个循环结构，为了利用编译器自动向量化，将其均修改为迭代变量逐次增加的形式；②在两个最内层循环上加上#pragmasimd以告诉编译器无需进行依赖性检测，从而生成向量化指令。

3.2.2 优化访存

访存是并行程序获得良好并行效果的重要因素之一，并行程序的执行过程中，由于循环变量有一定先后顺序，可能出现访问数据的顺序与数据存放的顺序不一致的情况，造成访存局部性不好，发生访问内存不连续的问题，访存的不连续必将带来额外的访存开销。解决这一问题可以根据循环的特点，对数据内存布局进行调整。

本文首先进行了循环交换优化，但交换之后访存的空间局部性不好，即相邻两次访存的地址不连续，存在较大跨度。这是因为快速PKTM算法中的模型空间与数据空间均以二维数组的形式存储，算法进行循环交换优化之后，访问二维数组的顺序与数组在内存中存放的顺序不一致，导致访存不连续。为解决这个问题，可以通过调整数据内存布局，将二维数组在内存中的存放顺序调整成算法循环过程中的访存顺序，以优化访存性能。数据内存布局调整前和调整后的访存模式如图6所示。

Figure 6 Memory access models before and after the exchange of loop variables

3.3 单一平台上的多线程并行

不论是传统CPU处理器还是新兴MIC平台均为多核或众核体系结构，充分挖掘应用程序的并发性、提高多个处理器核心的利用率是提高应用程序性能的关键要素之一。在这种具有共享存储特点的平台上，主要通过OpenMP多线程模型实现并行，为此需要对应用程序进行深入分析和并行性发掘。

3.3.1 任务分解的多线程并行

为了实现方便，最初采用分割最外层ib循环的方式进行任务分解，每个任务分别处理一段互不重合的ib范围，在整个模型空间及数据空间中进行遍历，发现满足有效性的点对(ix,is)和(ix±ib,it)，并完成相应的数据更新操作；多个任务并发处理，但由于不同任务中更新模型空间的位置有可能相同，为了避免线程级数据竞争，需要对模型空间点更新操作进行关键段保护(使用OpenMP的critical语句)或原子操作保护(使用OpenMP的atomic语句)。这种多线程并行在实现上只是针对循环书写编译指导语句，编程灵活、简单，并行效率高。

上述OpenMP多线程实现会出现数据竞争，导致某些线程空闲等待，造成线程资源的浪费以及时间的消耗。避免数据竞争需要保证线程之间访问的数据区域彼此不重合，需要对任务分解方案进行改进。

注意到PKTM算法的核心处理是对模型空间的nx×nt个离散网格点进行更新，由于各个离散网格点的更新过程相互独立、互不影响，因此，本质上可并发处理。因此可以针对模型空间的数据分割进行任务分解，为了在并发性和并行粒度两方面取得折衷，仅针对模型空间x-s平面中的s维进行一维分割，形成多个独立的并行任务。采用这种新的任务分解后，每个任务仅遍历模型空间的一个局部块，彼此之间互不重叠，不会发生同时写同一模型数据点的数据竞争；另一方面，尽管各任务间可能出现访问同一数据空间点的情况，但由于是读操作，不影响结果正确性，因此无需特殊处理。

在实现上，为了增大并行粒度，可简单地将代码中的ib循环与is循环进行交换，对最外层的is循环添加OpenMP编译指导语句。由于采用第3.2.2节访存优化技术，这种循环交换后不会引发访存性能问题。

3.3.2 多线程并行的运行配置与性能优化

为了充分提升多线程并行程序的运行性能，还要考虑应用程序跟操作系统、硬件平台间的协同问题，特别是任务调度及线程对处理器核的亲和性问题。

由于通常线程数目受处理器资源所限，通常要远小于并行任务的数量，采用何种策略将这些任务分配、调度到所有线程上，也会对性能造成直接影响，在下面的第3.4.2节专门详细讨论这个问题。

线程与处理器核绑定可以提高线程访问CPU的Cache命中率，从而提高程序的并行性能。

3.4 CPU+MIC异构平台上的混合并行

本文采用CPU为主MIC为辅模式，即offload模式进行CPU+MIC的混合并行。Offload模式适合串行计算程序中包含高并行计算部分，且并行部分并行度高的情况[9]。CPU+MIC混合并行的难点主要是任务分配和负载均衡的问题，混合并行的负载均衡涉及到不同计算能力的两个平台之间以及平台内部各线程之间的负载均衡。下面将分别介绍这两个层次的任务分配和负载均衡策略。

3.4.1CPU和MIC之间负载均衡

由于主频与核数的不同，CPU与MIC之间的处理能力有差异，为了达到不同平台之间的负载均衡，需要针对MIC和CPU的任务处理能力，对MIC和CPU的任务进行分配。本文用变量ratio表示上传到MIC上进行处理的任务占总任务的比例，通过调整ratio的值，可以得到最优的MIC与CPU任务数之比。当墙钟时间最短时，认为MIC与CPU的任务比达到最优，此时对应的ratio′( 1-ratio)的值即为最优的MIC与CPU的任务比。

3.4.2 CPU或MIC内部多线程之间负载均衡

(1)采用动态任务调度策略。

任务调度策略包括动态任务调度和静态任务调度。对于本应用，采用静态任务调度策略会导致负载不均衡，采用动态任务调度策略则可以缓解负载不均匀的情况。

理论上，PKTM算法求得的数据空间下标it的值与负载量之间满足以下关系：

(6)

其中，it为整数，且it∈[0,nt]。

公式(6)表明：对于确定的整数it，其负载量f(it)是可估算的，且负载量关于it递减，负载量f(it)的函数图像如图7所示(nx=8 000，nt=8 000，dt=0.004，dx=25，v=1 000时)。不妨假设线程数为2，采用静态任务调度策略时，任务将按照it递增的顺序交替分配给线程0和线程1，即所有it为偶数的计算任务交由线程0处理，所有it为奇数的计算任务交由线程1处理。假设分配给线程0和线程1的任务数相等，设为nTask，则线程0和线程1的负载量fp0和fp1可由公式(7)表示。

f(2)+…+f(2×nTask-2),

f(3)+…+f(2×nTask-1),

(7)

由于f(it)关于it递减，因此有f(0)>f(1),f(2)>f(3),…,f(nTask-2)>f(nTask-1)，于是fp0>fp1，导致线程0和线程1之间的负载不均衡，且这种不均衡性会随着任务数增加而更加明显。

采用动态任务调度策略会根据线程的实际任务完成情况来分配新任务，负载不均衡的现象可以得到一定缓解。Vtune的实测结果也反映了这一点，详见下一节内容。

Figure 7 Relationship between overload and variable it

(2)单个任务的粒度可调整。

为进一步解决负载不均衡问题，本文在采用动态任务调度的调度策略的同时，考虑利用chunksize变量调节任务的粒度。进行任务分配时的变量chunksize，其大小代表分配给线程的任务个数，chunksize的值越大，任务的粒度越大。本文将chunksize作为影响负载均衡问题的一个因素进行了一系列测试，通过调整chunksize值，测得一系列程序运行的墙钟时间，其中，最短的墙钟时间对应的chunksize值即为负载最均衡的chunksize值。

4 测试结果与分析

4.1 测试平台与环境

为考察第3节各类优化与效果，我们使用一个单结点的CPU+MIC异构计算机系统进行了测试。测试平台的环境与参数如表1所示。

Table 1 Test platform and circumstance

4.2 典型优化方法的效果

第3节提到的各种优化方法相互之间有一定影响，所以单独表示各个方法的性能比较困难。本文主要将之前提到的典型优化方法融入到了3个主要版本中，测得问题规模为nt=8 000，nx=8 000时，几个典型优化方法的性能提升如图8所示。

Figure 8 Performance improvement of classical optimization methods

图8中，横坐标为版本号，版本1(包括v1.0，v1.1和v1.2)均为基于经典PKTM算法的优化版本，版本2(包括v2.0和v2.1)基于快速PKTM算法，版本3(包括v3.0和v3.1)为CPU+MIC协同异构平台下的优化版本。版本1主要进行的优化包括编译器优化，Pthread改为OpenMP和提前确定迭代次数；版本2主要进行的优化包括常量计算提前、循环交换、调整数组顺序，利用对称性减少迭代次数，线程动态任务分配；版本3主要是在版本2的基础上进行MIC移植，改进了CPU与MIC之间的负载比例。

图8的纵坐标代表获得的性能提升，CPU的最优性能在16线程的条件下获得，性能提升的基准为经典PKTM并行算法的CPU性能；MIC的native模式最优性能在180线程的条件下获得，性能提升的基准为基于经典PKTM并行算法的MIC native模式性能；CPU+MIC的offload模式最优性能在CPU端16线程、MIC端240线程×单MIC卡的条件下获得，性能提升的基准为经典PKTM并行算法的CPU性能。具体性能提升如表2所示，最优时间1.66 s与最原始的经典PKTM并行算法的357.52 s相比，性能提升了214.37倍。

Table 2 Performance improvement

4.3 问题规模取值对计算量的影响

问题规模对程序的计算量有一定影响，从而影响到优化的性能。比如在快速PKTM算法中提前确定迭代次数的优化方法，在固定规模nx=8 000，nt=8 000的条件下,it的计算量减少了约84%，对应不同规模的组合，减少的计算量也不同。

本文针对基于快速PKTM算法的提前确定迭代次数的优化，测试了几组不同规模对算法计算量以及性能提升的影响。测试结果如图9所示。

Figure 9 Effect of scale combination on the amount of computation

图9四幅图的横坐标代表ix的取值范围，纵坐标是最大计算量比，表示对应一个具体ix，实际产生有效it时的计算量占优化前计算it需要的计算量的比例。如图9d中,ix=319时，最大计算量比为0.13，表示优化前求it所进行的计算中，只有13%的计算产生了有效的it，而87%的计算量不满足条件判断。经过提前确定迭代次数的优化，可以有效剔除无效计算，性能优化的效果与问题规模的组合有关。如nx=2 000，nt=1 000时(如图9d所示)，最大计算量比为0.13，在此组合下进行提前确定迭代次数的优化至少能减少87%的计算量；而nx=1 000，nt=4 000时(如图9c所示)，最大计算量比为0.9，优化后能减少的计算量为10%，不如图9d的效果好。

4.4 典型优化方法效果展示

固定问题规模nx=8 000，nt=8 000之后，仍然有一些因素会对优化性能造成一定影响，如3.4节提到的，将程序移植到MIC平台上与CPU协同处理的过程中涉及到的负载平衡问题，任务调度策略会影响性能，同时线程任务粒度的大小对性能也有一定影响。

4.4.1 CPU或MIC内部多线程之间的负载均衡

之前介绍了CPU与MIC之间的处理能力有差异，因此需要针对MIC和CPU的任务处理能力，对MIC和CPU进行任务分配。图10显示了调整MIC与CPU任务分配比例对程序运行性能的影响。其中横坐标为变量ratio(单位为0.1)，它表示分配到MIC端的任务数占总任务的比例，纵坐标代表按照ratio划分任务后程序执行的墙钟时间。从图10可以看出，当ratio约为0.5时，墙钟时间最短，此时可以认为MIC与CPU之间的负载大致平衡，对应的MIC与CPU之间最优任务数之比约为1∶1。

Figure 10 Allocation performance of load balance between MIC and CPU

4.4.2 动静态任务调度策略

3.4.2节已从理论上分析了动态调度相较于静态调度负载更为平衡，Vtune实测的结果也表明动态任务调度负载的优势。图11是利用Vtune实测出的程序在不同任务调度策略下的运行情况。图11a采用静态任务调度策略，其中第五个线程是瓶颈，其结束时间最晚，且与其它线程的结束时间相差较大，程序实际运行时，其它运行结束的线程都在等待第五个线程结束，造成严重的资源浪费。图11b采用动态任务调度策略，所有线程的结束时间相差很小，没有线程空等的现象，资源利用率高，且与静态任务调度策略相比，动态任务调度的墙钟时间更短。

Figure 11 Load balance of static and dynamic scheduling

4.4.3 线程任务粒度大小

本文在考虑调度策略对性能造成影响的同时，也考虑了线程任务粒度(chunksize)对负载均衡造成的影响。进行任务分配时的变量chunksize，其大小代表分配给线程的任务个数，chunksize的值越大，任务的粒度越大。不同的任务粒度会影响程序的负载情况，经过实测得到chunksize与墙钟时间的关系如图12所示，其中横坐标代表不同的chunksize的大小，纵坐标代表对应的程序运行墙钟时间。由此可知，采取静态任务调度，chunksize=6时墙钟时间最短，负载相对平衡；采取动态任务调度策略，chunksize=5时墙钟时间最短，负载相对平衡。

Figure 12 Effect of chunk size on load balance

5 测试结果与分析

本文针对Kirchhoff叠前时间偏移算法处理地震勘探数据的问题，基于CPU+MIC协同异构平台，采用提前确定迭代次数、常量计算提前、循环交换、数据内存布局调整、利用对称性减少迭代次数、线程动态任务分配、改进CPU+MIC负载比例等一系列方法对原始程序进行移植和优化，对于6 000万规模(8 000×8 000)的应用问题，总的并行模拟时间从357.52 s减少到1.66 s，性能提升了214.37倍。本文第4节的应用问题来源于中国计算机学会高性能计算专业委员会与Intel公司联合举办的2013年全国教育科研并行应用程序优化大赛决赛题目，作者所在团队以本文优化方法及效果获得最高异构计算性能奖。

本文针对异构平台计算能力的差异，进行了一系列的分析与测试，总结出影响异构平台负载平衡的几方面因素，并通过Vtune等进行了验证，最终确定负载平衡的策略。本文进行的优化和分析策略可以扩展到其它相似的异构程序移植中去。

后续工作主要可以从两方面入手，一是可以进一步分析并行程序的可扩展性，二是针对更大的问题规模，可以考虑使用MPI多进程将程序扩展到多个结点上并行。

[1] Zhao Chang-hai, Wang Shi-hu, Luo Guo-an, et al. A highly extensible 3D prestack kirchhoff time migration parallel algorithm[C]∥National Annual Conference on High Performance Computing, 2013:49-60.(in Chinese)

[2] Jeffers J, Reinders J. Intel® Xeon Phitmcoprocessor high-performance programming[M]. NY:Elsevier, 2013.

[3] top500 supercomputer sites[EB/OL].[2014-10-16].http://www.top500.org.

[4] Bhardwaj D, Yerneni S. Efficient parallel I/O for seismic imaging in a distributed computing environment[C]∥Proc of

the 3rd Conference and Exposition on Petroleum Geophysics, 2000:105-108.

[5] Wang Hua-zhong, Liu Shao-yong, Kong Xiang-ning, et al. 3D Kirchoff PSDM for large-scale seismic data and its parallel implementation strategy[J]. Oil Geophysical Prospecting, 2012, 47(3):404-410.(in Chinese)

[6] Zhang Qing, Chi Xu-guang, Xie Hai-bo,et al. Parallel algorithm based on the travel time computing of pre-stack time migration using GPU[J]. Computing Systems & Applications, 2011,20(8):42-46.(in Chinese)

[7] Claerbout J F, Green I. Basic earth imagine[M]. California:Stanford University, 2008.

[8] Claerbout J F. Introduction to Kirchhoff migration programs[R]. California:Stanford Exploration Report, 1997:385-391.

[9] Wang En-dong, Zhang Qing, Shen Bo, et al. MIC High performance computing programming guide[M]. Beijing:China Water & Power Press, 2012.(in Chinese)

附中文参考文献：

[1] 赵长海, 王狮虎, 罗国安，等. 一个高度可扩展的三维叠前Kirchhoff时间偏移并行算法[C]∥全国高性能计算学术年会, 2013:49-60.

[5] 王华忠, 刘少勇, 孔祥宁, 等. 大规模三维地震数据Kirchhoff叠前深度偏移及其并行实现[J]. 石油地球物理勘探, 2012, 47(3):404-410.

[6] 张清, 迟旭光, 谢海波，等. 基于GPU实现叠前时间偏移走时计算的并行算法[J]. 计算机系统应用, 2011, 20(8):42-46.

[9] 王恩东, 张清, 沈铂，等. MIC高性能计算编程指南[M]. 北京:中国水利水电出版社, 2012.

XIONG Min,born in 1990,PhD candidate,CCF member(E200036553G)，her research interests include large scale engineering and science computation.

王勇献(1975-),男,河南安阳人，博士，副研究员,CCF会员(E200021304M),研究方向为高性能计算。E-mail:yxwang@nudt.edu.cn

WANG Yong-xian,born in 1975,PhD,associate research fellow,CCF member(E200021304M),his research interest includes high performance computing.

Parallel optimization of the seismic wave PKTM algorithm on CPU+MIC heterogeneous platform

XIONG Min，WANG Yong-xian

(College of Computer,National University of Defense Technology,Changsha 410073,China)

An efficient technique which is now being implemented in photographing images of complicated rock stratum is the seismic wave PKTM algorithm. With the earthquake prediction coming into massive data generation, it is of essential importance to optimize this algorithm by parallel computation. In recent years, high performance parallel computation is characterized by heterogeneous and many cores systems.A typical example of this kind of processors, featured with low cost and high performance is Xeon Phi, being known as MIC. On the basis of the classic PKTM algorithm, we parallelize and optimize the PKTM algorithm in the offload programming model, based on CPU+MIC heterogeneous platform. For applications with the scale of 64 000 000(8 000×8 000),the total parallel simulation time is reduced from 357.52 seconds to 1.66 seconds, achieving 214.37x performance improvement.

collaborative parallel;Intel Xeon Phi;heterogeneous parallel;Kirchhoff Time Migration；performance optimization

1007-130X(2015)01-0014-09

2014-09-10;

2014-11-12基金项目：空气动力学国家重点实验室开放课题资助项目(SKLA201401)；国家自然科学基金资助项目(61379056, 11272352)

TP274

A

10.3969/j.issn.1007-130X.2015.01.003

熊敏(1990-),女，湖南长沙人，博士生，CCF会员(E200036553G)，研究方向为大规模工程与科学计算。E-mail:miyazawa21yy@aliyun.com

通信地址：410073 湖南省长沙市国防科学技术大学计算机学院学员五队

Address:College of Computer,National University of Defense Technology,Changsha 410073,Hunan,P.R.China