基于随机子空间识别的模态参数不确定性量化方法

罗 杰, 康 杰, 孙嘉宝, 曾舒洪

(南京航空航天大学 航天学院,南京 211106)

模态参数识别是结构健康监测中常用的技术,通过分析结构的振动响应信号,识别出结构的特征参数,如频率、阻尼、模态振型等[1-3]。协方差驱动随机子空间识别(covariance-driven stochastic subspace identification,SSI-COV)方法作为模态参数识别方法的一种,利用其强鲁棒性、高精度等优势,被广泛应用于仅有输出响应数据的工作模态分析中,用于提取结构的模态频率、阻尼比和模态振型[4-5]。SSI-COV的计算模态参数过程可分为以下几个步骤:首先,收集传感器信号,将每一时刻的响应按列排列,估计相关函数矩阵,并组成Hankel矩阵的形式;然后对Hankel矩阵进行奇异值分解(singular value decomposition,SVD)运算,根据分解的结果计算出状态矩阵O,从而获得系统矩阵A和输出矩阵C;最后,对系统矩阵A进行特征值分解运算,并将分解的特征值、特征向量转化成连续时间系统状态矩阵的特征值和特征向量,根据连续系统的特征值和特征向量获得结构的模态频率、振型和阻尼比等结构模态参数。

由于振动测量噪声、数据长度有限等因素的存在,SSI-COV方法在实际应用中,模态参数识别结果会受到不确定性的影响,因此需要对模态参数的不确定度进行量化[6]。获得的不确定度可用于评估模态参数估计结果的质量,并能够剔除虚假模态;还用于考虑结构动力学参数不确定性的结构设计、模型修正等问题的研究[7-8]。Reynders等[9-10]利用矩阵一阶扰动分析方法量化了SSI-COV方法识别模态参数的不确定度,并给出了具体的公式推导过程。Carden等[11]利用SSI估计了大型民用基础设施模态参数的置信区间。这些方法在计算各中间变量的扰动时,均采用矩阵拉直以及Kronecker积等数学运算来推导出模态参数的方差。这种计算方法会导致矩阵维度高、运算效率低等问题。

针对该问题,本文提出了一种基于SSI-COV的模态参数不确定度高效计算方法。首先,计算振动响应相关函数的方差,通过SVD,选取恰当的奇异值截断阶数,由每阶奇异向量组装,获得多组Hankel矩阵的扰动。其次,根据一阶矩阵摄动理论,隐式计算SSI-COV算法中各中间变量的一阶扰动,最终,由多组模态参数的扰动叠加计算出方差。

本文组织结构如下:第1节概述SSI-COV方法原理和计算过程;第2节介绍本文提出的不确定度高效计算方法,并与已有方法相比,讨论了计算量的不同;第3节利用桁架结构数据对提出的方法进行蒙特卡洛仿真(Monte Carlo simulation,MCS)验证,并对上一节的计算量对比分析具体化,第4节对本文进行总结。

1 SSI-COV方法原理

1.1 离散时间状态空间模型

具有N个自由度系统,在外界环境激励下的运动微分方程可以表示为

(1)

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;q(t)为t时刻的位移列向量;f(t)为外部激励向量。

在实际测试中,考虑到信号采集的时间离散性和测量时存在的噪声干扰现象,对式(1)进行采样离散化处理和微分求解,得到的系统离散时间状态空间模型为[12]

(2)

式中:yk和xk分别为第k个采样时刻系统的输出向量和状态向量;wk和vk分别为环境干扰噪声序列和传感器自身测量误差所带来的噪声序列;A为系统状态矩阵;C为系统输出矩阵。

此空间模型是由状态方程和输出方程组合,构成一个系统完整的动态描述。其基本假设前提为

(1)噪声项为均值为零的平稳随机过程,即

E[wk]=0, E[vk]=0

(3)

(2) 噪声信号是均值为零的白噪声序列,且与结构真实状态无关,即

(4)

(3) 系统为线性时不变系统(既满足叠加原理又 具有时不变特性),状态序列为平稳随机过程,即

(5)

式中: E为数学期望;Σ为状态协方差矩阵;k为时间。

1.2 模态参数识别

根据系统的输出响应求出相关函数矩阵,在实际测试中,通常只选取一段数据量参与计算,因此,输出协方差矩阵可估计为[13]

(6)

式中:yk∈m×1;τ为相关函数时延;S为数据点个数;k为第k个时刻且k=1,2,3,…,S;m为输出通道数。

根据式(6)相关函数构造Hankel矩阵为

(7)

式中,i和j分别为Hankel矩阵的列块数和行块数。对Hankel矩阵进行SVD,得

(8)

式中:U为左奇异矩阵;Σ为奇异值矩阵;V为右奇异矩阵。

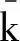
(9)

则系统矩阵A和输出矩阵C可分别表示为

(10)

式中:O1:m为可观矩阵O的前m行形成的新矩阵;O↑为去掉矩阵O后m行形成的新矩阵;O↓为去掉矩阵O前m行形成的新矩阵。

由矩阵A特征值分解得

(11)

式中:λ为特征值;ψ为右特征向量;β为左特征向量;H为取复共轭转置。

则第d阶结构模态频率fd、阻尼比ξd和模态振型φd可分别表示为

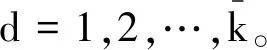
1.3 Hankel矩阵维度及模型阶数确定

在对结构进行模态辨识之前,需要选取一系列模型参数。其中Hankel矩阵维度和模型阶数的选择对随机子空间法的辨识结果影响十分显著,因此针对不同的系统结构,选择不同的参数具有重要意义[15]。Hankel矩阵维度可根据下列公式确定

j+i-1≤S

(13)

(14)

(15)

式中,fs和f0分别为采样频率和基频。

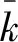
2 模态参数不确定度量化

由于辨识的模态参数总是受到许多不同来源的统计不确定度的影响,如响应测量噪声与数据有限长度,因此,需要对已辨识的模态参数进行不确定度量化。最开始计算不确定度的方法需显式表示出Jacobian矩阵,导致矩阵运算维度高、计算效率低。文献[9]提出了一种无需显式计算Jacobian矩阵的方法,本文采用该方法进行模态参数的不确定度量化,基于一阶矩阵摄动理论逐级计算误差扰动,估计模态参数的方差。

2.1 Hankel矩阵的扰动估计

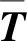
(16)

式中,vec(·)为矩阵拉直运算。对cov(T)进行SVD,则cov(T)可近似为

(17)

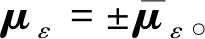
(18)

由矩阵T得到的扰动矩阵与矩阵T大小保持一致,所以将扰动向量转换成jm×im矩阵,即为矩阵T的第ε阶扰动,记作ΔTε,其中ε=1,2,3,…,n。

由于式(16)中Hankel矩阵T的方差矩阵维度为ijm2×ijm2,维度高,对计算机内存的需求较大。观察可知,Hankel矩阵T中存在很多重复的相关函数矩阵块,利用该特点可以大幅度降低计算量。

提取其中一个相关函数矩阵块,记为

(19)

(20)

对方差矩阵cov(R)进行SVD,文献[16]需要进行nb次运算,为了进一步降低计算量,可选择奇异值阶数q进行截断,得到R矩阵的q阶扰动为

(21)

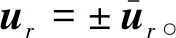
(22)

将扰动向量Δδr重组成大小为m×(i+j-1)m的矩阵,再按式(7)中排列顺序填入对应的位置,即可获得Hankel矩阵T的第r阶扰动矩阵,记作ΔTr,其中r=1,2,…,q。

上述方法避免了直接计算Hankel矩阵的方差矩阵cov(T),并且进行奇异值截断,降低计算量的同时大幅节省了存储方差矩阵的内存空间。

2.2 模态参数的方差估计

首先,根据一阶矩阵扰动传播理论,由式(8)可知,Hankel矩阵将扰动传递给奇异值和奇异向量。

(23)

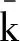
(24)

考虑T矩阵存在扰动ΔT,由式(24)可得

ΔTvc+TΔvc=Δσcuc+σcΔuc

(25)

(26)

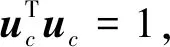
(27)

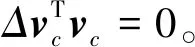
(28)

将式(24)左右奇异向量分离变量,考虑矩阵T存在扰动ΔT,可得

(29)

将式(24)、式(28)代入式(29),得

(30)

式中:I为单位矩阵;T为矩阵转置。

针对式(17)得到的每阶扰动,均可计算出矩阵T奇异值、奇异向量的对应扰动。由矩阵T第r阶扰动引起的第l阶奇异值、奇异向量的扰动为

(31)

则由矩阵T第r阶扰动引起的奇异值、奇异向量矩阵的扰动可记为

(32)

考虑O矩阵存在扰动,由式(9)可得状态矩阵O的扰动为[15]

(33)

考虑输出矩阵C、系统矩阵A存在扰动,由式(10)可得[15]

ΔCr=S3ΔOr

(34)

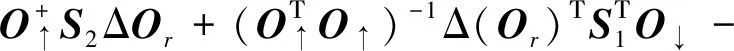
(35)

式中:

S1=[I(j-1)m×(j-1)m0(j-1)m×m]

S2=[0(j-1)m×mI(j-1)m×(j-1)m]

S3=[Im×m0m×(j-1)m]

考虑特征值、特征向量存在扰动,由式(11)可得

(36)

(37)

根据文献[9],由第r阶特征值扰动引起的第d阶模态频率、阻尼的扰动为

(38)

式中:μd=ln(λd)/Δt;Im(·)为取复数的虚部。

同理,由第r阶特征向量的扰动引起的第d个模态振型的扰动为[9]

Δφd,r=ΔCrαd+CΔαd,r

(39)

但是,通常结构模态振型为复数形式,需要进行归一化处理。归一化选择对模态振型上的每一个点除以任意选择的点φd,w进行归一化,则模态振型的扰动则进一步转化为[9]

(40)

式中,S4∈1×m为在w处为1其他处均为0的行向量。

根据式(38)、式(40)可得由第r阶矩阵T的扰动引起的第d阶频率、阻尼、模态振型的方差为

(41)

借助于式(41)计算出的模态参数方差,式(21)中的扰动截断阶数q可根据如下准则确定

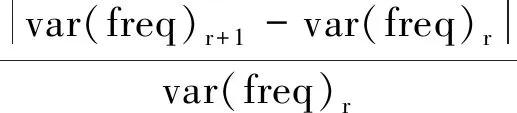
(42)

式中,r为截断阶数。满足该准则的最小r值即为最终确定的扰动截断阶数q。

在已有方法文献[14]中,通常计算T矩阵的扰动,先将数据响应分段分别计算矩阵T,利用每一段矩阵T和所有矩阵T的均值相减直接获得其扰动。而在第2.1节和本节的方法中,先计算相关函数的方差矩阵,进行SVD,并选择适当的奇异值截断阶数,可有效降低扰动矩阵计算的次数,最后由奇异值、奇异向量计算出的扰动矩阵来组装T矩阵的扰动。因此,本文在计算T矩阵的扰动以及最终模态参数的扰动时更加高效。另外,在文献[16]中,扰动传播表达式的推导均利用Kronecker积和矩阵拉直运算,将扰动写在方程最右侧,例如式(43)写为

Δσc=(vc⊗uc)Tvec(ΔT)

(43)

由于上式中包含Kronecker积和矩阵拉直运算,vc⊗uc的维度为1×ijm2,需要ijm2次乘法计算,Δσc总的计算量包含2ijm2次乘法和(ijm2-1)次加法;而式(28)中矩阵维度更小,总的计算量为ijm2+jm乘法和(ijm2-1)次加法,计算量更小。

3 桁架结构仿真算例验证

本节采用文献[17]中的桁架结构模型验证所提方法的有效性。桁架结构模型如图1所示,弹性模量为6.98×1010Pa,材料密度为2 770 kg/m3,并在节点①、节点②、节点③、节点④上加入454 kg的额外集中质量,Ai为第i根杆件横截面积,其阻尼矩阵与质量矩阵成正比且第一模态阻尼等于1%,表1和表2给出了桁架结构真实模态频率和阻尼比。

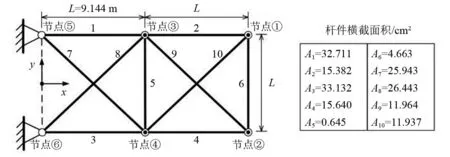
图1 桁架结构图Fig.1 Truss structure

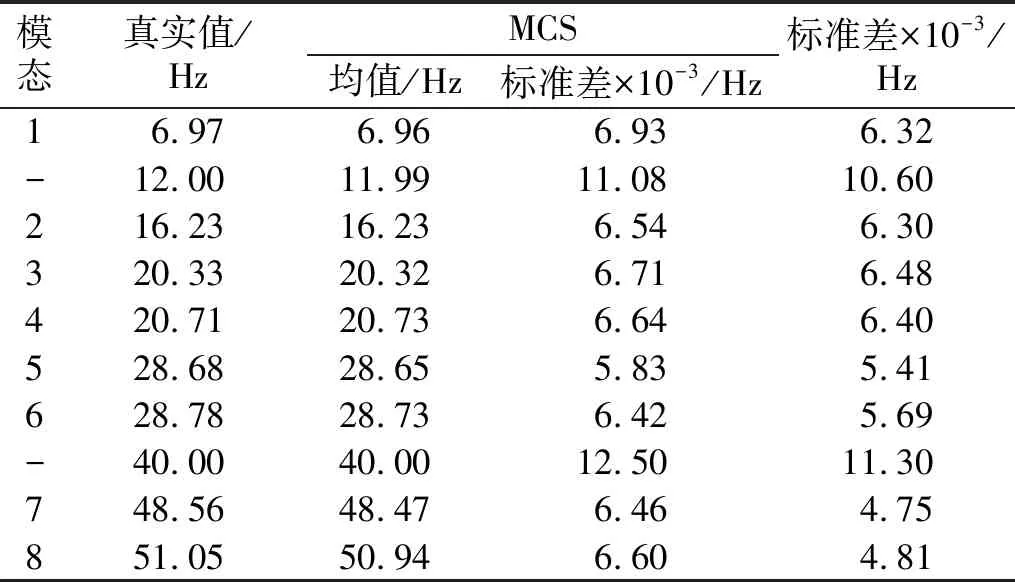
表1 模态频率估计值的标准差Tab.1 Standard deviation of frequency estimates

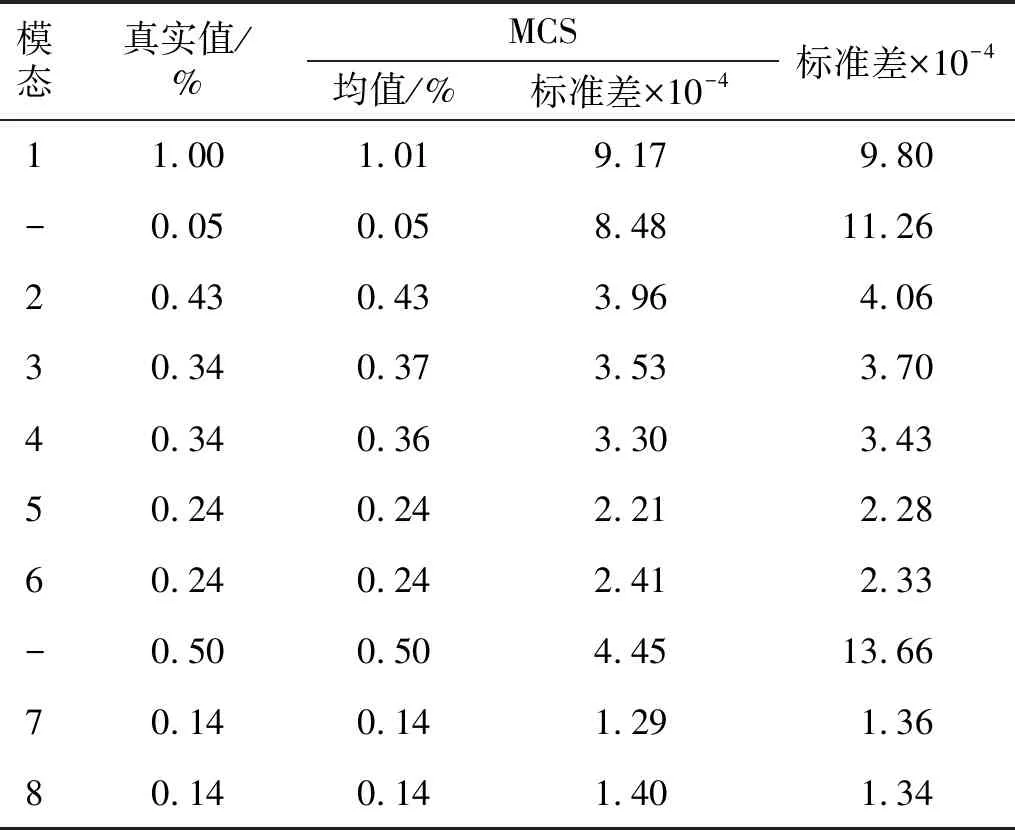
表2 模态阻尼比估计值的标准差Tab.2 Standard deviation of damping estimates

本算例中采用三种类型的激励(即白噪声、谐波激励和非白噪声激励),其中谐波激励的频率为12 Hz;非白噪声激励由白噪声经过单自由度系统过滤得到,滤波函数为:

(44)

式中,s为Laplace变换算子,单自由度系统的阻尼比ζ0=0.5%,固有频率ω0=40 Hz。

本文在节点①的x、y方向同时作用谐波激励与非白噪声激励,且沿节点①的x、y方向的激励完全相关,节点②、节点③、节点④的x、y方向同时作用不相关高斯白噪声激励。使用Newmark-β方法计算桁架结构的位移响应,响应信号所加信噪比为20 dB,时间步长为1/1 024 s,总时长320 s;随后进行128 Hz重采样,因此位移响应数据点数为40 960。

3.1 仿真结果

利用SSI-COV方法估计桁架结构模态参数,并根据本文所提方法计算模态参数标准差。将得到的模态参数标准差与MCS方法得到的模态参数标准差进行比较,从而验证本文方法的有效性和可行性。

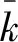
图2 Hankel矩阵奇异值变化曲线Fig.2 Singular value curve of Hankel matrix

对于相关函数方差矩阵奇异值截断阶数q的选取,本文提取了第4个模态的频率方差进行计算,其截断阶数为20时对应的频率方差为4.699 66×10-05,截断阶数为21时对应的频率方差为4.707 37×10-05,经式(42)计算,当r=20时的截断系数为0.001 6,同理,当r=18时计算出的截断系数为0.12,r=22时计算出的截断系数为0.000 7,故确定出有效截断阶数q为20。如图3所示,显示的四条曲线表示系统前四阶模态频率的方差,横轴表示相关函数方差矩阵进行SVD所截断的阶数,纵轴表示估计的模态频率方差。不难发现,随着截断阶数的增加,约20阶以后,估计的模态频率方差开始趋于稳定。所以,本文选择q=20作为相关函数方差矩阵的截断阶数,不仅能确保模态参数不发生较大偏差,还降低了同原来方法一半的计算量,大幅提高了原有算法的计算效率。

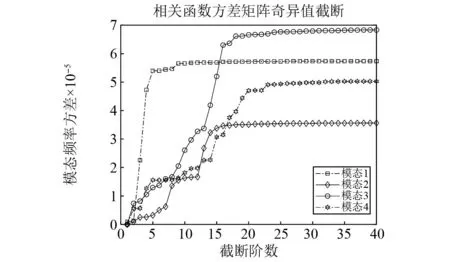
图3 奇异值截断阶数对模态频率方差的影响Fig.3 The effect of singular value truncation order on modal frequency variance

确定固定参数后,进行500次MCS,通过SSI-COV方法估计桁架模态参数。估计的第一阶模态频率、阻尼比如图4和图5所示。结果显示,所有离散的样本点都在数值1上下波动,辨识值与真实值接近,并未出现异常的辨识结果,说明仿真结果是可靠的。

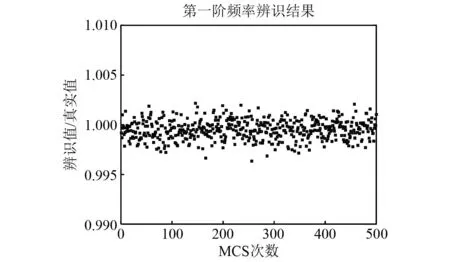
图4 第一阶模态频率辨识结果Fig.4 First-order modal frequency identification results

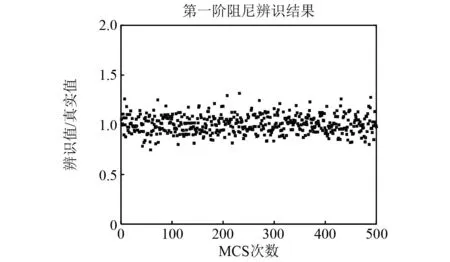
图5 第一阶模态阻尼辨识结果Fig.5 First-order modal damping identification results

其次,将所提方法计算的模态参数标准差与MCS得到的样本统计量进行比较。在每次仿真中,通过第2.2节中提出的方法估计模态频率、阻尼比和模态振型的标准差,随后计算500次估计标准差的均值。将此标准差均值与500次MCS得到的样本标准差进行比较,模态频率和阻尼比结果如表1和表2所示,模态振型对比结果如图6所示。

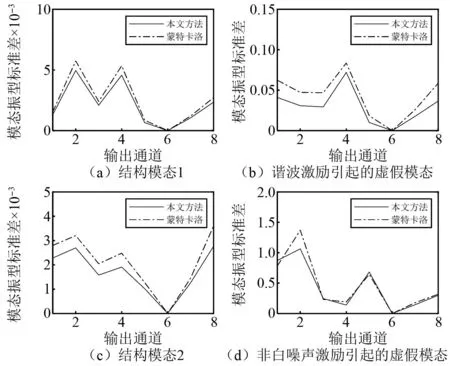
图6 模态振型标准差Fig.6 Standard deviation of modal shape

结果显示,SSI-COV方法能够完整地估计8阶结构模态,识别结果中频率为12 Hz与40 Hz的两阶模态是由谐波激励和有色噪声激励引起的,属于虚假模态。由此发现,SSI-COV方法在模态参数识别过程中无法剔除虚假模态。但是,由计算获得的模态参数不确定度结果表明,对于由非白噪声激励或谐波激励引起的已识别的虚假模态,其频率和阻尼比的不确定度显著大于结构模态的不确定度,可以利用该特性来完成对虚假模态的剔除。且所提方法计算的模态参数标准差总体小于MCS中模态参数样本计算的标准差。

对于模态振型的标准差,选择了第1、第2阶的结构模态振型不确定度和虚假模态(谐波激励、非白噪声激励)的模态振型不确定度结果进行比较。如图6所示,实线表示由本文方法计算的不确定度结果,虚线则由MCS模态参数样本计算的不确定度结果。通过观察,由本文方法计算的模态振型的不确定度同样比仿真结果偏大,且虚假模态计算的振型标准差显著大于结构模态的振型标准差,由振型标准差的结果,可进一步作为判断虚假模态的依据。

下面通过讨论不同Hankel维度对所辨识的模态参数不确定度的影响。文中讨论了Hankel矩阵行分块数为30、60、90等三种不同情况对辨识出的模态参数不确定度的影响,除矩阵行块数j以外其余的固定参数设置保持不变。

模态频率、阻尼的不确定度如图7和图8所示,观察可知,随着Hankel矩阵维度的变化,由谐波激励产生的模态频率、阻尼的不确定度变化幅度较大且没有规律,该特点也可作为判断虚假模态依据。由非白噪声产生的模态频率不确定度总体上与结构真实模态频率的不确定度变化一致,随着Hankel矩阵维度增加而增大,但非白噪声激励引起的模态频率对应的不确定度显著大于结构模态频率的不确定度。而对于阻尼模态频率的不确定度来说,结构模态的不确定度随Hankel矩阵维度变化很小,虚假模态的不确定度变化较为明显。

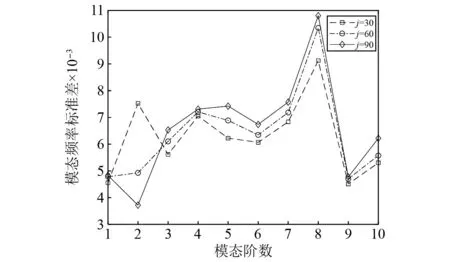
图7 不同Hankel矩阵维度对模态频率不确定度的影响Fig.7 Influence of different Hankel matrix dimensions on modal frequency uncertainty

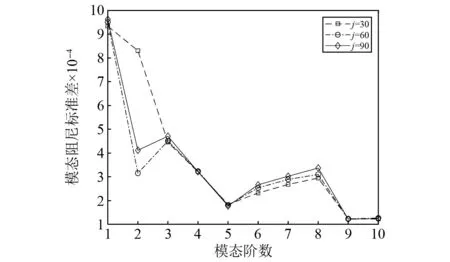
图8 不同Hankel矩阵维度对模态阻尼不确定度的影响Fig.8 Influence of different Hankel matrix dimensions on modal damping uncertainty

3.2 不确定度量化的计算量分析

下面就本文方法和传统方法的计算量作具体对比,分析在实际计算过程中,两者计算量上存在的差距,从而验证本文所提方法的有效性。以下讨论的固定参数同仿真分析数值一致。

传统方法中,例如文献[12]的方法,计算T矩阵扰动,先将数据响应分段分别计算矩阵T,利用每一段的矩阵T和所有矩阵T的均值相减直接获得其扰动。根据响应数据分段次数为40,所以还需计算40次T的扰动,整个模态参数的扰动计算也随之计算40次。在文献[11]中计算各中间变量的不确定度时,如式(43)计算奇异值的扰动,vc⊗uc的维度为1×38 400,需要38 400次乘法计算,Δσc总的计算量包含76 800次乘法和38 399次加法。

在本文所提方法中,利用式(19)、式(20)先求相关函数矩阵块R的方差,进行SVD,根据截断准则在截断阶数为20时进行截断。而已有文献[15]中数据分段数nb为40,所以扰动T原本需要40次运算现缩减至20次。同理,各中间变量的扰动计算次数也随之减少一半,整个模态参数不确定度计算效率提高50%。另外,绕过矩阵拉直以及Kronecker积等数学运算,利用式(28)中计算Δσc,总的计算量为38 640次乘法和38 399次加法,与上述过程相比,减少了一半的乘法,提高了计算效率。同理,在计算各中间变量的每一阶扰动时,本文所提方法跟传统方法相比,均减小了一定的计算量。

所以,在整个模态参数不确定度计算过程中,本文提出的方法大幅地提高了原有算法的计算效率、降低了对内存的需求。

4 结 论

本文提出了一种基于SSI-COV模态参数不确定度高效计算方法,通过相关函数矩阵的方差进行SVD,根据奇异值截断阶数准则,选择合适的截断阶数q,可显著降低计算量,然后由各阶扰动向量组装成q组Hankel矩阵的扰动。根据一阶矩阵扰动传播理论和SSI算法,绕过传统的Kronecker积和矩阵拉直等数学运算,逐级计算各中间变量的扰动,从而获得多组模态参数的扰动,通过扰动平方求和计算模态参数的方差。

最后应用本文方法对桁架结构算例仿真,通过比较结构模态和虚假模态的方差,证明了不确定度计算可用来剔除模态参数识别中的虚假模态。与已有方法比较,本文所提方法能够大幅地提高了计算效率、降低了对内存的需求。