考虑泄漏和温度效应的黏滞阻尼器性能演变研究

杨孟刚, 曹恺悦, 李 新, 胡尚韬

(1.中南大学 土木工程学院,长沙 410075;2. 中船双瑞(洛阳)特种装备股份有限公司,河南 洛阳 471000)

桥梁和建筑结构在地震、风和车辆等外荷载作用下会产生振动,严重时甚至可能引起桥梁和建筑的垮塌,因此对结构的振动进行控制是十分必要的。自20世纪90年代中期起,一系列耗能减振装置被迅速地推广运用开来[1]。其中被动控制是一种无需外部供能即可为结构提供控制力的振控装置[2]。速度型黏滞流体阻尼器便是一种经典的被动耗能装置,由于具有理念清晰、构造简单、阻尼特性易于控制等优点,在土木工程结构中被广泛使用[3]。

然而,黏滞阻尼器在服役周期内会不可避免地存在力学性能演变的问题,其中阻尼液的泄漏是一个十分重要的原因。目前,已有许多安装了黏滞阻尼器的实际工程出现了漏油现象[4],例如美国的南加州大桥、文森特托马斯大桥、杭州东大桥和北京阜成门桥等[5]。陈永祁[6]提出,影响漏油的关键因素有高压密封容器、密封装置、内部零件加工精度等。Wang等[7]发现,液压阻尼器中夹带的空气和安装间隙会使得液压阻尼器的缓冲效果减弱。与之类似,Yan等[8]对一种新型自复位黏滞阻尼器进行了试验研究,认为在低频加载的卸载阶段,阻尼器滞回曲线的不规则是由于硅油未充满缸体造成的。苏何先等[9]在参与黏滞阻尼器性能测试等相关试验时,发现了油液泄漏、活塞杆屈曲和缸体破坏等产品质量问题。Francesco等[10-11]以洛杉矶的Vincent Thomas桥作为研究对象,对性能演变黏滞阻尼器的桥梁地震反应进行了修正。杨孟刚等[12-13]设计了一种黏滞-软钢阻尼器组合系统,该组合系统能在一定程度下提高其耐久度,但仍未解决黏滞阻尼器的漏油问题。

除阻尼器油液泄漏之外,温度变化对黏滞阻尼器力学性能的影响也是不可忽视的。陈倩等[14]对黏滞阻尼器进行了试验,结果发现黏滞阻尼液的热力学性能对阻尼器的稳定性有重要影响。普静狄[15]对比了各国规范中温度相关性能测试的方法和要求,说明温度相关性是评价阻尼器性能的一项必要指标。Kim等[16]针对控制推进轴系统扭转振动的高黏度黏滞阻尼器,提出了考虑工作温度和老化的系统优化设计。Esfandiyari等[17]提出温度的升高可能会导致黏滞阻尼器的密封件的老化和损坏。Lak等[18]对黏滞阻尼器开展了短期和长期加载下阻尼器自身发热的相关试验研究,并提出了一种预测阻尼器各部件温度的数值模拟方法。Guo等[19]建立了一个预测风和地震响应下黏弹性阻尼器的热力学响应模型,以模拟动力荷载作用下温度和频率相关的阻尼性能。

已有文献表明,漏油和温度效应是影响黏滞阻尼器性能的最重要的两个因素,且实际工程中,油液泄漏和温度作用往往同时存在。然而,目前研究多针对漏油和温度的单一影响,还未有学者考虑黏滞阻尼器在二者联合作用下的性能演变模式,因此,本文从黏滞阻尼器漏油程度和环境温度两个方面出发,通过有限元仿真和滞回试验的方法,对比探究了两种因素单独和联合作用下黏滞阻尼器力学性能的变化规律,建立并验证了黏滞阻尼器的性能演变力学模型。

1 黏滞阻尼器性能演变试验与分析

1.1 试验分析用的黏滞阻尼器

液体黏滞阻尼器是一种内设活塞的筒状装置,一般由活塞杆、油缸、密封件和油腔内的黏滞流体硅油组成,其最常用的力学模型为

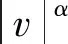
(1)

式中:F为阻尼力;C为阻尼系数;α为速度指数;v为活塞与缸体的相对运动速度; sgn(v)为符号函数,仅表示方向。

本研究采用的阻尼器为洛阳双瑞特种设备有限公司生产的FVD1500-e300-00黏滞阻尼器,其基本构造如图1所示,各项基本设计参数和结构尺寸如表1所示。

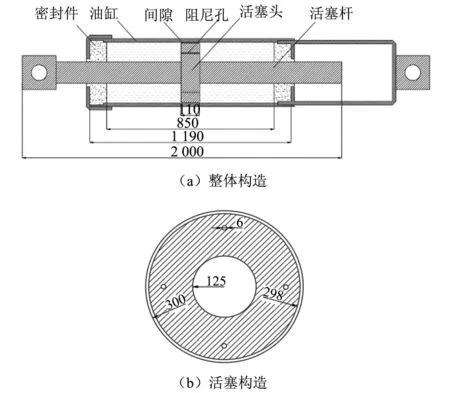
图1 FVD1500-e300-00黏滞阻尼器构造(mm)Fig.1 The configuration of FVD1500-e300-00

1.2 黏滞阻尼器的漏油性能试验

为探究黏滞阻尼器的漏油对其力学性能影响,进行了不同漏油比例下的黏滞阻尼器性能试验[20]。试验设备为4 500 kN阻尼器试验机,最大位移为1 000 mm,峰值速度为1 m/s。该试验机包括了电液伺服控制系统、数据测量以及采集系统,可直接读取试验过程中的阻尼力、位移等数值。试验装置的总体布置如图2所示,黏滞阻尼器的外筒与设备的固定端连接,阻尼杆与作动头一端连接。

图2 漏油黏滞阻尼器性能试验Fig.2 Test of the viscous dampers with oil leakage

试验进行时环境温度为25℃。由于试验加载过程的持续时间只有几十秒至几分钟,因此可以认为环境温度保持25℃不变。由于阻尼器运动放热升温,因此在每个工况结束后对阻尼器进行降温处理,直至与室温相同再进行下一个工况的试验。

通过液压伺服静动载加载系统,对试验阻尼器进行简谐加载。试验的加载方式如表2所示,其中控制位移幅值为常数300 mm,速度幅值从50 mm/s逐渐增加到300 mm/s,其对应的加载频率可以由速度得到。

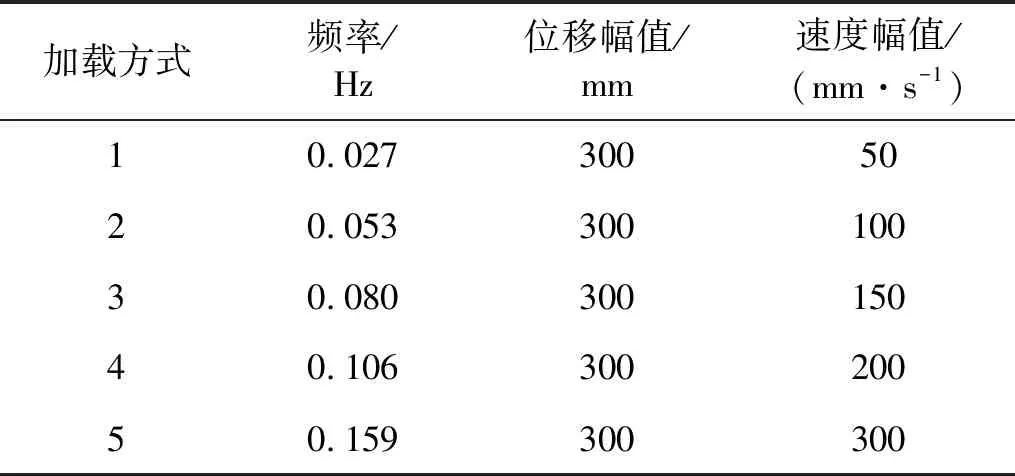
表2 试验加载方式

试验中,取3种不同的漏油比例,分别为0(即无泄漏),20%和40%。漏油比例通过从泄油孔中排出相应体积的油液加以控制。试验工况的命名方式为“漏油比例-加载方式”,如漏油比例为40%,加载频率为0.080 Hz(即加载方式3)的工况名称为“40%-3”。

不同漏油程度下的黏滞阻尼器的力-位移关系如图3所示。由图3(a)和(b)可知,所有漏油比例下,阻尼器的最大阻尼力随加载速度增大而增大。根据图3(c),当漏油比例不同但加载方式相同时,最大阻尼力基本一致,这意味着漏油几乎不会影响黏滞阻尼器的基本力学参数。将有无漏油情况黏滞阻尼器的滞回曲线进行对比,图3(c)中无漏油阻尼器的滞回曲线饱满,说明黏滞阻尼器在正常工作情况下具有良好的耗能能力;而漏油黏滞阻尼器的滞回曲线出现了无阻尼力的平台段,且漏油比例越高,平台段的长度越长。零力平台段的出现将减小滞回曲线的包络面积,因此漏油黏滞阻尼器的耗能能力明显减弱。该平台段主要由黏滞阻尼器工作初期压缩腔中气体排空导致。

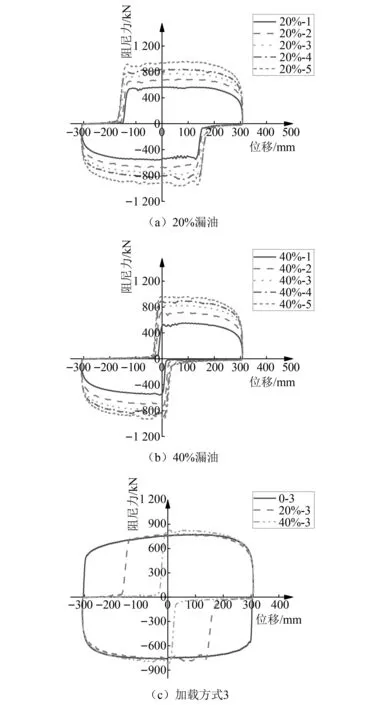
图3 漏油黏滞阻尼器试验滞回曲线Fig.3 The hysteresis curves of leaked viscous damper obtained by cyclic test

1.3 黏滞阻尼器的阻尼液黏温关系

温度影响黏滞阻尼器力学性能的主要原因是,不同的温度会引起硅油黏度的变化,从而影响黏滞阻尼器的力学性能,因此有必要建立阻尼器温度与硅油黏度之间的关系。

潘克非[21]为确定硅油在不同温度下的黏度,进行了硅油的黏温关系试验。对不同种类硅油在不同温度下测得的黏度进行了回归分析,假设黏度与温度的关系为指数形式

nη=KemT

(2)

式中:nη为指定温度下的黏度,cst;e为自然对数;T为温度,℃;K和m为待定系数。

根据试验测试结果,拟合出了理想黏度100～1 000 cst的硅油黏温关系,如图4所示。

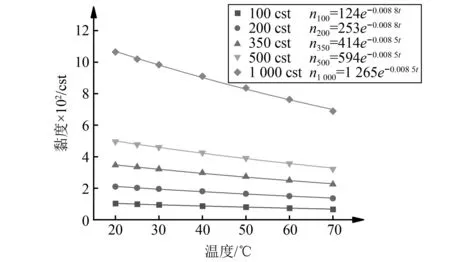
图4 各类硅油黏温关系曲线Fig.4 Viscousity-temperature curve of different silicon oil

观察比较所得黏温关系方程,系数与常温下硅油黏度的比值大致相同,均处于1.18～1.27,且该比值随着标定黏度的增加无明显规律,此处取其平均值1.228,即为标定黏度的1.228倍。对于常温时黏度较大的硅油,系数均为-0.008 5。因此,根据以上各类硅油的黏温关系式,可以认为当标定黏度为200 000 cst时,黏度随着温度变化的关系式为

n200 000=245 600e-0.008 5T

(3)

式中:n200 000为指定温度下200 000 cst硅油的黏度;T同样为温度。由于硅油为非牛顿流体,其实际黏度与剪切速率有关,此处计算出的黏度仅为该温度下的表观黏度。

2 黏滞阻尼器的流体仿真

2.1 黏滞阻尼器的有限元建模

根据表1中黏滞阻尼器的各项基本参数,在ANSYS/Design modeler中建立了阻尼器的计算流体力学模型。用ANSYS/Workbench中的Meshing模块对模型进行网格单元划分,采用结构化六面体网格,以提高网格质量和计算效率。计算域中包括234 877个节点,206 322个网格单元,如图5所示。将网格导入ANSYS中的Fluent模块进行计算流体力学分析,借助3D动网格技术,用UDF定义活塞面的正弦运动边界条件,采用基于压力的瞬态求解器进行分析。

图5 黏滞阻尼器有限元模型Fig.5 The finite element model of the fluid viscous damper

针对本研究中的漏油和温度两个影响因素,一方面,可用多相流模型中的Mixture来模拟漏油黏滞阻尼器中的油气混流现象,通过改变混合物中空气所占的比例来模拟漏油程度;另一方面,由于流变指数只与阻尼器孔隙或间隙的构造有关,故可认为仅温度变化时流变指数不变,此处取0.3。此时流体黏度仅受稠度系数和剪切速率的影响,可合理假设稠度系数的变化规律与黏度的变化规律相同,即通过调整不同温度下对应黏滞液体的稠度系数来体现温度对阻尼器工作的影响。

漏油黏滞阻尼器的仿真工况与试验工况相同。根据JT/T 926—2014《桥梁用黏滞阻尼器》[22],黏滞阻尼器的适用环境温度为-25～50℃,本研究中最低温度取-20℃,最高温度取40℃,间隔为20℃。温度仿真工况的加载方式与漏油试验相同,命名方式与漏油试验类似,记为“温度-加载方式”,例如温度为-20℃,加载频率为0.053 Hz(加载方式2)的工况名称为“-20℃-2”。

此外,为探究温度与漏油两种因素联合作用对黏滞阻尼器力学性能的影响,拟定仿真工况如表3所示。联合作用工况的命名方式为“温度-漏油比例-加载方式”,例如在20℃下,对漏油比例为20%的黏滞阻尼器用方式4进行加载,此时工况命名为“20℃-20%-4”。

表3 漏油-温度联合作用仿真工况

2.2 漏油影响下黏滞阻尼器仿真与试验结果对比

选取加载方式为1、3和5的工况,将仿真与试验结果进行对比,如图6所示。该仿真方法对于零力平台长度的模拟与试验结果十分接近。除平台长度外,还可观察到仿真与试验所得滞回曲线的形状和阻尼力峰值等特征也基本吻合,从而验证了仿真模拟的准确性,故可将该仿真模拟所得的结果作为后续进一步分析的基础。

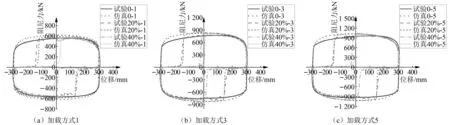
图6 漏油黏滞阻尼器试验与仿真滞回曲线对比Fig.6 Comparison between hysteresis curves of leaked viscous damper obtained by test and simulation

图7展示了加载方式3下,不同泄漏程度黏滞阻尼器的阻尼力-速度曲线的仿真结果。如图7所示,无泄漏时,速度与阻尼力呈对数关系,与式(1)规律相符。当阻尼器泄漏时,有部分曲线与横轴重合,此时活塞运动速度不为0,但阻尼器未产生阻尼力,即对应漏油阻尼器滞回曲线中的平台段。当漏油比例为20%时,速度达到130 mm/s后阻尼器恢复出力,而当漏油比例为40%时,只有当速度接近加载速度峰值150 mm/s时,阻尼器才开始发挥减震作用。这与阻尼力-位移曲线中,漏油程度越严重,平台长度越长的现象相吻合。

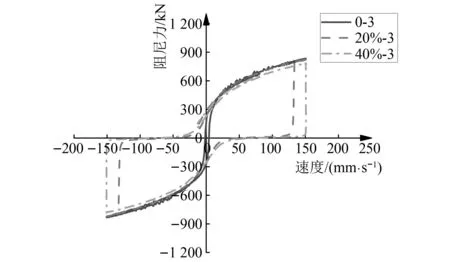
图7 漏油黏滞阻尼器仿真阻尼力-速度曲线Fig.7 The damping force-velocity curve of leaked viscous damper obtained by simulation

零力平台段的出现会影响阻尼器的实时工作性能,即阻尼器无法在外部振动荷载下立刻发挥作用,而存在一定的滞后。因此,平台段长度对于研究漏油黏滞阻尼器的实时减振/震效果具有十分重要的意义。

2.3 温度影响下黏滞阻尼器仿真结果

0和40℃下黏滞阻尼器的仿真滞回曲线如图8(a)和8(b)所示。可以看到所有工况下的力-位移曲线形状饱满,阻尼器具有较好的实时减振/震性能。与漏油工况类似,同一环境温度下,较好的实时阻尼性能加载速度越高,产生的最大阻尼力越大,曲线面积越大。

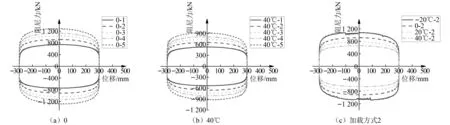
图8 不同温度下黏滞阻尼器仿真滞回曲线Fig.8 The hysteresis curves of viscous damper at different temperature

图8(c)所示为阻尼器加载方式相同但所在环境温度不同的滞回曲线。可以发现最大阻尼力与滞回曲线的面积随着温度升高而减小,这是由于硅油黏度随温度升高而减小,从而导致阻尼系数降低的缘故。当温度为-20℃、0、20℃和40℃时,对应的最大阻尼力分别为1 084 kN、968 kN、871 kN和658 kN,其消耗的能量分别为1.193MJ、1.010 MJ、0.855 MJ、0.723 MJ。这说明温度的变化对黏滞阻尼器的力学性能和耗能能力会产生较大的影响。

图9为加载方式4下,不同环境温度中的阻尼力-速度曲线。可以观察到,所有温度下速度与阻尼力均呈对数分布,但阻尼力峰值随着温度的升高而减小,与滞回曲线所示规律相同,即温度的变化不影响阻尼力与速度力学关系的基本形式,但关系式中阻尼器的基本力学参数会随着温度的变化而变化,因此将温度作为参数引入黏滞阻尼器的力学模型是十分有必要的。

2.4 漏油与温度联合作用下黏滞阻尼器仿真结果

对表3中列出的4种工况进行了有限元仿真建模和分析,在加载频率为0.106 Hz时(加载方式4),漏油与温度联合作用下黏滞阻尼器的滞回曲线如图10所示。可以观察到,当漏油比例相同但环境温度不同时,图示零力平台段长度几乎完全相同,因此温度变化不会引起平台长度的变化,可以认为滞回曲线的平台长度仅与漏油程度有关。

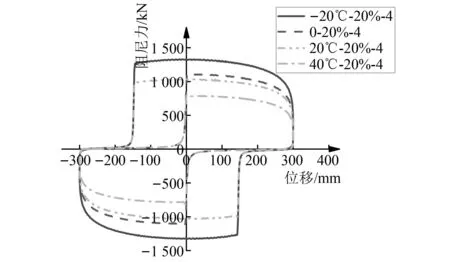
图10 漏油与温度联合作用下黏滞阻尼器滞回曲线Fig.10 The hysteresis curves of leaked viscous damper at different temperatures

以环境温度为0°,加载方式4为例,将同一温度作用下有无漏油情况的最大阻尼力进行对比,无漏油时最大阻尼力为1 137 kN(该值可由图8(a)得到),漏油比例为40%时最大阻尼力为1 116 kN,两者误差仅为1.84%,再次印证了阻尼器最大出力与漏油比例无关,仅受环境温度改变的影响。据此,可以基本确定漏油与温度两种因素对阻尼器力学性能的影响是相互独立、不耦合的。因此,在后续建立阻尼器力学模型时,可以将漏油与温度两种因素单独考虑,建立单因素影响下的力学模型后,直接叠加得到二者联合作用下的力学模型。

3 黏滞阻尼器性能演变的力学模型

3.1 考虑漏油的阻尼力模型

根据试验与仿真所得结果,可以得出不同工况下的最大阻尼力,对式(1)两边取对数可得

lnF=lnC+αln|v|

(4)

令Y=lnF,X=ln|v|,A=lnC可以将其转化为线性形式

Y=A+αY

(5)

根据试验与仿真所得结果,可以得出5种加载方式下的最大阻尼力,且加载速度已知,可通过线性回归分析,计算出每一种漏油比例或环境温度下,不同加载方式对应的阻尼系数和速度指数,计算方法为

(6)

(7)

据此,可以识别出每一种漏油比例和环境温度下阻尼器的阻尼系数和速度指数,如表4所示。由表4可知,每一种漏油比例下,阻尼系数C和速度指数α与黏滞阻尼器设计值的差值均在10%以内,因此可以认为漏油几乎不会影响黏滞阻尼器的基本力学参数。

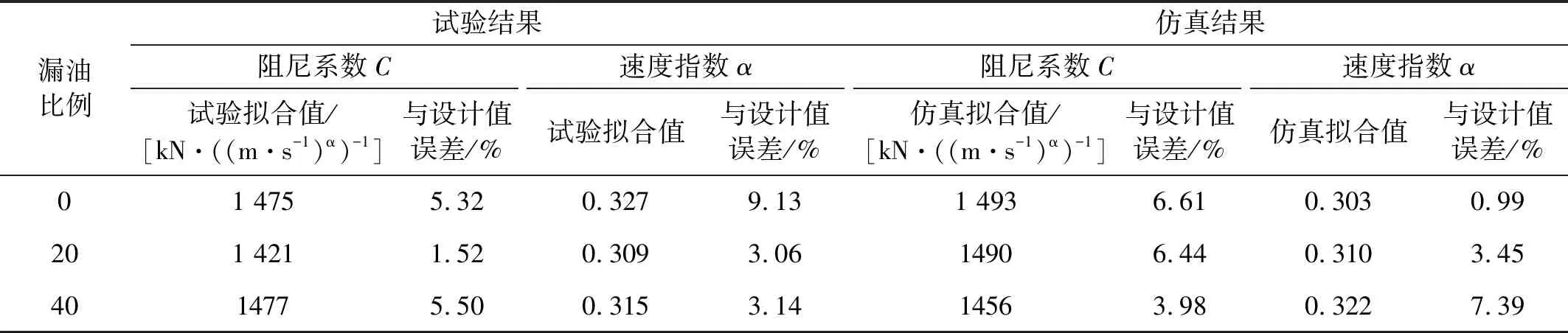
表4 漏油黏滞阻尼器基本力学参数

然而,漏油黏滞阻尼器的滞回曲线出现了无阻尼力的平台段,同一漏油比例下平台长度几乎不变,且其长度随漏油比例增加而增加。本文中,平台段的起止点分别为,阻尼器出力小于阻尼力峰值10%时对应的位移,和最大位移300 mm。黏滞阻尼器在不同漏油比例下,试验及仿真在同一漏油比例下的平台段长度如表5所示。

表5 黏滞阻尼器平台段长度

对试验和仿真得出的平台长度进行线性回归分析,考虑未漏油时平台长度为0,故设定截距为0,最终确定平台段长度与漏油比例的关系式为

l=702.057p

(8)

式中:l为平台段长度;p为漏油比例。由于在实际工程中,当黏滞阻尼器漏油比例超过40%时,其减震性能及耗能能力已受到严重损害,需要进行更换,因此该公式仅适用于漏油比例40%以下的情况。此外,所选试验阻尼器的设计最大位移为300 mm,但是其内腔的总长为740 mm(见图1(a)),即可运动最大位移为370 mm。而漏油程度是基于阻尼器总油量计算的,即基于740 mm进行计算。因此式(8)中的常数系数接近内腔总长,但由于部分空气会溶解于硅油中,导致系数略小于内腔总长。

为验证该公式的适用性,对漏油程度为10%的黏滞阻尼器进行了有限元仿真,得出平台段长度为71.718 mm,而根据式(8)计算得出相应的平台长度为70.206 mm,与仿真值误差仅为2.15%,因此,可以认为该公式能够用于计算不同漏油比例下的平台长度。

漏油黏滞阻尼器的力学模型可表示为一个两阶段的分段函数模型。当阻尼器的位移小于平台段长度时,活塞首先挤压空气,滞回曲线处于平台段,此时阻尼力为0;当阻尼器位移超过平台段长度后,硅油开始通过孔隙和间隙,阻尼器恢复出力,各项力学参数与设计值相同。漏油黏滞阻尼器的阻尼力为

(9)

式中:Fi为i时刻的阻尼力;vi-1为i-1时刻对应的速度;xi-1为i-1时刻对应的位移;xr为阻尼器反向运动最后一个时刻对应的位移;l为阻尼器滞回曲线的平台段长度,可根据式(8)计算得出。

3.2 考虑温度变化的阻尼力模型

同理3.1节,通过不同温度下仿真得出的最大阻尼力,可拟合出不同温度下阻尼器的阻尼系数、速度指数及其与设计值的差值,如表6所示。由表6可知阻尼系数明显随温度的升高而减小,且当温度低于设计温度25℃时,阻尼系数大于设计值1 400 kN/((m/s)α),温度高于25℃时,阻尼系数小于设计值。此外,速度指数α与设计值0.3的差值均在5%以内,这是由于进行仿真分析时未调整流变指数导致的,速度指数作为流变指数的宏观体现,其值也不会发生改变。综上,温度效应仅影响阻尼系数C的大小,而几乎不影响速度指数的值。

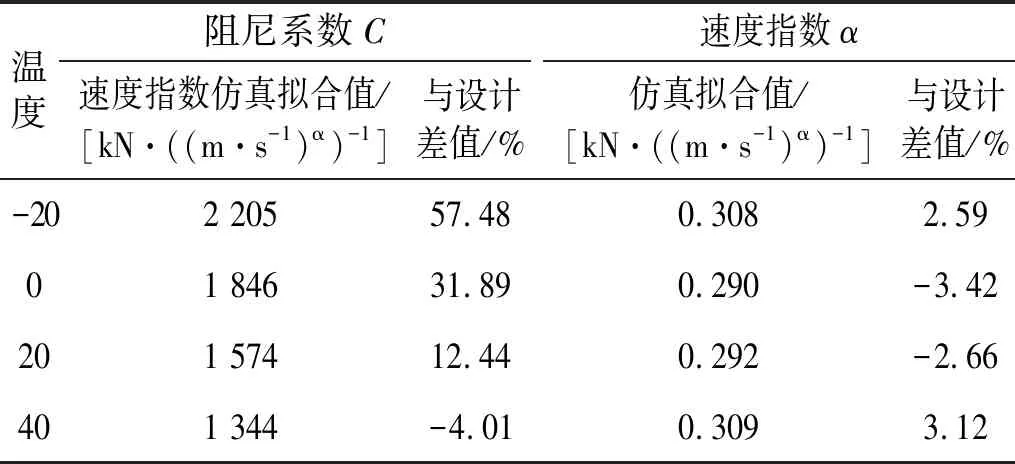
表6 温度变化下黏滞阻尼器基本力学参数

观察到阻尼系数的下降趋势随着温度升高趋于平缓,且阻尼力的大小主要取决于黏滞液体的黏度,故选择与硅油黏温关系相同的指数形式作为阻尼系数拟合的函数类型,对以上数据进行回归分析,可得到阻尼系数随环境温度变化的关系

CT=1 857.780e-0.008 4T

(10)

式中:CT为不同温度下的阻尼系数,T为环境温度,℃。

把温度作为一项参数引入黏滞阻尼器的力学模型,即将不同温度下的阻尼系数CT代入式(1),可以得到温度变化下的阻尼力公式

FT=CTsgn(v)vα

(11)

式中:FT为不同温度下的最大阻尼力;CT为不同温度下的阻尼系数,其数值通过式(10)计算得出,其余参数含义同式(1)。

3.3 漏油和温度联合作用下的阻尼力模型

由于漏油和温度两种因素对黏滞阻尼器力学性能的影响不会相互耦合,故将两公式直接结合,即可得到在漏油与温度联合作用下黏滞阻尼器性能演变的力学模型,如式(12)所示。其形式为以速度和温度为自变量的分段函数,在阻尼器位移小于其漏油比例对应的平台段长度时,阻尼力为0,当位移超过平台长度后,阻尼器恢复出力,其值与温度和速度相关。

(12)

式中,FiT为漏油与温度联合作用下性能演变黏滞阻尼器在i时刻输出的阻尼力,其余参数含义同前文。

3.4 黏滞阻尼器性能演变模型验证

选取三种环境温度与漏油比例联合作用的典型工况(工况20℃-0-1,工况40℃-20%-3和工况0-40%-4),将按提出的阻尼器性能演变的力学模型所得的力-位移曲线与对应工况的仿真滞回曲线进行对比,结果如图11所示,模型滞回曲线与仿真所得滞回曲线十分吻合。通过该曲线计算出每个工况对应的阻尼力和耗能,如表7所示,模型与仿真结果之间的误差均在6%以内,因此可以认为该力学模型是合理的。

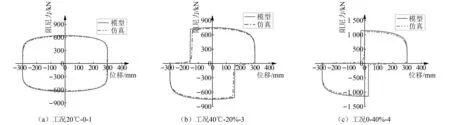
图11 联合作用下黏滞阻尼器力学模型与仿真滞回曲线对比Fig.11 The comparison among hysteresis curves of viscous dampers of combined oil leaking and temperature effects obtained by mechanical model and simulation

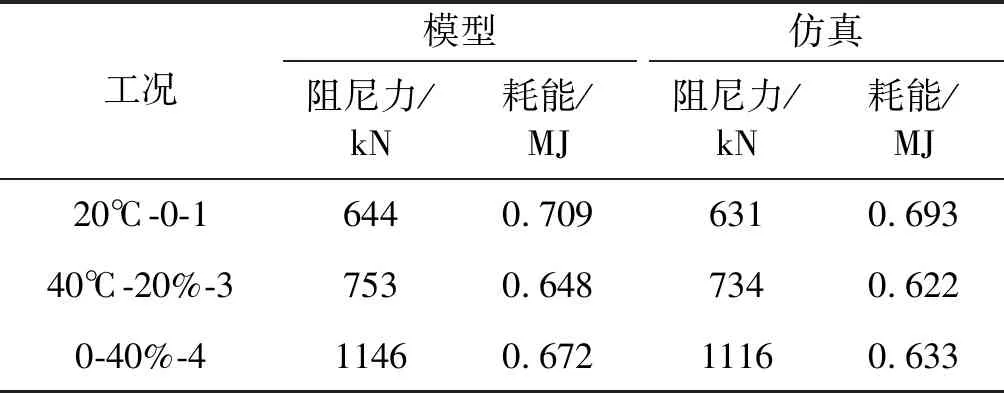
表7 漏油与温度联合工况阻尼力与耗能

4 结 论

为探究黏滞阻尼器的漏油和温度对其力学性能的影响,本文对某特定型号不同漏油程度的黏滞阻尼器开展了滞回试验;对温度作用下的硅油黏度进行了分析;对不同漏油程度与环境温度下的黏滞阻尼器进行了流体动力学仿真;根据试验与仿真所得力学参数和滞回曲线,建立了漏油与温度联合作用下黏滞阻尼器性能演变的力学模型。主要结论如下:

(1) 漏油对黏滞阻尼器力学性能的影响主要体现为滞回曲线出现零力平台段,且漏油比例与平台段长度成正比。但当阻尼器位移超出平台长度后恢复出力,泄漏对黏滞阻尼器的阻尼力和力学参数(阻尼系数C和速度指数α)几乎无影响,因此可采用分段函数表征漏油下的阻尼力。

(2) 通过硅油的“黏温关系”可以推导得到,温度的升高会导致硅油黏度的下降,从而影响黏滞阻尼器的阻尼系数,故将温度作为参数引入阻尼系数,得到不同温度下的黏滞阻尼器力学模型。

(3) 漏油和温度作用对黏滞阻尼器力学性质的影响不互相耦合,因此将考虑漏油的阻尼力模型与温度作用下的阻尼力模型综合可得二者联合作用下黏滞阻尼器性能演变的力学模型,并与仿真结果进行对比,验证了该模型的有效性和正确性。