基于勒让德-扫描法的机械结合部法向接触刚度区间分析

刘 勇, 渠 杰, 张 青, 王大伟, 闫方超

(1. 中国民航大学 航空工程学院,天津 300300;2. 天津布尔科技有限公司,天津 200392)

机械零件间紧密接触的结合部分被称为“机械结合部”,结合面间的接触实际上是两个粗糙表面间大小不一的微凸体之间的接触[1]。航空发动机是由上万个零件组成的复杂机械系统,其内部存在大量的机械结合部,影响航空发动机的整机动态特性。因此,在研究航空发动机的整机动态特性时,将结合部的法向接触刚度考虑在内就显得尤为必要。

目前关于结合部法向接触刚度模型的研究大多基于确定性假设,但在实际工程中,受材料表面的不均匀性、加工误差、测量误差等因素的影响,粗糙表面微观形貌参数会存在较大的不确定性,导致结合部法向接触刚度也存在不确定性。Fukuoka[2]的研究指出结合部法向接触刚度的不确定性是连接结构刚度离散性的主要诱因,而传统的确定性接触刚度模型无法准确预测结合部法向接触刚度。因此,考虑粗糙表面形貌参数的不确定,建立结合部法向接触刚度的区间模型,对于研究结合部法向接触刚度以及确保航空发动机的稳定运行都具有至关重要的作用。

粗糙表面接触建模是法向接触刚度研究的基础。Greenwood等[3]以Hertz接触理论为基础,建立了经典弹性接触(Greenwood-Williamson,GW)模型,为粗糙表面统计学接触研究提供了可靠的支撑。GW模型存在诸多缺点,为进一步完善GW模型,许多学者针对于GW模型的不足进行了修正[4-6]。基于GW模型及其改进模型,一些学者针对于结合部法向接触刚度进行了研究。庄艳等[7]研究了微凸体粗糙峰之间的侧向接触,建立了考虑微凸体实际大小和空间分布的法向接触刚度计算模型,并将实测的表面形貌参数代入所建立模型中,通过与试验对比验证了所提出模型的有效性。田小龙等[8]建立了考虑粗糙表面微凸体相互作用的法向接触刚度统计学模型,在此基础上研究了不同塑性指数下微凸体之间相互作用对法向接触刚度的影响。Yin等[9]将微凸体变形阶段重新划分,建立了考虑硬度变化的法向接触刚度统计学模型。考虑到传统法向接触刚度模型表达式复杂,难以获得接触载荷与法向接触刚度之间的之间关系,Xiao等[10]基于不同微观接触模型的数值模拟结果,建立了关于法向载荷的法向接触刚度显式近似表达式。Bai等[11]考虑加工表面的实际形貌并基于高斯分布建立了更符合真实情况的虚拟表面,通过计算微凸体变形与接触力的关系,建立了粗糙表面法向接触刚度的统计学模型。综上所述,关于结合部法向接触刚度统计学模型的研究大多基于确定性假设,忽略了表面微观形貌参数的不确定性。因此,为了更深入研究结合部法向接触刚度,需要考虑表面形貌参数不确定性的影响。

在不确定性研究中,由于区间算法只需定义不确定变量的上下边界,无需获取不确定变量的精确概率分布,并且对试验数据依赖性小,区间算法被广泛用于不确定性研究中[12-15]。基于Legendre多项式所建立的区间代理模型可避免复杂运算并且计算效率较高,在多体动力学和转子动力学领域取得了应用[16-17]。与传统的切比雪夫包络函数法相比,基于Legendre多项式的扫描法求解精度更高[18]。目前利用区间算法对于连接结构的研究大多集中于宏观动力学方面[19-20],采用区间算法对于结合部接触刚度进行研究的报道较少,Zhao等[21]基于测量所得的粗糙表面分形参数,并引入切比雪夫区间法,建立了粗糙表面法向和切向接触刚度的分形区间模型。在此基础上,李玲等[22]引入矩谱法计算了表面微观形貌参数区间,并分析了微观形貌参数对于粗糙表面法向接触刚度区间的影响规律。上述关于粗糙表面接触刚度的研究,作者重点关注结合部法向接触刚度的区间表征与分析,所建立的接触刚度区间范围不够精确,导致模型的实际参考价值不足。

有鉴于此,本文基于勒让德-扫描法(Legendre scanning method, LSM)建立机械结合部法向接触刚度区间模型并进行求解,即基于勒让德多项式和粗糙表面统计学接触刚度模型,建立考虑粗糙表面形貌参数不确定的法向接触刚度区间模型,将微凸体曲率半径、分布密度、微凸体高度方差视为区间变量,并采用扫描法求解区间模型。以45号钢为算例,通过与庄艳等研究中的法向接触刚度试验结果以及传统区间算法求解结果进行对比,验证了本文建立接触刚度区间模型的有效性和准确性。基于该模型,分析了不同区间变量对结合部法向接触刚度区间的影响规律。

1 粗糙表面法向接触刚度模型

两个粗糙表面的接触如图1(a)所示,可利用一个等效粗糙面与和一个光滑刚性平面的接触来代替[23]。在图1(b)中:β为微凸体曲率半径;z为微凸体高度,且有z=ω+d;ω为微凸体变形量;d为光滑刚性平面与微凸体平均高度之间的距离。一般认为,随着接触压力的增加,微凸体变形经历三个阶段:弹性、弹塑性和塑性变形。

图1 粗糙表面接触示意图Fig.1 Rough surface contact

当载荷较低或者接触变形量ω较小时,微凸体发生弹性变形。接触载荷pe、接触面积Ae、平均接触压力Ne与ω之间的关系可利用Hertz弹性接触理论描述

(1)

Ae=πβω

(2)

(3)

式中:E*为两个表面接触的等效弹性模量,E*=E/(1-μ2);μ为材料的泊松比。

高载荷下,微凸体发生完全塑性变形,该阶段平均接触压力pp、接触面积Ap和接触载荷Np可由AF模型[24]表示

pp=H

(4)

Ap=2πβω

(5)

Np=2πβHω

(6)

式中,H为材料硬度,H与屈服强度δy相关,满足H=2.8δy。

金属材料表面受到的接触应力超过屈服强度时,微凸体存在弹塑性变形状态。KE弹-塑性接触模型考虑了微凸体的弹塑性变形,更贴近真实接触状态。基于KE接触模型得到的接触载荷F(hn)和法向接触刚度K(hn)表达式为

(7)

(8)

式中:hn为粗糙面高度均线与刚性平面之间的距离,下标“n”为对变量进行无量纲化;zn为无量纲参数;N为粗糙表面参与接触的微凸体总数,N=ηAn(An为名义接触面积,η为微凸体分布密度);σ为微凸体表面高度方差,σ与微凸体高度分布标准差σs、粗糙表面高度分布函数φ(z)之间满足以下关系

(9)

2 考虑形貌参数不确定性的结合部法向接触刚度区间模型

由式(8)可看出,影响结合部法向接触刚度的参数较多,传统的统计学接触模型为简化计算,假设表面微凸体的曲率半径相同,该假设与实际情况不符。在机加工表面上,微观形貌参数的变化会使结合部法向接触刚度产生较大的不确定性,不利于结合部法向接触刚度的分析和优化。为此,本文基于勒让德多项式和KE弹塑性接触刚度模型,建立考虑表面形貌参数不确定性的接触刚度区间模型。

2.1 勒让德多项式

一个定义域是[-1,1]的函数f(x)可以近似采用p阶截断勒让德多项式表示[25]

(10)

式中:fi为截断勒让德多项式常系数;Li(x)为勒让德多项式。勒让德多项式满足以下递推关系

(11)

同理,对于具有多个不确定性输入参数的多元函数f(x1,x2,…,xm),可以使用多维Legendre多项式进行近似表征

f(x1,x2,…,xm)≈fL(x1,x2,…,xm)=

(12)

计算上述高维问题所需插值点数量极多,为减少计算量,提升计算效率,对式(12)化简可得

(13)

式中,ψi(x)为i个一维多项式的张量积,可由下式进行计算

ψi(x)=Li1,i2,…,im(x1,x2,…,xm)=
Li1(x1)Li2(x2)…Lim(xm)

(14)

式中,γi为勒让德多项式系数矢量,表达式为

γi=(TTT)-1TTY=[γ0,γ1,…,γk-1]T

(15)

式中:Y为插值点处的模型输出矢量;T为勒让德转换矩阵。基于上述公式,T可表示为

(16)

(17)

2.2 考虑形貌参数不确定性的法向接触刚度区间模型

对粗糙表面进行法向接触刚度分析时,首要任务是确定真实粗糙表面形貌参数,即微凸体等效曲率半径β,微凸体分布密度η,微凸体表面高度方差σ。由于区间算法具有对输入参数的依赖性较小、无需获取输入变量的具体概率分布等优点,被广泛用于处理不确定性问题。因此,本文把上述三个参数视作区间变量xj(j=1,2,3)

(18)

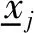
(19)

根据式(8)、式(9)和式(12),可建立考虑形貌参数不确定的结合部法向接触刚度区间模型,表达式为

(20)

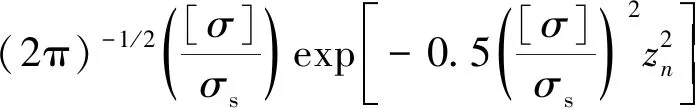
(21)

为简化模型提高计算效率,结合部法向接触刚度区间模型可由下式近似表示

(22)

式中:fL([ε])为基于勒让德多项式计算得到的法向接触刚度;ε=[ε1,ε2,ε3]为区间变量标准化后的矢量,εj(j=1,2,3)与区间变量xj(j=1,2,3)之间存在以下关系

(23)

输出变量,即法向接触刚度区间的不确定度λK可定义为

(24)

式中:Ku和Kl分别为法向接触刚度区间的上界和下界;λK的取值范围是[0,1],不确定度越小,说明所建立法向刚度区间的精度越高。

一般情况下可利用传统勒让德区间算法计算接触刚度的上下边界,但是传统的区间算法精度有限,在求解多个不确定变量的问题时“包裹效应”会导致区间解过度放大,影响区间解的精度。为此,采用扫描法[26]对基于勒让德多项式建立的粗糙表面法向接触刚度区间模型进行求解。

2.3 求解结合部法向接触刚度区间模型

对于式(22),在计算ψi([ε])时,由于“包裹效应”的存在,会产生估计值偏高的现象,导致计算结果偏大。因此可通过扫描法直接计算fL([ε])的最值以获取法向接触刚度的上界和下界。扫描法可以很好地控制“包裹效应”,并且当区间变量的个数m≤3时,扫描法可精确获得区间模型的边界。基于扫描法的区间上下界求解公式为

(25)

图2为求解结合部法向刚度区间模型的算法流程。以下是模型求解步骤:

图2 计算流程图Fig.2 Flowchart of computation process

步骤1输入区间向量的维数及Legendre多项式阶数(j、p)。

步骤2将区间变量进行表示,同时根据式(17)确定插值点个数,并通过式(13)～式(16)利用一维多项式的张量积构造勒让德转换矩阵。

步骤3运用Matlab软件设计循环,在i+1个步骤中,根据式(20)～式(21)分别求解给定插值点处的结合部法向接触刚度值,基于求解结果构造插值点处的模型输出矢量Yi+1。将Yi+1代入式(15)中,结合步骤2得出的勒让德转换矩阵,可构造勒让德多项式系数矢量γi+1。

步骤4基于上述参数,对于矩阵γi+1的每一列元素采用扫描法以及传统区间算法求解法向接触刚度区间模型,得到对应的法向接触刚度边界。

步骤5重复步骤3、步骤4直至循环结束,可得到结合部法向接触刚度区间。

3 模型验证

3.1 与试验结果对比

为验证基于LSM的接触刚度区间模型的有效性,将模型结果与庄艳等研究中试验测得的刚度值进行对比,结果如图3所示。试验所用材料为45号钢,材料属性参数为:弹性模量E=200 GPa,泊松比v=0.29,材料硬度H=2 025 MPa。庄艳等研究测量得到的45号钢表面微观形貌参数区间范围,如表1所示。

表1 表面形貌参数区间分布表

图3 法向接触刚度理论区间与试验结果对比Fig.3 Comparison of theoretical intervals of normal contact stiffness and experimental results

如图3所示,随着无量纲接触距离ωn的减小,基于本文方法得出的法向接触刚度区间与试验数据基本吻合,证明了本文建立区间模型的有效性。当接触间隙为0.4时,本文所建立结合部刚度区间模型的计算值偏离试验值的主要原因在于:未充分考虑微凸体之间的相互作用;忽略了材料自身形变时的强化。

3.2 与现有不确定接触模型对比

为验证基于LSM的接触刚度区间模型的准确性,将模型结果与基于切比雪夫包络函数法所得结果进行对比。如图4所示,LSM和切比雪夫包络函数法均可获得较可靠的结果。基于LSM所得法向接触刚度区间不确定度是0.263,利用切比雪夫包络函数法求解所得法向接触刚度区间不确定度是0.468,说明LSM相较于切比雪夫包络函数法在法向接触刚度区间模型计算时具有更高的精度。

图4 两种区间算法计算结果对比Fig.4 Comparison of calculation results using different interval algorithms

3.3 与传统区间算法对比

根据表1中的数据,由式(20)～(25)得到法向接触刚度区间。为方便对比,采用传统区间算法对式(22)进行求解。如图5所示,对结合部法向接触刚度区间模型进行求解时,扫描法和传统区间算法均可获得较可靠的结果。利用传统区间算法求解所得法向接触刚度区间的不确定度为0.633,利用扫描法求解所得法向接触刚度区间的不确定度为0.263,求解所得区间的不确定度大幅降低,说明扫描法相较于传统区间算法在求解法向接触刚度区间模型时具有更高的精度。

图5 不同算法下法向接触刚度随ωn变化关系Fig.5 Effect of contact gap on normal contact stiffness under different algorithms

法向接触刚度区间上下界之差(即界差)与接触间隙之间的关系,如图6所示。随着接触间隙的减小,界差逐渐增大,扫描法计算得出的界差小于勒让德法得出的界差。这是由于扫描法是基于密集网格样本,计算不同参数区间内所有采样点的响应,从而获得较为精确的法向接触刚度区间模型边界。因此,扫描法可有效抑制区间扩张导致的“包裹效应”。

图6 扫描法和区间算法计算法向接触刚度界差对比Fig.6 Comparison of the boundary difference calculated by scanning method and interval algorithm

结合上述验证,进一步说明了本文建立区间模型的有效性和准确性。最后基于LSM分析了表面形貌参数对结合部法向接触刚度区间的影响规律。

4 分析与讨论

微凸体分布密度(η)、微凸体曲率半径(β)、微凸体表面高度方差(σ)分别为区间参数时,采用LSM所得法向接触刚度变化范围如图7～图9所示。由图7～图9可知,不同区间变量对法向接触刚度的影响不同。如图7(a)所示,结合部法向接触刚度变化范围受微凸体分布密度(η)的影响较小。图7(b)表明随着微凸体分布密度的增大,不同载荷下的结合部法向接触刚度值也相应增加,但变化不明显。造成上述现象的原因是,在相同接触间隙下,当微凸体分布密度增大时,单位面积上实际参与接触的微凸体数量增多,但由于微凸体曲率半径较小,真实接触面积变化不明显,所以结合部法向接触刚度范围受微凸体分布密度(η)的影响较小。

图7 η对法向接触刚度区间影响Fig.7 Influence of η on normal contact stiffness interval

如图8(a)所示,结合部法向接触刚度变化范围受微凸体曲率半径(β)的影响较明显。图8(b)表明随着微凸体曲率半径的增大,不同载荷下的结合部法向接触刚度值也相应增加且变化较明显。这是由于当微凸体曲率半径变化时,相同接触间隙下真实接触面积的变化较明显,真实接触面积的改变会影响接触刚度,导致结合部接触刚度呈区间变化。

图8 β对法向接触刚度区间影响Fig.8 Influence of β on normal contact stiffness interval

如图9(a)所示,结合部法向接触刚度变化范围受微凸体表面高度方差σ的影响最显著。图9(b)表明随着微凸体表面高度方差σ的增大,不同载荷下的结合部法向接触刚度值也相应减小,并且变化较为明显。这是因为σ影响粗糙表面微凸体高度分布,σ增大时,表面粗糙度增加,微凸体与接触表面之间的真实接触面积减小,从而导致接触刚度减小。由图7～图9可以看出,相较于微凸体曲率半径和微凸体分布密度,表面高度方差对于法向刚度区间的影响更为显著。

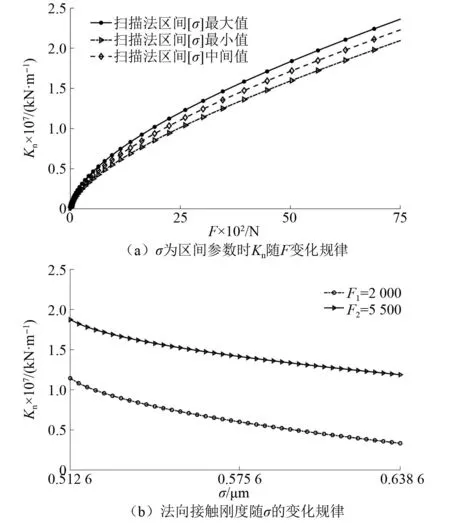
图9 σ对法向接触刚度影响Fig.9 Influence of σ on normal contact stiffness interval

5 结 论

(1) 考虑粗糙表面微观形貌参数的不确定性,基于勒让德多项式和传统KE弹塑性接触刚度模型,建立了结合部法向接触刚度区间模型。

(2) 采用基于勒让德多项式的扫描法对上述区间模型进行求解,并与传统区间算法求解结果进行了对比。结果表明,两种方法对结合部法向接触刚度值的估计均较为可靠,但是扫描法相较于传统区间算法在求解法向接触刚度区间模型的精度上有明显优势,使不确定度由原来的0.633减小到0.263。

(3) 以45号钢为例进行试验验证,可看出采用勒让德扫描法计算所得法向接触刚度区间结果与宏观接触刚度试验结果具有相同变化趋势且预测准确性较高。利用LSM建立并求解法向接触刚度区间模型可为航空发动机的结合部设计提供参考。

(4) 将区间变化的表面微观形貌参数代入粗糙表面法向接触刚度区间中并利用扫描法求解。结果表明,微凸体表面高度方差对结合部法向接触刚度区间的影响最大,微凸体曲率半径次之,影响较小的是微凸体分布密度。