轴流式水轮发电机组不对中-碰摩耦合故障振动特性分析

张雷克, 蔚建辉, 王雪妮2,, 张金剑, 马震岳, 邓显羽

(1. 太原理工大学 水利科学与工程学院,太原 030024;2. 河南省黄河流域水资源节约集约利用重点实验室,郑州 450046;3. 大连理工大学 建设工程学部,辽宁 大连 116023;4. 中水东北勘测设计研究有限公司,长春 130021)

旋转机械被广泛应用于能源开发、运输、国防等领域,其核心部件转子系统往往因加工精度及安装误差等造成不对中故障的出现。相关资料显示,超过70%的旋转机械故障由不对中引起或与之相关[1],其中多数因联轴器不对中所致。除不对中外,碰摩是旋转机械故障的另一典型代表,由于现代转子系统不断向小间隙、高转速和高负载方向发展,碰摩风险大大增加。当系统发生不对中或碰摩故障时,轻则会导致机组异常振动,影响设备正常使用;重则会造成设备过度损伤进而引发灾难性事故。因此,不对中及碰摩故障下转子系统的动力特性研究一直都是国内外相关学者的研究重点,且经数十年发展,取得了丰硕的成果[2-11]。

随着相关研究的不断深入,人们逐渐发现单一不对中或碰摩故障已无法充分揭示隐藏在转子系统内部的全部动力学特性,故将两者结合并考虑彼此之间的相互影响逐步进入了广大研究者的视野。黄志伟等[12-13]提出了具有不对中和碰摩耦合故障的水轮发电机组转子系统模型,采用数值方法分析了该系统随不对中量等参数变化的动态行为。朱拥勇等[14]引入转子间的位移约束,推导了非稳态油膜力和碰摩力作用下偏角不对中转子系统的运动微分方程,分析了系统横向振动特性。随后,伍小莉等[15]基于平行不对中-碰摩耦合故障下转子-滚动轴承系统动力学模型,探讨了不对中程度对系统振动特性的影响,在此基础上,进一步研究了不同支承条件下转子振幅的变化规律[16]。以航空发动机为研究对象,靳玉林等[17]研究了联轴器不对中及叶片-机匣碰摩故障下转子系统的响应特征,并通过试验测试验证了结果的准确性。Xie等[18]构建了不对中-碰摩耦合双转子系统模型,研究了系统在不同参数变化下的动态响应,并指出特征频率分量有助于转子系统耦合故障的诊断。针对转子系统不对中-碰摩耦合故障问题,李志农等[19]利用非线性输出频率响应函数对转子系统的不对中程度进行了识别。Liu等[20]建立了柴油发电机模型,采用平滑伪维格纳-维尔分布研究了系统在偏角不对中和碰摩故障情况下的振动响应。研究表明,伪维格纳-维尔分布谱在具有不同故障的旋转系统加速度响应之间存在明显差异。

从上述研究中可以发现,针对不对中和碰摩耦合故障下转子系统振动特性的分析与讨论已颇为丰硕,然而,其研究对象主要集中于高速、卧式旋转机构,对以水轮发电机组为代表的低速、立式布置系统研究则较为有限。黄志伟等对立式水轮发电机组开展了不对中-碰摩耦合故障激励下系统动态特性的讨论,但其所建模型未考虑转轮叶片的影响。Thiery等[21]针对转轮叶片与转轮室碰摩现象进行了详细讨论,但未将联轴器不对中纳入整体研究范畴。实际上,因旋转部件质量不平衡、轴系不对中等故障导致转轮叶片与转轮室接触是一种十分严重的碰摩现象。如能综合考虑旋转轴系不对中及动、静件细部碰摩因素,建立不对中-碰摩耦合故障下转子-转轮系统运动微分方程,据此得到的分析结果将更加接近工程实际,进而提高轴流式水轮机组在机械和电磁振源下故障识别的精度。

鉴于此,本文基于运动几何关系,推导了轴流式水轮机转轮叶片与转轮室接触的碰摩力表达式。在此基础上,建立了考虑碰摩、不对中、不平衡磁拉力等机电故障影响下轴流式水轮发电机组转子-转轮系统振动模型。采用Floquet理论探讨了不同转速下系统的周期解稳定性,利用数值分析手段研究了偏角变化对转子、转轮的影响。相关结论可为轴流式水轮发电机组轴系动力学特性分析和机组安全稳定运行提供参考。

1 轴流式水轮发电机组模型

具有联轴器偏角不对中的轴流式水轮发电机组模型如图1所示,其由上导轴承、发电机转子、定子、下导轴承、联轴器、水导轴承、轮毂、转轮叶片、转轮室等结构组成。

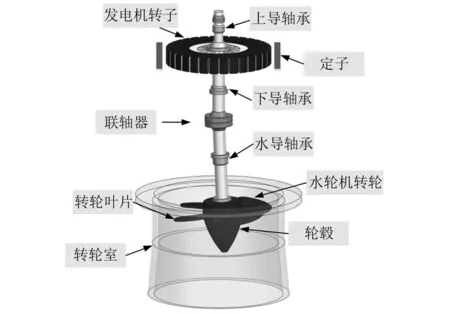
图1 轴流式水轮发电机组三维示意图Fig.1 Three-dimensional diagram of axial flow hydrogenerator set

为便于分析,将机组轴系简化为如图2所示的结构模型。图2中:O1、O2分别为转子、转轮形心;m1、m2分别为转子和转轮轮毂的质量;m0为单个转轮叶片的质量;kr1和kr2分别为转子、转轮处的碰摩刚度;α为不对中偏角;l1为转子形心至联轴器的距离;l2为联轴器到转轮形心的距离;Fx1_ump及Fy1_ump分别为发电机转子在x、y平面内的不平衡磁拉力;Px1_rub、Py1_rub和Fx2_rub、Fy2_rub分别为发电机转子和水轮机转轮在x、y方向所受碰摩力。

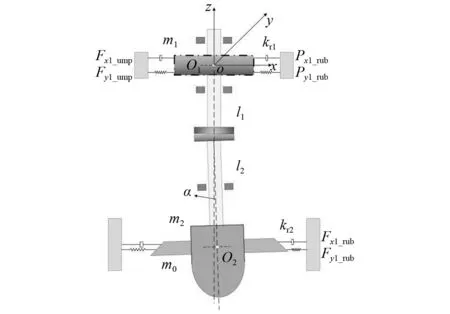
图2 轴流式水轮发电机组轴系模型简化示意图Fig.2 Simplified diagram of shafting model for axial flow hydrogenerator set

1.1 转轮叶片碰摩力

水轮机转轮叶片碰摩示意图,如图3所示。考虑到转轮室由混凝土支撑固定,故假定转轮室为刚性,转轮室外环为柔性,叶片为有均匀质量的刚性悬臂梁,仅考虑接触过程转轮室外环的变形。a点为叶片与转轮室外环最初接触位置,b点为叶片与转轮室外环最终接触位置,当叶片与转轮室外环发生碰摩时,叶尖侵入外环内部,此时碰摩力包括切向摩擦力Fti和径向接触力Fni。

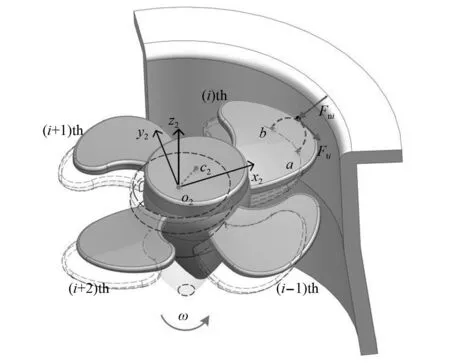
图3 叶片与转轮室外环碰摩示意图Fig.3 Schematic diagram of rubbing between blade and runner outer ring

转轮室外环内径为

r2=R2+L2+B

(1)

式中:R2为轮盘半径;L2为叶片长度;B为碰摩间隙,B=δ2-L2×sinα,δ2为叶尖与转轮室外环初始间隙。

为便于计算,忽略叶片初始位置角的影响,假定第1个叶片的位置角以x轴为起点,故其数值为0°。n为叶片数,φ=ωt为旋转角速度,则第i个叶片的位置角为

φi=ωt+2(i-1)π/n

(2)

其叶片叶尖坐标为

(3)

式中,x2,y2分别为转轮在x、y方向上的位移,则第i个叶片叶尖在转轮旋转时的半径为

rti={[x2+(R2+L2)cosφi]2+
[y2+(R2+L2)sinφi]2}1/2

(4)

若rti>r2,叶片将与转轮室外环发生接触,假定不考虑摩擦热效应,并认为转轮室外环变形为线性,摩擦力采用库仑摩擦力模型,则碰摩力表达式为

(5)

式中:kr为接触刚度;f0为库仑摩擦因数;vci为接触点的相对速度。

(6)

将单个叶片的碰摩力分别投影到x、y方向有

(7)

将所有叶片的碰摩力求和,可得转轮在x、y方向所承受的碰摩力分别为

(8)

1.2 不平衡磁拉力

图4为发电机偏心转子气隙示意图。在直角坐标系O-xy内:O1(x1,y1)为转子几何形心;β为气隙宽度角度;γ为发电机转子方向角;δ1为发电机转子不偏心时的平均气隙长度。则偏心转子与定子间气隙可以近似表示为

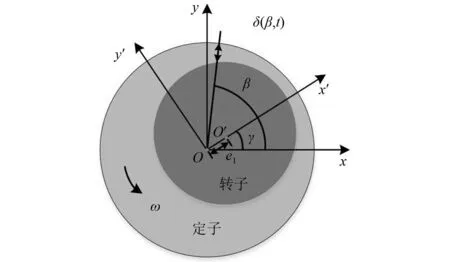
图4 发电机偏心转子气隙示意图Fig.4 Schematic diagram of air gap of generator eccentric rotor

δ(β,t)≈δ1-r1cos(β-γ)

(9)

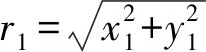
将气隙磁导展开如下级数形式

(10)

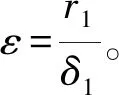
(11)

对于水轮发电机组而言,当其磁极对数P>3时,采用Maxwell应力积分方法,可得水电机组不平衡磁拉力的解析表达式[22]

(12)

式中:L1为转子长度;R1为转子半径;kj为气隙基波磁动势系数;Ij为发电机转子的励磁电流。

1.3 机组转子-转轮偏角不对中

偏角不对中转子-转轮运动坐标示意图,如图5所示。

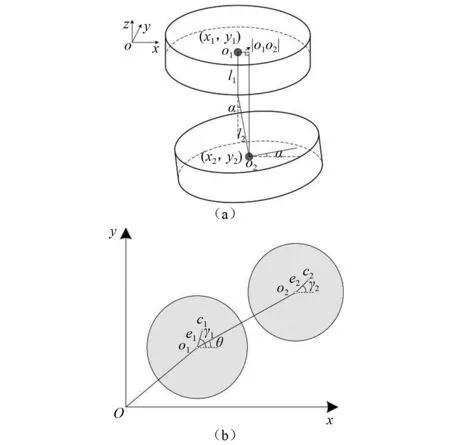
图5 系统坐标示意图Fig.5 Schematic diagram of system coordinates

(13)

式中:O1(x1,y1),O2(x2,y2)分别为发电机转子和水轮机转轮的形心坐标;θ为水轮机转轴绕发电机转轴转过的角度,θ=ωt+θ0,θ0为初相位。

由图5可知,转子、转轮的径向质心坐标分别为

(14)

(15)

式中:e1,e2分别为发电机转子的质量偏心和水轮机转轮的质量偏心;γ1,γ2分别为转子和转轮绕几何中心转过的角度,则γ1=ωt+γ10,γ2=ωt+γ20,γ10,γ20为初相位。

综合式(13)～式(15)可得水轮发电机组的总动能T和总势能U分别如式(16)和式(17)所示。

(16)

式中:T1,T2,T0分别为转子动能、转轮动能、转轮叶片总动能;J1,J2,J0分别为发电机转子、水轮机转轮与转轮叶片的转动惯量;l0为叶片质心距大轴形心的距离。

(17)

式中:U1,U2分别为转子、转轮处的弹性势能;k1,k2分别为转子、转轮处转轴刚度。

1.4 系统运动微分方程

假设发电机转子在x、y方向阻尼系数均为c,考虑碰摩力、不平衡磁拉力作用,则系统所受广义力为

(18)

式中,Px1_rub和Py1_rub表达式详见文献[22]。

令x1=x,y1=y,综合式(16)～式(18)并采用Lagrange方程推导可得机组系统运动微分方程为

(19)

2 数值分析结果

式(19)呈强非线性,本文采用4阶Runge-Kutta法对系统运动微分方程进行求解,选用积分步长为2π/200,计算1 200个周期。为消除瞬态响应影响,舍去前1 100个周期,保留最后100个周期进行分析。系统模型主要参数如表1所示。

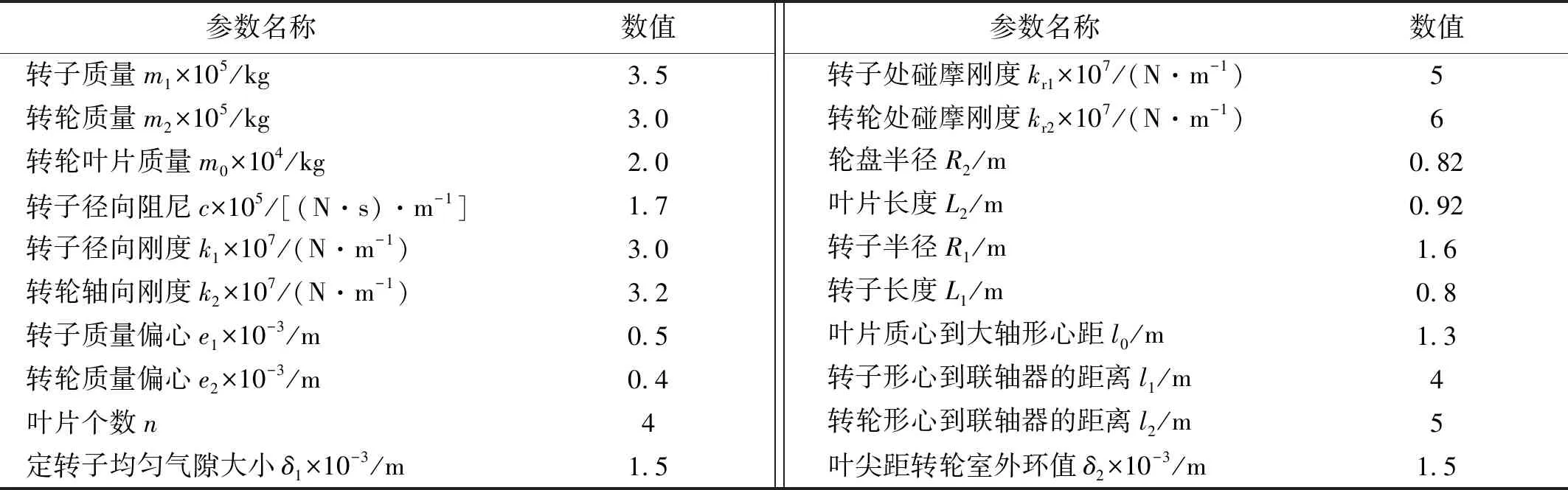
表1 转子-轴承系统模型主要参数Tab.1 Main parameters of rotor-bearing system model

2.1 转子-转轮系统周期运动稳定性分析

旋转角速度是影响机组轴系动态特性的关键参数,本节利用打靶法追踪系统周期不平衡响应,并结合Floquet理论对系统在ω=0～70 rad/s变化范围内的周期运动稳定性进行分析。

当转子-转轮系统在α=0和α=0.25×10-3rad时,系统周期解最大Floquet乘子模(|λ|max)随转速变化的关系曲线,如图6所示。当α=0及α=0.25×10-3rad时系统同频周期运动对应的最大Floquet乘子,如表2和表3所示。从图6可以看出,随着转速的增加,|λ|max多次发生明显波动,系统亦往复徘徊于稳定与失稳状态之间,Hopf分岔和鞍结分岔不断显现。

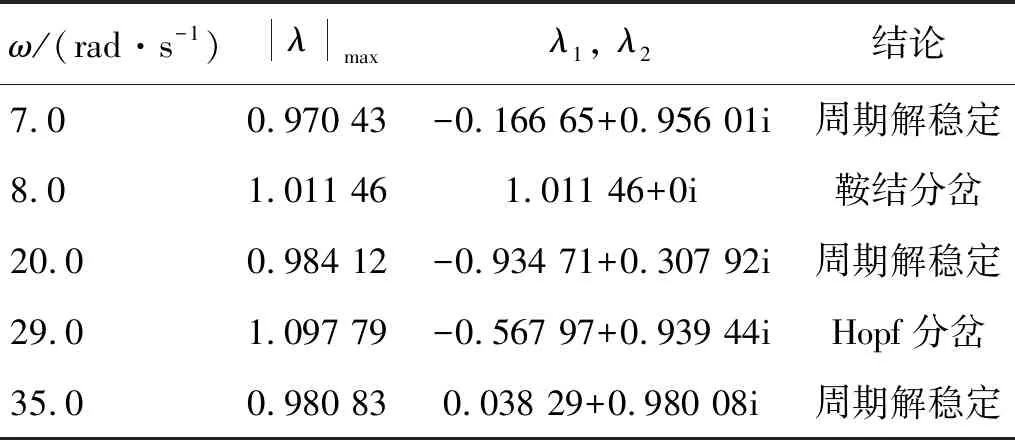
表2 当α=0时系统周期解最大Floquet乘子随ω变化情况

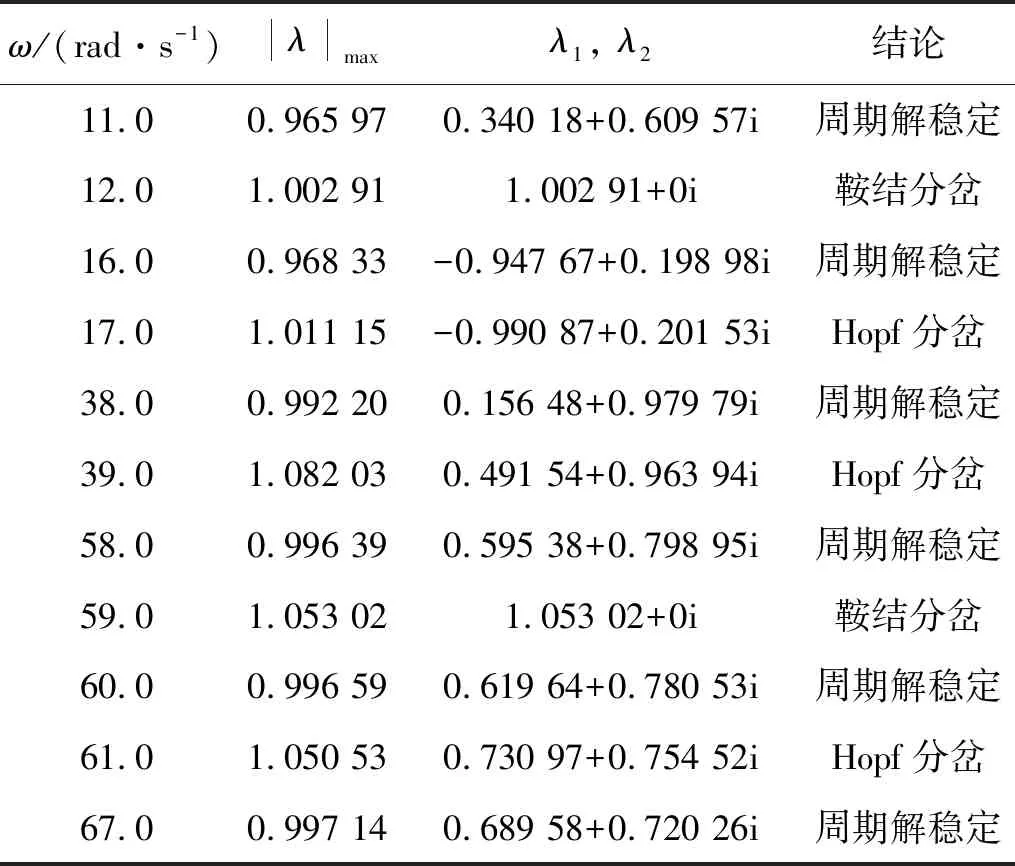
表3 当α=0.25×10-3 rad时系统周期解最大Floquet乘子随ω变化情况

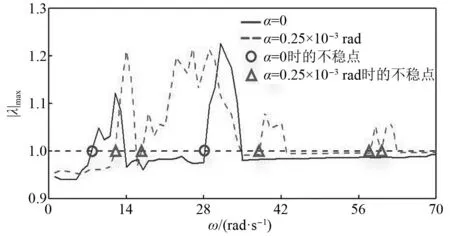
图6 系统随ω变化时|λ|max对比图Fig.6 Comparison of the system with |λ|max as ω varies

当α=0时,由图6和表2可知,在转速达到8 rad/s之前,系统周期解的最大Floquet乘子在复平面单位圆内,系统周期解处于稳定状态。当ω=8 rad/s时,系统通过鞍结分岔形式从(+1,0)方向离开单位圆,相应周期解从稳定状态直接进入非稳定状态。随着ω逐渐增大,系统最大Floquet乘子于ω=29 rad/s时由共轭复数形式穿出单位圆,Hopf分岔予以显现。

转子系统响应分岔图,如图7所示。当无不对中故障时,从图7能够发现,系统响应由周期1分岔为拟周期运动,直至转速接近35 rad/s时,系统响应重新进入稳定的周期运动。此后,伴随ω向更高转速迈进,其最大Floquet乘子一直在复平面单位圆内变动,机组在多源外激励作用下达到新的动态平衡。

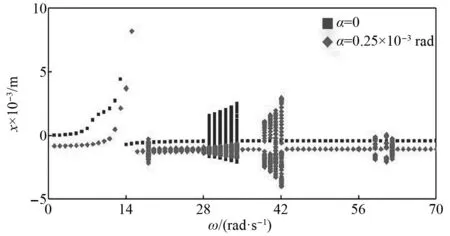
图7 以ω为控制参数是否考虑不对中角度的转子系统变化分岔图Fig.7 The bifurcation diagram of the rotor system whether considering misalignment angle or not with ω as control parameter

相比之下,加入不对中量后系统稳定性呈现以下改变:

(1) 系统失稳可能性加大,稳定运行范围显著缩减。如图6所示,当α=0.25×10-3rad时,|λ|max>1的非稳态运行范围由原先的10%上升为25%,相应散落在复平面单位圆外的最大Floquet乘子数量明显增加。此外,结合表3进一步分析可知,系统在ω=0～70 rad/s变化范围内,鞍结分岔与Hopf分岔形式交替复现,表明系统更易处于非稳态运行。

(2) 系统由稳态进入非稳态变化频次增多,失稳点增加。考虑不对中角度后,系统失稳点由ω=8.0 rad/s、ω=29.0 rad/s两处(如表2和表3所示)变为ω=12.0 rad/s、ω=17.0 rad/s、ω=39.0 rad/s、ω=59.0 rad/s、ω=61.0 rad/s等五处,不稳定变化频次大幅增加。尽管在不对中影响下,系统初始失稳点在一定程度上被延迟,但就整体而言,其稳定性呈恶化态势。

综上所述,受联轴器偏角不对中影响,系统的稳定性愈加恶化且运动形式更为多变。为进一步明确不对中角度对转子-转轮系统的作用,下面将以偏角不对中量为控制参数,讨论不对中量对转子及转轮的振动影响。

2.2 不对中量对转子及转轮径向振动的影响

当Ij=400 A、ω=40 rad/s时,发电机转子、水轮机转轮随不对中量α变化的径向振动分岔图,如图8所示。由图8可知,在α=0～3.0×10-4rad的变化区间内,两者响应变化趋势大致相似,均由周期一发展为拟周期的运动形式。其原因在于,轴流式机组为双跨结构,转子、转轮由联轴器连接形成转子-转轮轴系整体,故仅从不对中量层面考量,其改变对两者造成的动态影响是相似的。不过,转子和转轮所受外激励不同,因此两者在具体振动表现特性上有所差异。

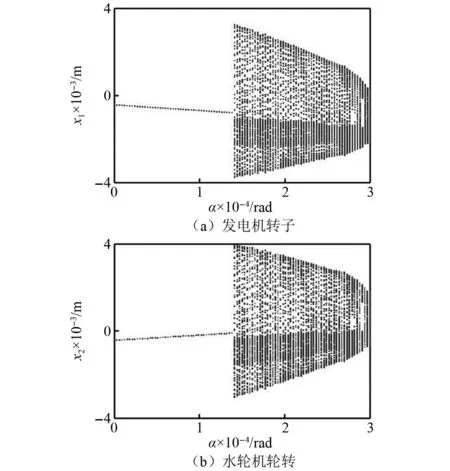
图8 转子和转轮随不对中角度α变化的径向振动分岔图Fig.8 Radial vibration bifurcation diagram of rotor and runner varying with misalignment angle α

不同不对中偏角时转子和转轮响应的轨迹图,如图9所示。由图9可知,当α=0时,系统对中情况良好,转子和转轮的动力学行为保持一致,响应均为稳定的周期一运动,如图9(a)所示。随着不对中偏角增大,两者的振动特性发生改变,通过对比图9(a)、图9(b)、图9(c)、图9(d)可以发现,在α=0～1.40×10-4rad范围内转子的振动幅值呈上升趋势,相反转轮振动则不断减小。这主要是因为α的增加致使式(19)的l2×sinα项增大,令转轮和叶片随轴系回转施加给发电机转轴的离心惯性力“(m2+nm0)l2sinαω2cosθ”和“(m2+nm0)l2sinαω2sinθ”不断增加,使得从动轴即发电机转轴的振动不断加剧,反过来又会抑制主动轴即水轮机转轴的振动,从而改变了系统的运动特性,此特点与文献[23]所述相似。

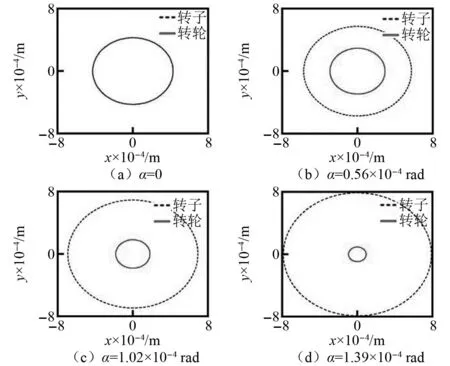
图9 不同偏角下转子和转轮响应轨迹图Fig.9 Trajectories of rotor and runner responses at different deflection angles

不同偏角下转子和转轮响应的轨迹图、映射图、时域图和频谱图,如图10所示。当α=1.41×10-4rad时,如图10(a)所示,发电机转子和水轮机转轮响应由周期运动分岔为拟周期运动,其Poincaré映射图呈现一条环形胞面点集,轴心轨迹表现为螺旋环状结构,时域图则出现了较为严重的削波和拍振现象,除1.0倍频成分外,转子与转轮于0.3倍频处产生了较为明显的低频分量,并且转子、转轮振幅均超过碰摩间隙。上述现象表明转子与定子、转轮叶片与转轮室均发生了碰摩。相比之下,转轮的低频分量更为显著,轴心轨迹外环边缘更加尖锐,说明转轮的碰摩程度相较转子更为强烈。随着不对中偏角持续增大,转子、转轮的动力特性也在不断变化,如图10(b)所示,可以发现由于外激励影响下偏角不对中和碰摩的耦合作用,转子和转轮的振动幅值减小,时域波形走势平缓,其拟周期特征出现减弱趋势。

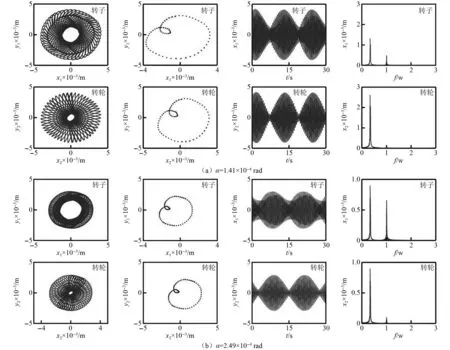
图10 不同偏角下转子和转轮响应的轨迹图、映射图、时域图和频谱图Fig.10 Trajectories, poincaré maps, time domains and frequency spectrums of rotor and runner response under different deflection angles

综上所述,不对中量虽较小,但在恶化系统运动方面却具有明显作用。究其原因,根据式(1)及式(5)可知,不对中角度的存在令转轮叶片与转轮室碰摩间隙B减小,导致转轮部分动静件发生碰摩的概率增大,故由此形成的外激励加剧了转子-转轮系统振动。

3 结 论

针对轴流式水轮发电机组因联轴器偏角不对中引起的转子、转轮碰摩问题,本文建立了机组轴系动力学模型及其运动微分方程,采用数值仿真方法对系统运行稳定性及动态响应进行了分析,主要结论如下:

(1) 随着转速变化,机组轴系响应存在周期、拟周期等运动现象,是否考虑不对中角度系统动态特性呈明显差异。不对中存在令系统失稳概率增大,导致稳态与非稳态响应的交替频率增加,严重影响系统安全稳定运行。

(2) 不对中故障对转子及转轮振动影响存在明显差异。相较于转子,不对中角度对转轮振动影响更为显著,且随不对中偏角增大,转轮碰摩程度愈发恶劣。

总体而言,综合考虑机组轴系不对中及转轮叶片碰摩力作用,可更为全面地揭示系统在复杂激励影响下的整体动态特性,故在建模时应对此给予足够重视。