诱导轮对高速液氧泵空化流场影响研究

窦 唯, 蒋文山, 李超群, 高永新, 姚 程

(1. 北京航天动力研究所,北京 100076; 2. 合肥工业大学 土木与水利工程学院,合肥 230009)

高可靠性大推力液体火箭是支撑我国开展太空探索的重要装备。高速液氧泵是液体火箭发动机的重要组成部分,其主要功能是为火箭发动机实现液氧的输运与增压。离心轮是高速液氧泵的核心构件,在其高速旋转时会出现空化现象[1]。空化过程是一种复杂的流体力学现象,是离心泵稳定和可靠运行的关键因素之一[2-3]。当液氧泵离心轮在高速旋转时,轮缘处绝对速度较大,使得离心轮前缘静压降低;当静压低于液氧的饱和蒸汽压时,会在叶片表面的低压区发生汽化,从而在叶片表面和流道中产生细小的气泡,并呈现增长趋势;当气泡经过高压区域时,会发生溃灭;气泡溃灭后,液氧快速填充空穴,互相撞击,引起叶片汽蚀。空化现象不仅损伤离心轮叶片,还会削弱液氧泵吸入性能,甚至影响发动机转子动力学特性。一般采用前置诱导轮抑制液氧泵离心轮空化,提高液氧泵的吸入性能[4]。

国内外学者对空化现象开展了大量的试验研究。李欣等[5]探究了三叶片两级诱导轮的汽蚀性能,发现两级诱导轮相较于一级诱导轮,叶尖间隙大,增强了回流,改善了诱导轮的汽蚀性能,同时降低了旋转汽蚀的强度。黄建德等[6-7]分析了两叶片诱导轮汽蚀导致扬程和效率下降的机理。Bramanti[8]研究了涡轮泵的诱导轮和离心轮的汽蚀现象,对不同工况和不同型线的诱导轮和离心轮进行了压力脉动测量和汽蚀现象观察,得到了涡轮泵的汽蚀特性。Coutier-Delgosha等[9]探究了诱导轮叶片数对诱导轮的空化性能影响,对比了三叶片诱导轮和五叶片诱导轮试验。结果表明,两种诱导轮均出现叶尖空化,与传统四叶片诱导轮的片状空化不同;当压力下降时,三叶片诱导轮更易发生性能崩溃。

近年来,数值模拟方法被广泛用于液氧泵空化现象的研究。Kimura等[10]对涡轮泵诱导轮内部的非定常空化流动进行了数值仿真,认为间隙涡和叶片之间的交互作用与旋转空化有着很大的联系。李龙贤[11]采用数值计算和可视化试验手段研究了低温火箭发动机诱导轮内部的空化过程,表明数值计算结果和可视化试验结果吻合良好,证明了数值方法对诱导轮空化流场计算的可行性。司乔瑞等[12]对带诱导轮的高速离心泵的内部流场进行了三维非定常数值计算,并分析了带诱导轮的高速离心泵的振动特性。结果表明,诱导轮顶部的振动位移呈周期性变化,且垂直方向大于水平方向。上述研究中多采用二叶片或三叶片诱导轮作为研究对象,证明了前置诱导轮抑制离心轮空化的有效性。在高可靠性大推力液体火箭的研究中,二叶片或三叶片诱导轮对液氧泵的影响鲜有公开报道。

本文以某大推力液体火箭发动机的高速液氧泵为研究对象,通过改变诱导轮的叶片数目,量化了不同诱导轮叶片数的液氧泵内部流场及空化特性,探究了诱导轮叶片数对液氧泵性能参数和空化特性的影响。

1 数值方法

1.1 控制方程

为了描述液氧泵内部的空化过程,本文采用多相流模型,将流体中的各相看作相互混合的单一流体。计算采用基于Rayleigh-Plesset气泡动力学模型推导出的Schnerr-Sauer空化模型。模型的基本相为液态氧,第二相为气态氧。液态氧的密度为1 142 kg/m3。动力黏度系数为1.958 2×10-4Pa·s。气态氧的密度为1.225 kg/m3,动力黏度系数为1.789 4×10-5Pa·s。通过求解流体混合物的连续性方程和动量方程来模拟液氧泵内的两相运动。

连续性方程如式(1)和式(2)所示

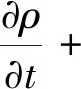
(1)

ρ=αlρl+αvρv

(2)

式中:V为速度矢量;ρ为气液两相流体密度;αv为气态氧的体积分数;αl为液态氧的体积分数;ρv为气态氧密度;ρl为液态氧密度。

动量方程如式(3)所示

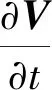
(3)

式中:f为作用在单位质量上的体积力;μ为流体的动力黏性系数;p为流场压力;ψ为体积力牵引的动量方程源项。

本文采用Schnerr-Sauer空化模型[13],如式(4)所示。该模型假设液体区域内均为球形气泡,且气泡间无相互作用。

式中,pv为液氧的临界饱和蒸汽压力,值为130 480 Pa;p∞为远场压力;σ为液体表面张力系数;μl为液态氧的动力黏度系数。

Schnerr-Sauer空化模型采用气泡数密度及气泡半径定义气相体积分数,但不考虑非冷凝气体及湍流脉动对空化流的影响,即

(5)

(6)

(7)

式中:Rb为气泡半径;Re和Rc分别为气泡产生和气泡溃灭的质量输运源项。ξ=1×1011为气泡数密度。

液氧泵的扬程H如式(8)所示[14]

(8)

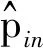
液氧泵的效率为有效功率与输入功率的比值,如式(9)所示[14]

(9)

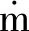
1.2 几何模型和边界条件

本文以带诱导轮的高速液氧泵为研究对象,主要用于某型大推力液体火箭发动机。液氧泵由进口管、诱导轮、导流支座、离心轮、涡壳和出口管组成,如图1所示。入口直径为143.5 mm,出口直径为70 mm。诱导轮采用多叶片变螺距设计,诱导轮直径为142 mm,叶片轴向跨度为70 mm。

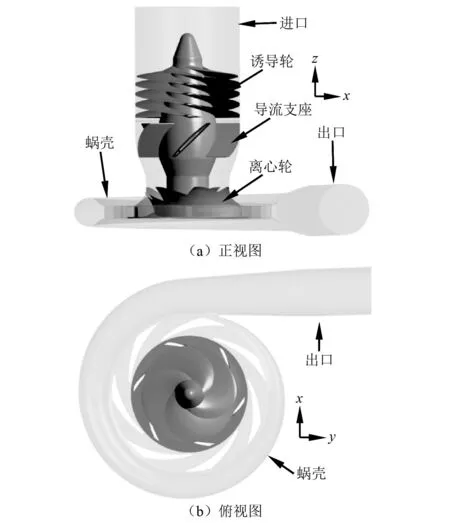
图1 液氧泵几何模型Fig.1 Geometry of a liquid-oxygen-pump

液氧泵入口采用流量入口边界条件。液氧泵出口采用压力出口边界条件。各固体壁面均采用无滑移壁面边界条件。其中,诱导轮外壳、诱导轮轮毂、诱导轮叶片、离心轮前后盖板和离心轮叶片设置为旋转壁面,其他固体壁面都设置为静止壁面。

2 网格无关性及试验验证

为了提高数值计算的收敛性,将入口延伸500 mm(约为入口直径的3.5倍),出口延伸500 mm(约为出口直径的7倍)。复杂几何结构区采用非结构化四面体网格。进口管和出口管延长段采用六面体网格。网格无关性验证采用五种不同的网格划分方案,如表1所示。液氧泵的扬程H随网格节点数β的变化曲线如图2所示。可以看出,网格Ⅳ的扬程H与精细化网格Ⅴ更为接近。因此,采用网格Ⅳ方案对液氧泵流域进行网格划分,无诱导轮的液氧泵流场总网格节点数约为1 638万。

表1 网格划分方案Tab.1 Mesh schemes

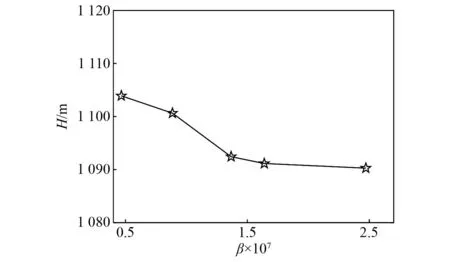
图2 扬程随网格节点数变化曲线Fig.2 Variation of pumping head with mesh grids

为了验证本文数值模型的准确性,分析了三种工况时的液氧泵性能参数,并与试验结果进行对比。试验对象采用带三叶片诱导轮的高速液氧泵。通过调整入口流量,改变液氧泵工况,获取不同工况下液氧泵的扬程和效率。图3分别展示了三种工况下液氧泵扬程和效率随入口流量的变化曲线。其中,工况二为标准工况。可以看出,随着入口流量的增大,液氧泵的扬程逐渐上升,效率略有下降。

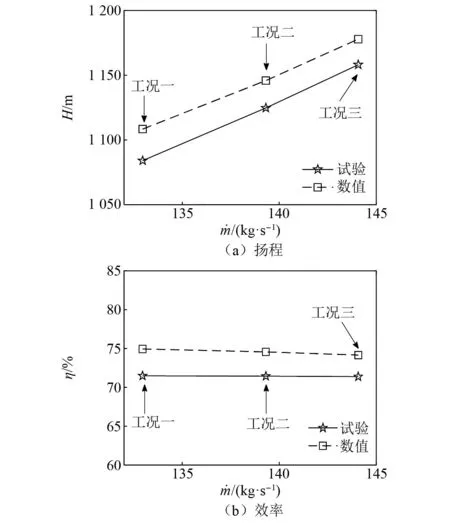
图3 三种工况时的性能参数Fig.3 Performance parameters under three test conditions

图3所示的数值结果中,扬程和效率随流量变化的规律和趋势与试验规律一致。数值模拟所得的液氧泵扬程和效率均略高于试验值。液氧泵的扬程和效率的最大相对误差均发生在工况一,分别为2.2%和4.8%。因此,本文采用的数值方法可以满足液氧泵流动计算的要求。

3 结果与分析

空化现象会损伤液氧泵诱导轮和离心轮的叶片。本节重点讨论诱导轮叶片数对液氧泵的性能参数(扬程和效率)和空化特性的影响。

3.1 无诱导轮液氧泵流场分析

液氧泵的流场分析能够直观地反映液氧的输运和增压过程。首先基于工况二对无诱导轮的液氧泵流场进行数值模拟,为后续讨论诱导轮叶片数的影响提供对照。此时,液氧泵的扬程为1 090 m,效率为76%。

图4为无诱导轮液氧泵外壁面压力分布。可以看出,从液氧泵的进口管至离心轮进口段,壁面压力p1沿流向持续降低至p2。离心轮进口位置直径小于液氧泵进口段,导致流速增加,壁面压力减小。随后,从离心轮到出口管,壁面压力从p2逐渐增加至p3。液氧泵最大压力出现在蜗壳表面,其值为13.82 MPa。

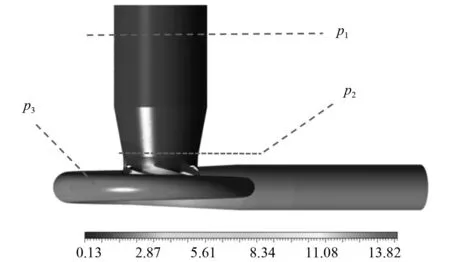
图4 液氧泵外壁面压力分布(MPa)Fig.4 Pressure distribution on the outer wall of pump

当离心轮叶尖处局部静压降低到液氧饱和蒸汽压时,液氧发生沸腾、汽化,形成气泡。气泡和液氧在离心轮作用下向蜗壳移动。当气泡到达高压区域时,气泡发生溃灭。此时,液氧会以极高速度占据气泡空间,并对该局部区域离心轮叶片产生冲击,形成汽蚀现象。

为了量化液氧泵内部不同部件空化过程的强弱,本文分别定义了离心轮和诱导轮叶片空化面积比,如式(10)和(11)所示

(10)

(11)

式中:φc和φi分别为离心轮和诱导轮叶片表面的空化区域面积比;S1为离心轮表面空化区域面积;Sc=37 282.7 mm2为离心轮叶片面积;S2为诱导轮单叶片表面空化区域面积;Si=31 027.8 mm2为诱导轮单叶片面积。

图5为无诱导轮液氧泵的离心轮叶片表面空化区分布。可以看出,空化区域主要分布在离心轮叶片前缘,各叶片表面均呈现较大的空化区域。离心轮表面的空化区域面积S1=9 245.57 mm2。离心轮叶片空化面积比φc=24.8%。

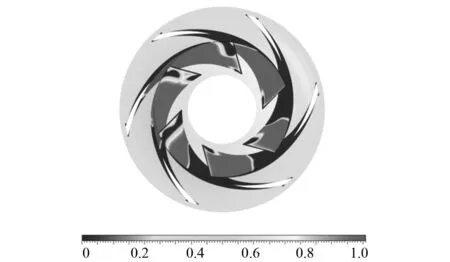
图5 无诱导轮时离心轮叶片表面空化区分布Fig.5 Cavitation on the centrifugal wheel blades without inducer

图6和图7分别为液氧泵离心轮和蜗壳区域压力分布。可以看出,离心轮叶片表面的低压区域与图5所示的离心轮叶片表面的空化区域相互对应。离心轮区域的压力自离心轮中心向蜗壳方向逐渐增加,在蜗壳表面达到最大压力13.82 MPa。液氧随着离心轮的高速旋转,在离心力的作用下自离心轮中心被甩向蜗壳区域,实现液氧的快速增压。蜗壳内流道直径随流向逐渐增大,液氧流速逐渐降低,动能转换为压力势能,高压强的液氧流向出口管。因此,最大壁面压力出现在蜗壳表面。

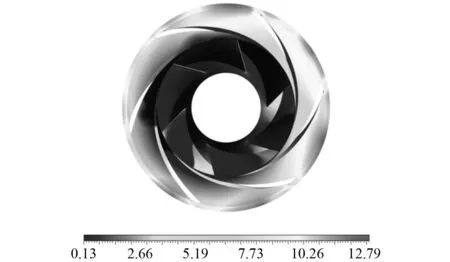
图6 无诱导轮时离心轮压力分布(MPa)Fig.6 Pressure on the centrifugal wheel blades without inducer

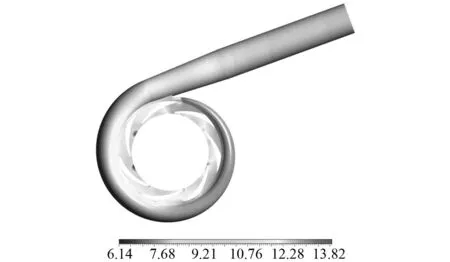
图7 无诱导轮时蜗壳压力分布(MPa)Fig.7 Pressure on the worm housing without inducer

3.2 诱导轮叶片数对液氧泵的影响

为了探究诱导轮叶片数对液氧泵性能和空化特性的影响,本文基于工况二对四组不同叶片数诱导轮及其液氧泵的流场进行数值模拟。单叶片诱导轮会导致泵体的不稳定,因此本文未考虑单叶片诱导轮。当诱导轮叶片少于离心轮叶片,且与离心轮叶片呈倍数关系时,泵内部呈现较好的流动对称性。因此,诱导轮叶片数一般不大于离心轮叶片数。本文采用6叶片离心轮,故本节中诱导轮叶片数n分别取为2、3、4和5。

液氧泵内部空化区的分布与流场的压力分布密切相关。图8和图9分别为诱导轮叶片表面的压力分布和空化区分布。在图8中,黑色区域表示低于液氧饱和蒸汽压的区域,灰色为高压区域;在图9中,灰色区域为空化区域,黑色为未发生空化区域。可以看出,诱导轮叶片表面的低压区域和空化区域相互对应。

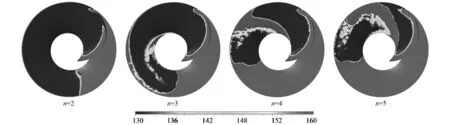
图8 诱导轮表面压力分布图(kPa)Fig.8 Pressure on the inducer

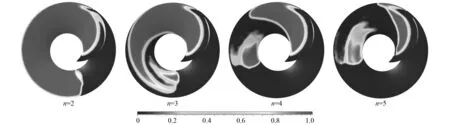
图9 诱导轮表面空化区分布图Fig.9 Cavitation on the inducer

随着诱导轮叶片数目的增加,诱导轮叶片表面的低压区域逐渐减小,空化区域的面积也随之下降,空化现象被有效抑制。n=2时,诱导轮单叶片表面的空化区域面积S2=11 133.9 mm2;n=3时,空化区域面积S2=8 395.1 mm2;n=4时,空化区域面积S2=5 394.9 mm2;n=5时,空化区域面积S2=1 457.6 mm2。

图10和图11分别为离心轮叶片表面低压区和空化区的分布图。无诱导轮时,离心轮表面的空化区域面积S1=9 245.6 mm2,如图5所示。当采用前置诱导轮时,离心轮叶片表面空化区域急剧减小,有效抑制了离心轮的空化。其中,n=2时,离心轮表面的空化区域面积S1=3.9 mm2。由此可以看出,前置诱导轮有效代偿了离心轮叶片表面的汽蚀。

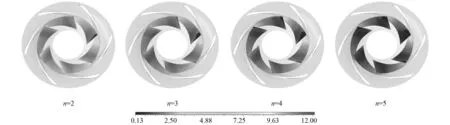
图10 离心轮表面压力分布图(MPa)Fig.10 Pressure on the centrifugal wheel

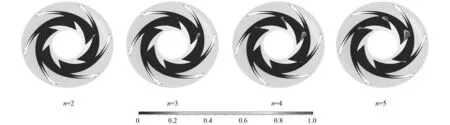
图11 离心轮表面空化区分布图Fig.11 Cavitation on the centrifugal wheel

另一方面,随着诱导轮叶片数目的增加,离心轮叶片前缘的低压区逐渐增大,空化区的面积逐渐增加。其中,n=3时,离心轮表面的空化区域面积S1=25.7 mm2;n=4时,离心轮表面的空化区域面积S1=96.5 mm2;n=5时,离心轮表面的空化区域面积S1=218.9 mm2。因此,诱导轮代偿离心轮汽蚀的效果随着其叶片数目的增加而降低。

图12汇总了诱导轮和离心轮空化面积比随叶片数目的变化关系。可以看出,在入口流量和出口压力不变的条件下,随着诱导轮叶片数的增加,诱导轮表面的空化区降低,离心轮表面的空化区增加,诱导轮代偿离心轮叶片表面汽蚀的效果削弱。其中,n由2增加到3时,离心轮空化面积比φc略微增加,诱导轮空化面积比φi显著降低。当n增加到4时,φc显著增加。在抑制离心轮叶片空化特性时,3叶片诱导轮较2叶片和4叶片更合理。

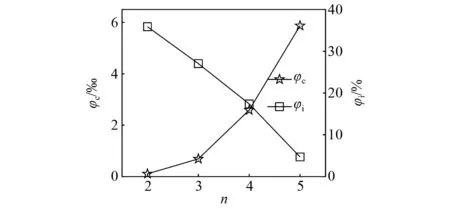
图12 诱导轮和离心轮空化面积比随叶片数变化曲线Fig.12 Cavitation areas variation with inducer-blade number

另一方面,还需要关注诱导轮叶片数对液氧泵性能参数的影响。图13为液氧泵的扬程和效率随诱导轮叶片数目变化曲线。可见,液氧泵的扬程随着叶片数增加而降低,而液氧泵的效率随叶片数增加而升高。采用3叶片或4叶片诱导轮的液氧泵性能参数更合理。

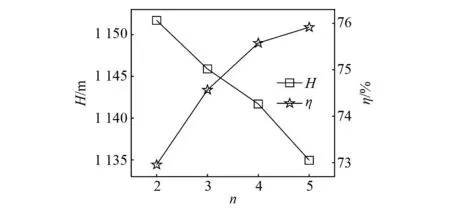
图13 泵扬程和效率随叶片数目变化曲线Fig.13 Head and efficiency variation with inducer-blade number

前述研究中一般采用2叶片或3叶片诱导轮抑制液氧泵离心轮的空化过程。结合图12和图13可以看出,本文研究的高速液氧泵采用3叶片诱导轮比2叶片诱导轮更适合大推力液体火箭可靠运行。

4 结 论

本文采用计算流体力学方法和Schnerr-Sauer空化模型,分析了诱导轮叶片数对某大推力液体火箭发动机液氧泵性能参数和空化特性的影响,得到如下结论:

(1)无诱导轮的液氧泵在高速旋转时,离心轮叶片前缘出现大面积空化,严重影响泵的性能。采用前置诱导轮可以有效代偿液氧泵离心轮上的汽蚀。

(2)在入口流量和出口压力不变的条件下,随着诱导轮叶片数目由2增加至5,诱导轮代偿离心轮叶片上汽蚀现象的能力逐渐削弱。

(3)综合考虑诱导轮代偿能力和液氧泵性能参数,三叶片诱导轮可以满足大推力液体火箭可靠运行的要求。