动车组头车声固耦合模态分析及多目标优化

于 洋, 曹启军, 刘春艳, 陈秉智, 于春洋

(1. 中车长春轨道客车股份有限公司,长春 130021; 2.大连交通大学 机车车辆工程学院,辽宁 大连 116028)

高速动车组车体结构的固有振动特性是结构设计中考虑动态载荷影响的重要参数。模态分析旨在提取结构固有频率和振型,为动力学分析和动态设计奠定基础。通过对车体结构进行模态分析,可评定其动态特性能否满足设计要求,确保列车具有良好的乘车舒适性,并为后续动力学优化设计提供依据。

为全面分析车体结构的动态特性,除了分析结构的固有振动特性,还需要进一步考虑声场对结构的反馈作用,即声固耦合因素的影响。目前,高速列车本征动力学特性研究主要集中在结构固有频率及模态振型分析[1-5],关于声场模态测试及声-结构耦合模态分析研究有待于深入开展。文献[6-8]中的高速列车声学模态分析仅涉及内声场,未考虑结构与声场的耦合效应。杨志康[9]以中间车为研究对象,分析了考虑耦合作用下的结构动态特性和车内声压变化。徐凯等[10]建立CRH 5型动车组车厢声固耦合有限元模型,综合比较结构模态、声场模态和声固耦合模态的振型特点,发现引入耦合因素影响的系统振型与非耦合结构模态相对应,声场对耦合系统模态影响较小。刘太祥等[11-12]也建立了动车组声固耦合有限元模型,分析耦合状态下的车体结构固有振型及内声场声压分布特征。上述研究仅考虑结构与内部声场的耦合,未综合考虑外部声学介质对系统动力学特性的影响;此外,相关工作仅停留在耦合因素对系统声振特性影响的描述性分析阶段,并未针对避免该耦合共振现象进行优化设计。

轻量化设计是高速列车结构优化理论的重要组成部分。近年来,在保证车体结构固有振动指标可靠的前提下进行轻量化研究受到广泛关注[13-14]。现有研究仅将车体结构的一阶垂弯频率纳入优化模型的约束条件,并未充分考虑声固耦合共振对车体结构振动响应的影响。对于声振耦合系统共振影响因素的理论研究已有不少成果,如Pan[15]基于模态耦合分析法研究了简支板和矩形声腔构成耦合系统的模态特性,分析了简支板厚度、阻尼等因素对耦合系统特性的影响。王园等[16]在文献[15]的基础上,进一步分析了声腔深度变化对板-声腔系统耦合动力学特性的影响,其研究对象仍为简支板与矩形声腔组成的简单系统,未涉及复杂结构与声腔之间的耦合问题。以能量为基本变量的统计能量分析方法是研究复杂系统结构和声场的相互作用的有效方法,也是中高频声振动力学分析的主流手段。该方法将研究对象划分为若干个子系统,建立稳态振动状态下各子系统之间的能量流平衡方程[17]。Louisell[18]在研究线性耦合振荡器运动方程时引入传递因子概念以衡量不同振子模态间能量传递程度,发现当两个非耦合振子模态频率相同时能量完全传递。Lyon[19]假定弱线性耦合,计算了随机载荷激励下两个谐波振荡器之间的功率流,发现功率流与两个振荡器平均模态能量差成正比,当耦合系数中声场与结构固有频率相等时模态间能量传递效率最高。针对以上研究可见,为减弱高速列车耦合共振作用,降低模态之间的能量传递,需要避免车体结构及声场有接近的模态频率。

当声腔与结构子系统的固有频率接近时,会产生声固耦合共振现象,造成结构子系统振动幅度增大、声腔内声压升高,从而加剧结构的疲劳破坏和失效风险,产生噪声污染和听力损害。朱凯等[20]以某拖拉机驾驶室为研究对象建立声固耦合模型并进行模态分析,发现驾驶室内声压作用引起结构振动频率发生一定变化;龚京风等[21]利用声固耦合数值模型分析不同部位的耦合效应对充水膨胀腔消声器声学性能的影响,发现周向腔壁的耦合效应导致传递损失曲线向低频偏移,膨胀腔壁的耦合作用引起传递损失曲线出现明显峰值;艾延廷等[22]分析燃烧室封闭结构的声振耦合特性,发现声场的反馈作用相当于增加了结构的附加质量,使结构固有频率下降,并且得出了耦合频率的具体数值;张义波[23]在商用车驾驶室的结构噪声分析研究中发现,在两种特定工况下166 Hz附近车身结构与声腔发生耦合共振,作者通过形貌优化提高结构固有频率以增加结构和声腔的固有频率间隔,消除了共振影响,降低最大峰值声压。由此可知,调节声场及结构固有频率以避免声固耦合共振现象具有较高理论价值及工程意义。

本文从有限元法、统计能量法两方面阐述高速列车声固耦合共振影响因素的理论基础;基于模态等效和质量等效原则对高速列车头车结构进行有限元建模,分别提取结构模态、声场模态及考虑内外声场作用的声固耦合模态;基于结构模态提取结果进行减重优化,实现满足车体动态特性要求的最佳质量分布;为消除耦合共振影响、提高车厢舒适度,在车体减重设计模型基础上引入声-结构耦合共振关键参数,建立舒适性与轻量化同步提升的多目标优化体系。

1 声固耦合共振理论

1.1 有限元理论中的共振影响因素

有限元模态分析将动力学方程组中的物理坐标转换成模态坐标以实现方程组的解耦,从而得到系统的模态参数。针对高速列车头车声固耦合系统,建立有限元模型并将其离散成有限个自由度,当结构表面和内部声场受到简谐激励时,该耦合系统离散形式的结构和声场动力学方程分别为[24]

(Ks+jωDs-ω2Ms)U=Fs+Fa

(1)

(Ka+jωDa-ω2Ma)P=-ω2RU

(2)

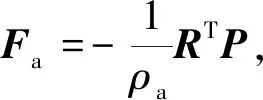
式(1),式(2)可通过模态法求解,利用模态分析计算出式(1),式(2)的互异特征值和相应的特征向量,从而将式(1),式(2)中的位移和声压响应向量由物理坐标系转换为模态坐标系[25]

U=Ψη
P=Φξ

(3)

式中:Ψ和Φ分别为解耦的弹性边界结构模态矩阵和刚性壁声场模态矩阵;η和ξ分别为对应的结构和声场模态坐标向量。

式(1)中,与结构激励Fs的作用相比,声压变化对结构边界运动的影响非常小,因此可将声压载荷Fa忽略。假定结构系统与声场系统的阻尼均为比例阻尼,将式(3)代入式(1),式(2)中,并且分别左乘结构和声场的模态转置矩阵ΨT、ΦT,可得模态坐标系下的动力学方程

(4)

式中:I为单位矩阵;c为结构模态与声场模态之间的耦合矩阵,矩阵内的元素为

(6)

η可由式(4)直接表示,将其代入式(5)中,推导出声压P的表达式为

(7)

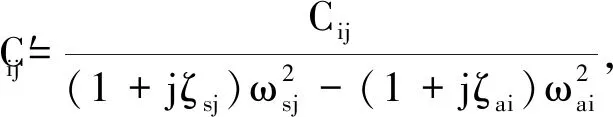
在阻尼很小的情况下,忽略结构与声场的阻尼因子ζsj与ζai,声压P近似为

(8)

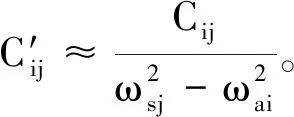
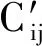
1.2 统计能量分析中的共振影响因素

有限元法将系统离散成有限个单元,建立由单元节点构成的动力学微分方程。该方法主要适用于中低频域的系统动力学问题,在结构动力学特性分析时只能考虑有限数量的低阶模态,并且随着频域和结构复杂度的增加,分析误差和难度相应增大,导致难以确定复杂系统的高阶模态参数[26]。相比之下,统计能量方法将系统划分为N个共振子系统,并假设各子系统之间相互独立且能够存储振动能量。该方法通过计算子系统之间的功率流和功率流平衡方程以获得各子系统能量储存和传递情况,从而反映子系统振动状态,适合解决高频区内复杂系统动力学问题[27]。

统计能量分析基本方程为功率流平衡方程,稳态振动时,在子系统激励相互独立及保守弱耦合(耦合损耗因子明显小于内损耗因子)情况下,各子系统线性功率流平衡方程可表示为

(9)

式中:Πi,in为外界对子系统i的输入功率;Πi,diss为子系统i的阻尼损耗功率;Πij为子系统i传递到子系统j的功率(双向),可写为[28]

Πij=βij(Ei-Ej)

(10)

式中:

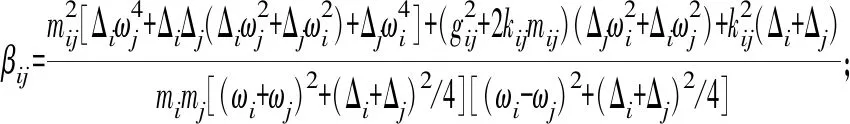
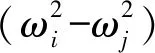
本节从有限元理论、统计能量理论两个角度分析耦合共振影响因素,发现在中低频域和高频区间内的系统动力学问题中,当非耦合结构和声场系统模态频率接近时会导致系统间能量传递显著,表现为声腔内部声压急剧升高、结构表面剧烈振动。因此,为减弱或避免动车组头车结构与声场发生耦合共振、提高车厢舒适性,需要避免结构与声场模态频率接近。

2 非耦合状态下头车模态分析

2.1 模态等效以及质量等效原则

动车组头车地板、侧墙、顶板、端墙等部位均为铝合金中空型材结构,由内外蒙皮和中间的加强筋构成。若以传统实体单元进行有限元建模,需要在狭小筋板处设置较高精度的网格,并且需要大量三维单元划分中空型材封闭的声场空间,这将限制模态提取速度和结构优化效率,同时对计算机硬件条件要求过高。为克服上述问题,基于模态等效原则[29],采用文献[30]中等效建模方法,保持中空型材的内外蒙皮参数不变,将中间的加强筋及空气等效为虚拟材料,形成等效NVH三层板,使等效板与原型材结构动态特性误差控制在10%以内,等效前后结构整体的几何尺寸、密度相同。中空型材的模态等效示意图如图1所示。

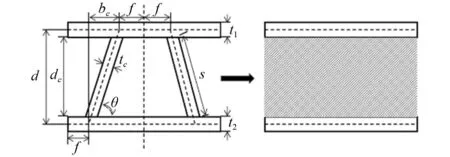
图1 中空型材模态等效示意图Fig.1 Schematic diagram of the hollow profile based on the modal equivalence

基于等质量原则应用中空型材结构的等效密度方法修正等效板的材料密度参数[31],假定铝合金型材的密度为ρ,该型材结构中间层的等效密度ρe为

(11)

根据以上两种等效方法,可将头车中空型材结构等效为NVH三层板,具体的材料属性参数如表1所示。

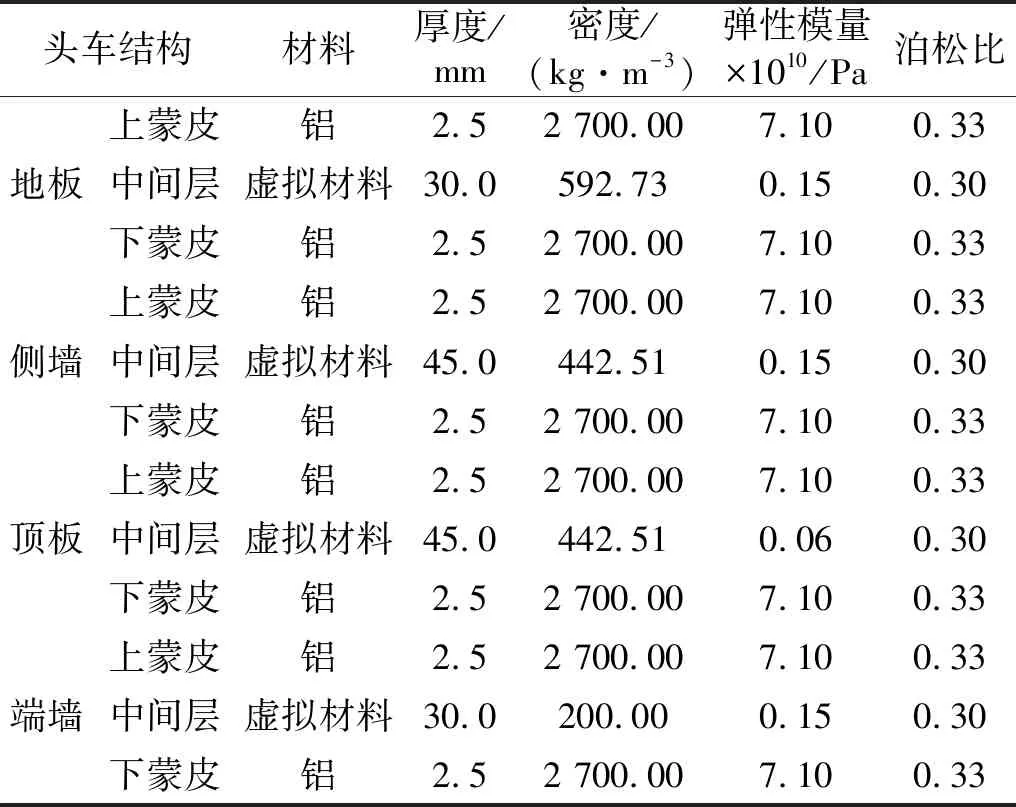
表1 等效结构材料属性Tab.1 Properties of equivalent structural materials

通过有限元软件COMSOL对几何模型进行网格划分,车身结构和车内声场分别采用壳单元及四面体域网格离散。考虑到20 Hz是人耳能感受到的最低频率,且低频噪声主要源于200 Hz以下的车身结构振动,因此模态分析的频率区间选取20～200 Hz。依据相关网格尺寸标准,声腔网格最大单元的边长不超过最高计算频率200 Hz处波长的1/6。整车共划分30 752个三角形壳结构单元,251 657个四面体声腔单元,且车体各部分的板厚按照实际参数定义为实常数,车体有限元离散模型如图2所示。

图2 车体有限元模型Fig.2 EMU finite element model

2.2 结构模态分析结果

结构模态分析采用无约束自由边界条件,前6阶模态主要为车身相对于转向架的低频刚体振动位移,即刚体模态,不予考虑。表2为忽略刚体模态的前6阶及第12阶模态固有频率及振型描述,发现不同阶次结构模态的相对变形位置不同,且随着阶数增加,模态振型更加复杂。车体1阶垂向弯曲模态出现在第5阶,其固有频率为19.314 Hz。根据文献[32],整备车体的弯曲振动频率总体降低约20%,因此该动车组头车整备状态下的弯曲振动频率约为15.45 Hz,满足《200 km/h 及以上速度级铁道车辆强度设计及试验鉴定暂行规定》标准[33]中的要求:“车体整备状态下最低弯曲振动频率大于10 Hz”。

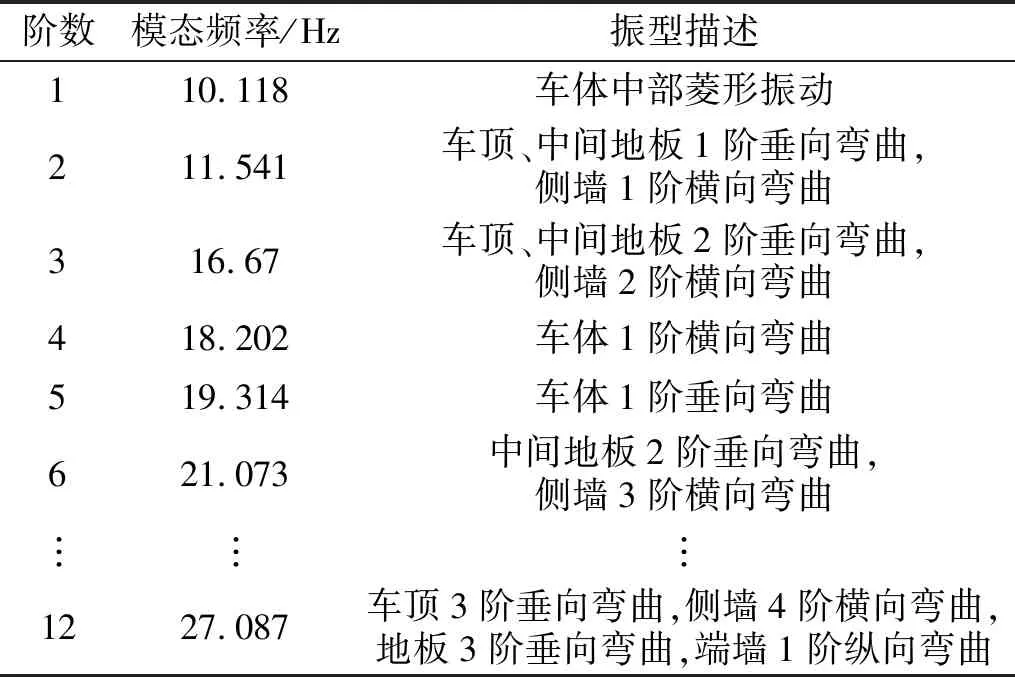
表2 头车结构模态Tab.2 Structural modes of head car

2.3 声场模态分析结果

声场模态频率是声腔内部声音的共鸣频率,在各阶模态频率附近,车室内的空腔会产生声学共振,导致声压急剧升高。对头车室内空腔声学模态进行分析可确定是否存在共振现象,为车内声学结构设计提供依据。计算前20阶室内空腔声学模态,其中第1阶模态频率为0,表示车室内各点声压变化的幅值相同,类似于结构模态中的刚体模态,忽略不计。表3为忽略一致声压的前6阶声场模态固有频率及振型描述,发现低阶均为纵向声学模态,声压沿纵向分布,模态振型随着频率的增加而复杂;表中的第四阶声场模态频率(27.335 Hz)与第12阶结构模态频率(27.087 Hz)十分接近,根据耦合共振影响因素理论,在该频率附近车内声腔与车身结构发生耦合共振的概率显著提高,从而加剧室内噪声,影响旅客乘车舒适性[34]。因此,针对该耦合共振问题,有必要进行相关的优化设计使结构和声场模态频率错开。

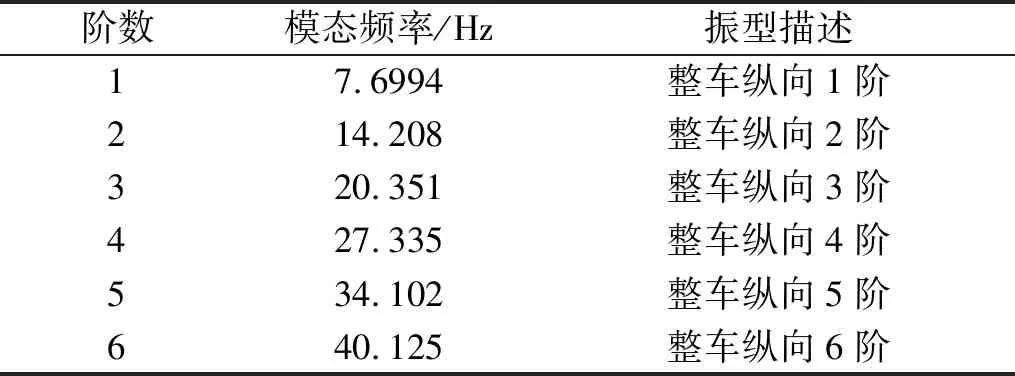
表3 头车声场模态Tab.3 Acoustic modes of head car

3 考虑内、外声场影响的头车声固耦合模态分析

为确保运行时高速列车的结构稳定性和乘坐舒适度,需要分析声场耦合作用下头车结构的固有振动特性。传统的声固耦合分析方法仅考虑内声场影响,忽略了外声场作用。然而,高速列车在运行过程中会受到复杂的气动载荷,导致头车表面结构产生振动和声辐射。这些声辐射不仅造成沿线噪声污染,还会通过结构传递和空气透过等方式进入车厢内部空间,影响车身结构的振动幅度及乘客的听觉感受。因此,在头车设计过程中,需要综合考虑内声场、外声场和头车结构之间的模态耦合效应,以评估头车结构动力学特性,为其几何形状和参数优化提供依据。

对于两侧均带有声学介质的壳结构,由于厚度较小,结构上下表面之间的压力分布有所不同,可通过在压力变量上引入切口实现该压力的不连续性,相当于在结构中间添加界面使其上下表面分离,并确保上下表面能够连接起来。该结构-内、外声场耦合边界条件为

(12)

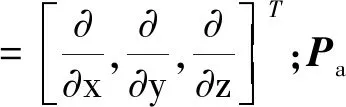
为模拟声波在外声场传播的无限性,构建头车结构有限元模型的外声场时,需要沿模型外部人为地截断边界,要求该边界能够吸收所有出射波且消除声波在边界的反射。目前,诸多学者提出多种吸收边界条件,但是受边界吸收角度的限制,未能达到理想的吸收效果[35]。完美匹配层(perfect matched layer,PML)是Berenger[36]针对电磁波传播情况提出的一种吸收边界条件,应用PML研究声固耦合系统的声辐射问题时,PML区域内声学波动方程中声压的坐标向量由实坐标转换为复数坐标,在该坐标中引入吸收函数使声波在进入PML层后逐渐衰减,最终实现出射声波的完美吸收。PML域内的声波方程表示为[37]

(13)

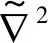
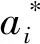
(15)

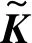
(16)

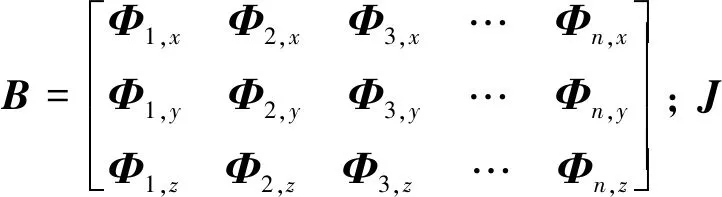
忽略外载荷及阻尼影响,式(15)演变为PML域内的声学特征值方程,表示为

(17)

PML不受边界吸收角度的限制,可以完全吸收任意方向和频率的波而不产生边界反射,因此选取完美匹配层吸收边界构建外声场有限元模型。基于软件COMSOL在结构-内声场耦合有限元模型外构建球形完美匹配层。建模时球体半径设置为目标模型半径的2至4倍。PML层网格大小至少为最小波长λmin的八分之一,结构-内、外声场耦合有限元模型如图3所示,其中内声场包含216 958个四面体网格,外声场包含10 520 860个四面体网格,PML层由677 552个棱柱网格构成。

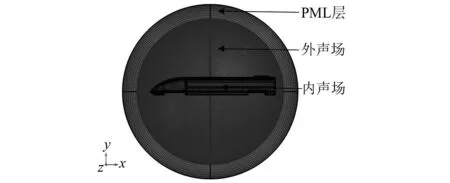
图3 结构-声场耦合有限元模型Fig.3 Structure-acoustic coupling finite element model

表4为结构-内、外声场耦合系统模态,图4为相应的模态振型云图。对比表4与表2,发现由于内、外声场的作用,车身结构模态固有频率整体下降,且前6阶均为新增加的模态振型。对比表4与表3,发现耦合声场第4阶与非耦合声场第1阶模态振型相同,固有频率略有降低;由于内、外声场的耦合作用使车内声压发生变化,产生新的内声场模态振型,内部声压除了沿纵向变化外,还沿着横向和垂向变化;随着阶数增加,声场振型逐渐向高阶演变。表4与表2、表3综合对比,发现前6阶耦合模态频率值与非耦合结构模态频率值相近,而与非耦合声场模态频率值差距明显,表明耦合系统模态主要受车身结构影响,内、外声场对耦合模态的贡献较小。

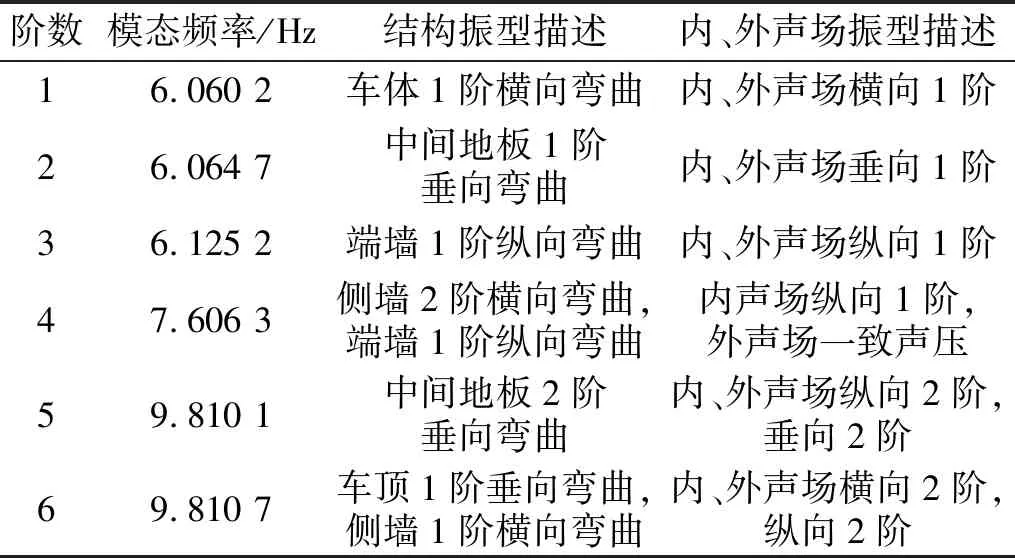
表4 结构-声场耦合模态Tab.4 Structure-acoustic coupling modes

图4 结构-声场耦合模态振型Fig.4 Structure-acoustic coupling mode shapes

对比该耦合系统中的内声场模态与外声场模态振型,发现两者振型基本一致(除了第4阶外声场模态振型为一致声压)。振型耦合系数反映了结构与声场子系统的模态振型耦合强弱,该系数与耦合面上结构和声场的模态振型有关。该系数绝对值越大,子系统间的耦合越强,反之则表示子系统间的耦合较弱。对于具有复杂几何构型的工程装备(如本文的头车声固耦合系统),模态振型耦合系数可以通过有限元方法获取。

忽略式(6)中结构与声场形函数矩阵及声腔密度参数,形成积分形式的振型耦合系数Oij

(18)

利用有限元法获取耦合面上外声场和结构子系统模态振型在各个节点上的分量,将声腔和结构的模态振型函数转换为节点编号为自变量的函数,代入式(18)后可写为[38]

(19)

式中:q为耦合面上的节点编号;qall为耦合面上的总节点数。

表5显示了该头车声固耦合系统的振型耦合系数有限元结果。从表中可以看出,在该耦合系统中,振型耦合系数的绝对值较小,均小于0.1。这表明该耦合系统的结构和声腔子系统较为复杂,导致其模态振型分布不规则,使得耦合面上的结构和声腔振型的相似度降低,因而振型耦合系数普遍较低。另一方面,这也反映了该耦合系统的结构与声场振型之间的耦合强度较弱。

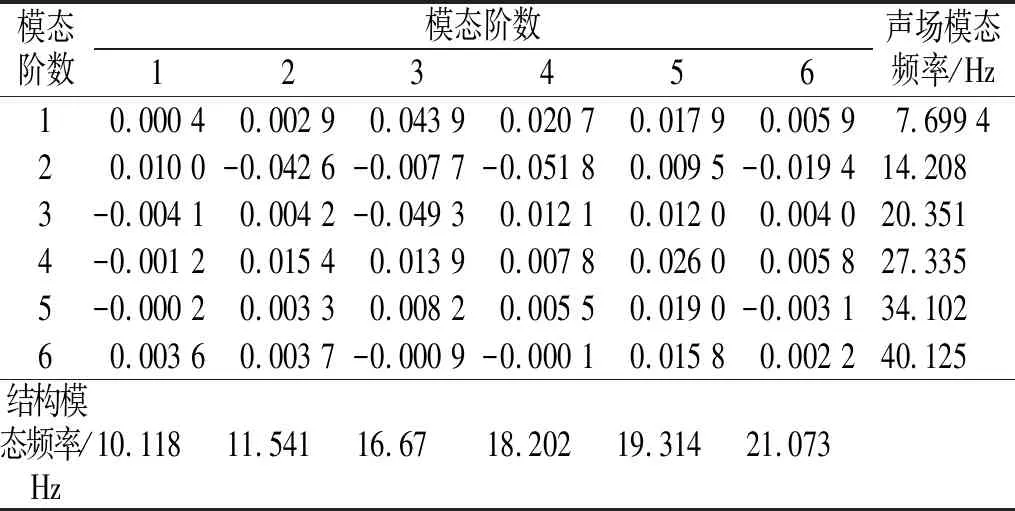
表5 振型耦合系数有限元计算结果Tab.5 FEM result of the mode shape coupling coefficient

4 头车减重优化设计

4.1 优化问题

本优化设计旨在保证车体结构本征动力学特性不降低的情况下,实现动车组头车结构质量最小化。

(1)设计变量

将车体结构板厚作为设计变量。由于将实体型材结构等效为NVH三层板结构,分配设计变量时先将头车结构划分为3个主要部分,即地板、侧墙、车顶(端墙部位对于车体质量变化影响程度较小,不作为设计变量),每部分进一步分为外蒙皮、中间层、内蒙皮等3个变量。由此确定9个部分的板厚作为优化设计的变量,即X=[x11,x12,x13,…,x31,x32,x33]T。

(2)约束条件

①频率约束:结构一阶垂向弯曲振动频率f不低于初始值。

②边界约束:又称为区间约束,规定了设计变量的取值范围。对于高速动车组车体结构,其板厚可以根据经验和工艺条件等因素确定变化的上下限,具体值见4.3节中表6。

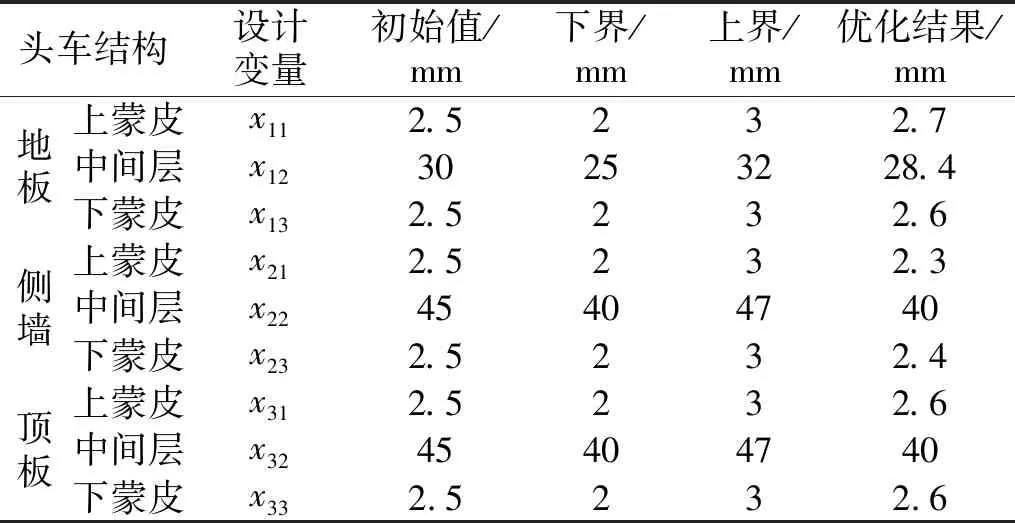
表6 减重优化结果Tab.6 Weight reduction optimization results

(3)优化模型

根据以上对高速动车组车体减重优化的参数选取及描述,该优化设计的数学模型表示为

(20)

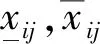
4.2 优化算法

本次优化设计基于有限元分析软件COMSOL优化平台,该平台提供了梯度算法和无梯度算法两类优化算法。梯度算法适用于目标函数可微或连续的情况,优化速度较快,但容易陷入局部最优。无梯度算法不依赖目标函数导数信息,只需要对目标函数进行采样,根据采样结果确定下一步的搜索方向。该算法适用于目标函数不可微或不连续的情况,优化稳定性较好,计算时间较长。考虑到优化的稳定性,本文选取无梯度优化算法中的Nelder-Mead算法。该算法通过在控制变量空间中构造由N+1个点组成的单纯形,其中N为控制变量的数量,对单纯形中的最差点进行反射、展开和收缩以改进单纯形的形状和位置,从而逼近目标函数的最优值。

Nelder-Mead算法使用优化容差(默认值为0.01)作为终止条件,该参数可用于判断优化是否收敛,反映了优化进程中目标函数值的变化幅度。迭代过程中,在优化步长大于或等于优化容差的比例控制变量中,无法找到改善当前目标函数值的方向时,该算法就会停止迭代,输出最优解。

4.3 优化结果

根据Nelder-Mead算法经过约1 000次迭代计算,获得了可行域内的优化解,优化过程中目标函数的迭代历史如图5所示,由于该算法每次迭代仅沿着单纯形的边移动到相邻顶点,而非直接向最优解方向前进,因此存在多余的转弯和折返,在该图中表现为前100次迭代优化幅度及振荡性较大,后期缓慢下降。优化后的设计变量值如表6所示。

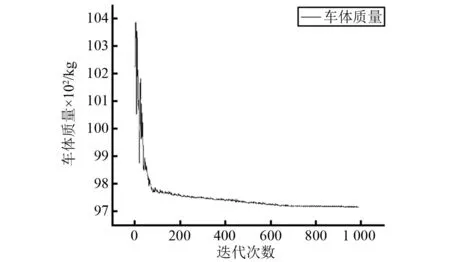
图5 减重优化迭代历史Fig.5 Iterations of weight reduction optimization

从表6可以看出,由于目标函数设置为车体质量最小化,大多数部位的板厚有所下降,优化后侧墙和顶板的中间层厚度甚至达到下限,而地板上下蒙皮及中间层、顶板上下蒙皮的对应厚度在优化后略有增加。这是因为在减重进程中受到一阶垂弯模态频率约束的限制,为保证车体本征动态特性不劣于初始值,需要适当提升部分位置的厚度,导致部分设计变量未能达到限值。优化后车体结构质量由10 225 kg降低到9 715 kg,相对减重率为5%,同时结构一阶垂弯模态频率也控制在初始值以上,为19.314 Hz,满足设计要求。因此,优化结果有效且可行。

5 耦合共振多目标优化设计

5.1 优化问题

本节在车体减重设计模型的基础上,进一步考虑结构与声场的耦合共振问题。对比非耦合结构和声场模态分析结果,发现结构第12阶模态频率(27.087 Hz)与声场第4阶模态频率(27.335 Hz)最接近,产生耦合共振作用的概率较高,易导致声腔内部声压升高、结构振动剧烈,降低旅客乘坐舒适度。因此,为消除耦合共振影响,将该结构与声场模态接近的固有频率差最大化作为另一个优化目标,形成头车轻量化与舒适性指标同步提升的多目标优化体系。优化设计的变量与减重优化相同,不再重复说明。

(1)约束条件

①频率约束:结构一阶垂向弯曲振动自振频率f不低于初始值。

②边界约束:设计变量取值范围与上节一致。

(2)优化数学模型

根据以上对高速动车组车体多目标优化的参数选取和描述,其优化数学模型可以表示为

(21)

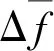
5.2 优化结果

经过209次迭代,获得了可行域内的优化解,优化过程的目标函数迭代历史如图6所示,优化前期目标函数波动较大,曲线振荡,后期逐渐趋于稳定。优化后的设计变量值如表7所示。

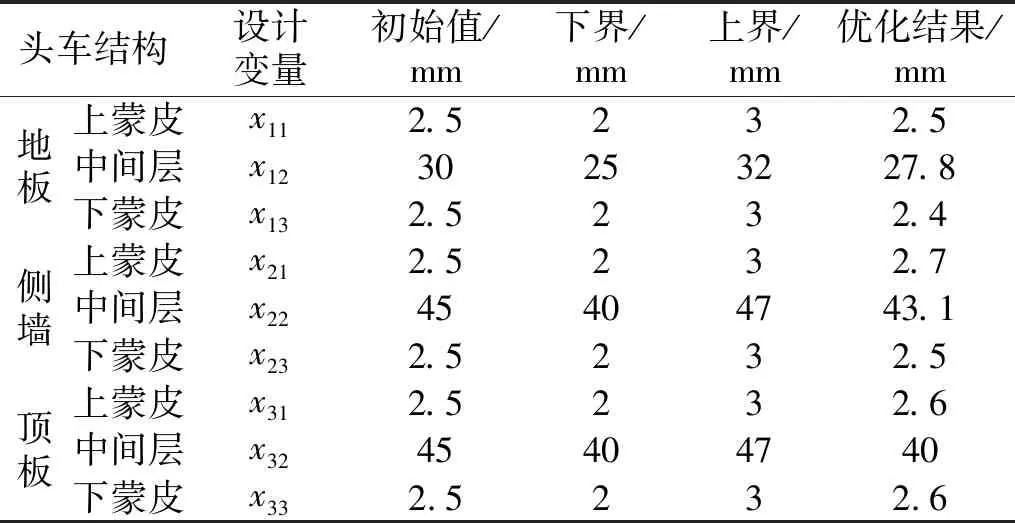
表7 多目标优化结果Tab.7 Multi-objective optimization results

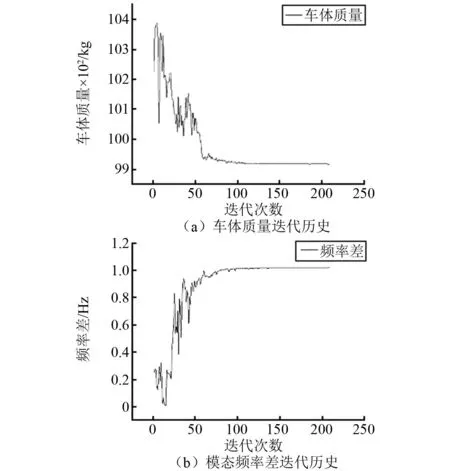
图6 多目标优化迭代历史Fig.6 Iterations of multi-objective optimization

由表7可以看出,地板中间层、侧墙上蒙皮及中间层、顶板上下蒙皮的厚度优化后略有增加,地板上蒙皮、侧墙下蒙皮厚度保持不变,顶板中间层厚度优化后达到下限。相较于减重优化,本模型引入频率差作为另一个优化目标,导致优化后达到下限的设计变量进一步减少。车体结构质量由10 225 kg降到9 916.4 kg,相对减重率为3%。此外,结构模态频率由27.087 Hz下降至26.315 Hz,声场模态频率保持不变,为27.335 Hz,两者模态频率差由0.25 Hz提高到1.02 Hz。结构一阶垂弯模态频率控制在约束值以内,为19.314 Hz。

6 结 论

本文基于模态等效和质量等效原则建立动车组头车有限元模型,分析了结构和声场模态的振型特征,进一步考虑内、外声场对结构的反馈作用进行结构-内、外声场耦合模态分析。基于模态分析结果,在保证车体结构的动力学特性前提下,构建了动车组头车结构的减重优化模型。最后在该减重优化模型的基础上进一步提取结构和声场固有频率值接近的非耦合模态阶次,将二者的频率差最大化也作为优化目标以避免耦合共振的影响,形成头车轻量化与舒适性指标同步提升的多目标优化体系。主要研究结论如下:

(1)车体一阶垂向弯曲频率符合轨道车辆设计规范。声场与结构模态存在相近频率值,增加车内声场与车身结构耦合共振概率,影响列车运行安全性和旅客乘车舒适性。内、外声场的耦合作用导致结构模态固有频率略有降低,产生新的固有频率和声场模态振型,论证了模态分析中考虑声固耦合因素的必要性。耦合系统模态主要受头车结构影响,声场对其贡献较小。

(2)减重优化效果为:车体结构质量降低510 kg,相对减重5%,且保持结构动力学特性优于初始状态。多目标优化后,车体结构质量减重3%,同时结构与声场模态频率差由0.25 Hz提高到1.02 Hz,有效避免声固耦合共振影响。