考虑结合面接触刚度的机床床身动态特性分析

刘书晟, 史 军, 孙建宏, 秦文强, 曾艳泓, 张 松

(1.山东大学 高效洁净机械制造教育部重点实验室,济南 250061;2.济南二机床集团有限公司,济南 250022; 3.重庆机床(集团)有限责任公司,重庆 401336)

机床的部件主要通过螺栓固定,这种连接方式便于拆卸,但引入了一个大的结合面,导致整个床身不连续,从而影响床身的动态特性[1]。整个机床结合面的接触刚度占机床总刚度的60%～80%[2]。为了设计、开发高精度机床,应当准确地获取机床动态特性参数。

从微观上揭示结合面接触机理是获得结合面接触参数行之有效的方法。Greenwood等[3]假设结合面上微凸体的高度遵循正态分布,提出了GW模型。之后基于GW模型建立的CEB[4]、KE[5]、JG[6]、Brake[7]模型都将微凸体之间的接触视为与球形微凸体的正接触。但是研究表明结合面上微凸体之间的接触大多是侧接触,而不是正接触。Gorbatikh等[8]提出了接触角分布函数来模拟微凸体的侧接触。事实上,在载荷作用下微凸体下的基体也会有相应变形。Iida等[9-10]研究了基体变形对结合面接触特性的影响。Ciavarella等[11-13]对微凸体间相互作用的接触机理进行了分析。

在考虑结合面接触刚度的机械设备动态特性研究方面,20世纪70年代Masataka等[14]进行了一系列试验研究,总结出了机床螺栓结合面的接触刚度和阻尼与接触面积之间的经验公式。黄玉美等[15]在此基础上考虑了结合状态、其他机械系统零件以及处理方法的影响,并提出了新的经验公式。王立华等[16]结合理论模态分析和试验模态分析,对某铣床的关键结合面动态特性参数进行了识别。然而,这些研究都是基于试验结果,存在工作量大、数据不完整等缺点,无法满足工程分析和设计的要求。为了弥补试验方法的不足,陈虹旭等[17]基于修正的分形理论,识别结合面处的接触特性参数并应用在有限元模型中,通过试验验证了理论模型的正确性。付振彪等[18]基于Hertz接触理论推导出结合面接触刚度的计算公式,并采用多单元混合的方法划分网格,建立整个进给系统的有限元模型,对滚珠丝杠进给系统进行了动态特性分析。Fan等[19]建立了一个考虑微凸体侧接触及相互作用的结合面法向刚度接触模型,并将其运用在有限元的结合面模型当中。以上方法接触刚度的计算方法不够准确,且有限元模型的约束方式还需要验证。

迄今为止,有关结合面刚度计算的研究不够完善只有少数接触刚度预测模型耦合肩-肩接触,基体变形和微凸体相互作用;少有研究验证了不同材料结合面有限元模型的准确性。本文通过弹簧单元来模拟结合面螺栓处的动态特性,建立了一种考虑结合面法向接触刚度的有限元模型。并通过试验值与仿真值的对比验证了有限元模型的准确性和普适性。

1 机床结合面接触特性分析

1.1 微凸体接触统计模型

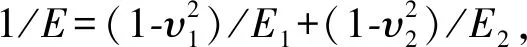
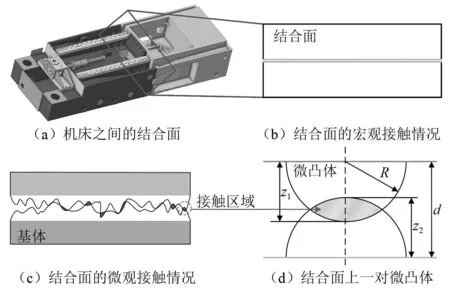
图1 结合面之间的接触Fig.1 Contact between joint surfaces

Kogut等在考虑弹性、弹塑性、全塑性接触行为的情况下,利用有限元分析给出了单个微凸体的接触载荷和变形之间的经验表达式。并推导了假设微凸体高度分布的结合面接触刚度的表达式。整个结合面的法向力和法向接触刚度计算公式为

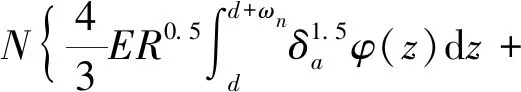
(1)

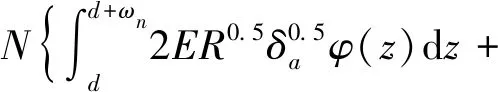
(2)

式中:N为微凸体的数量,N=nAn;n为微凸体分布密度;An为标称接触面积;φ(z) 为遵循高斯分布的高度的概率密度函数;R为微凸体半径;δa为微凸体变形量;δc为标定弹性变形和弹塑性变形之间转换的无量纲临界变形量。

Kogut-Etsion模型将所有微凸体接触看作峰-峰接触,实际上大多数微凸体接触是肩-肩接触,如图2所示。考虑接触角度对结合面之间实际接触的描述更加准确。

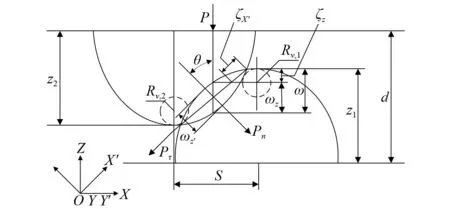
图2 一对肩-肩接触的微凸体Fig.2 A pair of asperities in shoulder-shoulder contact

在垂直于接触面的法向压力P的作用下,上下结合面发生变形。d为两个接触面之间的距离,s为上下表面中两个微凸体对称轴之间的距离。法向压力P可分为两个压力分量,即法向压力Pn和切向压力Pτ。θ为接触角,ωz和ωz′分别为Z和Z′方向上的接触变形。在Z方向上,侧峰接触对的总变形量为ω。用肩-肩接触变形ω代替峰-峰接触变形δa所得结果更为准确。根据几何关系,接触变形和接触角的表达式如下

(3)

(4)

KE模型不考虑基体变形,实际上微凸体的法向总位移ω等于微凸体变形ωa与基体变形ωb之和。为了考虑基体变形,建立了微凸体-基体系统模型,如图3所示。Li等使用不定点迭代法推导出了三个不同变形阶段的接触变形ω与微凸体变形ωa之间的关系式

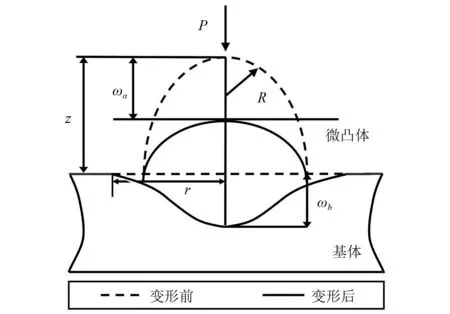
图3 微凸体-基体接触系统Fig.3 Asperity-substrate system

(5)

(6)

(7)

式中:κ1=Ea/Eb,κ2=KH/Eb,κ2=H/Eb为结合面的材质特性参数;ξ1=1.5R0.5/rb,ξ2=0.5πR/rb,ξ2=1.5πR/rb为微凸体的几何参数;R为接触微凸体的等效半径;rb为接触区域半径。

KE模型未考虑微凸体之间的相互作用,根据Bhattacharyya等[21]的研究,参考微凸体和同一平面第m个微凸体之间的平均距离可以表示为

(8)

式中:m为微凸体相互作用的阶次;Γ为伽马函数。用平均距离rm,代替微凸体之间距离r,相邻微凸体高度的变化可以表示为

由相邻微凸体的相互作用引起的参考微凸体高度z的变化可以表示为

(10)

微凸体相互作用是指微凸体之间的相互干涉导致基体变形。在宏观层面上看,这种相互作用表现为整个结合面平均高度的降低。由微凸体相互作用产生的平均平面的下降可以通过下式计算

(11)

基于微凸体的相互作用,将微凸体高度z校正为z′=z-Δε,微凸体高度分布函数可以表示为

(12)

微凸体相互作用对结合面的影响主要体现在微凸体的平均高度的变化上。

1.2 结合面接触刚度的识别

通过白光干涉仪(WYKO NT9300)进行表面形貌测试。由于铸铁和矿物复合材料左右床身结合面的加工精度要求一致。测试所得两种材料床身的表面形貌如图4所示。通过白光干涉仪的测量,可以获得扫描粗糙表面的形貌数据(高度和坐标)。

图4 表面形貌Fig.4 Surface morphology

Greenwood[22]提出,使用椭球体来模拟接触面比使用球体更符合实际接触面积的形状。同时,提出了一种利用XZ和YZ平面的顶点半径计算椭球体等效顶点半径的方法。如图5所示,选择了XZ平面和YZ平面中的五个相邻数据点,并使用二次函数来拟合两个平面中的凹凸形状。可以根据XZ平面和YZ平面中的顶点的半径来计算微凸体的峰顶曲率半径。

(13)

(14)

(15)

(16)

式中:Rv为椭球形微凸体的峰顶曲率半径;R为椭球形微凸体接触处的等效半径;s为上结合面和下结合面中两个微凸体对称轴之间的距离。

识别离散点的几何特征,以获得关于微凸体的位置分布和几何形状的信息,包括微凸体的位置、高度和曲率半径。对微凸体进行统计分析后,可以得到结合面微凸体的特征参数,如表1所示。微凸体高度和微凸体间距符合高斯分布,微凸体峰顶曲率半径遵循伽马分布。

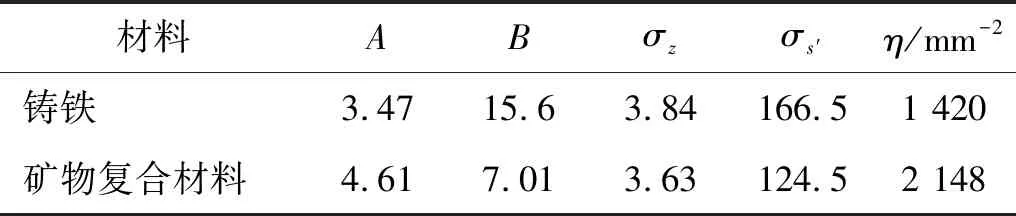
表1 表面形貌参数Tab.1 Surface parameters

微凸体的高度和间距遵循高斯分布,可以由下式得出

(17)

式中,σ为粗糙度高度和粗糙度间距的标准差。

峰顶的曲率半径服从伽马分布,伽马分布的概率密度函数可以通过下式表达

(18)

式中:A为形状参数;B为比例参数。

两种床身材料的材料属性如表2所示,图6显示了所建立模型预测的接触刚度随载荷变化的曲线。对比两种材料载荷刚度曲线,发现同载荷下铸铁材料的接触刚度大于矿物复合材料,并且随着接触压力的增加,两种材料之间的接触刚度差异变得更加明显。

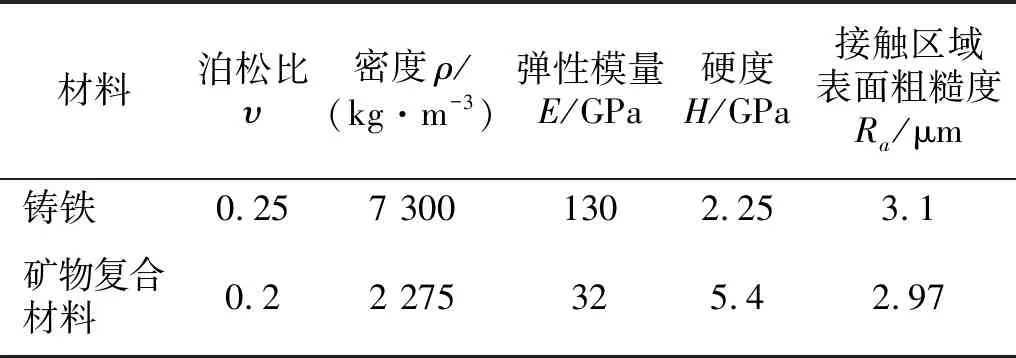
表2 材料属性Tab.2 Material properties

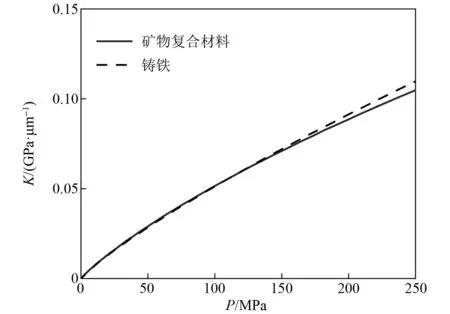
图6 两种材料法向接触刚度随法向载荷的变化规律Fig.6 The change of normal contact stiffness of two materials with normal load

2 动力学特性仿真过程

2.1 有限元模型

为了提高有限元模型的运算效率,将两种材料床身三维模型进行简化。铸铁材料床身简化后的结构如图7(a)所示。由于矿物复合材料的弹性模量和强度低于铸铁并且难以加工,因此在将铸铁床身转化为复合材料床时,应适当调整结构。矿物复合材料床身简化后结构如图7(b)所示。

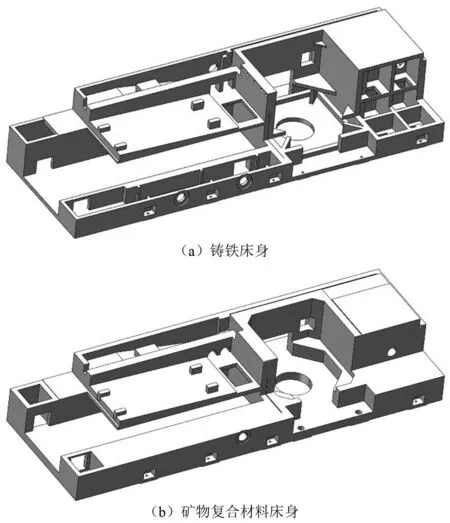
图7 机床床身三维结构模型Fig.7 Three dimensional structure model of machine tool bed

2.2 网格无关性分析和边界条件设置

针对两种材料的机床床身采用ANSYS有限元软件对其进行了网格划分,分别取网格尺寸为20 mm、18 mm、16 mm、14 mm、12 mm、10 mm、8 mm、6 mm,产生不同疏密度的网格模型,进行网格无关性验证,仿真结果如图8所示。

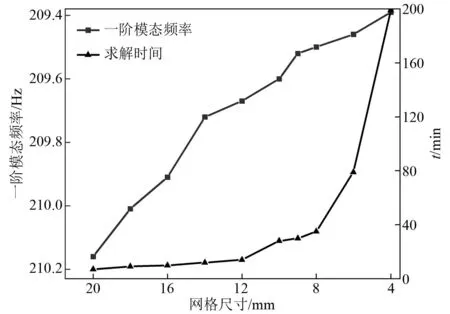
图8 一阶模态频率与求解时间随网格尺寸的变化Fig.8 The variation of no.1 modal frequency and solution time with grid size

随着网格尺寸的减小,计算时间随之增大,且越来越快。同时,一阶床身模态频率随之减小,当网格尺寸减小到8 mm时,减小幅度出现拐点,其后继续减小网格尺寸时,计算结果的减小幅度降低,然而求解时间大大增加,使得计算效率明显降低。因此,认为当网格尺寸为8 mm时,基本达到了网格无关性的要求。

通常情况下,机床左右床身结合面使用绑定接触,但是采用弹簧单元约束更加符合实际情况。由于机床受到载荷后,机床的结合面随即产生运动趋势,于是在结合面处产生了法向接触刚度。本文通过法向接触刚度预测模型对机床床身结合面的动态特性参数进行识别。

如图9所示,铸铁材料左右床身由5个M22螺栓和8个M20螺栓连接结合面A1,矿物复合材料左右床身由9个M22螺栓连接分别连接结合面B1和结合面B2,根据Zou等[23]的研究,10%左右的螺栓拧紧力矩T1形成预紧力F,即F=0.1T1(2π/pt)。其中pt为螺栓螺距,通过计算得到M20螺栓预紧力为146 000 N、M22螺栓预紧力为117 000 N。据此可得作用在结合面上的压强值,根据法向接触刚度-法向接触载荷曲线得到单位面积上的法向接触刚度。根据吉村允孝整理得出的平均接触压力与等效单位面积弹簧刚度值的关系可以得到机床结合面切向接触刚度。铸铁和矿物复合材料床身结合面切向刚度分别为6.8×1011N/m和4.2×1011N/m。切向弹簧布置在结合面的四个角。由于左右床身结合面面积较大,因此将法向弹簧单元布置在螺栓孔处,每个弹簧单元的动态特性参数只需将总刚度值均分到各个弹簧单元上即可,如表3所示。所研究的两种材料床身结构复杂,体积和质量较大,机床床身下有12个地脚螺栓,在建立有限元边界条件时设定地脚螺栓位置为绑定约束。

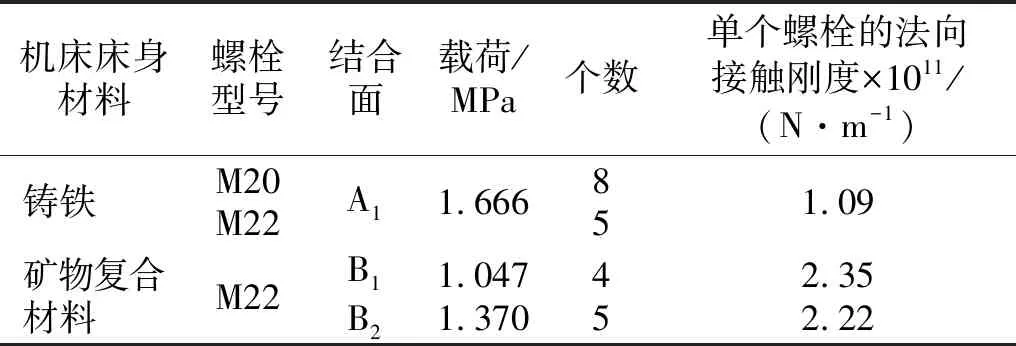
表3 结合面螺栓所受压强及法相接触刚度

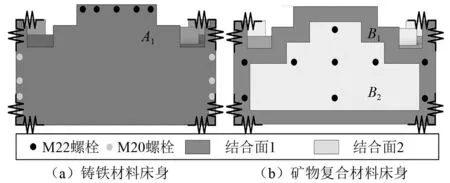
图9 机床床身结合面示意图Fig.9 Schematic diagram of the joint surface of themachine tool bed

2.3 有限元仿真结果

对有限元模型进行分析求解,计算得到两种材料床身的模态频率和振型。机床床身的前六阶模态频率如表4所示。不同材料和不同约束方式均未对振型造成影响,机床床身前6阶振型一致,如图10所示。

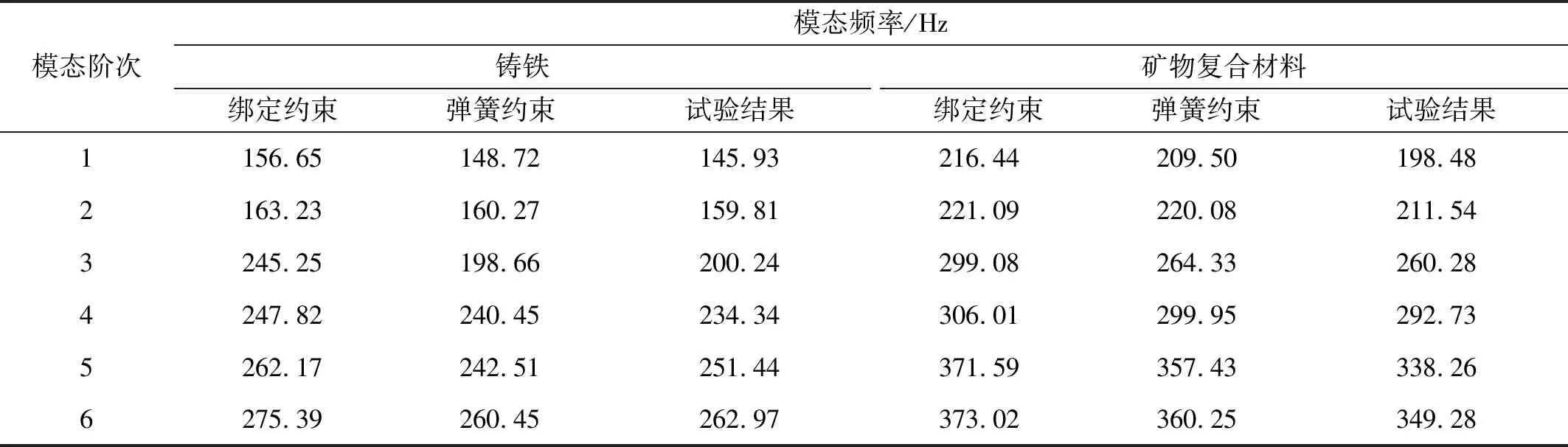
表4 不同约束条件下机床床身前六阶固有频率Tab.4 The first six modal frequencies of machine tool bed under different constraint conditions

图10 两种材料床身振型图Fig.10 Vibration diagram of machine tool bed of two materials

3 床身模态试验

3.1 试验设置

试验模态分析程序使用单输入多输出(single input multi outpu,SIMO)方法进行。在模态试验过程中,使用力锤(LC1304B-200KN)撞击激振点,产生力信号和振动信号,布置在指定测试点的加速度传感器(DH1A347E)收集振动信号。采集到的试验数据通过数据线从数据系统(DH5922D)采集传输到计算机,然后进行分析和计算,如图11所示。

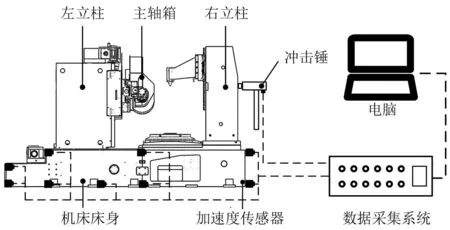
图11 模态试验测试系统Fig.11 Diagram of experimental modal test system

根据机床床身的三维模型及实际装配条件下的可测试区域,尽可能简化测量点的布置。测点设置如图12所示,模态试验共设置了28个测量点。

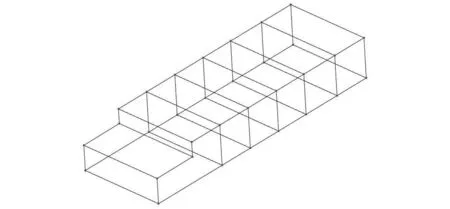
图12 模态试验测量点布置Fig.12 Layout of measurement points for modal test

3.2 试验结果及验证

通过对前六阶床身模态频率的分析计算,得到了如表5所示的模态频率。

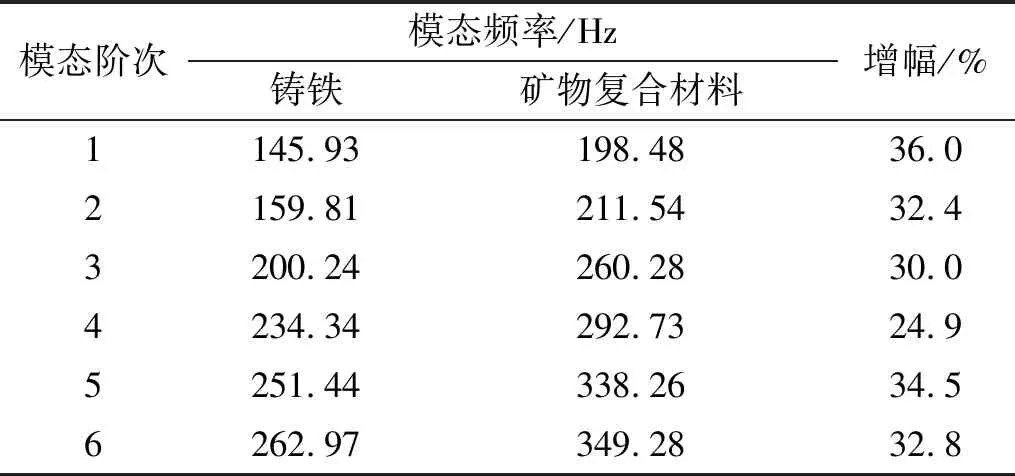
表5 两种材料机床床身模态频率对比

相干函数用于描述每个频率下两个信号之间的相关性。两个光滑随机过程X(t)和Y(t)的相干函数定义为

(19)

两种材料床身的前六阶模态频率在400 Hz内,在四个位置截取400 Hz内的相干函数图像,并标定出前六阶模态频率,观察模态频率处的相干性和判断数据的可靠性。从图13可以看出,两种材料床身六阶模态频率下的相干函数均大于0.8,由此可以判断本试验的数据可靠。

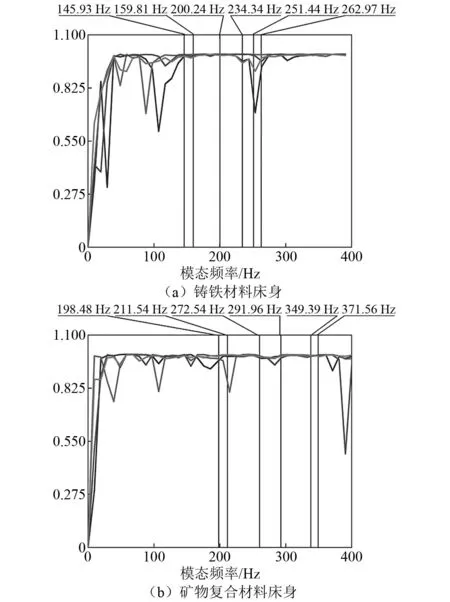
图13 两种材料床身的相干函数Fig.13 Coherence function for the machine tool bed of the two materials

为了评估模态试验结果的正确性,评估模态置信水平(model assurance criterion,MAC)是评估试验模态形状相关性的重要指标[24],可以表示为

(20)

式中,φi和φj是模态振型向量。

MAC取[0,1]范围内的实际值。接近1的系数表示完全模式匹配,而接近0的值表示相关性差。图14显示了该模态试验的MAC结果,可以得出两种材料床身试验所得结果可靠的结论。

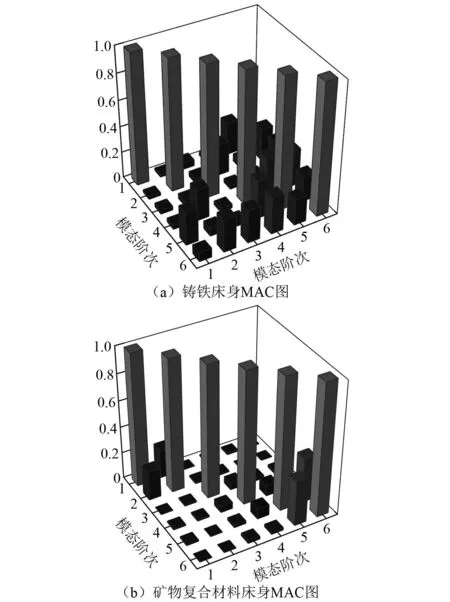
图14 两种材料床身MAC图Fig.14 Mac diagram of two materials of machine tool

4 结果与讨论

4.1 模型的有效性

通过有限元模态分析,可以得到在绑定条件和弹簧单元约束条件下的左右床身结合面的有限元分析模态结果。将有限元分析所得模态和试验所得模态数值进行对比。如图15所示,相比于绑定边界条件,基于本文法向刚度预测模型所建立的弹簧单元边界条件下的前六阶模态频率与试验值之间的误差更小,且最大误差在10%以内,证明了本文所建立的有限元具有足够的精度。

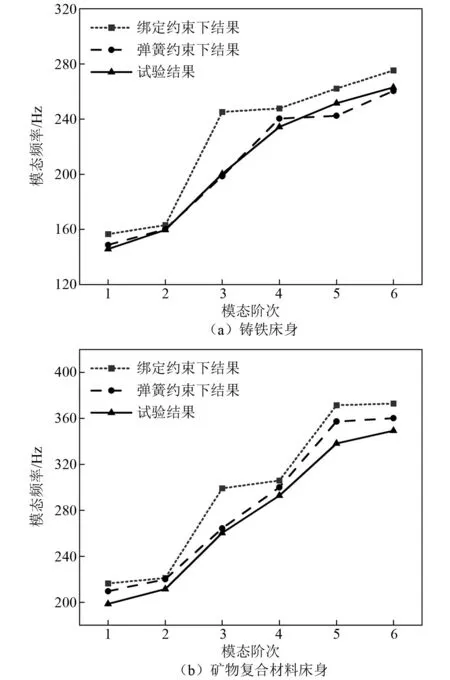
图15 不同约束方式下机床床身模态Fig.15 Modal analysis of machine tool bed under different constraint modes

4.2 模型的普适性

如图16所示,铸铁床身1阶、2阶、5阶、6阶模态误差均小于矿物复合材料床身的模态误差。基于弹簧单元约束的有限元模型识别铸铁床身的动态特性相比于矿物复合材料床身更为准确。对于矿物复合材料床身,有限元模型模态误差较小,均小于10%。说明本文有限元模型具有普适性。

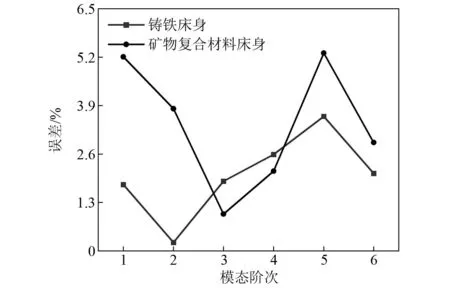
图16 机床床身模态频率与试验模态频率误差Fig.16 Error between modal frequency of machine tool bed and experimental modal frequency

4.3 材料的影响

两种材料机床床身动态特性变化如图17所示,矿物复合材料床身的前六阶模态频率均高于铸铁材料床身。且矿物复合材料床身的一阶模态频率提升最大,约为36%。在实际加工中可以有效避免共振现象的发生,有利于提高机床的加工精度和加工质量。结果表明矿物复合材料床身结构的抗振性能要比铸铁好,具有良好的动态性能。

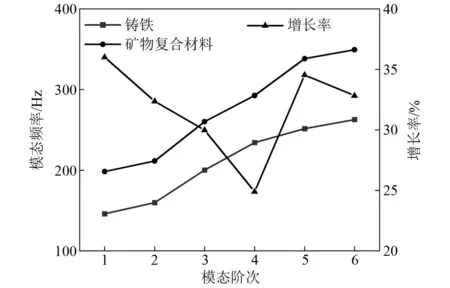
图17 不同材料机床床身模态Fig.17 Modal analysis of machine tool bed made by different material

5 结 论

以铸铁和矿物复合材料机床床身结合面为研究对象。通过建立的接触刚度预测模型得到了结合面上螺栓的接触刚度。建立了基于弹簧单元约束的有限元模型。另一方面进行了两种材料床身的模态试验。根据试验与有限元结果的对比,可以得出以下结论:

(1)建立了接触刚度预测模型,对不同材料床身结合面接触刚度进行计算,结果表明相同载荷下铸铁材料床身的接触刚度大于矿物复合材料床身,并且随着接触压力的增加,两种材料之间的接触刚度差异变得更加明显。

(2)基于本文法向刚度预测模型所建立的弹簧单元约束条件下的前六阶模态频率与试验模态之间误差相比于绑定约束更小。且弹簧约束条件下最大误差在6%以下,证明了有限元模型的准确性。

(3)基于弹簧单元约束的有限元模型识别出的前六阶模态频率与试验模态频率之间的误差较小。且对于铸铁和矿物复合材料床身均适用,证明了模型的普适性。

(4)本文建立的考虑结合面接触刚度的有限元模型对铸铁床身和矿物复合材料床身进行了动态特性分析,计算出的矿物复合材料床身的前六阶模态频率均大于铸铁床身,并且两种材料床身的振型基本一致。