某埋头弹机枪弹膛驱动螺旋槽优化设计

刘强，周克栋，李东昊，陆野，任海钺，赫雷

（1.南京理工大学 机械工程学院，江苏， 南京 210094；2.国营第二九六厂，重庆 400050）

某埋头弹机枪为了可以发射塑料弹壳埋头弹，采用了弹膛、枪管分离的结构，在枪械自动循环过程中，由枪机框带动弹膛摆动，使得枪械在击发时，弹膛与枪管同轴对正；在枪械供弹/抛壳时，弹膛与枪管相互错开.枪机框带动弹膛摆动，是通过枪机框上的导柱与弹膛上的螺旋槽相互作用完成的.

枪械完成击发后，枪机框在导气室压力作用下开始后坐，经过试验研究发现，在枪机框导柱进入弹膛螺旋槽时，对螺旋槽冲击过大，这不仅使枪机框动能损失严重，而且会对枪机框上的导柱带来损伤，减少导柱寿命，本文将对螺旋槽的几何形状及动力学特性进行分析，从枪机框、弹膛的运动方程入手，通过优化弹膛螺旋槽的形状，降低导柱进入螺旋槽时对螺旋槽的冲击力.

而对于弹膛螺旋槽理论轮廓线的选型，本文采用5 次函数曲线来进行拟合，5 次函数曲线具有优良的平滑性[1]，被广泛地应用于凸轮设计[1]等方面，用于本文中弹膛曲线槽的设计，理论上既可以降低枪机框与弹膛曲线槽之间的刚性冲击，又可以降低两者之间的柔性冲击[2].李世康等[3]选用5 次函数曲线优化了高射速转管炮的凸轮曲线，刘海民等[2]选用5 次函数曲线作为凸轮槽的过渡曲线，但他们只是利用了5 次函数曲线可以平滑过渡的性质，并未从力学特性入手，优化5 次函数曲线.

1 目标函数的确定及优化原理

1.1 目标函数

本文所研究的枪机框、弹膛相互作用如图1 所示.图1 中导柱连接在枪机框上.由图1（a）～1（b）可见，当枪机框后坐时，枪机框上连接的导柱从枪口方向向枪尾方向运动，弹膛通过导柱与弹膛螺旋槽的相互作用，从发射位置摆动到供弹位置.弹膛摆动过程如图1（c）所示.

图1 弹膛摆动原理Fig.1 Chamber swing principle

将本文所述埋头弹机枪进行加工，并做射击试验，运用高速摄影拍摄枪机框运动，提取出枪机框的速度、位移曲线.

枪机框速度-时间曲线如图2 所示，将该曲线与试验测得的枪机框位移-时间曲线及本枪的自动循环图进行对比，可以清楚地知道速度曲线上任意一点对应的机构动作.图2 中，点1 为枪机框后坐时达到的最大速度，为7.72 m/s，从点1～2 的过程中，发生了枪机框导柱撞击弹膛螺旋槽壁起始部位的机构动作，因为枪机框导柱与弹膛螺旋槽之间发生撞击，使枪机框速度受到很大的损失；点2 的速度为3.21 m/s，而这次撞击，使得弹膛瞬间拥有了很高的摆动角速度；接着，弹膛通过螺旋槽又反向为枪机框加速，使枪机框的速度加速到点3 位置，为5.38 m/s，虽然弹膛的反向加速使得枪机框速度有所回升，但总体而言，枪机框与弹膛的撞击使得其速度从7.72 m/s 降低到5.38 m/s，损失达到30.3%，依然会使得后续机构动作能量紧张，而且，撞击过程中巨大的撞击力也极容易使枪机框上的导柱结构遭到损坏.

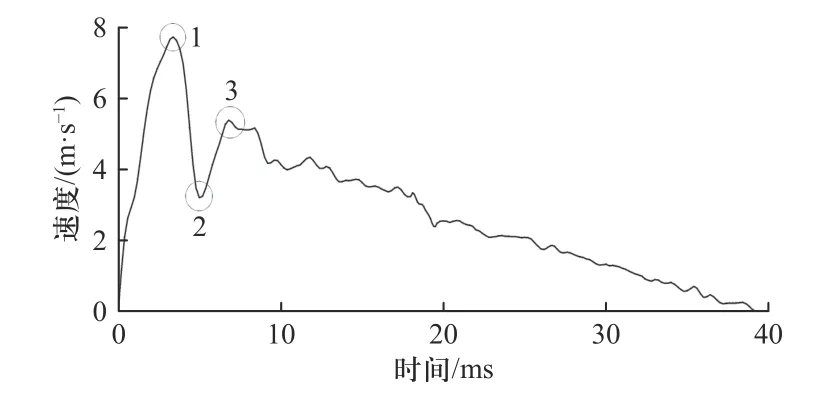
图2 枪机框后坐速度-时间曲线Fig.2 Bolt carrier recoil speed-time curve

在试验中，弹膛被机匣、节套等零部件包围，无法用高速摄影测量其摆动的速度曲线， 但弹膛摆动的角速度、导柱对弹膛的冲击力均可由仿真得到.

图3 为仿真得到的导柱进入弹膛螺旋槽时，对弹膛螺旋槽壁的冲击力及弹膛摆动的角速度-时间曲线.可以看出，在导柱进入弹膛时，会瞬间产生很高的冲击载荷，约为16.66 kN，而弹膛也会在受到载荷作用的同时，产生极高的角加速度，瞬间加速到点1处，点1 处角速度为23 771 (°)/s.参看图1（a）、1（b），导柱在进入弹膛螺旋槽之前，先在螺旋槽前端相连的直槽内运动，导柱在直槽内运动时，导柱与摆动弹膛之间的传速比为0，导柱的运动不会引起弹膛的摆动，但导柱进入螺旋槽的瞬间，导柱与摆动弹膛之间的传速比突然发生变化，造成导柱对弹膛的冲击及弹膛的瞬间加速.因此，优化弹膛的目的是降低枪机框导柱进入弹膛螺旋槽时对弹膛螺旋槽壁的冲击，其本质是通过改变螺旋槽理论轮廓线的形状，进而改变弹膛与枪机框导柱之间的传速比.

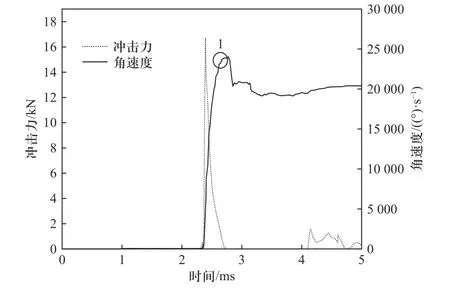
图3 导柱对螺旋槽壁冲击力及弹膛摆动角速度-时间曲线Fig.3 Curve of impact force of guide pillar on spiral groove wall and chamber swing angular velocity vs.time

本文将以枪机框导柱与弹膛螺旋槽传动的整个过程中，导柱对螺旋槽的最大冲击力最小为目标函数，求解一次传动过程中最大冲击力最小时对应的弹膛螺旋槽理论轮廓线.

1.2 优化原理

如图1 所示，因为枪机框始终做直线运动，即导柱轴线始终沿一条直线运动，而弹膛做回转运动，因此，导柱与弹膛螺旋槽的接触可简化为为点接触（暂不考虑零件弹塑性变形）[1]，且该点始终在一个水平面内，如图4 所示点P.

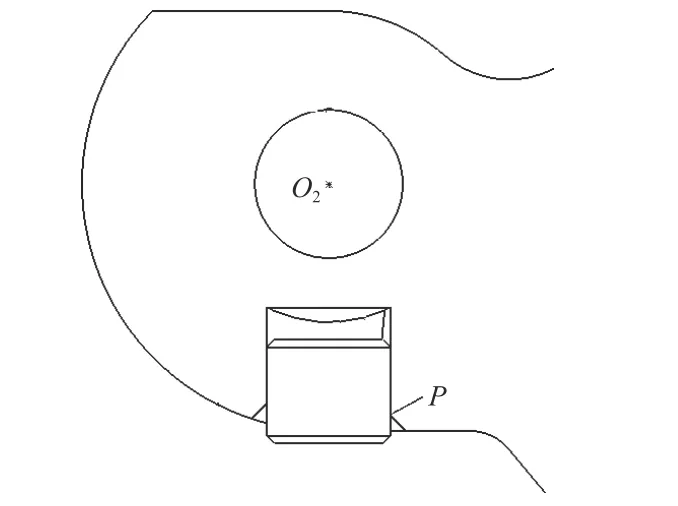
图4 螺旋槽、导柱接触点示意图Fig.4 Schematic diagram of contact points of spiral groove and guide pillar

将螺旋槽与导柱接触一边的轮廓线称作“实际轮廓线”，点P即始终在实际轮廓线上.假定弹膛不动，导柱沿弹膛螺旋槽运动，导柱横截面圆心滑过的轨迹称为“理论轮廓线”，现将理论轮廓线沿所在外圆柱面（该圆柱横截面圆心为图4 中O2）展开，即得到一条直线段AC.

如图5 所示，AC为螺旋槽理论轮廓线沿所在圆周面展开线，AB对应枪机框导柱掠过这段展开线时走过的位移，BC为弹膛摆动过程中，导柱横截面圆心在螺旋槽内滑过曲线在弹膛端面投影的长度，BC未展开前如图6 所示，弹膛摆动90°，BC即表示理论轮廓线在弹膛端面的投影为1/4 圆周长.

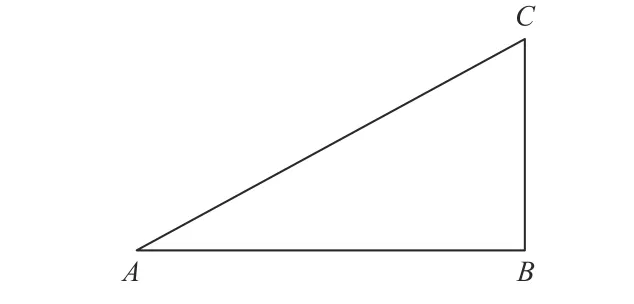
图5 螺旋槽理论轮廓线展开示意图Fig.5 Schematic diagram of expansion of theoretical contour line of spiral groove

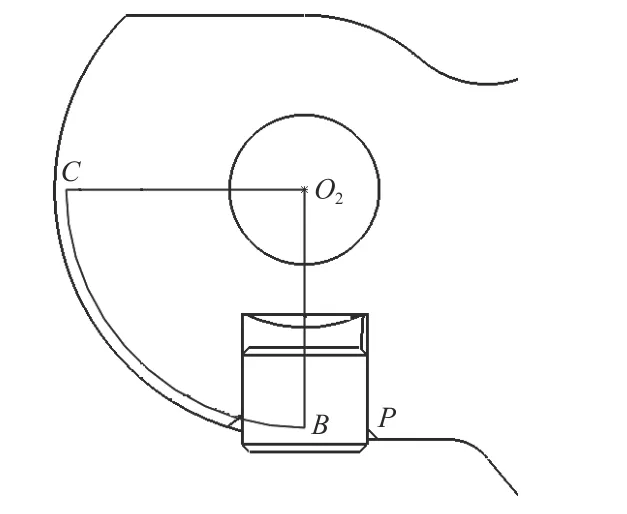
图6 BC 未展开前示意图Fig.6 Schematic diagram before BC expansion

在本文优化过程中，A、B、C3 点的位置不变，将线段AC用5 次函数曲线代替，使得1.1 节中所述的目标函数取最小值.5 次函数的表达式[1]为

式中：x为导柱螺旋运动中导柱随枪机框运动滑过的直线距离，x的最大值为AB的长度；y为导柱横截面圆心轨迹在弹膛端面的投影圆弧长度，y的最大值为弧BC的长度.继续假设弹膛不动，导柱沿着螺旋槽做螺旋运动，点A为螺旋槽理论轮廓线的起点，点C为导螺旋槽理论轮廓线的终点，将式(1)5 次函数的起点建立在点A，并以点A为原点建立平面直角坐标系，因为曲线过原点，且为了消除刚、柔性冲击，曲线在点A的1、2 阶导数均为0，则有a0=a1=a2=0，点A坐标为(0, 0)，点C坐标为(p,q)，(p,q)为已知值，由枪械具体结构决定.在AC段5 次函数曲线上再取2 个点[4-5]，这2 个点坐标为(p/3,y1)、(2p/3,y2)，假如这2 个点的坐标均已知，且点C坐标(p,q)也已知，则可以由该3 个点坐标求出式(1)中a3～a5的具体数值，即求出式(1)的具体形式，因此，y1、y2为待优化的变量值.

2 螺旋槽实际轮廓线方程

2.1 螺旋槽实际轮廓线方程

为了较为精确地研究螺旋槽实际轮廓线，现推导螺旋槽实际轮廓线方程，首先建立坐标系.

如图7 所示，在导柱上建立随动坐标系Osxsyszs，Os在导柱的轴线上，ys轴与导柱轴线重合，zs轴为枪机框后坐方向的反方向，即zs平行于枪管轴线，指向射击方向，Osxszs平面为水平面，导柱与螺旋槽的接触点P在该平面上.

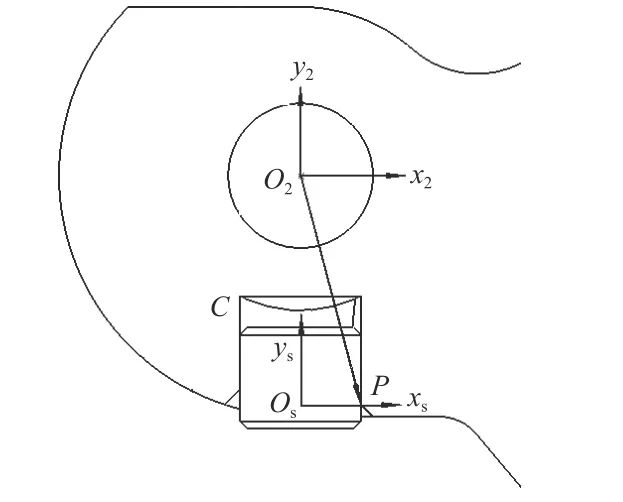
图7 弹膛螺旋槽坐标系统Fig.7 Coordinate system of spiral groove in chamber

如图8 所示，点P在随动坐标系Osxsyszs中的矢径为R1，R1与xs夹角为φ.

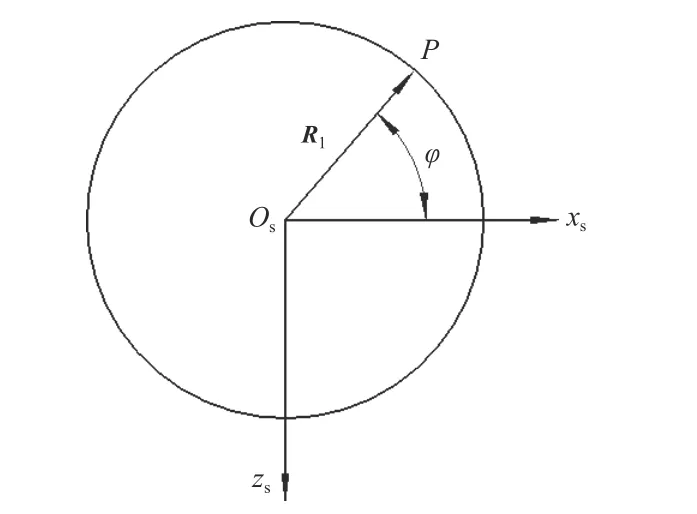
图8 点P 在随动坐标系Os xs ys zs 中的位置Fig.8 Position of point P in follow-up coordinate system Os xs ys zs

如图7 所示，在导柱起始位置建立定坐标系O1x1y1z1，起始时刻，O1x1y1z1与Osxsyszs重合.在弹膛回转中心轴端面建立定坐标系O2x2y2z2，O2与O1在同一竖直平面内，z2轴与弹膛回转轴重合，与z1轴平行，O2y2z2平面与O1y1z1平面共面.在O2x2y2z2坐标系中，点P的矢径为R3.

如图7 所示，在点O2建立固定在弹膛上的随动坐标系Ocxcyczc，点Oc与O2重合，zc轴与z2轴重合，在t=0 时刻，Ocxcyczc坐标系与O2x2y2z2坐标系重合.在Ocxcyczc坐标系中，点P的矢径为Rc.参考文献[1, 6]，可以根据坐标变换的方法，用点P在随动坐标系Osxsyszs中的矢径R1求出点P在随动坐标系Ocxcyczc中的矢径Rc，Rc的表达式即弹膛螺旋槽实际轮廓（工作曲面）的参数方程，求得Rc的表达式为

式(2)中：弹膛转过的角度τ为时间的函数，即τ=τ(t)；枪机框后坐位移s也是时间的函数，即s=s(t).

2.2 螺旋槽实际轮廓线接触方程

式(2)适合于螺旋槽工作面上所有点，要进一步确定螺旋槽工作曲线，即螺旋槽与导柱的接触曲线，就必须确定式(2)中φ与ε之间的关系，即螺旋槽工作面与导柱曲面的接触关系—接触方程[1].

虽然导柱与弹膛螺旋槽之间为点接触，但接触线光滑连续，根据微分几何包络理论[1,7]，它们之间的接触方程为：

式中Rcφ、Rcε、Rct分别为式(2)关于φ、ε、t的偏导，由式(3)可得：

式中：ω为弹膛摆动时的角速度；v为枪机框后坐速度；ω、v均是时间t的函数；k为枪机框对弹膛传动的传速比，k只与螺旋槽理论轮廓线的形状有关[8-9]；ε由枪械结构决定，螺旋槽优化并不改变已有的枪械结构，因此ε为定值；由式(4)可知，φ只与弹膛螺旋槽理论轮廓线的形状有关.

得到完整弹膛螺旋槽实际轮廓线方程[1]为

2.3 压力角分析

枪机框导柱与弹膛螺旋槽的接触简化为点接触，设接触点为图8 所示P点.在P点，导柱与弹膛螺旋槽之间接触力的方向过导柱水平截面的圆心，接触力在O1x1z1平面内，压力角α如图9 所示.

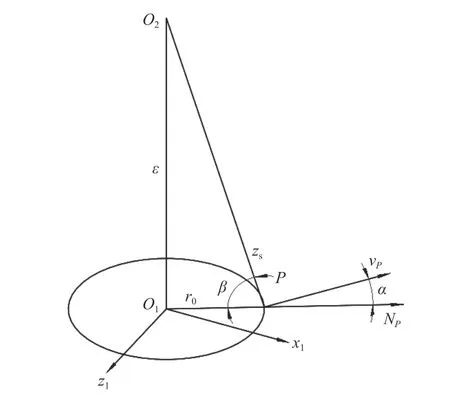
图9 导柱-弹膛传动压力角示意图Fig.9 Schematic diagram of pressure angle between guide pillar and chamber

在导柱与弹膛螺旋槽的传动中，导柱为主动件，弹膛为从动件，弹膛在P点的速度为vP，导柱对弹膛螺旋槽的作用力为NP，两者间夹角为α，可以看出，角β只与结构尺寸有关，即：

因此在导柱对弹膛的传动中，压力角为恒定值，减小r0或是增大ε都有助于压力角减小.在本枪械中，r0与ε均已确定，不宜再做改动，本文所述摆膛机构压力角只有14°，远小于同类圆柱凸轮的最大允许压力角60°[1]，满足传动要求.

3 枪机框、弹膛传动的力学分析

3.1 必要假设

本文对摆膛机构的优化将基于机构的动力学特性，为了建立相对准确的动力学模型，需要做出如下假设：

① 枪机框导柱实际结构为轴套结构，与弹膛螺旋槽之间的摩擦形式为滚动摩擦，因此两者之间的摩擦力及摩擦力做功忽略不计;

② 枪机框导柱在推动弹膛回转的过程中，导柱与弹膛间的撞击普遍存在，本文取两者间的撞击次数为实际轮廓线的离散点数，事实上，本文将弹膛螺旋槽实际轮廓线离散为241 个点[4]，并对每个点上枪机框导柱是否对拨弹杠杆造成冲击进行了判别，因此，这种处理方式较为准确地模拟了枪机框导柱与弹膛之间相互撞击的情况；

③ 撞击是瞬间完成的；

④ 撞击模型为纯弹性模型，不考虑撞击中的能量损失，而构件因为撞击而产生的动能变化由运动方程式(8)决定，撞击后，对撞物体可以瞬间恢复形变.

3.2 传动运动分析

在枪机框导柱带动弹膛做回转运动的过程中，各零部件的动能满足能量守恒，因此，可以列出枪机框与弹膛的运动方程[10]为

式中：mA为枪机框的质量；JB为弹膛的转动惯量（含弹壳）；vA为枪机框位移为z时的速度；vA0为枪机框导柱进入弹膛螺旋槽的初始速度；pA为作用到主动件上的火药燃气的压力；FA和FB分别为作用到主动件和从动件上的阻力；Rl为导柱与弹膛螺旋槽接触点到弹膛回转轴的距离，即图9 中|O2P|；ηp为传动效率；k为枪机框到弹膛的传速比，k=；k0为摆膛阶段开始时的机框、弹膛传速比，k0=0.

在枪机框导柱带动弹膛摆动时，导气室压力已为大气压力，不再对枪机框做功，因此pA=0；FA为复进簧阻力，可由复进簧参数写出具体表达式；在弹膛摆动过程中，受到的阻力主要为弹膛与弹膛回转轴之间的摩擦阻力，该阻力相对于复进簧簧力很小，可以忽略不计，即FB忽略不计.

3.3 传动接触力分析

本文中采用Hertz 接触理论计算导柱与弹膛螺旋槽相互碰撞时产生的碰撞力，该模型认为接触力是压入深度的非线性函数，且碰撞后参与部件可以弹性恢复，不存在能量损失，接触力表达式为[11]：

式中：δ为2 个接触刚体之间的相对压入量；K为接触刚度系数；n为力指数，由接触刚体的材料和接触区域的几何特性决定，对于金属接触，n取1.5[11].刚度K的计算式为

式中：r0为导柱半径；Rs为螺旋槽与导柱的接触点曲率半径；σR、σr与弹膛、导柱的材料参数有关，其计算式为

式中vl、El分别为材料的泊松比和杨氏模量.式(10)中由于螺旋槽接触点的曲率半径Rs远大于导柱半径r0，为简化计算，可以视Rs为无穷大[12]；将Rs趋于无穷大，对式(10)求极限，得：

如前文3.1 节所述，本文将弹膛螺旋槽理论轮廓线离散为241 个点，枪机框导柱与弹膛相互撞击的过程就是传动过程，假设在枪机框运动到了理论轮廓线上的第i个点，撞击之前，枪机框的速度为vAi-1，弹膛摆动角速度为ωBi-1，撞击后，枪机框速度为vAi，弹膛摆速为ωBi，其中，vAi-1、ωBi-1为枪机框导柱与弹膛在第i-1 点完成撞击（传速）后的速度，vAi-1方向为z1轴负方向.弹膛上与枪机框导柱接触点的速度方向为该点所在回转圆弧的切线方向，该速度即图9 中vP，接触力即图9 中NP，在第i点发生撞击之前，可以求出此时枪机框导柱、弹膛接触点在NPi方向的相对速度Δvi.撞击前，枪机框速度vAi-1与弹膛接触点线速度vPi-1见图10.

图10 撞击点撞击速度示意图Fig.10 Schematic diagram of impact speed at impact point

由图10 可得：

式中Rl为弹膛回转轴到接触点P的距离，即图9 中|O2P|.式(14)中，vAi-1为负值，ωBi-1为正值，但vAi-1与vPi-1在NPi方向投影同向，故vAi-1前需要加一个负号.式(14)中，若Δvi>0，则为导柱碰撞弹膛，此时参看式（15），则可以由能量守恒即可求出导柱与弹膛螺旋槽间的最大穿透深度μ.

将式(15)求得的穿透深度μ带回式(9)，则可以求出最大撞击力Fnmax，Fnmax即为一次碰撞的碰撞力.

式(14)中，若Δvi<0，则为弹膛撞击枪机框，此时，两者发生撞击的位置不在所求边线上.又因为在本枪械中，虽然会出现弹膛撞击枪机框导柱为枪机框加速的情况，但整个传动过程中，枪机框为主动件，枪机框的质量远大于弹膛的质量，枪机框在撞击弹膛前一瞬间所拥有的动能远高于弹膛摆动过程中拥有的最大动能.因此，枪机框对弹膛的最大冲击载荷远高于弹膛主动撞击枪机框时的载荷，在Δvi<0 时，直接取Fnmax=0.

3.4 优化过程

本文采用遗传算法[13]对弹膛螺旋槽理论轮廓线进行优化，首先由遗传算法的赋值程序为y1、y2赋值，生成5 次函数曲线上点(p/3,y1)、(2p/3,y2)的具体坐标，由这2 个坐标及曲线终点坐标(p,q)求出5 次函数曲线.现求枪机框运动到任意位置时，弹膛摆过的角度τ.

如图11 所示，假设枪机框从进入螺旋槽开始，后坐的距离为a时，导柱截面圆心滑过螺旋线在弹膛端面的投影为b，b值由5 次函数及此刻的a值求出，此刻弹膛转过的角度τ如图12 所示.

图11 理论轮廓线展开线上点示意图Fig.11 Schematic diagram of points on developed curve of theoretical contour line

图12 弹膛回转角度示意图Fig.12 Schematic diagram of chamber rotation angle

由图12 可知，

将曲线离散为241 个点，假设枪机框到i-1 个点时转过角度为τi-1，枪机框位移为zi-1，则该传动的传速比为：

由前文可知，导柱进入弹膛螺旋槽时，传速比为0，因此，k1=0，τ1=0，Fnmax=0，将传速比ki-1代入式(8)，即可求出枪机框、弹膛在i-1 点完成撞击时的速度，即在i点发生撞击前的速度；将ki代入式(4)，即可求出i点对应的角φi；进而由式(14)、(15)、(9)求出弹膛与导柱在第i点撞击时产生的接触力（第2 个点的接触力由枪机框进入螺旋槽时的初始速度求出.将241 个点的接触力都求出来，然后返回其中的最大值给遗传算法主程序，由遗传算法主程序进行优化，求解出最小接触力，此时对应的5 次函数曲线即为优化结果.

4 优化结果

将弹膛理论轮廓线展开线优化后的结果与优化前的结果对比，得到以下曲线.

图13 为弹膛理论轮廓线展开线优化前后对比图（实际轮廓线可由式(6)求解），可以看出，使用5 次函数曲线后，螺旋槽的入口端与出口端均比直线平缓.按照图13 所示弹膛理论轮廓线展开线重新加工弹膛，并做射击试验，将得到的枪机框速度-时间曲线与弹膛未优化时（即图2）的枪机框速度-时间曲线进行对比，得到速度对比图像如图14 所示.

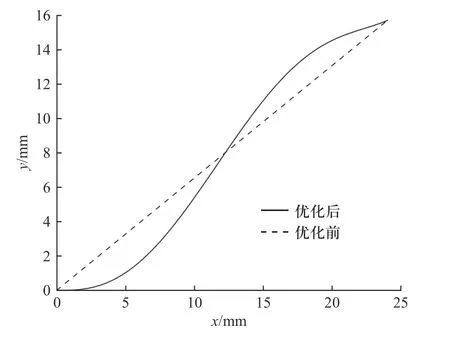
图13 优化前后弹膛理论廓线展开线对比图Fig.13 Comparison diagram of developed curve of chamber theoretical profile before and after optimization

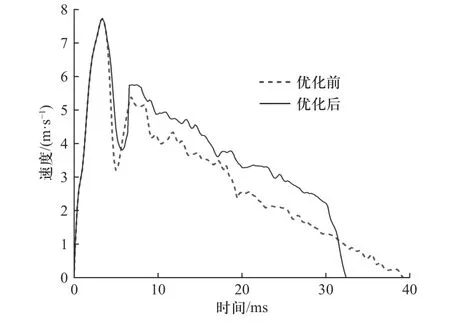
图14 弹膛螺旋槽优化前后枪机框速度对比图Fig.14 Comparison diagram of bolt carrier speed before and after chamber spiral groove optimization

由图14 可以看出，弹膛螺旋槽理论轮廓线优化后，枪机框导柱进入弹膛时，虽然依旧存在弹膛为枪机框反向加速的情况，但速度损耗明显降低，由原来的损失30.3%降低到损失25.6% (速度损失比例按1.1 节所述方法计算)，使得枪机框有了更加充足的动能完成后续的自动动作.现提取动力学仿真中枪机框导柱对弹膛的冲击力对比如图15 所示.

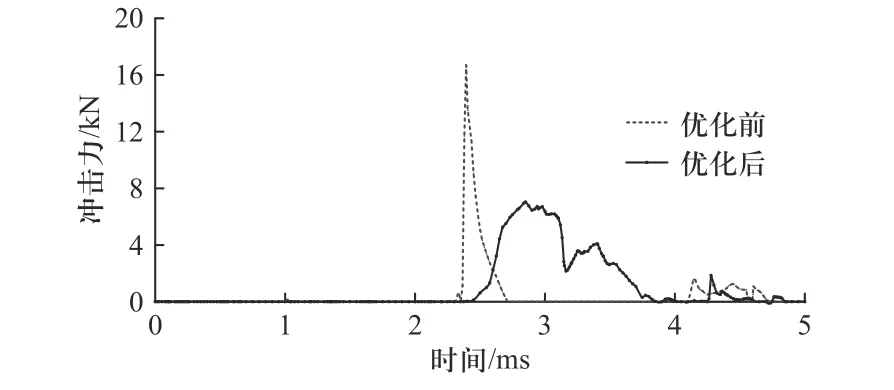
图15 优化前后导柱对弹膛螺旋槽壁冲击力对比图Fig.15 Comparison of impact force of guide pillar on spiral groove wall of chamber before and after optimization

图15 为导柱进入弹膛螺旋槽时的冲击力对比，由图可见：未优化前，导柱进入弹膛螺旋槽时的最大冲击力为16.66 kN，优化后为7.04 kN，优化后的冲击力为优化前的42.27%，降低了57.73%，优化效果显著，达到了预期目的.

5 结 论

本文针对某埋头弹机枪枪机框导柱进入弹膛螺旋槽时，两者之间冲击过大，造成枪机框速度损失严重的问题进行了研究分析，并对弹膛螺旋槽形状进行了优化设计.利用枪械射击试验验证了优化结果的可信性及有效性，得出以下主要结论：

① 通过某埋头弹枪实际射击试验，发现枪机框导柱与摆动弹膛螺旋槽相互作用时，枪机框速度损失较大，且存在弹膛摆动为枪机框反向加速的情况，根据以上两点情况，可知枪机框导柱进入弹膛螺旋槽时，对螺旋槽的冲击力较大；

② 在导柱对弹膛螺旋槽冲击力分析中，通过将理论轮廓线离散为点集的形式，可以依靠Hertz 接触理论计算出导柱在每个点上与弹膛螺旋槽之间的撞击力，从而检索出导柱与螺旋槽相互作用过程中的最大撞击力；

③ 通过选用5 次函数曲线为弹膛螺旋槽理论轮廓线展开线的形式，并用遗传算法优化弹膛螺旋槽理论轮廓线的具体形状，使导柱与螺旋槽之间的最大撞击力最小，即得到本文所需要的最优曲线.按照最优曲线形状重新加工弹膛螺旋槽，并做试验，得出导柱在与弹膛螺旋槽相互作用的整个过程中，枪机框速度损耗由优化前的30.3%降低到优化后的25.6%.并由仿真分析得出，导柱与弹膛之间的最大冲击力降低了57.73%，达到了优化目的.

本文在力学分析中选用了简化的接触模型，将枪机框导柱与弹膛螺旋槽之间的接触简化为点接触，这种简化是符合工程需求的[1].但实际上，导柱、螺旋槽壁面在啮合中两者相切，属于共轭曲面，共轭曲面之间的接触通常为线接触.在后续的研究中，笔者将建立更为精确的线接触模型，依靠“曲率分析”[7,14]等理论重新求解两者之间的接触力，并依此建立更加精确的优化模型以进行优化分析及计算.