收放伞绳对十字型伞静态气动特性影响的数值模拟研究

胡俊，于菲，于勇

（北京理工大学 宇航学院，北京 100081）

降落伞作为一种可展开式气动减速器，具有质量小、折叠体积小、价格便宜、阻力特性好等优点，被广泛应用于空投、航天器回收、新型武器等领域.

降落伞工作过程包括拉直、充气、减速和稳降，其中的拉直和充气阶段历时短、变形大，涉及几何非线性和材料非线性并存的流固耦合问题[1].降落伞的实验研究包括风洞实验、飞行实验等方法.如 LEVIN 等[2]通过风洞试验测量了5 种不同伞面形状的十字型伞的气动力以及俯仰力矩，并与空投实验数据进行了结果对比，得到不同形状、不同臂长比十字型伞的气动力规律.RENDER 等[3]、LUDTKE[4]、BRAUN等[5]主要对小型十字伞伞群进行了一系列风洞试验，研究了物伞连接绳长度和伞面之间系留绳长度对伞群系统气动力的影响，对2 种不同尺寸的伞群系统进行不同的雷诺数范围内的阻力测量，得出了伞群阻力系数与单伞阻力系数之间的关系式.NASA 兰利研究中心[6]多次采用飞行实验，对“行星进入降落伞计划”（planetary entry parachute program，PEPP）中不同构型的降落伞，进行有关稳定性、阻力性能和降落伞尾迹的研究.

随着计算机技术的发展，数值模拟也成为降落伞研究的一种手段.通过将稳定的降落伞视为刚体，模拟研究降落伞的气动特性和周围流场.如XUE等[7-8]采用CFD 方法针对探测器超声速降落伞系统进行了详细研究，观察了探测器尾流与伞前激波、探测器激波与伞前激波的气动干扰以及伞绳激波、风洞连杆激波对整体流场的影响情况.周彤等[9]、李尧尧等[10]也采用了CFD 的方法对伞-弹系统中的相关气动问题进行了研究.BARNHARDT 等[11]则采用分离涡模拟方法研究了NASA“火星科学实验室任务”相关的超声速降落伞系统，模拟了超声速来流下的探测器-降落伞系统，研究了前体探测器尾流对降落伞气动性能的影响，分析了尾流对伞衣压力、阻力的影响以及伞衣带底部有可能会出现部分坍塌的原因.

降落伞在稳定减速和稳定下降阶段时，将伞衣视为刚体是可行的，但是在降落伞的拉直和充气阶段，伞衣会出现结构大变形，不能再将伞衣视为刚体，此时数值模拟主要采用任意拉格朗日-欧拉（arbitrary Lagrangian-Eulerian，ALE）法.2011 年TUTT 等[12]首次采用ALE 方法模拟降落伞有限质量充气过程，结果验证了ALE 方法对开伞力、下降速度及降落伞呼吸频率有较好的预测，验证了ALE 流固耦合方法模拟有限质量开伞过程的可行性.GAO 等[13]采用ALE算法模拟了开缝伞的有限质量充气过程，用显式中心差分法求解了不可压缩流动的Navier-Stokes (N-S)方程，得到了伞衣变形过程、减速规律及开伞过载.

降落伞作为气动减速器，其主要作用是对载荷进行减速，避免载荷在到达落点时产生过大的冲击，从而达到保护载荷的作用.但传统的降落伞在运动过程中无法对物伞系统的运动状态进行主动调整.为了提高物伞系统落点的精准度，近年来开始出现主动控制降落伞的应用研究.通过伞绳的收放，改变伞面构型，从而影响改变伞面所受气动力，达到控制物伞系统运动状态的目的.

降落伞的主动控制最早由美国提出，运用于精确控制空投系统的轨迹控制.BERGERON 等[14-15]在十字型伞的其中一片伞臂上添加了扰流片，通过扰流片的关闭和打开改变伞衣内部的流场结构，使伞衣变形，达到改变降落伞气动性能的目的.FIELDS 等[16]通过在伞面安装驱动装置改变伞绳长度，控制降落伞的旋转或滑翔，根据空投实验数据开发四自由度及PID 控制模型，将着陆位置圆误差降低2～4 倍；李龙恩[17]通过动力学建模的方法，研究收放局部伞绳实现对圆形降落伞控制的可行性，发现收放局部伞绳能够实现对降落伞的主动控制.

有关学者对于降落伞主动控制的研究主要集中在实现伞绳收放的控制方法与控制装置等方面，但对于降落伞收缩伞绳产生的气动力规律没有系统地认识.掌握降落伞收缩伞绳之后的运动规律和气动力变化规律是实现降落伞主动控制应用的前提条件，同时也影响着发送调控指令的时间节点.不同伞绳收缩长度时降落伞的气动特性，尤其是侧向控制力的规律是降落伞主动控制成功应用的重要因素.本文以十字型降落伞为研究对象，建立收缩不同伞绳长度的降落伞无限质量充气的有限元模型，采用ALE流固耦合方法，对收缩不同伞绳长度时十字型伞的气动特性进行研究，为用十字型降落伞进行主动控制提供参考.

1 计算方法

1.1 ALE 算法

柔性降落伞在运动过程中和空气的相互作用具有强非线性时变的特点，两者的耦合是同时涉及几何非线性和材料非线性的瞬间大变形双向耦合问题.ALE 算法是一种基于罚函数的接触耦合算法，结合了拉格朗日算法（主要用于求解固体力学）和欧拉算法（主要用于求解流体力学）的优点，可以实现结构和流体的双向耦合.

1.2 控制方程

ALE 描述下的流体模型遵循Navier-Stokes 方程，其中包括连续性方程、动量守恒方程、能量守恒方程.

ALE 描述下的连续性（质量守恒）方程为

ALE 描述下的动量守恒方程为

ALE 描述下的能量守恒方程为

式中： ρ为流体密度；t为时间；vi为流体速度；wi为参考构型下网格点移动速度；bi为单位质量体力；e为单位质量内能； σij为应力张量，表达式为：

其中：p为流体压力； δij为克罗尼克函数； µ为流体动力黏度系数.

ALE 方法对固体域采用Lagrange 描述.降落伞的结构控制方程为

式中： ρs为降落伞织物密度；u为单元位移； σs为柯西应力张量；f为单元所受体积力；g为重力加速度.

降落伞伞衣采用不考虑厚度的二维薄壳结构，材料选择织物，伞衣织物的透气量与透过伞衣的流体速度呈二次多项式关系[18]：

式中： Δp为织物两侧压力差；e为织物厚度；a、b分别为黏性系数和惯性系数，均是关于多孔介质相对透气量 ε和空气动力黏度 µ的多项式.

1.3 流固耦合方法

建立伞衣结构网格和流体网格重叠的有限元模型，使用罚函数接触耦合算法实现力学参量的传递，在任意tn时间步内，追踪拉格朗日节点（从节点）穿透欧拉流体物质（主节点）的相对位移dn，则下一时刻迭代结果为：

式中：vrel为主从节点相对速度；主从节点速度为等参坐标变化后得到的某一流体质点速度vf；从节点速度为结构节点速度vs； Δt为时间步长.

2 算法验证

2.1 十字型伞几何结构

十字型降落伞主要包括伞衣和伞绳两部分，其中，伞衣部分是由5 片尺寸相同、材质相同的织物缝制而成，十字型伞的几何结构如图1 所示.L为伞长臂，W为伞短臂，Ls为伞绳长度.十字型伞的气动特性主要受其几何参数的影响，其中主要几何参数包括臂长比A=L/W和伞绳比Rs=Ls/L.

2.2 坐标系定义与受力分析

如图2 所示建立坐标系，伞绳节点作为坐标系原点O，来流方向为坐标系的+Z轴，与Z轴垂直的平面为XY平面，建立风轴坐标系OXYZ；以压力中心O′作为坐标系原点，伞轴所在直线OO′作为Z′轴，与Z′轴垂直的平面为X′Y′平面，建立体轴坐标系O′X′Y′Z′.

风轴坐标系Z轴与体轴坐标系Z′轴之间的夹角为 α.在风洞实验中，通过固定降落伞伞顶进行降落伞的静态气动特性研究，该夹角就是降落伞静态实验中的攻角.

图3 所示为降落伞的受力示意图.风轴坐标系中降落伞的气动力主要包括阻力FD和升力FL.体轴坐标系中，降落伞的主要受力为轴向力FT和法向力FN.

计算气动力系数时所用到的参考面积为十字型伞的名义面积S0，表达式[19]为：

2.3 验证结果

为验证ALE 方法在十字型降落伞研究中的适用性，以文献[20]中风洞试验的十字型降落伞为例，采用ALE 算法对对称十字型降落伞进行数值模拟，十字型降落伞的具体尺寸和计算条件如表1 所示.

表1 十字型降落伞的尺寸和来流条件[20]Tab.1 Parameters of cross parachute and flow condition [20]

采用上述降落伞尺寸，模拟了攻角为0°和15°时十字型伞由平面状态充气至稳定运动的过程，取计算稳定后的1～4 s 的轴向力数据，计算时间平均值，结果如图4 所示.

图4 风洞试验数据[20]和模拟数据对比Fig.4 Comparison of wind tunnel data [20] and simulation data

攻角为0°时采用数值方法计算出十字型伞的轴向力系数大小为0.822，风洞试验所得轴向力系数为0.8，两者误差约为2.75%；攻角为15°时数值计算出轴向力系数为0.765，风洞试验所得轴向力系数为0.712，两者误差约为7.4%.

综上所述，数值模拟计算与风洞试验数据误差小于10%，认为本文所使用的数值模拟方法适用于十字型降落伞模拟计算.

3 模型建立

3.1 几何模型

本文基于某火箭弹小角度迅捷转弯制定了一种十字型降落伞，具体几何尺寸如表2 所示.

表2 十字型降落伞的几何尺寸Tab.2 Geometric parameters of cross parachute

每个伞臂连接2 根伞绳，整个降落伞系统共有8 根伞绳.本文目的是研究十字型降落伞在稳定状态下的气动特性，对开伞过程不做精确要求，所以将降落伞的初始状态设置为十字形平面状态，见图1.

3.2 有限元模型

伞面结构为薄壳单元，对伞面进行正四边形网格划分，保证每个伞面网格的质量均等.伞绳结构采取离散梁单元，流场域采取固体单元.十字型伞的流场域采用直径为5L、高度为6L的圆柱形计算域，采用结构性网格划分，相关的有限元模型参数如表3所示.

表3 降落伞的有限元模型参数Tab.3 Finite element model parameters of parachute

流场域和伞面的网格划分如图5 所示.

图5 网格示意图Fig.5 Diagram of mesh

3.3 计算条件

如图6 所示，收缩伞臂A所连接的2 根伞绳，收缩长度定义为Δl=Ls-，单位为m，收缩比定义为δ=Δl/Ls.

图6 伞绳收缩示意图Fig.6 Diagram of suspension line retracting

来流速度为68 m/s，来流密度为1.205 kg/m3，当收缩长度 Δl为0、0.16、0.20、0.24、0.32、0.40 m 时，所对应的收缩比δ及其他计算条件如表4 所示.

表4 数值模拟计算条件Tab.4 Numerical simulation conditions

4 计算结果及分析

4.1 伞绳收缩长度对十字型伞气动特性的影响

通过伞绳的收缩，十字型降落伞由对称性几何构型变成非对称性几何构型，同时降落伞的气动力参数发生改变.

图7 所示为0°、5°、10°攻角时，十字型伞的瞬时阻力系数随时间的变化.

图7 不同收缩比十字型伞的阻力系数Fig.7 Drag coefficients of cross parachutes with different retraction ratios

选择计算稳定后的1～4 s 的数据，取时间平均值，计算得到平均阻力系数，如图8 所示.

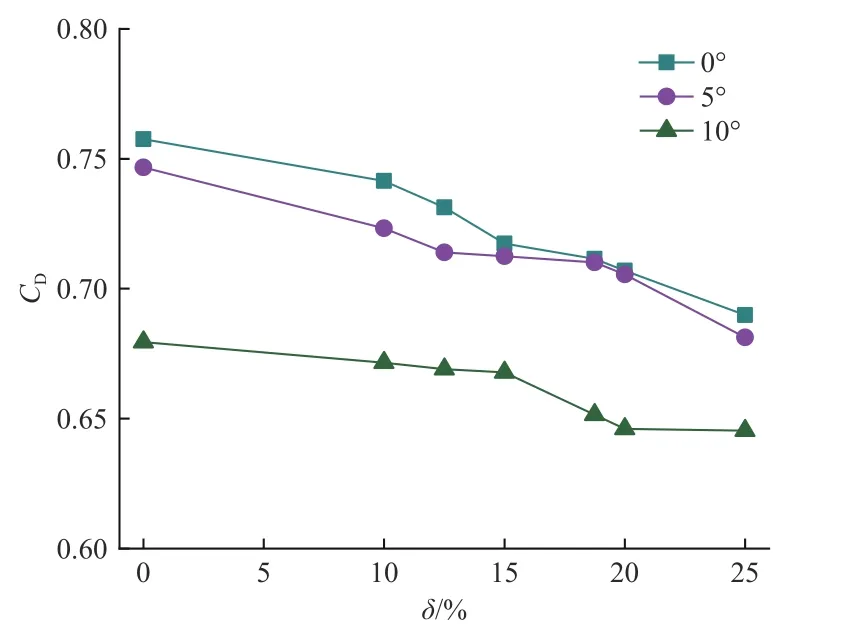
图8 平均阻力系数随收缩比 δ变化图Fig.8 Retraction ratio vs mean drag coefficient

从图中可以看出，十字型伞的平均阻力系数随伞绳收缩比 δ的增大而减小.降落伞的阻力系数主要受阻力面积的影响，而十字型伞的伞面构型相较于其他伞型，受同等数量的伞绳长度缩短的影响程度较大，所以伞绳收缩时，平均阻力系数的减小较为显著.

从图7(b)、7(c)可以看出，在5°、10°攻角时，伞绳收缩的十字型伞的瞬时阻力系数随时间有较为明显的波动.这是因为当十字伞处于非零攻角且伞绳同时收缩时，由于伞面的柔性，迎风面积会随着十字伞自旋发生变化，图9 中展示了当攻角为10°、收缩比δ=20.0%时，十字型伞发生自旋运动时，t1、t2时刻（如图7(c)中收缩比20%、攻角10°工况，选取某个周期中阻力系数最大和最小的2 个典型时刻）下，十字型伞的伞面状态.由图中可以明显看出，t1时刻伞面的迎风面积明显大于t2时刻的迎风面积.

图9 t1 时刻和t2 时刻的伞面状态 (收缩比δ=20.0%)δ=20.0%Fig.9 State of canopy at t1 and t2 (retracting ratio )

图10 所示为0°、5°、10°攻角时，十字型伞的瞬时升力系数随时间的变化.

图10 不同收缩比 δ时十字型伞的升力系数Fig.10 Lift coefficient of cross parachute vs retraction ratio δ

选择计算稳定后的1～4 s，取时间平均值，计算平均升力系数，如图11 所示.伞的平均升力系数基本没有影响.在5°和10°攻角时，伞绳收缩会引起平均升力系数的降低.

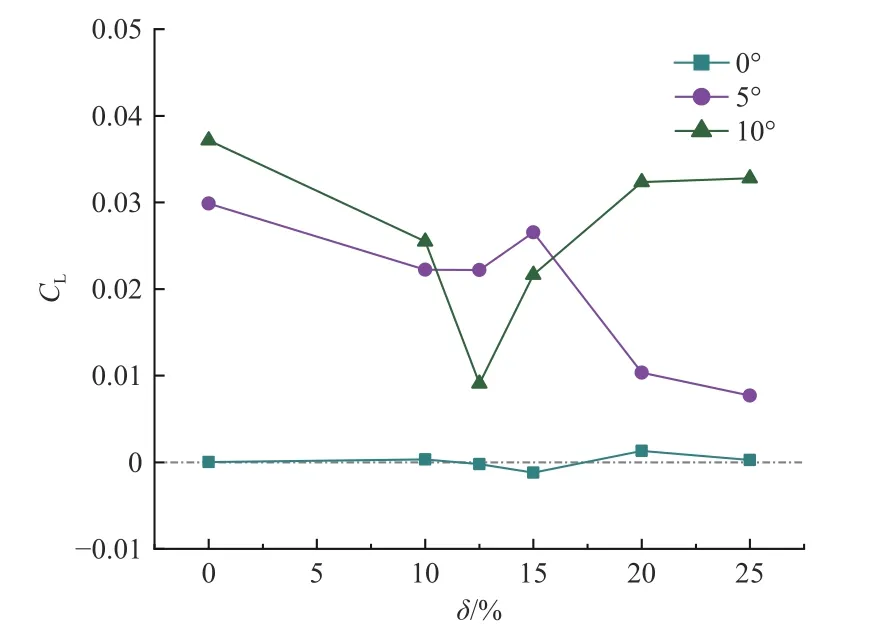
图11 平均升力系数随收缩比 δ变化图Fig.11 Retraction ratio δ vs mean lift coefficient

根据图10(a)可以看出，0°攻角时，瞬时升力随着自旋运动呈现出明显的周期性，升力的方向随着下拉伞臂A旋转到不同位置而发生变化；同时从不同收缩比的工况可以看出，十字型伞瞬时升力系数的峰值与伞绳收缩比 δ密切相关.

由图10(b)、10(c)所示，攻角为5°、10°时，升力系数受到攻角和收缩比 δ这2 个因素的共同影响.当伞绳收缩比 δ为0 时，升力主要受攻角影响，方向始终指向+X方向，并且升力为正值；当 δ不为0 时，升力除了受攻角影响之外，还包括来自伞绳收缩的影响.随着下拉伞臂A的旋转，如图12(b)、12(c)所示，伞臂A的位置从伞轴左侧运动至伞轴右侧，导致升力时刻发生变化.随着伞绳收缩比 δ的增加，瞬时升力系数的峰值增大，如t1时刻(在收缩比为20%、攻角

图12 收缩比δ=0 与δ=20.0%的伞面压力云图 (10°攻角)Fig.12 Pressure contour of canopy with δ=0 and δ=20.0% (angle of attack was 10°)

从图中可以看出，在0°攻角时，十字型伞的平均升力系数基本为0，伞绳收缩比 δ对0°攻角的十字型为10°工况，选取某个周期升力最大的典型时刻，如图10(c)所示).随着伞绳收缩比 δ的增加，瞬时升力系数的最小值减小.当 δ较大时，收缩伞绳对升力的影响大于攻角对升力的影响，瞬时升力系数最小值逐渐出现负值，如t2时刻(在收缩比为20%、攻角为10°工况，选取某个周期升力最小的典型时刻，如图10(c)所示).

当攻角为10°、收缩比δ=0 和δ=20.0%的t1、t2时刻，Y=0 平面的压力云图如图12 所示，速度矢量图如图13 所示.

图13 收缩比δ=0 与δ=20.0%的速度矢量图 (10°攻角)Fig.13 Velocity vector of canopy with δ=0 and δ=20.0% (angle of attack was 10°)

由图12 可以看出，在10°攻角、收缩比δ=0工况时，伞衣内部的压强关于伞轴非对称分布.在收缩比δ=20.0%工况时，t1时刻，收缩伞绳在伞轴左侧，加剧了伞面几何构型的非对称性，导致高压区向伞轴右侧产生了进一步的偏移，此时伞面受到的升力最大；t2时刻，收缩伞绳在伞轴的右侧，下拉伞臂A在来流的冲击下，出现伞面底边向内凹陷的现象，由于内凹伞面的阻挡，来流在A处发生绕流，如图13(c)所示，伞臂A内侧出现漩涡区，出现较为明显的低压区，而高压区出现在伞臂C内侧，如图12(c)所示，此时，伞面受到的升力最小，为负值.

5 结 论

本文对不同伞绳收缩比 δ的十字型降落伞进行了数值模拟研究，结果表明：

① 十字型降落伞的阻力系数随收缩比 δ的增大而减小.

② 由于十字伞存在自旋运动，下拉伞臂A的位置随着自旋发生改变，导致升力具有较强的时变特性.十字型伞瞬时升力峰值随收缩比 δ增大而增大.

本文的研究内容是十字型伞作为主动控制装置的基础性研究工作，后续将对收缩多根（超过2 根）伞绳以及不同伞绳收缩组合下引起的其他非对称构型对侧向气动力的影响进行研究，制定出合理的伞绳收缩策略，实现十字型伞对弹箭系统运动姿态的调控.