复杂结构内爆炸冲击波传播的大规模计算方法研究

王成，王雪桃，李涛，张志刚，孙伟福

（1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081；2.中煤科工集团重庆研究院有限公司，重庆 400039；3.煤矿灾害防控全国重点实验室，重庆 400039）

爆炸冲击波是矿井等复杂密闭建筑结构发生爆炸事故产生的主要灾害效应之一，冲击波不仅会造成人员伤亡，还会对周围结构及建筑物造成大规模破坏.空中自由场等开放空间发生爆炸事故时，由于爆炸冲击波未受任何约束，通常以指数形式快速衰减.然而，矿井巷道等密闭空间内爆炸产生的冲击波由于受到壁面等结构的约束作用，在其扩散过程中会发生多次的反射、折射等效应，并随之发生多次叠加作用，使得冲击波超压峰值较多且难以衰减至常压，在很大程度上提高了爆炸压力和能量.因此，爆炸冲击波在复杂地下密闭空间内的传播规律是矿井、巷道等制定防爆及抗爆安全的主要科学依据，在爆炸事故的快速应急响应及防护救援等过程中具有极其重要的理论意义和实际应用价值.

关于类似巷道、矿井等复杂密闭结构内的爆炸问题，陈海天等[1]、庞伟宾等[2-3]及其他研究者[4-6]通过实验对其进行了理论研究，并基于自由场爆炸冲击波压强预测公式，得到了直边墙拱形隧道、方形坑道、T 型坑道以及不同分叉角度的坑道内爆炸冲击波的衰减规律.但由于巷道在弯曲处和交叉处的冲击波流场分布极其复杂，理论研究无法对其传播过程进行直观的反映，所以仅通过实验对巷道内爆问题进行深入细致的研究存在许多实际困难.因此，近些年来数值模拟技术在结构内爆问题中得到了广泛应用.张奇[7]、屈康康等[8]及其他研究者们[9-18]利用Autodyn、LS-DYNA 等有限元软件对长直坑道、L 形坑道、S 形坑道、分叉管道、变径管道等不同形状巷道内的冲击波传播规律进行了研究.樊保龙等[19]、王成等[20]对密闭巷道内瓦斯的爆炸过程进行了数值分析.胡洋等[21]、宋诗谦等[22]、张晓伟等[23]及吴文溢等[24]对密闭空间内TNT 爆炸效应进行了数值模拟分析.张学博等[25]提出了冲击波传播的分段接力数值模拟法，并实现了矿井大尺度爆炸问题的二维模型模拟冲击波传播.杨科之等[26]通过自主计算程序对简单巷道内爆流场进行了数值计算，并得出冲击波在巷道内衰减的计算公式，但是Autodyn 等商业软件无法对炸药放置于地面或近壁面的爆炸过程进行高效计算，也无法对近、中场的爆炸问题进行准确计算[27].另外，目前现有的自主编制爆炸流场的程序更多地是对简单、小尺寸的爆炸问题进行计算，若对大尺寸的复杂密闭空间结构进行数值模拟，则存在一定的难度和局限性.对于类似于地下矿井等大尺度的复杂密闭空间结构，若在计算时整体计算域采用较粗的网格，则会导致计算结果不准确；若全流场采用较为精细的网格尺寸，则会导致由于网格数目过多而无法正常计算，即使利用高性能的计算设备和大规模的并行处理器，也会浪费大量的内存和计算资源.

针对大尺寸复杂结构内爆数值计算浪费大量计算资源的问题，在此提出了一种基于数据流的分块续算方法，并通过文献实验结果以及标准模型算例验证了该计算方法的准确性和有效性，实现了复杂地下密闭空间内爆问题的大规模、高效率、高精度数值模拟.同时，以复杂地下密闭空间结构中的爆炸问题为研究对象，采用基于数据流的分块续算方法对一个包含长方体形工房、圆柱形泄压洞的复杂结构内的爆炸冲击波传播过程进行了数值模拟，并给出了冲击波在巷道内的传播规律.

1 数学模型及算法

1.1 数学模型

由于炸药在爆轰传播过程中，冲击波的传播速度很快，因此分子扩散、热传导及黏性效应在模型计算中可以忽略.控制方程组为由质量守恒、动量守恒和能量守恒组成的非定常可压缩三维Euler 方程组：

式中： ρ为密度；p为压强；u、v、w为速度矢量分量；E为单位质量的总能量，是单位质量的比内能e与动能的总和，满足

为了使上述控制方程组封闭，需引入描述压强、密度和比内能之间关系的状态方程.爆轰产物采用JWL 状态方程，空气介质采用理想气体状态方程.

JWL 状态方程为：

式中：p为压强； ρ为密度；e为单位质量的比内能；A、B、R1、R2、 ω 和 ρ0为爆轰产物的材料常数.

理想气体状态方程为：

式中：p为压强； ρ为密度；e为比内能； γ为多方气体指数，对于空气 γ一般取为1.4.

1.2 数值计算方法

在复杂结构内爆炸冲击波流场的数值模拟过程中，为确保冲击波的追踪精度，采用5 阶WENO（weighted essentially non-oscillatory）高精度有限差分格式[28]进行空间离散，采用3 阶精度的TVD Runge-Kutta 方法进行时间离散.针对多介质爆炸流场问题，采用RGFM（real ghost fluid method）[29]和 Level-set[30-31]相结合的物质界面处理方法，通过Level-set 方法对界面进行隐式追踪，通过求解法向黎曼问题确定物质界面附近流场相互接触作用之后的流动状态，并利用RGFM 方法对界面处流场进行处理，实现了复杂地下密闭空间结构内爆轰产物及爆炸冲击波传播过程的高精度数值模拟.另外，通过采用一种基于WENO格式的自适应扩大计算域高精度算法[32]，提高了多介质界面追踪与处理的精度和分辨率，加快了计算效率.在此基础上，引入MPI（message passing interface）并行计算方法，对自适应扩大计算域进行并行计算，即可实现高精度大规模爆炸问题的数值模拟.

在该大规模计算方法中，复杂结构内爆炸问题的数值模型一般包括两部分区域：计算域和障碍物区域Ωobstacle，如图1 所示.其中，在计算域中设置炸药区域ΩTNT、空气域Ωair两种介质以及刚性壁面区域，爆轰产物采用JWL 状态方程计算，空气采用理想气体状态方程.障碍物区域不参与计算，但由于矿井、巷道等地下空间的壁面一般为钢筋混凝土墙，所以在障碍物与空气/爆轰产物的交界处给定固壁无滑移边界条件，用于模拟刚性壁面的反射过程.

2 分块续算方法

由于地下空间或矿井等大规模复杂结构爆炸问题的数值研究都是百米、千米量级，而炸药爆炸形成的爆轰波阵面厚度通常在微米量级；另外，三维的爆炸问题存在时间和空间上的多尺度特性，若计算区域采用粗网格划分会带来较大的累积误差，导致计算结果不准确甚至不收敛；若采用精细网格则只能对小尺寸的简单结构进行模拟，大规模复杂密闭空间结构由于网格数目巨大，即使采用并行技术也很难满足对其全尺寸快速计算的需求，对其进行全尺寸网格划分更会浪费大量的CPU 计算资源.以图2所示的二维结构的爆炸问题为例，若对其进行全尺寸计算时需要72 个CPU 并行计算，且其中有36 个处于障碍物区域不参与计算（图中阴影区域所示），极大地浪费了计算资源，如图2（a）所示.为了减少大量计算资源的浪费，提高计算效率，实现对大规模复杂结构内爆炸问题的全流场数值模拟，提出了一种基于数据流的分块续算方法，通过合理划分模型并对每个部分进行单独计算可对CPU 进行有效利用，如图2（b）所示.对该二维结构模型利用分块续算方法计算时，共需要44 个CPU 但只有6 个处于障碍物区域，与全尺寸计算方法相比，节约了39%的CPU核数，有效利用了计算域，减少了计算资源的浪费.另外，若全尺寸计算需72n核时，则分块续算共需22n核时，计算核时相比于全尺寸计算节约了69%.若以三维结构来看，全尺寸计算浪费的CPU 计算资源更多，因此与全尺寸计算相比，数据流分块续算方法极大地减少了计算资源的浪费，对复杂结构进行合理划分即可有效实现其内爆流场的数值模拟.

以下简要叙述数据流分块续算方法的流程：

① 划分模型.

在对矿井、巷道等复杂地下空间大尺度爆炸问题进行模拟时，可根据实际情况将计算模型进行简化，并根据模型几何形状和爆炸流场的流体动力学特征将模型各部分进行合理划分，即将整个计算模型划分为若干部分（PART-i，i=1,2,3,···），使得在对每个部分进行数值计算时尽可能少地浪费计算资源.

② 数据储存.

通常情况下，将放置炸药的模型部分划分为PART-1 对其先进行计算.首先根据具体的爆炸流场尺度以及计算资源，确定该部分的计算域尺寸、每个方向的CPU 数以及每个分区中的网格数，并给定计算域各CPU 的序号.另外，在PART-1 模型的出口处设置一个数据储存区域，记为Ω，如图2（b）所示.在计算若干时间步后，该部分模型计算域中的爆炸冲击波向外传播，当冲击波传播至PART-1 中Ω区域的80%～85%时，程序停止计算并将这一时刻Ω区域内各CPU 所有计算网格点的物理量（包括密度、3个方向的速度、总能量、压力等）保存至文件中，即数据储存.

③ 数据赋值.

在进行下一部分即PART-2 的计算时，同样先确定该部分的计算域尺寸，并按PART-1 的网格大小对其进行网格划分，使得相邻PART 间能够进行“映射”数据流的传递.在开始计算前，先更新时间步，让两部分程序的时间同步.另外，在PART-2 中设置一块与PART-1 完全重叠的区域Ω，在计算该部分模型时，将上一部分模型PART-1 保存的区域Ω的数据作为该部分的初始条件，在开始计算时读入此文件并重新启动程序，将区域Ω内各CPU 所有网格点的物理量直接映射在该部分区域Ω内相对应的计算网格点上，然后继续求解欧拉方程进行计算，即数据赋值.若进行计算的整个大规模模型被划分为很多部分，则根据流场中爆炸冲击波的传播过程对所有PART依次进行数据储存、数据赋值的数据流传递，即可实现对整个模型的爆炸流场进行数值模拟.

分块续算方法由于在相邻PART 间分割处都会设置重叠区域，且各部分模型之间是通过数据储存、数据赋值的方式来进行数据流传递的，因此，相对于全尺寸计算，这种计算方法增加了一定的计算量.但是，相邻PART 间的这种直接映射的数据流传递方式也保证了数据的完整性，区域Ω在一定程度上可以代表上一个PART 计算得到的结果，使得接续计算时产生的误差可以忽略（下文对此进行了验证）.更为重要的是，分块续算方法解决了大尺度复杂结构由于网格数目过大而无法计算的难题，更解决了计算资源的大量浪费问题，实现了复杂地下密闭空间内爆炸冲击波传播的大规模数值模拟，在矿井、巷道等复杂地下空间的防爆抗爆设计中具有广阔的应用前景.

3 验证性算例

3.1 计算方法验证

为了验证该计算方法与其数值计算结果的准确性，结合文献[6]对方形坑道内爆炸冲击波传播的实验结果，设计了两端开口的TNT 方形坑道内爆的计算模型，并利用该计算方法对其爆炸流场中的冲击波衰减过程进行数值计算.该计算模型示意图如图3所示，方形坑道截面长×宽为1.2 m×1.8 m，坑道总长为41 m.圆柱形TNT 装药的密度为1.57 g/cm3，质量为3.25 kg.柱状装药距离地面0.9 m，且悬挂于距离坑道端面5 m 的位置.在坑道一侧壁面的爆心所在截面上分别距离爆心6、10、16、20 、28、36 m 处设置超压测点，其布置如图3 所示.

图3 方形坑道数值计算测点布置示意图Fig.3 Diagram of measuring point layout for numerical calculation of square tunnel

表1 列出了文献[5]所得实验值以及数值模拟所得典型测点处的超压峰值.从表中可以看出，20 m处冲击波超压的数值计算结果与实验结果基本一致，而越靠近爆炸中心的测点，超压峰值的偏差相对越大.因为在实验中距离炸药越近的地方冲击波压力越高，传感器受震动会产生较多杂信号，而且灵敏度（分辨率）不同，会影响读数.但总体而言，利用该数值计算方法预测的峰值压力与实验所测得的压力值基本一致，相对误差在9.55%以内，证明该计算方法能够较为准确地预测结构内爆问题.

表1 典型测点处的文献实验及数值模拟超压峰值Tab.1 Literature experiments and numerical simulations of overpressure peaks at typical measurement points

3.2 分块续算方法验证

由于数据流分块续算方法在相邻PART 间用于“数据储存、数据赋值”的Ω区域只保存了PART-i中爆炸冲击波的主要流场数据，实际上Ω区域以外的爆炸流场对后续冲击波的传播也有一定的影响.为了研究Ω区域保存的流场数据能否作为下一部分PART-（i+1）的初始条件，实现PART 之间的冲击波续算过程，设计了如图4 所示的标准模型算例对分块续算方法的准确性进行了验证.

图4 标准模型算例示意图Fig.4 Schematic diagram of standard model calculation example

该计算模型由一个4 m×4 m×3 m 的长方体和半径为1 m、长10 m 的管道组成，长方体内放置一块药量为50 kg 的TNT 正方体状装药，位于距离地面高0.5 m 处.整个计算域有两种介质：空气介质和TNT炸药，空气介质采用理想气体状态方程，TNT 炸药采用JWL 状态方程.另外，在计算域长管道中心轴线方向每隔1 m 设置一个冲击波超压峰值测点，用于记录冲击波超压在管道内随距离的衰减过程.

为验证数据流分块续算方法的准确性，对该计算模型内的爆炸问题进行两次数值计算即全尺寸计算和分块续算.全尺寸计算时，计算模型不进行拆分直接对整个计算域划分网格进行计算，如图4 所示，网格尺寸dx=dy=dz=0.01 m，网格总数约为2.94 亿，采用600 个CPU 并行计算，总的计算时长为19 h；分块续算时，将整个计算模型划分为PART-1 和PART-2两部分，并在PART-1 和PART-2 中分别设置一个长为2 m 的区域Ω，用于接续计算时数据流的传递，如图4（b）所示.续算时，网格尺寸不变，网格总数约为1.17 亿，共采用240 个CPU 并行计算，总的计算时长为8.5 h 左右.与全尺寸计算方法相比，分步续算方法节约了60.00%的CPU 核数，极大地减少了计算资源的浪费；另外，计算时长相比于全尺寸计算降低了55.26%左右，即分步续算方法在给定算例下相比于普通全尺寸计算，节约了88.68%的计算核时，极大地提高了计算效率.

表2 列出了全尺寸计算和分块续算得到的管道内典型测点处冲击波的超压峰值.可见分块续算得到的超压峰值与全尺寸计算时的基本一致，相对误差在0.33%以内.表明分块续算方法可实现基于数据流的数据传递，并能够保证数据在传递过程中的准确性.另外，对于复杂地下密闭空间等大规模结构，分块续算方法可以有效利用计算资源，节约计算时长，提高计算效率，实现爆炸流场中冲击波传播的大规模、高效率、高精度数值模拟.

表2 全尺寸计算和分块续算时典型测点处的超压峰值Tab.2 Peak overpressure at typical measuring points during full-scale calculation and block continuation

4 爆炸冲击波在复杂结构中的数值模拟

4.1 计算模型设置

针对复杂地下密闭空间结构中的爆炸问题，采用上文提出的基于数据流的分块续算方法，设计了一个包含长方体型工房及圆柱形泄压洞的大规模复杂结构对爆炸流场中的冲击波传播及衰减过程进行数值模拟，其计算模型示意图如图5 所示.

图5 大规模复杂结构计算模型示意图Fig.5 Diagram of large-scale complex structure calculation model

整个计算模型由工房、泄压洞A、B、C及泄压洞B和C出口的自由场区域组成，工房内放置一块质量为392 kg 的方形炸药，TNT 装药密度为1.58 g/cm3.其中，工房长×宽×高为14 m×5 m×5 m，泄压洞A和B的直径均为2 m，泄压洞C直径为1 m.泄压洞A长为10.5 m，泄压洞B包括7 m 的水平直段部分和15 m 的向上倾斜45°部分，泄压洞C长为25 m，整个模型的壁面都设置为固壁无滑移边界条件.另外，在泄压洞B和C的出口处分别设置一块4 m×4 m×2 m及16 m×8 m×2 m 的自由场区域，该部分边界条件设置为无反射出流.由于该计算模型较为复杂，为了减少计算资源的浪费，根据模型具体几何形状特征将其划分为6 个部分（PART-1、PART-2、PART-3.1、PART-3.2、PART-4.1、PART-4.2），并利用基于数据流的分块续算方法对其爆炸流场进行数值计算，如图6 所示.在该计算模型中，用于数据储存、数据赋值的Ω区域（即①～⑤区域）设置为1.6 m 长，整个模型各PART 间数据流的传递过程如图6 所示.

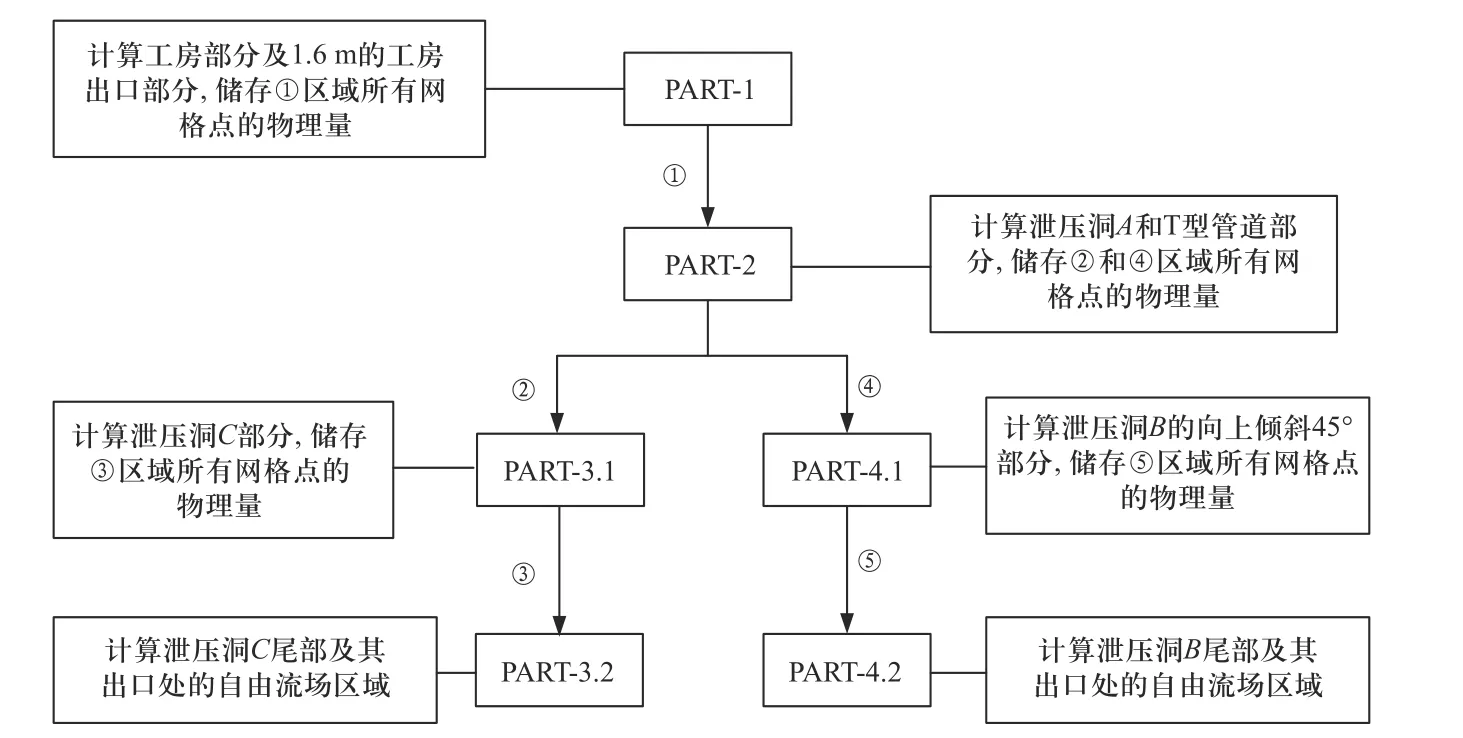
图6 数据流传递过程示意图Fig.6 Diagram of data flow transmission process

4.2 计算结果及分析

4.2.1 工房内部及工房出口处的冲击波传播规律

在工房内前后左右每个侧壁面的三等分点处分别设置2 个测点，其高度与炸药中心平齐，监测每个测点处的超压-时间曲线.通过数值计算可以发现，距离炸药最近的测点2、4 处的反射超压高达281.1 MPa，主要是由于高压冲击波直接撞击至壁面处形成反射波（如图7（b）所示），而在撞击壁面后冲击波在向外传播的同时压力快速衰减，因此测点1、3 处的超压峰值仅有29 MPa.

图7 PART-1 典型时刻压力云图Fig.7 Pressure distributions at typical time of PART-1

在1.030 ms 时，冲击波传播至泄压洞A内，由于工房与泄压洞A的交汇处存在T 字型拐角，致使此处产生极强的稀疏效应，密度与压强均接近于0，如图7（c）所示；冲击波在1.333 6 ms 时传播至泄压洞A右侧壁面，并在1.650 ms 时刻从右侧反射至管道中心轴线区域，因此使得泄压洞A始段约0.8、1.0 m 处的压力并不高，反而在泄压洞A约1.2～1.6 m 处的压力升高.在2.084、2.677 ms 时冲击波传播至工房右、左两侧壁面，并产生较高压力的反射波，分别高达54、45 MPa.

4.2.2 泄压洞A内部冲击波衰减规律

图8 给出了泄压洞A内部冲击波超压峰值随距离的衰减规律.在泄压洞A入口0 m 处，管道内中心轴线的超压峰值为9.78 MPa，随后爆炸冲击波以波动衰减的趋势逐渐减小，经过约10 m 长的泄压洞A后，冲击波波动衰减至约1.2 MPa 左右，与入口处相比降低了约88%.因为冲击波从工房传播出来时并不是平面波，从而导致冲击波在泄压洞内的壁面上来回反射，因此在泄压洞A内部的冲击波并不像空中自由场爆炸一样随着爆距的增加而快速衰减，而是以波动衰减的趋势逐渐降低，其波动衰减过程如图9（a）～9（d）所示.

图8 泄压洞A 内超压峰值衰减过程Fig.8 Attenuation process of overpressure peak in pressure relief tunnel A

图9 PART-2 典型时刻冲击波压力云图Fig.9 Pressure distributions at typical time of PART-2

4.2.3 泄压洞A、B、C交汇处T 型通道冲击波传播规律

由图9 可以看出，冲击波在约7.424 0 ms 时刻传播至泄压洞A侧R15 圆弧处，在9.268 4 ms 时撞击至泄压洞B侧R15 圆弧处，并产生较高反射压力，此后，该反射冲击波向泄压洞A、B和泄压洞C内传播，使得T 型区域的超压峰值有一定程度的升高.

由于冲击波在T 型区域处进行无规则反射，致使该区域超压较不稳定，为研究冲击波在T 型通道处的分流情况，此处取距离三管道中心轴线交点2 m 处的测点进行冲击波分流分析.通过读取相关测点处的超压峰值可知，泄压洞A内距离交点2 m处的超压峰值为1.39 MPa，泄压洞B的超压峰值为0.93 MPa，泄压洞C的超压峰值为0.89 MPa.即在T型通道分流处，与泄压洞A同等直径的泄压洞B的冲击波超压峰值约占分流前的67%，而呈直角且直径只有泄压洞A1/2 的泄压洞C的超压峰值约占分流前的64%.由此可见，分流时管道间采用直角交汇和缩小管道直径在一定程度上有利于冲击波超压的衰减.

4.2.4 泄压洞B和C内部冲击波衰减规律

从T 型区域开始，随着冲击波向外传播，泄压洞C内的冲击波超压值出现了明显减小，其衰减过程如图10（b）所示.冲击波超压峰值从泄压洞C内0 m的1.22 MPa 衰减至24 m 处的0.19 MPa，降低了84%，且其衰减速度逐渐减慢.由于泄压洞C前端部分位于T 型区域内，因此冲击波在0～3 m 范围内有一定的反射，超压峰值有所升高，在2.6 m 处达到最高值1.8 MPa.距离16 m 处开始波动衰减消失，超压峰值以缓慢的速度逐渐降低，说明在泄压洞C内16 m 左右, 冲击波经过多次壁面反射后已基本形成平面波.

图10 泄压洞B 和C 内部超压峰值衰减规律Fig.10 Attenuation law of overpressure peak inside relief tunnels B and C

冲击波于T 型通道分流后，在泄压洞B内经过7 m的水平直段及15 m 的向上倾斜45°部分的传播，其在斜段部分的衰减过程如图10（a）所示.爆炸冲击波的超压峰值从斜坡起始处的0.82 MPa 衰减至15 m处的0.20 MPa，降低了76%，而且其衰减速度逐渐减慢.同样，冲击波在斜坡管道内传播时，其超压峰值也是一个波动衰减的过程.

4.2.5 泄压洞B和C出口自由场区域冲击波衰减规律

泄压洞B和C外部自由场区域冲击波超压峰值测点的分布示意图如图11（a）和11（b）所示，其所对应的超压峰值分别如图11（c）和11（d）所示，可以看出，与管道内冲击波衰减规律不同，冲击波在自由场区域是持续衰减的，且其衰减速度比较快.爆炸冲击波从泄压内传出后，分别于1 m 和5 m 处“整合”为平面波.

图11 泄压洞出口测点分布及超压衰减过程Fig.11 Distribution of measuring points and the process of overpressure attenuation

4.3 Ω 区域取值对数值计算结果的影响

上述采用基于数据流的分块续算方法对爆炸冲击波在复杂结构内的传播过程进行了数值计算，为了在一定程度上能够减少计算量，用于数据储存、数据赋予的Ω区域不宜取得过大.上述计算模型中用于数据传递的Ω区域取值为1.6 m，在此通过对Ω区域进行适当的扩大，研究Ω区域的取值对分块续算结果的影响大小，进而验证数据流分块续算方法的准确性.

选用PART-3.1 和PART-3.2 两部分模型，对Ω区域的取值对计算结果的影响进行研究.用于数据传递的Ω区域扩大为原来的3 倍，即在计算PART-3.1 时，保存所有物理量的区域③由原来的1.6 m 扩大为4.8 m，在 PART-3.2 中也设置一块与PART-3.1中区域③重叠的区域③.图12 给出了Ω区域为1.6 m 和4.8 m 时，泄压洞C出口区域超压峰值衰减曲线比较图.由图中对比结果可以看出，冲击波在轴线方向、左斜及右斜方向的超压峰值衰减过程基本一致，因此，对上述大规模复杂结构进行分块续算时，进行数据传递的Ω区域取为1.6 m 是合理的，对整体爆炸流场的数值计算结果影响极小.

图12 Ω 区域为1.6 m 和4.8 m 时泄压洞C 出口区域超压峰值衰减过程比较Fig.12 Comparison of peak overpressure at outlet of pressure relief tunnel C when Ω is 1.6 m and 4.8 m

5 结 论

①提出了一种基于数据流的可计算复杂地下密闭空间内爆炸问题的分块续算方法，解决了计算资源的大量浪费问题，实现了复杂地下密闭空间内爆炸冲击波传播的大规模、高效率、高精度数值模拟，并利用典型实验与标准模型算例验证了该方法的准确性与有效性.

②利用该方法对一个包含长方体型工房和圆柱形泄压洞的大规模复杂结构内的爆炸问题进行了数值模拟，结果表明：冲击波在泄压洞内是以“波动”衰减的趋势逐渐减小的，且其衰减速度比在自由场的衰减慢；T 型分流处管道间采用直角交汇或缩小管道直径在一定程度上有利于冲击波超压的衰减.该方法在地下空间等大尺度复杂结构的防爆抗爆设计中具有广泛的应用前景.

③在此提出的数据流分块续算方法虽解决了计算资源的大量浪费问题，但是用于数据流传递的Ω区域只保存了爆炸冲击波的主要流场数据，实际上Ω区域以外的爆炸流场对后续冲击波的传播也有一定的影响.然而以上算例中将Ω区域的边界条件一律设置为固壁无滑移边界条件进行计算，在下一步研究中，需要优化对其边界条件的处理，使其更接近于真实流场中爆炸冲击波的传播.