基于参数化降阶模型的非线性气动弹性高效分析

陆召严，肖天航，常亮，邓双厚，付碧红，高海云

（1.中国科学院微小卫星创新研究院，上海 201304；2.南京航空航天大学 航空学院，江苏，南京 210016）

超声速和亚声速共存的跨声速流动的复杂强烈的非线性现象使得耦合非定常计算流体动力学(computational fluid dynamics，CFD)方法和结构运动方程的高精度计算气动弹性方法（computational aeroelasticity, CAE）成为跨声速颤振分析的重要手段[1].但随着计算精度的要求越来越高，计算模型越来越复杂，CAE 方法计算耗费巨大且难以应用于控制模型综合、多变量优化、稳定性预测和实时仿真等多学科设计领域的缺点日益突出[2-4].因此Dowell、NASA 的Silva 等为代表的气动弹性领域的学者们提出基于CFD 数值模型构造非定常流场降阶模型（reducedorder model, ROM）的思想[5]，旨在以远少于原数值模型的阶数和计算耗费提供系统主要动力学特征较精确的数学描述，同时可以方便研究者解释系统动力学特征.目前应用于流固耦合系统中非定常流场的ROM 主要有三类：子空间投影模型、代理模型和系统辨识模型[6-7].这些方法能够较好地模拟流场运动细节并具有较强的非线性，不仅可以用于非线性气动弹性问题研究, 也可以在流动预测与控制发挥巨大的作用，具有广泛的应用前景，成为当前最受关注和最有前途的降阶模型方法.

这些降阶模型都不同程度上有效地捕捉到流场的运动细节，有的甚至也可以捕捉模拟由于激波振动或者流体分离产生的非线性现象，但其构建的降阶模型只有在单一的构建模型对应的流场条件下才有效，对流场条件非常敏感，并不能适用于与系统参数、初始条件等密切相关的问题，因此高效地适合大飞行范围甚至全飞行范围的降阶模型一直是高效数值模拟领域的迫切需求.为了实现这个目的，大量研究人员基于Volterra 级数辨识方法拓展了其对变化的流场条件的应用领域，把流场计算条件如马赫数、攻角等作为其核函数的参数化变量应用于辨识过程，构建适用于参数化的气动弹性问题的降阶模型[8-12].此外，许多学者基于本征正交分解（proper orthogonal decomposition，POD）降阶模型构建了许多改进的算法来满足参数变化的需要，包括如全局POD 方法、局部POD 方法、自适应POD 方法等[13-14].虽然许多研究人员针对POD 降阶方法进行了降级模型的参数变化适应性研究，但从理论上并不支持得到的新POD 模态是否是该参数下的最优逼近，因此许多方法在参数域上缺乏鲁棒性.例如近年来提出的基于Grassmann 流形插值方法自适应POD 方法[15-16]，虽然在处理参数鲁棒性问题上取得了较好结果，但流形切空间具有局域性，其计算结果只有在参考点的领域内才是有效的，因此在大范围参数域内存在局限性.

综上所述，本文提出了一种适用于跨声速范围内对流场参数条件敏感的非线性气动弹性问题研究中高效计算多个流场条件下非定常流场数据的参数化降阶模型.该模型使用基于Grassmann 流场模态插值方法计算目标流场条件下的模态，使用加入流场参数影响的非线性系统辨识方法计算目标运动时的模态系数，解决了由于跨声速范围内流体变化的复杂性导致跨声速非线性气动弹性分析需要计算多个流场参数情况下的时域求解方程而耗费大量计算资源的问题，并成功应用于典型颤振模型的多流场参数变化时的颤振边界计算，验证其具有很高的计算效率和精度.

1 基于非线性系统辨识的非定常气动力降阶模型构建

基于非线性系统辨识和模态分析方法的降阶模型的构建过程可以归纳为4 个步骤：

①选择合适的训练信号作为外部激励，使用基于URANS 的非定常流场计算程序计算得到机翼表面随时间变化的压力系数数据.

②使用POD 模态分析方法对得到的非定常数据进行处理，得到分解的模态数据和模态系数.

③使用激励信号作为输入，模态系数作为输出，结合局部线性神经模糊模型对系统进行训练辨识，得到降阶模型.

基于LOLIMOT/POD 模型构建的降阶模型可以归结为系统辨识的降阶模型，根据输入输出信号建立基于局部线性模糊模型的数据关系，从而表示非线性流体计算模型的本质特征.在给定了输入和输出数据，选取了LOLIMOT 模型之后，根据判断准则对数据进行处理得到最优的模型参数就是模型的辨识过程.在LOLIMOT 模型中，系统的输入定义为模态坐标q，即激励信号，输出定义为POD 模态分析的模态系数（i=1,2,···,r为模态数，上标表示系统的预测输出，无上标表示真实的值），其训练模型的关系可以定义为

式中：k表示当前时间步，k-i表示向前i个时间步；M、N分别为输入和输出的延迟阶数.模型的辨识过程就是找到最优的输入空间划分方案并求出其对应的系数，最后保存并应用于后面的应用模块.

④使用目标激励信号和训练完的降阶模型得到目标运动中结构体的POD 模态系数，然后重组得到所需的流场数据.

目标运动的流场数据计算由三个部分组成，分别为稳态流场数据A、模态系数B和模态数据.稳态流场数据表示在给定的流场条件下得到的流场数据，包括给定的马赫数和攻角，其同样可以使用训练完成的降阶模型计算得到.动态的模态系数的计算由目标激励在降阶模型的输出中得到，从而结合POD模态分析中保存的模态结构数据组合重构目标运动下的流场数据，实现流场的快速计算.

图1 给出了基于非线性系统辨识和模态分析方法的降阶模型的创建流程图.整个流程分为系统辨识的训练模块和目标信号的非定常气动力的计算模块.

图1 流场参数不变降阶模型的构建Fig.1 Construction of reduced order model with no change of parameter

2 基于Grassmann 流形插值方法的变流场参数降阶模型

对于POD 模态对应的模态系数随马赫数变化的计算需要用到构建单一马赫数下气动力计算降阶模型中的非线性系统辨识方法，即用LOLIMOT 方法构建非线性系统的输入和输出的关系.不同于降阶模型中只关注外部激励信号和模态系数之间的关系，在参数变化的情况下需要加入流场参数的影响，例如，计算未知马赫数情况下的POD 模态系数，需要在外部激励信号作为输入的基础上，同时加入马赫数作为输入以保证考虑了马赫数参数变化的影响，然后建立非线性系统，使用LOLIMOT 算法进行辨识.

对于POD 的模态基函数，任意数目的POD 模态矩阵以及任意数目的操作点包含的物理参数量都可以通过基于Grassmann 流形的POD 插值方法构造新的操作点所对应的POD 模态矩阵.首先，对给定的NR个模态基矩阵进行处理，从中选取合适的矩阵对应的流形中的点作为参考点，即初始点S0，同时使用两点插值方法构建参考点和其他点之间的测地线路径函数.然后，在切空间内对每一条路径函数在初始点的导数进行插值，得到所需参数的操作点对应的表示矩阵，所用的插值方法取决于操作点空间包含的物理量的个数，比如一个可以使用Lagrangian 插值，多个参数使用多维插值方法等.最后，使用操作点对应的表示矩阵得到流形中新的测地线路径函数，从而求出所需的POD 模态矩阵.

使用Grassmann流形的插值方法构造的新的快照矩阵记为，对应的操作点记为λNR，流形上的点记为SNR.首先选取为参考点S0，基于切空间的标准的多点Grassmann 插值方法可以得到快照矩阵在切空间中随参数变化的表达式为

然后给定合适的迭代步长保证其在参考点的足够小的领域内，由流形插值方法得到λ0+Δλ处的系统快照矩阵，并重新作为新的参考点，逐步迭代可以得到所需参数处的快照矩阵，然后使用POD 方法，求得所需的降阶模态.

这样，使用非线性系统辨识方法就可以在已知的流场参数调节下计算得到未知的流场模态系数，对运动结构进行高效的非定常流场的模态进行计算，耦合模态插值方法不仅可以高效地计算机翼等结构的总体气动力特征，还可以高效地研究在运动结构表面的流场数据分布.非线性气动弹性的参数化降阶模型求解和构建过程如图2 所示.

图2 流场参数变化降阶模型的构建Fig.2 Construction of reduced order model with change of parameter

3 计算结果分析

3.1 三维机翼非定常简谐运动流场求解

三维LANN 机翼模型辨识数据由基于URANS的流体计算程序计算得到，计算网格包含130 万个节点，320 万个网格单元，计算域为以展长为单位长度1，设置为10×5×8（如图3 所示）.计算流场条件设置Ma=0.62,0.82，基于平均气动弦长的计算雷诺数为Re=5.43×106.计算的时间步长设置为5×10-4s，计算总的时间步为2 000 步，湍流模型选择S-A 模型.输入的激励信号为机翼的俯仰运动导致的攻角变化，其控制方程为α=α0+αˆ，其中 αˆ为扫频信号，其频率为20～50 Hz，幅值为2°，覆盖了所需模拟的俯仰运动的攻角变化范围和振动频率，保证可以得到明显的激波移动现象，初始幅值α0=0.6°，运动的旋转轴为65%根部弦长的位置[17-18].

图3 LANN 机翼的计算域网格和局部壁面网格Fig.3 Computational mesh of LANN wing

对得到的非定常数据进行POD 模态分析，设置能量占比值为99.9%，得到的压力系数的降阶模态为r= 132.图4 给出了扫频信号激励下得到的非定常数据的平均值和前三个流场POD 模态的结构数据，可以看到每个模态都很好地反映了流场的激波位置，且随着模态的增加，其复杂程度也在增加.前三阶POD 分析中模态对应的时间系数，可以看到在扫频信号的作用下，POD 模态的系数整体趋势同样具有扫频特性，由于跨声速激波的原因，幅值变化会有很大的非线性特性，呈现出阶梯性跳跃的情况.

图4 流场数据的POD 模态分析Fig.4 POD mode analysis of unsteady fluid data on LANN wing

使用训练完的基于非线性系统辨识和模态分析方法构建的降阶模型，可以计算机翼在不同攻角下的定常流场，同时也可以计算机翼在不同运动形式下的非定常流场.对于前者，由于模型的构建是在时间序列信号的基础上所建立的，所以需要使用频率较大的斜坡函数来近似构造定常状态.对于给定的输入目标激励，计算其动态的非定常气动力需要考虑两个部分，一个为模态分析存储得到的POD 模态数据以及初始流场定常状态的流场数据，另一个为目标激励的非定常运动的POD 模态系数.在此基础上，以目标运动为系统的目标激励信号，使用降阶模型计算得到系统对应的POD 模态系数，最后把均值、模态和模态系数合在一起得到最终的目标非定常流场.

为验证降阶模型的适用性和准确性，使用构建的降阶模型计算机翼的非定常气动力.计算马赫数为Ma= 0.82 跨声速流场中做强迫俯仰运动，其俯仰运动为

式中：k=0.076；α0=0.6°；αm=0.25°.

俯仰运动轴位于65%根部弦长的位置.使用的目标激励信号的时间步长和训练信号一致，同为0.000 5 s，计算3 个周期共300 个时间步[19-20].在此基础上，使用150 个模态计算机翼在简谐运动下的非定常流场变化情况.图5 给出了升力系数和俯仰力矩系数随时间变化的曲线.可以看到，使用降阶模型得到的升力系数和力矩系数和CFD 直接得到的升力系数和力矩系数差距很小，误差都在5%以内，在攻角变化幅值为1 的时候升力系数的误差甚至都在2%附近.

图5 两种方法计算的升力系数和力矩系数的时间曲线Fig.5 Coefficients of lift force and moment with CFD and ROM

图6 给出了机翼在缩减频率为k=0.076,Ma=0.82流场条件下做俯仰运动其表面压力系数的一阶谐波的系数幅值的分布图，包括机翼上表面和下表面以及一阶谐波的实部和虚部两个部分.可以看到，机翼在简谐俯仰运动条件下的表面压力系数的一阶谐波的实部和虚部尽管存在着细节的差别，但是从整体趋势来说，使用降阶模型得到结果和CFD 直接得到的结果吻合得不错，都捕捉到了机翼在该马赫数下存在 λ型激波.这一结果表明构建的ROM 适合捕捉机翼流场的频率响应.

图6 非定常流场的一阶谐波幅值的机翼表面分布云图对比Fig.6 First-order harmonic amplitude of the unsteady flow field with CFD and ROM

为了更好地验证上述对于机翼表面压力系数的一阶谐波实部和虚部的幅值的变化对比的分析，图7给出了两个展向位置处实部、虚部幅值沿弦长的分布以及与实验数据的对比.可以看到，在靠近机翼翼根处的展向位置η= 0.200，两种方法计算得到的一阶谐波幅值和实验数据一样都在机翼上表面捕捉到了两道激波，下表面一道激波.对应上面对幅值在机翼表面的整体分布现象的分析，两种方法得到的结果在幅值大小和激波位置的捕捉上存在的差别.在展向位置为η= 0.475 处，数值计算方法得到的虚部幅值相对于实验数据，只在前缘和后缘处有着很好的吻合效果，在有着激波变化移动的弦长x/c=0.2 ～0.7的位置，依然有着巨大的差距.

图7 机翼展向位置为 η = 0.200, 0.475 处的压力系数的一阶谐波幅值对比Fig.7 First-order harmonic amplitudes of the pressure coefficient at η = 0.200, 0.475 spanwise position

综上所述，在经过降阶模型的辨识训练过后，使用本文构建的基于局部线性神经模糊模型的降阶模型在计算机翼作简谐俯仰运动的非定常流场有很好的计算精度.这些精度较高的结果大都体现在整体趋势，包括压力系数分布的结构形状、一阶谐波分析的实部或者虚部的幅值的变化趋势以及升力系数和力矩系数等，但在整个细节的捕捉方面存在着部分精度的缺失，主要是因为使用POD 模态分析方法进行降阶，使得原始数据的几千个模态降低到一百多个模态，但在工程应用的接受范围.

3.2 三维机翼跨声速颤振边界计算

本节使用经典的三维AGARD 445.6 气动弹性模型跨声速颤振边界的数值计算来说明本文建立的降阶模型在非线性气动弹性问题中的准确性和适应性，计算方法和结果都只考虑非定常气动力的非线性.AGARD 445.6 机翼颤振风洞实验是由美国国家航天局兰利研究中心（NASA Langley Research Center）在跨声速动态风洞（TDT）中完成的[21].为了检验跨声速机翼的颤振特性, 设计了一系列标准弹性机翼的风洞实验模型, 共有5 组不同的模型, 包括4 种硬模型和一种软模型.目前, AGARD 445.6 软模型已经成为国际上跨声速气动弹性程序考核的标准算例.风洞实验采用的AGARD 445.6 机翼模型的具体形状如图8 所示.

图8 AGARD 455.6 机翼的模型和流体计算网格Fig.8 Model and computational mesh of AGARD 455.6 wing

使用RANS 程序计算机翼的定常流动数值和在外部激励下的非定常流场数据，AGARD 445.6 机翼的计算模型的网格由混合网格组成，共有180 万个网格节点，280 万的网格单元.非线性辨识中常用的输入信号有白噪声或伪随机信号，因此本文在伪随机二进制序列（PRBS）信号的基础上，使用随机的幅值变化得到可变幅值的伪随机二进制序列信号（APRBS），用于降阶模型的系统辨识.该信号具有较宽的频率和幅值的密度分布，非常适合流场计算的非线性系统的辨识.

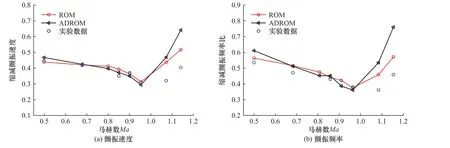
AGARD 机翼表面的非定常流场数据由URANS流体计算程序计算得到，流场条件设置：Ma= 0.500,0.678, 0.800, 0.850, 0.900, 0.954, 1.070, 1.140，计算的物理时间步长设置为4.5×10-4s，计算总的时间步为3 500步，湍流模型选择S-A 模型.采用结构的前三阶模态，因此输入信号为三通道的APRBS 信号，其频率范围足够广可以包含跨声速范围的颤振频率范围，即对于缩减频率k=ωcroot/U∞来说变化范围为0.133

3.2.1 固定马赫数下的颤振边界计算

对所有关注的马赫数情况下的AGARD 455.6 机翼的颤振边界进行分析，即首先根据使用非定常程序求得的非定常流场数据计算得到各个模态下的广义气动力系数，然后使用LOLIMOT 模型进行系统辨识计算各个缩减频率下的时域广义气动力，对其进行频域分析得到一阶谐波分析的实部和虚部构建广义力影响系数矩阵，最后使用p-k频域方法求解颤振边界.对AGARD 445.6 机翼在马赫数为Ma= 0.500,0.678, 0.800, 0.850, 0.900, 0.954, 1.072, 1.141 的条件下的临界颤振速度进行计算.图9 给出了其中两个马赫数Ma= 0.900 和Ma= 1.141 流场条件下计算得到的模态衰减率随速度的变化曲线.可以看到，在马赫数为Ma= 0.900 时，对于第一阶广义模态，其曲线首先开始时小于0，随着速度的增加穿过0 点变为正值，即AGARD 455.6 机翼在Ma= 0.900 条件下的颤振发生在第一阶模态，颤振速度为其衰减率变为0 的点，即VF= 291.7 m/s.对于马赫数为Ma= 1.141 时，颤振边界由第二阶模态决定，其衰减率变为0 的点为VF=466.6 m/s，因此使用量纲一的颤振边界表征参数量纲一的颤振速度分别为0.364 和0.517，对应的频率比分别0.423 和0.571.

图9 p - k 方法中不同模态的振动衰减因子随速度的变化曲线Fig.9 The attenuation factor of different modes varies with speed

图10 给出单马赫数降阶模型、自适应降阶模型以及实验数据计算得到的AGARD 455.6 机翼颤振边界和颤振频率比随马赫数变化的曲线.对比发现，在亚音速阶段，即马赫数为Ma= 0.499, 0.678 两个马赫数时，直接CFD 方法的计算结果和降阶模型计算结果都与实验结果吻合的很好；在剩下的马赫数为Ma=0.800～0.954 范围内，马赫数接近临界马赫数，机翼结构表面有着强力的激波作用，气动非线性作用非常剧烈，导致颤振边界的极速降低，往往是飞行器容易出现颤振问题的区域，从图中可以看到，直接使用CFD 方法计算得到的颤振速度的最大误差在8%，颤振频率比的最大误差为12.8%，而本文构建的降阶模型的颤振速度在该马赫数的误差只有2.24%，颤振频率比的误差为1.31%，这些表明降阶模型相较于直接CFD 计算方法不仅有着较高的计算效率还具有较高的计算精度，尤其在飞行器容易出现颤振问题的危险马赫数范围内.另一方面，马赫数Ma= 1.07, 1.14的超声速范围内，无论是降阶模型的计算结果还是直接CFD 的计算结果都和实验数据有着较大的误差，但本文的降阶模型也同样相较于直接CFD 计算方法有着较小的误差.可以看到本文构建的在单马赫数下的基于非线性系统辨识和模态分析方法的降阶模型可以很好地计算得到AGARD 455.6 机翼的颤振边界，并且在大大提高计算效率的条件下同时比直接的CFD 计算有着更高精度的计算结果，表明本文构建的ROM 的有效性和准确性.

图10 AGARD 455.6 机翼颤振边界随马赫数的变化曲线Fig.10 Flutter boundary with Mach number

3.2.2 变马赫数下的颤振边界计算

在基于参数化降阶模型的非定常气动力计算的基础上，结合频域内方法，可以使用本文发展的参数化的降阶模型构建在目标马赫数气动力未知的情况下计算该马赫数条件下的颤振边界.整个流程包括构建Grassmann 插值方法数据集、模态和对应的系数计算、广义力影响系数矩阵以及最后的颤振边界计算.插值计算的数据集为使用三通道的APRBS 信号在马赫数为Ma= 0.499, 0.678, 0.800, 0.850, 0.901,0.954, 1.070, 1.140 等8 个马赫数状态下计算得到的非定常数据，并对其进行数据分析得到POD 模态矩阵.使用能量准则得到满足99.9%能量占比的模态数目为r= 4.在这里，假设Ma= 0.901 状态下的流场数据未知，以其他剩下的7 个状态的数据为基点来说明使用本文构建的自适应降阶模型计算该马赫数的颤振边界的流程.

图11 给出单马赫数降阶模型、自适应降阶模型以及实验数据计算得到的AGARD 455.6 机翼颤振边界和颤振频率比随马赫数变化的曲线.对比发现，在亚声速阶段，即马赫数为Ma= 0.499, 0.678 两个马赫数时，单马赫数时的降阶模型计算结果与实验结果吻合的很好，自适应降阶模型的计算结果在马赫数Ma= 0.678 时也和单马赫数的计算结果有着很小的误差，且和实验结果吻合的很好，但在马赫数更小的Ma= 0.499 时，尽管处于亚声速状态，单马赫数降阶模型的计算结果和自适应降阶模型的计算结果的误差也显得比较大，尤其在频率比的数值上.原因在于在使用自适应降阶模型时，马赫数Ma= 0.499 时计算所有的数据为马赫数为Ma= 0.678～1.140 的7 个操作数据点，其超出插值的马赫数变化范围，导致数据计算精度降低.同样的现象也发生在马赫数为Ma= 1.140 时，颤振速度和ROM 的误差达到19.3%，频率比的误差为24.77%.在这个超音速速度下，不仅有着插值的误差，同时还有着激波误差的存在，导致误差非常大.除此以外，在剩下的跨声速速度范围内，ROM 和自适应降阶模型得到的计算结果基本相同，最大的误差即在超音速Ma= 1.070，颤振速度误差为6.62%，频率比误差为8.12%，都在可接受范围以内.无论是亚声速还是跨声速状态，自适应降阶模型方法和单马赫数的ROM 方法都精确捕捉了物面气动力的基本特征，其精度接近于CFD 直接模拟.计算结果体现了所建自适应降阶模型方法的正确性.同时注意到，尽管趋势相符，颤振计算和试验之间存在一定的偏差.因此，这些数据表明本文构建的单马赫数和马赫数自适应降阶模型均适用于跨声速颤振边界的计算，并且有着较好的准确度.

图11 AGARD455.6 机翼颤振边界速度和频率比随马赫数的变化曲线率Fig.11 Flutter boundary with Mach number

4 计算效率分析

对于跨声速颤振速度计算这种气动非线性的气动弹性问题，精确的数值模拟方法是适合时域内非线性气动弹性分析的CFD/CSD 耦合的分析方法，但由于其计算困难，一般使用基于模态的广义坐标和气动力的计算方程使用CFD 和结构运动方程耦合方式求解颤振速度.在这个方法中，一般需要改变非定常求解器的流场参数条件，重复计算去寻找颤振速度，即需要大量的调用流场求解器，一般需要循环10 个左右的动压才能比较准确找到颤振速度值，因此计算量非常巨大.因此，实际应用中即使使用CFD/CSD方法也会采用频域的p-k方法进行求解，只是在广义力系数影响矩阵的构建时采用的是基于非定常的Euler 或者N-S 方法进行计算，从而达到对气动非线性较为准确的捕捉.

以AGARD 455.6 机翼为例，在马赫数为Ma=0.901 条件下，AGARD 445.6 机翼的计算模型网格由混合网格组成，共有180 万个网格节点，280 万的网格单元，结构使用前三阶振型.在这些条件下，使用工作站电脑作为计算单位，其芯片为AMD Ryzen 9 3900X，计算时候开启全部的12 核并行.假设计算了8 个缩减频率下的简谐振动，每个运动计算了3 个周期，同时对于结构使用了前三阶振动模态，每个case的计算耗时为8 h 12 min，共有8×3 = 24 个case，所以加上定常收敛的计算耗时5 h 22 min 共耗时201 h.

另一方面，在单个马赫数下使用基于非线性系统辨识和模态分析方法的降阶模型计算AGARD445.6机翼在马赫数Ma= 0.901 条件下的颤振速度时的计算消耗为计算定常流场至收敛同样为5 h 22 min，计算3 500 个时间步的非定常流场数据花费时间为101 h 8 min，然后使用POD 模态分析、系统辨识、广义力系数影响矩阵的构建和最后的p-k方法的迭代计算，这些步骤的总共耗时约1 h 12 min，因此对于单个马赫数的颤振边界计算，使用基于LOLIMOT/POD 方法构建的降阶模型的计算消耗为108 h.

上面都是针对单个马赫数下的颤振计算情况所言，假设需要计算多个马赫数下的颤振边界，并需要画出比较精确的颤振边界随马赫数的变化曲线的情况下的计算效率如何？同样使用AGARD445.6 的算例为例，假设画出包含跨声速和部分超音速内的较为精确的颤振边界曲线，需要计算30 个马赫数情况下的颤振边界（跨声速和超音速范围内由于激波的存在对马赫数非常敏感，因此需要精细的马赫数划分），使用直接的循环动压迭代方法的计算耗时为305×30 = 9 150 h，使用CFD/CSD 构建广义力系数影响矩阵的方法的计算耗时为201×30 = 6 030 h，使用单个马赫数下的降阶模型的计算耗时为108×30 =3 240 h.使用本文构建的基于Grassmann 流形插值方法的高效非定常气动力计算方法并构建的参数化降阶模型的计算消耗为：

①使用单马赫数下的降阶模型计算8 个主要马赫数下的颤振边界耗时108×8 = 864 h；

②使用参数化降阶模型计算其他剩下22 个马赫数下的颤振边界耗时1 h 34 min×22 = 34.5 h；

③总的计算消耗为899 h.

5 结 论

本文建立了适用于多流场参数条件下非定常气动力高效计算的流场参数化降阶模型，解决了在非线性气动弹性分析时需要在时域求解多个流场参数条件下结构运动方程而造成的计算消耗过大的问题.在参数化降阶模型的构建中，基于POD 模态分析理论，为了高效地计算目标流场参数条件下的POD 模态形状，研究了基于Grassmann 流形的模态插值方法，发展了一种对数映射算法修正的测地线方法，不仅在POD 模态插值计算过程中有着较高的计算精度，而且适用于流场参数变化过大的情况.另一方面，针对模态系数，构建了基于局部线性神经模糊模型的非线性系统辨识方法的流场参数变化条件下的模态系数的计算.最终结合模态计算方法、系数计算方法以及POD 模态分析理论，建立了适用于多个流场条件下非定常流场数据计算的参数化降阶模型，在LANN 机翼的计算算例中得到了很好的计算结果，并成功应用于典型机翼的跨声速颤振边界的计算，大大提高了计算效率.