基于多载波阵的定域调制技术
徐友根,张译文
(北京理工大学 集成电路与电子学院,北京 100081)
近年来,作为无线物理层安全领域的重要技术之一,定向调制引起了人们的极大关注.定向调制技术能够将待发送的信号发射到预先设定的通信方向上,而在其他方向上的接收信号星座图被扰乱,接收机无法正确解调信号,从而实现加密通信.
定向调制技术的实现主要有两类,一类是在射频前端实现定向调制[1-4],通过天线开关、移项器、可重构天线元件等硬件来改变阵列的辐射场,从而在远场得到不同的星座图,实现信号的定向调制,该类方法受制于硬件条件,系统实现较复杂.另一类实现定向调制的方法是在基带端生成定向调制信号[5-8],发射的基带信号由固定分量和时变的干扰分量两部分组成,固定分量用来承载信息,时变分量与固定分量正交,其作为噪声对非期望方向上的信号进行干扰,并以符号速率对时变项进行更新.误码率是评价定向调制系统性能的准则之一,YUAN[9]给出了基于定向调制的误码率的修正形式.
以上定向调制技术仅能实现角度维的安全通信,当通信接收方与窃听方位于同一角度但是不同的距离时,上述方法将会失效.频控阵的概念于2006 年提出[10],通过对每个阵元上的发射载频施加一个微小的频偏,使得远场辐射方向图同时依赖于角度和距离,葛佳昂等[11]对频控阵与相控阵的相位方向图特性进行分析比较.线性频偏方案将会导致频控阵波束方向图出现距离-角度耦合现象,王博等[12]则分析了不同非线性频偏方案的距离-角度解耦性能.频控阵的出现为定向调制技术实现提供了一种新的可能,XIONG 等[13]首次将频控阵与定向调制技术相结合,利用遗传算法对每个阵元的相移值进行优化求解,实现了距离-角度定位调制.文献[14 - 15]分别提出基于随机频偏和对称频偏的频控阵定位调制方案.CHENG 等[16]提出基于时变频偏的定位调制方法.WANG 等[17]以非零安全容量概率作为衡量标准来计算窃听方与发射方之间需达到的最小距离,以保证发射方与通信方之间信息的安全传输.ZHANG 等[18]提出了基于多载波的定位调制阵列结构,其基带实现方法类似于传统的OFDM 系统,并针对工作在不同载频下的不同调制符号分别求加权矢量.
与利用遗传算法求解定向调制信号加权矢量不同[2,13],WU 等[19]从目标函数出发,通过设计期望辐射场的幅度函数和相位函数,并利用伍德沃德-劳森方法来综合得到理想的目标函数,所提方法可以产生更窄的信息波束宽度,提高系统的安全性,与基于遗传算法的定向调制技术相比,所提方法从解析法的角度入手,具有闭式解,算法复杂度较低.然而,该方法也仅能实现角度维的安全通信,对于与通信方向处于同一角度但是不同距离的窃听方来说不具备安全通信的能力,且较窄的信息波束宽度虽具有很高的安全性,但当发射机所指定的位置与实际的接收位置存在失配时,接收机的信号接收性能将会明显下降.因此,本文在上述定位调制技术的基础上,将伍德沃德-劳森方法扩展至距离-角度维,提出一种对位置误差不甚敏感的定域调制技术,其信息传输误码率的零陷宽度可在一定范围内进行调整,从而可在通信安全性和鲁棒性之间进行适当的折衷.仿真结果表明,所提定域调制方法可保证在整个预先设定的角度区域和距离区域内都具有较好的信号接收性能.
1 多载波阵系统模型
考虑一个具有M个发射阵元的均匀线性多载波阵,阵元间距为d,如图1 所示.每个阵元上的子载波均为[f0+Δf1,f0+Δf2,···,f0+ΔfK],K为单个阵元上的子载波数目,f0为中心频率,Δfk为第k个子载波与中心频率之间的频率间隔,可表示为

图1 多载波阵阵列结构Fig.1 Multi-carrier array structure
其中, Δf为基础频率间隔,且Δf≪f0.
在远场空间中某一点(r,θ)处的发射波束方向图可以表示为
式中:c表示光速;zm表示各阵元的位置坐标;wm,k表示加权矩阵W的第m行第k列元素,有
由于频率间隔Δfk远小于中心频率f0,式(2)中的最右端的Δfkzmsinθ因f0zmsinθ的存在可以被忽略.则多载波阵发射波束方向图可进一步表示为
式中:w表示矩阵W按列排成一列; ⊗表示Kronecker 积;aθ和ar分别表示角度维和距离维导向矢量,有
由式(4)可以看出,多载波阵的发射波束方向图是时变的,可采用谢滔等[20]所提出的定向调制接收机结构在接收端进行波形分离,从而使得接收信号是距离-角度相关的且时不变的,因此本文在下面的讨论中不再考虑时间变量.
2 定域调制信号综合算法
2.1 角度-距离维伍德沃德-劳森法
伍德沃德-劳森(Woodward-Lawson)采样综合法通过在一些离散的位置对方向图进行采样以逼近期望方向图.传统的伍德沃德-劳森方法通过对一维的理想目标函数进行采样,以得到期望的角度维波束方向图,当不考虑能量衰减时,其仅能实现角度维的能量聚集,当窃听方与通信方处于同一角度但是不同的距离时,窃听方接收到的信号能量与通信方相当,很容易造成信息的泄露.本节将一维伍德沃德-劳森法扩展至角度-距离维,将能量聚焦在设定的区域内.从公式(4)看出,多载波阵的导向矢量由角度维导向矢量和距离维导向矢量两部分组成,当仅考虑公式(5)所示的角度维导向矢量时,阵列相当于传统的相控阵,可以利用一维伍德沃德-劳森方法求得期望角度维波束方向图所对应的角度维导向矢量wθ.当仅考虑公式(6)所示的距离维导向矢量时,将角度维方向图综合的思路扩展至距离维,即可得到距离维期望方向图所对应的距离维权矢量wr,下面详细介绍距离维权矢量的求解过程.
当不考虑时间变量t时,此时的距离维导向矢量为
其中,v=2πΔf(r0-r)/c.
由式(8)可知,方向图在r=r0处取得最大值,方向图的零点位置满足
则有
其中,rNPk表示激励为时的波束方向图的第k个零点的位置.
其中,ri0表示激励所形成波束方向图的主瓣指向,且r00=r0,bi表示各个激励的幅度值.
此时各个激励电流的主瓣指向为
以式(12)所示的各个位置作为期望方向图的抽样点,抽样间隔为c/(KΔf),以期望方向图对应距离上的值来确定各个激励的幅度值bi,即可产生能逼近期望方向图的阵列激励.
综上所述,角度-距离维伍德沃德-劳森法实现步骤如下:
1) 确定距离维的能量聚焦区域;
2) 根据式(12)得到距离维的采样点;
3) 根据期望方向图对应距离上的值来确定各个激励的幅度值bi;
4) 根据式(11)得到距离维的阵列激励wr;
5) 确定角度维的能量聚焦区域;
6) 结合式(5),重复步骤2)~4),得到角度维的阵列激励wθ;
7) 多载波阵的总的阵列激励为W=.
图2 给出了基于多载波阵的一维伍德沃德-劳森法得到的角度维平顶波束方向图和角度-距离维伍德沃德-劳森法得到的二维平顶波束方向图.根据所设定的角度维波束宽度和距离维波束宽度,角度维和距离维的主瓣范围分别为-5°≤θ≤ 5°和0.95 km≤r≤1.05 km.由图2(a)的方向图能够看出,传统的一维伍德沃德-劳森法仅仅能够将能量聚焦在所设定的角度范围之内.图2(b)中,角度-距离维伍德沃德-劳森法成功实现了在设定的角度区域和距离区域内的平顶波束,将能量聚焦于所设置的区域之内.值得注意的是,伍德沃德-劳森法得到的方向图在设定区域内会产生波纹起伏,从而影响区域内的信号能量,但是该现象对本文所提定域调制技术不会产生较大影响,下文将结合实验结果进行分析.
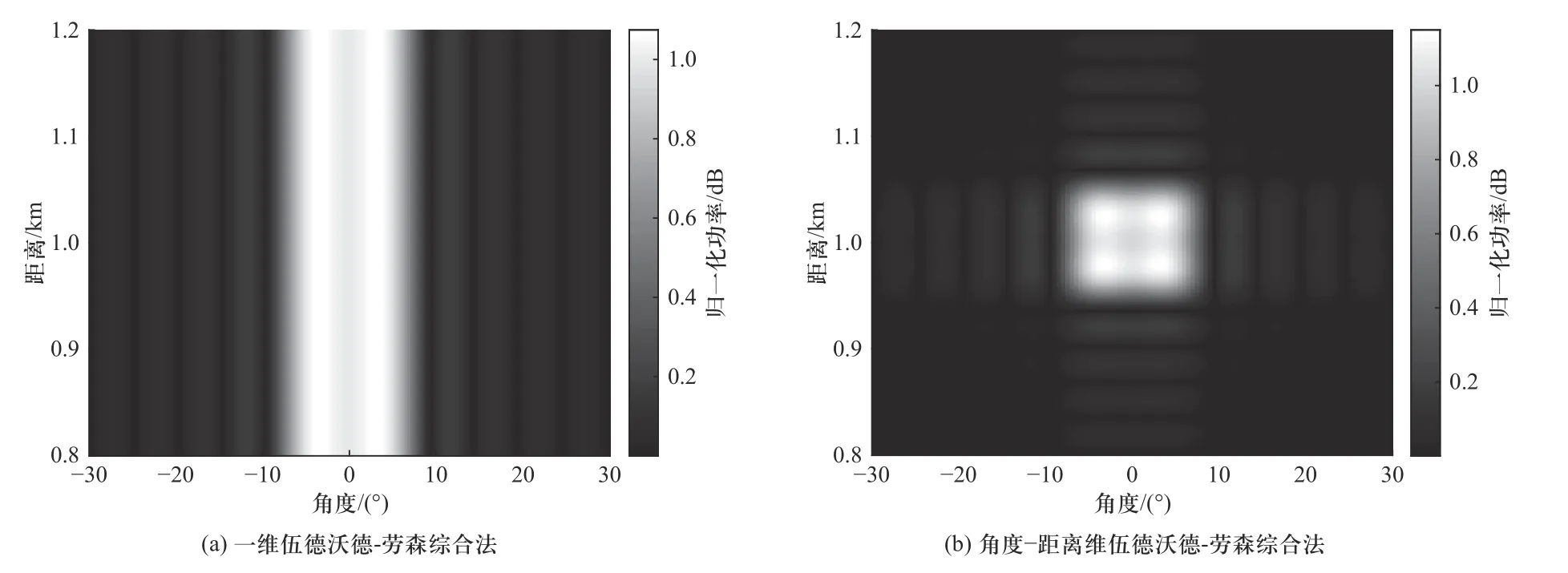
图2 波束方向图对比Fig.2 Beampattern comparison
2.2 定域调制技术实现
在基带端生成定位调制信号的方法中,发射机端传输的基带信号由两部分组成,一部分是有用信号,另一部分是随机矢量.基于上述角度-距离维伍德沃德-劳森方法,在所选采样角度和距离所对应的多载波阵流形矢量所张成空间的正交补空间中随机选择一个矢量,即可对非信号能量汇聚区域的信号进行加密.
期望接收区域内所选角度和距离对应的多载波阵流形矢量组成的流形矢量矩阵可表示为
其中,L表示区域内采样点的数目.当(rd1,θd1)≠(rd2,θd2)时,a(rd1,θd1)与a(rd2,θd2)线性无关,因此当L≤MK时,流形矢量矩阵A为列满秩矩阵.则向A的列空间的正交补空间进行投影的正交投影矩阵为
对于任意向量b,可通过正交投影矩阵将其投影在A的列空间的正交补空间内,即
利用式(15)可以得到一个与 的列空间正交的一个向量,也即
于是定义投影矩阵PAN为
利用式(17)可将任意一个随机矢量投影到A的列空间的正交补空间内,以保证该随机矢量的存在不会干扰预先设定区域内的信号接收,而在设定区域之外,信号的幅度和相位均会因为随机矢量的存在而产生扰动,这种扰动也会随着位置变化而随机改变,从而达到对非信号能量汇聚区域的信息进行加密的目的.
此时基带所发射的信号为
其中,xq表示待发送的有用信号,且满足=1,以QPSK 信号为例,有xq∈{ejπ/4,ej3π/4,e-j3π/4,e-jπ/4}.Ps为发射信号的平均功率, α为有用信号和随机矢量之间的功率分配因子,w为角度-距离维伍德沃德劳森法求得的波束成形矢量,AHw中的元素均为实数且近似为1,z∈CMK×1为随机矢量.
假设所有的信道都是视距通信信道,此时,在所设置区域内的通信方接收到的信号为
其中,nd为通信方接收机接收到的复高斯白噪声,其分布满足CN(0,σ2).
所设置区域外的窃听方所接收到的信号为
其中,nu为窃听方接收机接收到的复高斯白噪声,其分布满足CN(0,σ2).
可以看出,随机矢量的存在对区域内的通信接收方不会产生影响,而在设定区域之外的窃听方位置上,式(20)中前两项的存在使得接收信号的幅度和相位均存在不同程度的扰动,星座点将被扰乱,从而使得接收机无法正确解调所接收到的信号.
3 数值仿真性能及其分析
基于上述所提的基于多载波阵的定域调制技术进行仿真来验证所提方法的安全通信性能.本文采用一个24 阵元的均匀线阵,阵元间距为c/2f0,每个阵元上的载波数目K设置为30,中心频率f0为10 GHz,基础频率间隔 Δf为300 kHz,所设置区域的中心角度和距离为(θ0,r0)=(0°,1 km),角度维的波束宽度设置为10°,距离维的波束宽度设置为100 m,阵列观测区域为{(θ,r)|-30°≤θ ≤30°,0.8 km ≤r≤1.2 km}.采用接收端的幅度方向图、相位方向图、误码率图、以及不同位置处的接收信号星座图来评价系统的安全性能,误码率按照文献[9]的式(6)进行计算.
图3 和图4 分别给出了不同角度和不同距离处接收信号的幅度和相位变化图.在角度维,图3(a)和图3(b)给出了在期望位置(r0=1 km)处的接收信号幅度和相位随角度变化的图,可以看出,在所设定的角度区域内,接收信号幅度较强,且4 个信号之间的相位差基本保持恒定;在所设定的角度区域之外,接收信号幅度较弱,降低信号被截获的概率,且接收信号的相位杂乱无章,即使信号被高灵敏度的接收机接收到,由于4 个信号之间的相位关系被扰乱而无法被正确解调.图3(c)和图3(d)给出了在位置(r=1.08 km)处的信号幅度和相位随角度变化的图,可以看出,4 个信号的幅度和相位均是杂乱无章的,接收机无法正确解调信号.在距离维,图4(a)和图4(b),图4(c)和图4(d)分别给出了在期望角度(θ0=0°)处,以及角度(θ=12°)的接收信号幅度和相位随着距离变化的图,在设定的角度区域和距离区域之内,接收信号幅度较强,且4 个信号之间的相位关系保持不变,信号很容易被接收机接收到且能够被正确解调;而在设定的角度区域之外,在任何距离上信号的幅度较小,且信号之间的相位关系被扰乱,对接收机的接收和解调造成困难.

图3 角度维QPSK 信号幅度和相位图Fig.3 QPSK signal amplitude and phase pattern with angle

图4 距离维QPSK 信号幅度和相位图Fig.4 QPSK signal amplitude and phase pattern with range
图5 给出了在一些位置处的接收信号星座图,图6 则给出了所提定域调制系统的误码率,并与传统的定位调制的误码率进行对比.图5(a)~(e)为所设置的角度-距离区域内几个特定位置处的星座图.图5(a)中,(0°,1 km)处接收到的4 个信号分别为0.95∠45°(0.95 表示信号的幅度,45°表示信号的相位,以下同理)、0.95∠135° 、0.95∠-135° 、0.95∠-45°,图5(d)中,(2°,1 km)处接收到的4 个信号分别为0.99∠44°、1.00∠135° 、0.99∠-137° 、1.05∠-45°,可以看出,4 个信号之间的相位差基本保持在90°附近,幅度基本保持一致.图5(f)为设置区域之外的一个位置处的星座图,此时的接收信号为0.04∠-69° 、0.07∠105°、0.04∠-144° 、0.05∠-155°,很明显,此时的接收信号幅度较小,且信号之间的相位关系被扰乱,即星座图被扰乱.由图6 可以看出,所提方法将误码率图进行了展宽,在所设定的区域之内,误码率保持一个较低的水平,而在所设定的区域之外,误码率较高,在保障安全性的同时,通过对误码率零陷的展宽使得系统对于位置误差比较鲁棒.

图5 不同位置处的星座图Fig.5 Constellations at different locations

图6 误码率图Fig.6 BER pattern
图7 给出了角度维和距离维的误码率曲线.与传统定位调制的误码率相比,定域调制的误码率得到了一定程度的展宽.虽然在设定的区域内,误码率曲线有一定的起伏,这是因为伍德沃德-劳森方法综合得到的波束方向图在设定的区域内会产生波纹,从而对误码率产生影响,但是区域内的误码率总体保持在一个较低的水平,而在所设定的区域之外,定域调制的误码率与定位调制的误码率水平大致相当,保持在一个较高的水平.
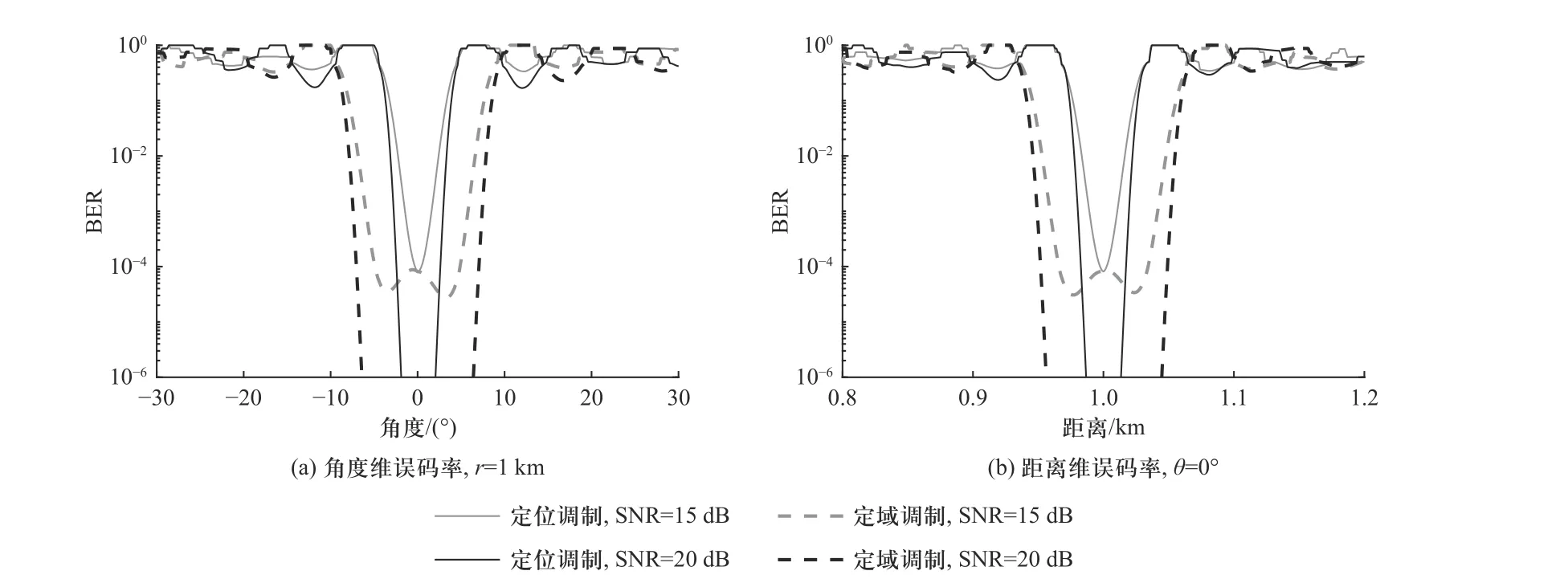
图7 不同信噪比下的误码率曲线Fig.7 BER curve under different SNR
图8 展示了误码率随阵元数目进行变化的情况.当阵元数目较少时,角度维误码率曲线零陷宽度较宽,几乎在所有角度上的误码率水平都比较低,此时系统的安全性能较差.随着阵元数目的增加,误码率曲线零陷宽度变窄,继续增大阵元数目,误码率曲线又慢慢得到展宽,并在设定的区域内保持一个较低的误码率水平,并且从距离维误码率曲线可以看出,阵元数目的变化对距离维的误码率曲线的影响不大.图9 展示了误码率随载波数目进行变化的情况,载波数目的变化对角度维误码率曲线影响不大.当载波数目为1 时,所提的多载波阵相当于传统的相控阵,没有距离维的加密功能,此时的距离维误码率曲线为一条直线.随着载波数目的增加,距离维误码率曲线零陷宽度逐渐变窄,继续增大载波数目,误码率曲线逐渐得到展宽,且在设定的距离区域内保持较低的误码率水平.因此,要想实现误码率零陷宽度在设定的小范围角度区域和距离区域内的展宽,阵元数目和载波数目不能太少.
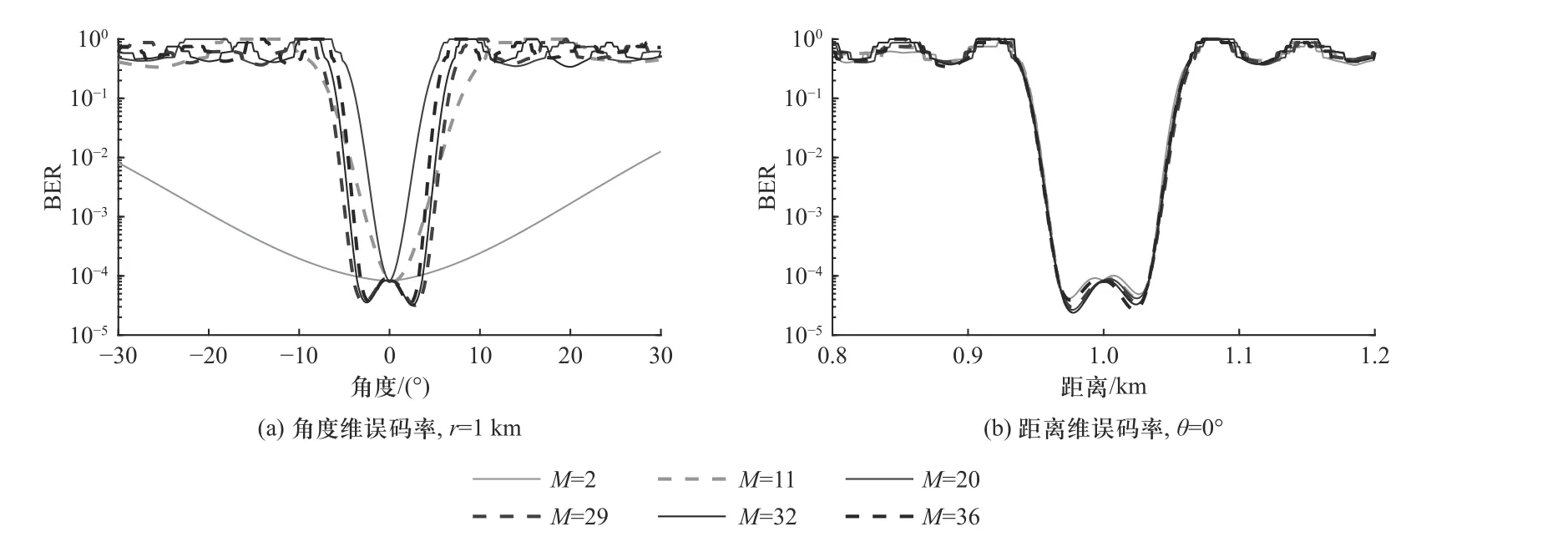
图8 误码率随阵元数目的变化曲线Fig.8 BER curve with the number of antennas
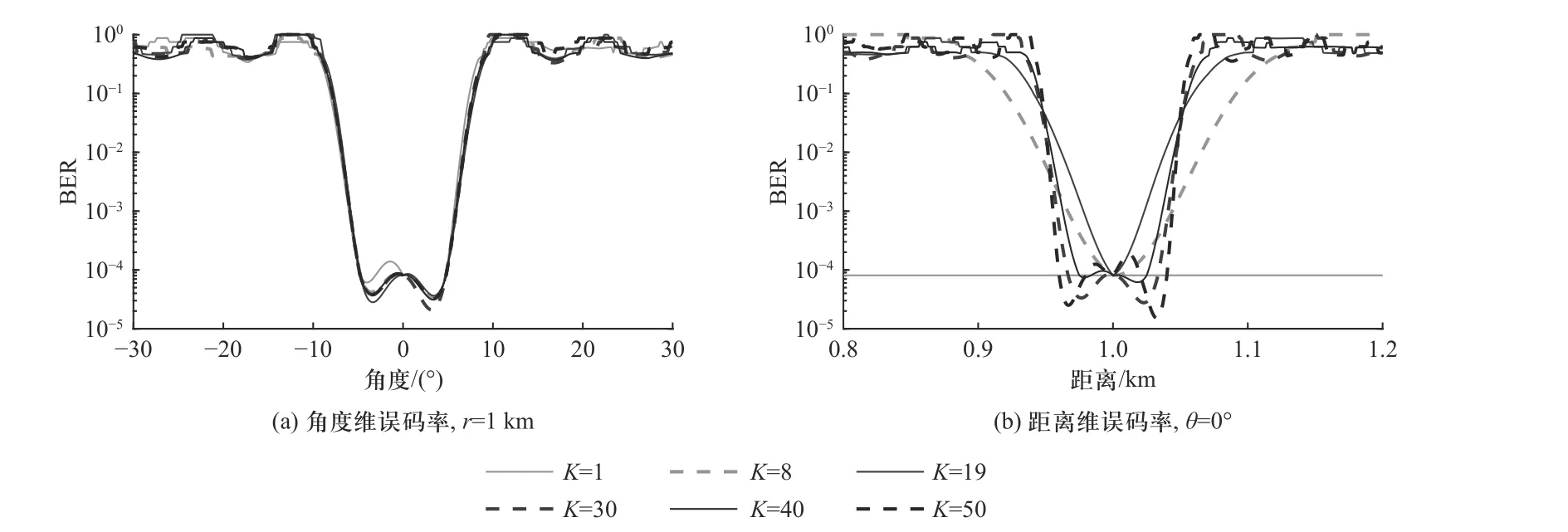
图9 误码率随载波数目的变化曲线Fig.9 BER curve with the number of carriers
4 结 论
本文提出了一种基于多载波阵的定域调制技术,可将发射信号能量聚焦在一个预先设定的可调区域内,使得该区域内具有较高的信噪比,同时通过叠加随机正交矢量的方式实现了非信号能量聚焦区域的加密.与传统的定位调制相比,定域调制将误码率图进行了展宽,保证了接收方在预先设定的区域内接收信号星座图不失真,区域内误码率较低,而不在该区域内的接收信号的幅度和相位则存在不同程度的扰动和星座图失真,误码率较高,所提方法对于存在位置误差的情况具有一定的鲁棒性.此外,为了在设定区域内实现较低的误码率水平,本文所提阵列结构对阵元数目和载波数目具有一定的要求,当阵元数和载波数越大时,误码率在设定区域的展宽程度越好.

