善析条件结论,实现一题多解——以一道几何证明题为例

⦿ 西华师范大学 胡澳丽

1 问题呈现

图1

求证:BC2+CD2=2BD2.

2 试题分析

该题是初中的一道综合性几何证明题,考查的知识点较多,重在培养学生对知识的掌握以及运用能力,实现对知识的巧妙运用,达到举一反三的效果.从题目所给条件及结论入手,可从四个不同的角度对题目进行分析证明.

3 特色解法

视角一：根据条件AB=AD,利用等腰三角形构造旋转,形成“手拉手”模型.

证法1：如图2,将△ADC绕点A按顺时针方向旋转到△ABE,连接CE.

图2

∴△ADC≌△ABE.

∴△ADB∽△ACE.

又∠ABE=∠ADC,∠BAD+∠BCD=90°,

∴∠EBC=90°.

在Rt△EBC中,由勾股定理,得

BC2+BE2=EC2.

∴BC2+CD2=2BD2.

证法2：如图3所示,将△ABC绕点A按逆时针方向旋转到△ADE,连接CE(按证法1步骤同理可得结论,解答过程略).

图3

视角二：根据条件∠BAD+∠BCD=90°,利用互余条件巧构直角,寻找特征线段间的数量关系.

证法3：如图4,过点C作线段BC的垂线,截取CE=CD,连接BE,DE.

图4

∵BC⊥EC,
∠BAD+∠BCD=90°,
AD=AB,DC=EC,

∴△DAB∽△DCE.

∴△ADC∽△BDE.

在Rt△BCE中,由勾股定理,得BC2+EC2=BE2.

∴BC2+CD2=2BD2.

证法4：如图5,过点A作线段AB的垂线,取点E,使得∠EDA=∠BDC.

图5

∵EA⊥AB,
∠BAD+∠BCD=90°,

∴∠DAE=∠DCB.

又∠EDA=∠BDC,

∴∠AED=∠CBD.

∴△BCD∽△EAD.

∴△EDB∽△ADC.

∵AD=AB,

∴AE=kBC,AB=kCD,DE=kBD.

在Rt△AEB中,有AE2+AB2=BE2.

代入化简,得BC2+CD2=2BD2.

证法5：如图6,分别延长AB,AD至点E和点F,使DF=AD,BE=AB,连接CF,CE,EF,则BD是△AEF的中位线,EF=2BD.

图6

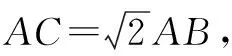
∴△ABC∽△ACE.

∵∠1+∠2+∠3+∠4=90°,

∴∠1+∠2+∠5+∠6=90°.

∴∠FCE=90°.

由勾股定理,得CE2+CF2=EF2.

∴BC2+CD2=2BD2.

证法6：如图7,取AC的中点E,连接ED,EB.

图7

又∠BAC=∠EAB,

∴△BAC∽△EAB.

∵∠BAD+∠DCB=90°,

∴∠EBA+∠EDA+∠BAD=90°.

由三角形内角和为180°,得∠BED=90°.

由勾股定理,可得BE2+ED2=BD2.

∴BC2+CD2=2BD2.

证法7：如图8,过点B作BE⊥BC,使得BE=CD,连接AE,CE.

图8

在四边形ABCD中,

∠ADC=270°-∠ABC.

∵∠ABE=270°-∠ABC,

∴∠ADC=∠ABE.

∴△ADC≌△ABE(SAS).

∴∠DAC=∠BAE.

∴∠DAB=∠CAE.

又AD=AB,AC=AE,

∴△ABD∽△AEC.

在Rt△CBE中,由勾股定理,可得

BC2+BE2=CE2.

∴BC2+CD2=2BD2.

4 结语

对于证明题的作答,学生首先要认真审题,挖掘题目所涉及的知识点以及它们之间的内在联系,体会其中的数学思想,把握命题者的出题意图,从而高效解题.

善于分析题目,巧挖掘条件,从题目中抓重点,尝试从不同角度解题,实现一题多解.一题多解不仅能扩宽学生解题思路、提高学生解决问题的能力,而且能让学生体会其中的数学思想,发展数学学科的核心素养.Z