借助“一题多解”,倡导“一题多变”——一道向量试题的探究

⦿ 江苏省泰兴市第二高级中学 李 明

作为高中数学中的一个重要知识点与基本解题工具,平面向量凭借自身同时兼备“数”的基本属性与“形”的结构特征这一内涵,成为高中数学中一道特殊的亮丽风景线.

在实际数学试题的命制与解题过程中,往往可以从“数”与“形”这两个不同的视角加以切入与应用,丰富问题的内涵与实质,也为问题的解决提供更加多样变化的视角,体现创新性与应用性.

1 问题呈现

问题已知平面向量a,b,c满足|a|=1,b·c=0,a·b=1,a·c=-1,则|b+c|的最小值为( ).

本题通过三个平面向量之间的关系加以合理创设,结合其中一个向量的模以及这三个向量之间的数量积,合理构建这三个平面向量之间的关系,得以确定其中两个向量线性关系的模的最值问题.主要考查平面向量的模、数量积等基础知识,运算求解等能力,数形结合、化归与转化等思想,体现基础性、综合性与创新性等,导向对直观想象、逻辑推理、数学运算等核心素养的关注.

波利亚曾说:“掌握数学就是意味着善于解题.”抓住平面向量的内涵与实质,结合具体问题,从平面向量的“数”与“形”这两个不同的视角来切入,通过代数运算或几何直观等方面来合理数学运算、逻辑推理等.

2 问题破解

2.1 几何思维

方法1：几何意义法.

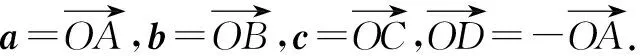
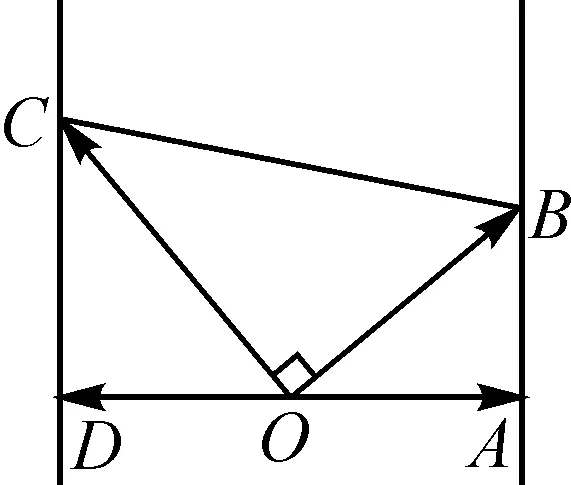
图1

解后反思：根据平面向量“形”的几何特征,结合平面向量的几何内涵或几何意义,从“形”的视角切入,通过数形结合加以直观想象,从几何特征层面来研究对应的问题.这里结合平面向量数量积的几何意义,从射影、垂直等视角来直观处理,利用图形直观,结合“动”态变化规律来解决“静”态的最值问题.

2.2 代数思维

方法2：坐标法1.

解析：在平面直角坐标系xOy中,设向量a=(1,0),b=(x1,y1),c=(x2,y2),如图2所示.因为a·b=1,a·c=-1,b·c=0,所以x1=1,x2=-1,x1x2+y1y2=0,则y1y2=1.

图2

方法3：坐标法2.

因为a·b=1,a·c=-1,所以mcosα=1,-nsinα=-1,即mcosα=1,nsinα=1.

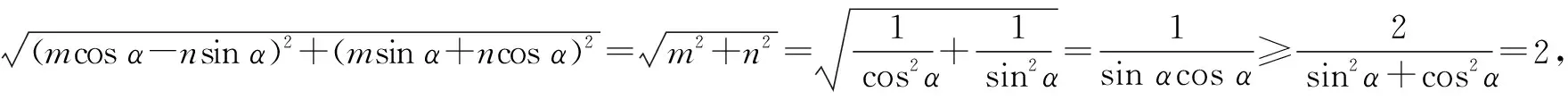
解后反思：根据平面向量的“数”的基本属性,通过平面直角坐标系的构建,合理引入平面向量的坐标,利用平面向量中的相关要素,转化为涉及坐标的函数、方程或不等式等,进而从代数视角进行数学运算与逻辑推理.这里通过平面向量所对应的坐标的构建,利用题设条件确定对应坐标的关系式,结合基本不等式的放缩、三角函数的应用等来确定与应用.

2.3 三角函数思维

方法4：基本不等式法.

方法5：三角函数法.

解后反思：根据平面向量的“数”与“形”的融合与应用,引入向量的模或夹角等相关几何量,将向量问题转化为与向量的夹角等相关的三角函数问题,在解决一些相关的最值问题或取值范围问题时经常用到.这里从不同向量的夹角设置或从整体性思维设置向量的夹角等不同方式加以创设,转化为对应的三角关系式,通过三角恒等变换与应用,结合基本不等式或三角函数等来放缩处理.

3 变式拓展

契合以上数学问题的思维视角的“一题多解”,深挖问题的内涵与本质,合理归纳总结,创新应用提升,合理拓展变式与应用,全面实现数学基础知识、数学思想方法与数学能力等方面的提升.

3.1 低阶变式

降低题目难度,简化推理过程与数学运算.

3.2 同阶变式

保持题目条件,变换求解视角.

变式3已知平面向量a,b,c满足|a|=1,b·c=0,a·b=1,a·c=-1,则|b+c|的最小值为( ).(C)

3.3 高阶变式

提升题目难度,深化推理过程与数学运算.

变式4已知平面向量a,b,c满足|a|=1,a·b=b·c=1,a·c=2,则|a+b+c|的最小值为______.(4)

4 教学启示

4.1 “数”“形”结合,开拓思维

平面向量集“数”“形”于一体,是“数”与“形”巧妙融合的和谐统一体,更是沟通代数与几何的一种有效解题工具.在实际应用过程中,可以从平面向量“数”的视角切入,合理渗透函数与方程、三角函数、不等式等“数”的代数性质;也可以从平面向量“形”的视角切入,合理融入平面几何、平面解析几何等“形”的几何内涵.从“数”与“形”这两个层面展开,真正实现技巧策略的应用与核心素养的养成这二者之间的和谐与统一.

4.2 发散思维,“一题多得”

借助“一题多解”进行数学思维的锻炼与提升,可以促进学生更加系统、全面地理解并掌握对应的数学知识与解题方法,并在此基础上不断提升数学问题的综合性、灵活性与创新性,巧妙深入探索,实现“一题多变”“一题多用”“一题多得”的良好效果,拓宽并加强数学思维和数学能力等,举一反三,触类旁通.