揭示2023年上海卷第21题本质

⦿ 山东省胶州市第三中学 胡晓洁

1 题目:2023年上海卷第21题

已知f(x)=lnx,取点(a1,f(a1))过其作曲线y=f(x)的切线交y轴于点(0,a2),取点(a2,f(a2))过其作曲线y=f(x)的切线交y轴于点(0,a3),若an≤0则停止,以此类推,得到数列{an}.

(1)若正整数m≥2,证明:am=lnam-1-1;

(2)若正整数m≥2,试比较am与am-1-2的大小;

(3)若正整数k≥3,是否存在k使得a1,a2,……,ak依次成等差数列?若存在,求出k的所有取值;若不存在,试说明理由.

2 分析与思维导图

2.1 思维分析

本题从导数与数列的综合运用出发,考查学生求切线方程、构造函数证明不等式、等差数列性质的应用以及方程有解问题的解决能力,体现了数学抽象、逻辑推理、数学运算等核心素养.本题的题干是由函数图象的切线与y轴相交,交点的纵坐标经过递推得到一个数列.递推的过程和利用牛顿法求方程的解类似.数列在题目中更多是起到背景和提示作用,本质上还是解决函数与导数的问题.本题作为上海卷的压轴题,有较大的思维量,突出考查了数学抽象和逻辑推理核心素养.

第(1)问证明数列的递推关系,本质上考查求函数的切线方程,要求学生理解题目中的递推关系.本题对学生在给定情境下分析数学问题的能力有较高的要求.

第(2)问比较大小,常用办法是将要比较的对象化成同一变量后作差.结合第(1)问的结论,可以发现本质上是考查常用不等式lnx≤x-1(ex≥x+1)的证明.本题要求学生能够结合已知结论解决问题,熟练掌握构造法证明不等式.

第(3)问分析k的取值是难点,结合等差数列的性质,可以将分析k的取值转化为方程有解的问题.不同的性质可以转化出不同的方程,此问主要利用公差和等差中项来解决.本题要求学生能深刻地理解方程有解和函数有零点的等价关系.

2.2 思维导图

第(3)问的思维导图如图1所示.

图1

2.3 解答

(Ⅰ)第(1)问的解答:

(Ⅱ)第(2)问的解答:

解：当m≥2时,am=lnam-1-1,am-1>0.

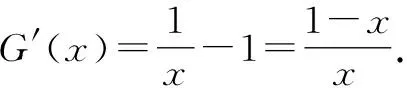
所以,当00,G(x)在(0,1)上单调递增;当x>1时,G′(x)<0,G(x)在(1,+∞)上单调递减.

所以,G(x)≤g(1)=0,即am-(am-1-2)≤0.

故am≤am-1-2.

(Ⅲ)第(3)问的解答:

解法1：列举式解题.

假设存在k符合题意,即a1,a2,……,ak依次成等差数列,设公差为d.

当k≥4时,因为am≤am-1-2,所以d=am-am-1≤-2.

所以{ak}既是等差数列也是等比数列,即{ak}为常数列,显然与am≤am-1-2矛盾.

当k=3时,a1,a2,a3为等差数列,设公差为d,所以d=a3-a2=a2-a1≤-2.

所以lna2-a2-1=lna1-a1-1=d.记g(x)=lnx-x-1,则g(a2)=g(a1)=d.

显然,当d=-2时,因为-2=a2-a1=lna1-a1-1,所以a1=1,a2=-1,则不存在a3,所以d<-2.

下面只需证明:函数h(x)=g(x)-d=lnx-x-1-d对任意d<-2都存在两个零点.

易知:g(x)在(0,1)上单调递增,在(1,+∞)上单调递减.

所以h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,则且h(x)≤h(1)=-2-d.

所以h(1)=-2-d>0,h(ed)=-1-ed<0.

所以φ(t)<φ(4)=ln 4-3<0,则h(-2d)<0.

所以,h(x)=g(x)-d=lnx-x-1-d对任意d<-2都存在两个零点x1,x2,且x1∈(0,1),x2∈(1,+∞).故k=3.

解法2：渐进分析式解题.

假设存在k符合题意,即a1,a2,……,ak依次成等差数列,设公差为d.

当k=3时,a1,a2,a3为等差数列,设公差为d,所以d=a3-a2=a2-a1≤-2.

所以lna2-a2-1=lna1-a1-1=d,即g(a2)=g(a1)=d.

显然,当d=-2时,因为-2=a2-a1=lna1-a1-1,可知a1=1,a2=-1,则不存在a3,所以d<-2.

易知,g(x)在(0,1)上单调递增,在(1,+∞)上单调递减.

所以h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,则h(x)≤h(1)=-2-d.

所以h(1)=-2-d>0,h(ed)=-1-ed<0.

所以φ(t)<φ(4)=ln 4-3<0,则h(-2d)<0.

所以,h(x)=g(x)-d=lnx-x-1-d对任意d<-2都存在两个零点a1,a2,且a2∈(0,1),a1∈(1,+∞).

因此a3<0,停止递推.所以k的取值只能为3.

解法3：整体分析式解题.

假设存在k符合题意,即a1,a2,……,ak依次成等差数列,设公差为d.

显然,当d=-2时,因为-2=a2-a1=lna1-a1-1,可知a1=1,a2=-1,则不存在a3,所以d<-2.

因为d=ak-ak-1=lnak-1-ak-1-1,则a1,a2,……,ak-1为方程lnx-x-1-d=0解.

所以函数h(x)=g(x)-d=lnx-x-1-d有k-1个零点.

下同法1.

解法4：消元,构造函数零点.

假设存在k符合题意,即a1,a2,……,ak依次成等差数列,所以ak+ak-2=2ak-1.

因为ak=lnak-1-1,ak-1=lnak-2-1,所以eak-1+1+lnak-1-1=2ak-1.

因此ak-1为方程ex+1+lnx-1=2x的解,也即函数F(x)=ex+1+lnx-1-2x的零点.

所以a2=t时,a1,a2,a3依次成等差数列;但a3<0,递推停止.故k=3.

3 溯源与高考链接

2023年上海卷第21题是导数与数列的综合问题,命题背景来自人教A版教材选择性必修第82页的“牛顿法”.由函数的切线通过递推得到数列,要求解的是数列问题.但通过分析题意,寻找解题的切入点会发现本题三问实际考查的都是导数问题.下面两道高考试题供大家欣赏:

分析：由题意写出切线方程,找到ak和ak+1的关系.

(2015年江苏卷第20题)设a1,a2,a3,a4是各项为正数且公差为d(d≠0)的等差数列.

(1)证明:2a1,2a2,2a3,2a4依次成等比数列;

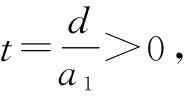
4 练习

①当a=0时,求曲线y=f(x)在点(1,f(1))处的“曲率”;

②若函数f(x)存在零点,求a的取值范围;

③设等比数列{an}的公比为q,

(扫码看练习参考答案.)