保持架兜孔形状对高速角接触球轴承保持架动态性能的影响分析

陈世金, 邹冬良, 王亚坤, 蔡东明

(五冶集团上海有限公司,上海 201900)

高速角接触球轴承广泛应用于航空发动机主轴、航天惯性仪表、新能源汽车主轴以及高速精密机床主轴等高速转子系统中,轴承性能以及寿命往往决定着系统能否正常运行,而保持架的动态特性是保证高速球轴承性能的关键。保持架不稳定运动不仅会使轴承力矩波动,产生啸叫声,还会加剧保持架磨损,甚至使其断裂,从而引起轴承精度丧失或使轴承卡死造成灾难性后果[1]。Kingsbury[2]第一次通过试验发现了保持架不稳定运动与轴承力矩波动之间的关系,认为轴承钢球与保持架兜孔之间的摩擦力驱动保持架涡动,保持架的不稳定涡动导致轴承摩擦力矩波动并产生啸叫声。Walters[3]最早建立了球4自由度、保持架6自由度的球轴承动力学模型,奠定了滚动轴承保持架动力学分析的基础。Gupta[4-8]建立了所有零件具有6自由度的滚动轴承完全动力学模型,可以模拟时变工况下轴承零件的瞬态运动特性,并系统分析了工况、润滑、摩擦以及几何等因素对保持架稳定性的影响。国内基于滚动轴承动力学模型的保持架动态特性研究近10年有了较快发展,Liu等[9-14]以Gupta动力学模型为基础针对各自工况进行一定简化,对保持架的动态性能分析提供了诸多有益探讨。分析指出,保持架兜孔间隙和引导间隙等是影响保持架动力学性能的重要参数,然而上述学者大多针对的是单一的圆柱形兜孔保持架,保持架兜孔形状作为对保持架结构影响更大的参数反而未被深入探究。此外,由于动力学模型较复杂,国内学者大多采用集成较多内部函数的Matlab语言进行程序开发,以降低程序开发难度,但是由于Matlab语言计算效率较低,程序运行耗时非常长,给出的结果中保持架甚至未进入稳定运行阶段(仿真轴承运行时间不到0.1 s)。Sathyan等[15]通过试验探究发现方形兜孔保持架摩擦力矩的稳定性数倍优于圆柱形兜孔保持架。邓四二等[16]利用能量守恒定律,建立角接触球轴承摩擦力矩理论计算公式,发现低速时方形兜孔保持架有利于轴承摩擦力矩的降低,反之则是圆柱形更有利。Yan等[17]建立了球6自由度、内圈5自由度和保持架3自由度的球轴承拟动力学模型,分析了球兜孔和圆柱兜孔对轴承温度的影响,结果表明球形兜孔保持架更利于轴承的散热。

综上所述,众多学者对保持架动力学特性探究做了诸多探索,但主要集中在工况、润滑、摩擦、兜孔间隙和引导间隙等方面,对保持架结构影响非常大的兜孔形状则较少涉及。而工程人员发现在某轴承中采用圆柱兜孔保持架时会产生啸叫声,而改换成方形兜孔保持架后啸叫声会减弱甚至消失。Sathyan等和邓四二等的研究表明兜孔形状对轴承摩擦力矩以及散热有较大影响,但由于未建立完全动力学模型,缺乏对保持架的动力学特性分析,且仅对某两种兜孔形状进行探讨,缺乏对不同保持架兜孔形状的综合讨论。陈世金等[18]试验探究了不同兜孔形状对轴承保持架质心轨迹和打滑率的影响规律,发现兜孔形状对保持架运动影响显著,但对其内在作用机理缺乏足够分析。本文在上述试验研究工作的基础上,以高速角接触球轴承为研究对象,分别建立方柱形(方形)兜孔、圆柱形(圆形)兜孔以及球形兜孔保持架的球轴承动力学数值仿真模型,并采用Fortran语言进行程序开发,大幅提高计算效率,分析轴承运行2 s内不同兜孔形状以及间隙比对保持架运动、受力以及磨损的影响,探究兜孔形状对保持架运动的作用机理,并以试验分别对三种兜孔保持架的动力学模型加以验证。

1 模型建立

本文基于课题组建立的高速仪表转子轴承动力学磨损数值仿真模型,建立了方形、圆柱形和球形保持架动力学模型,球和不同兜孔形状保持架的相互作用及保持架与引导套圈的相互作用介绍如下,球和内外圈的相互作用可以参考Zhang等。

1.1 坐标系与变换

假定轴承各零件几何中心与质心重合,轴承各坐标系中心建立在零件几何中心上,各零件的质心运动在惯性坐标系中描述,绕质心的转动在其定体坐标系。轴承各零件坐标系的定义如图1所示。

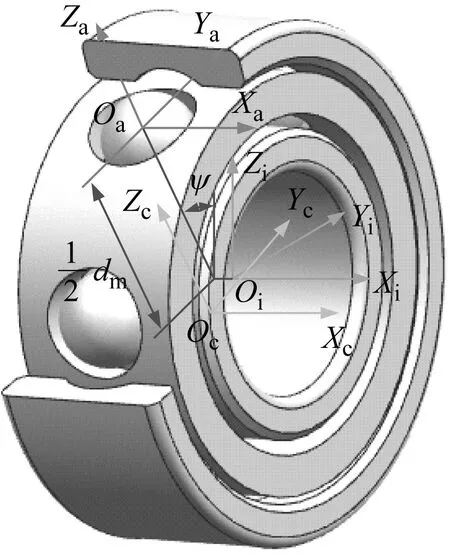
图1 轴承各零件坐标系定义Fig.1 Definition of coordinate system

从一个坐标系到另一个坐标系的转换可以通过三次相继的旋转实现,转换矩阵是

(1)

零件在定体坐标系中的角速度与三次旋转的角度(η,ξ,λ)之间的关系为[19]

(2)

式中,(ω1,ω2,ω3)为轴承零件在定体坐标系中的角速度分量。

1.2 保持架的运动方程

保持架在空间中共有6个自由度,分别为保持架的质心运动以及保持架的旋转运动,保持架在三维空间的质心运动可以在惯性坐标系中描述

(3)

式中:mc为保持架的质量;xc,yc和zc为保持架在惯性坐标系中的位置;Fcx,Fcy和Fcz分别为保持架所受的总力在x,y和z方向的分量。

保持架的旋转运动(动量矩方程)可以在其定体坐标系中描述

(4)

式中:mc为保持架的质量;Ic1,Ic2,Ic3为保持架转动惯量;ωc1,ωc2,ωc3为保持架的角速度在不同方向的分量;Mc1,Mc2,Mc3为作用于保持架的合力矩在不同方向的分量。

根据拟静力学结果给定保持架的初始位置和速度,采用变步长的四阶Runge-Kutta法对上述微分方程求解,即可得到保持架在任意时刻的位置、速度、载荷以及磨损率等。下面将介绍保持架与球以及引导套圈的相互作用,以得到保持架的所受的合力和合力矩。

1.3 保持架球与的相互作用

图2(a)～(c)分别为方形兜孔、圆形兜孔和球形兜孔保持架的结构示意图。由于保持架与球形兜孔保持架的计算最为复杂,本文以球与球形兜孔保持架的相互作用为例进行介绍。

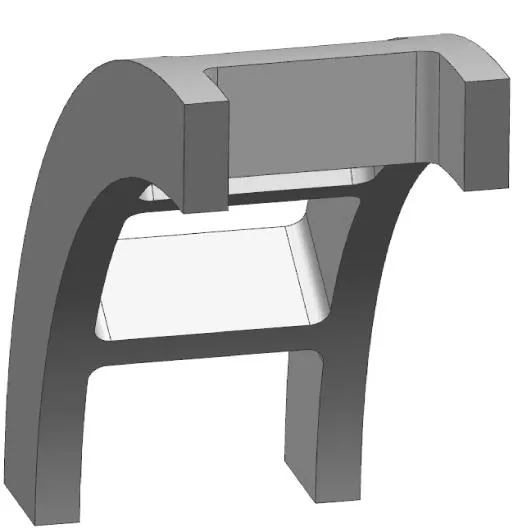
(a) 方形兜孔

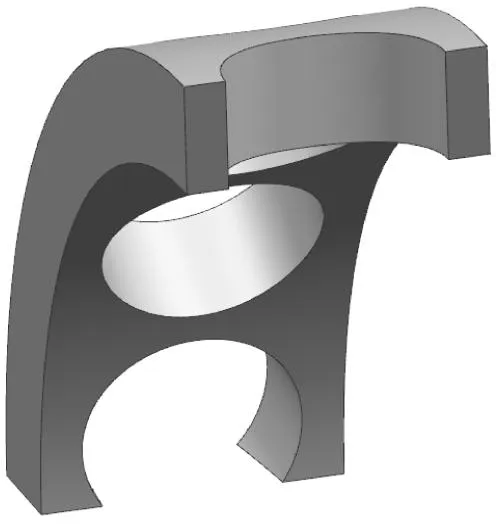
(b) 圆形兜孔

(c) 球形兜孔图2 不同形状兜孔保持架结构图Fig.2 Structural diagram of pocket cages with different shapes

如图3所示,惯性坐标系中,球心相对保持架中心的位置向量为

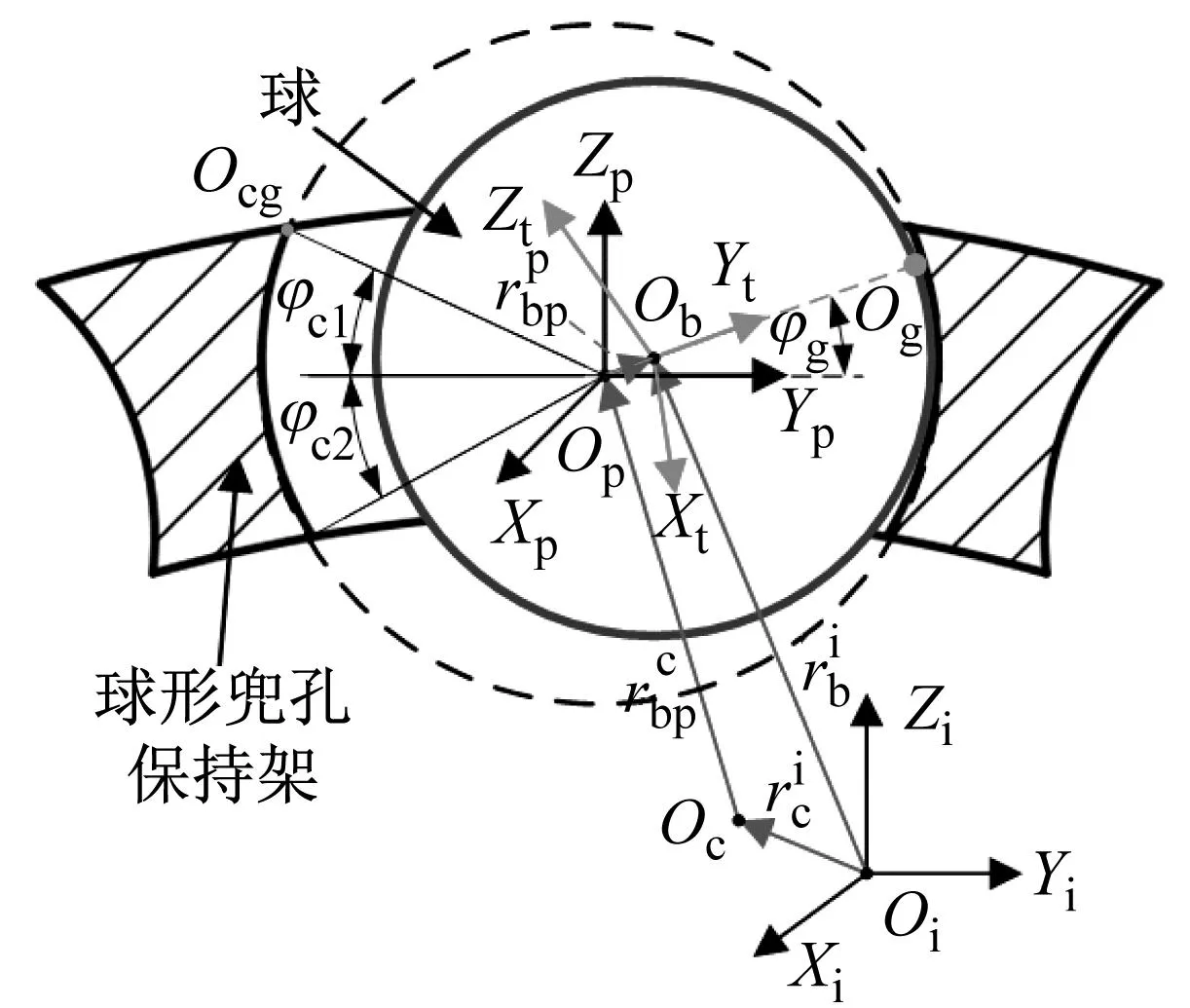
(a) 碰撞点在兜孔球面

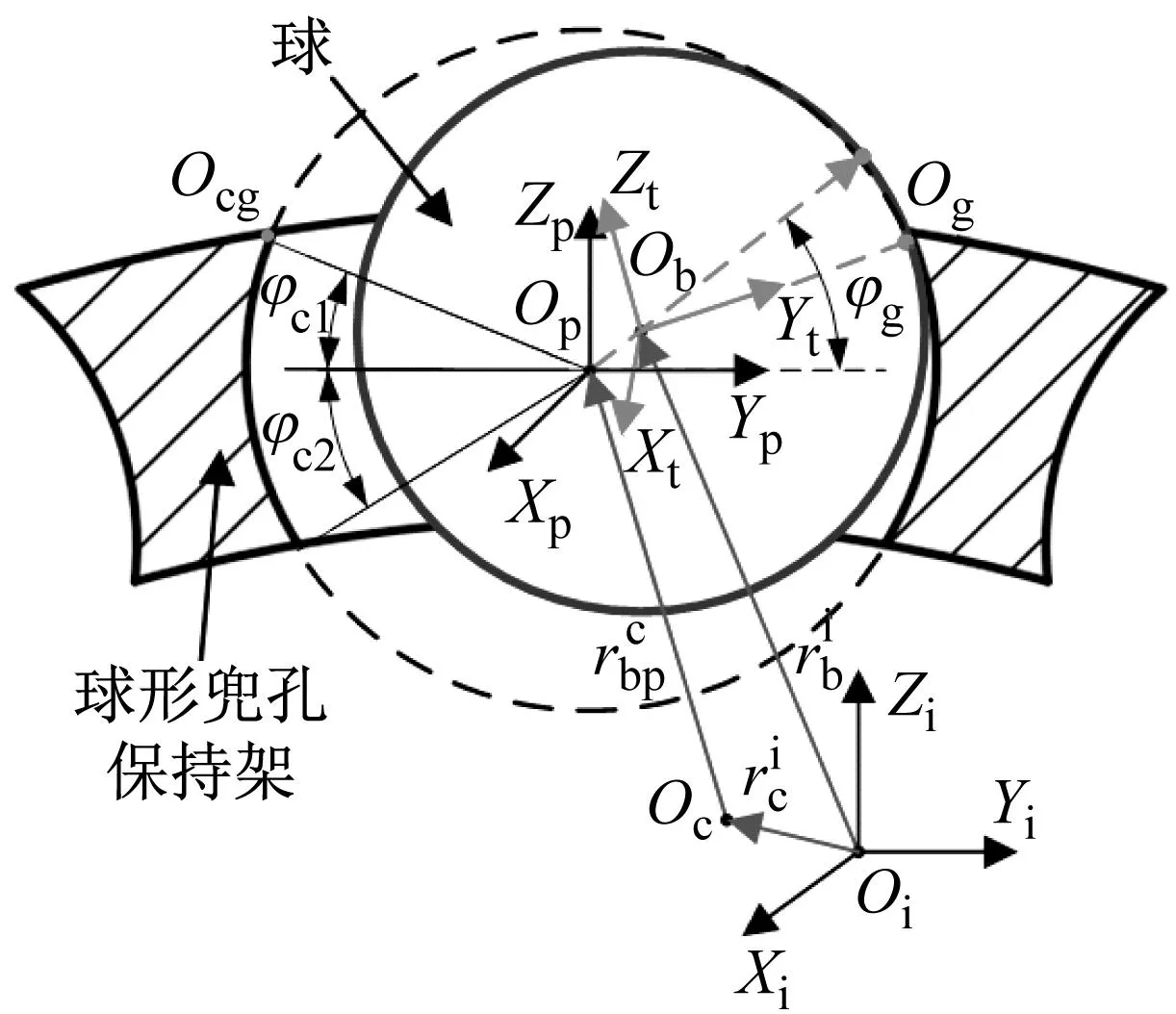
(b) 碰撞点在兜孔边界图3 球与球兜孔保持架的相互作用Fig.3 Interaction between ball and spherical pocket cage

(5)

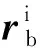
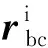
(6)

式中,Tic=T(φc1,φc2,φc3)为从惯性坐标系到保持架坐标系的转换矩阵,φc1,φc2和φc3为保持架的姿态角。

保持架坐标系中,第j个兜孔中心到保持架中心的位置向量为

(7)

式中,θp=2π(j-1)/z为第j个兜孔在保持架坐标系中的方位角。

保持架兜孔坐标系中,球心相对兜孔中心的位置向量为

(8)

式中,Tcp=T(θp,0,0)为保持架坐标系到兜孔坐标系的转换矩阵。

如图3所示,当φc2<φg<φc1时,球与保持架兜孔的碰撞点Og在兜孔球面内,当φg≤φc2或φg≥φc1时,碰撞点Og在兜孔球面与保持架内圈或外圈圆柱面的相贯线上,兜孔球面与保持架内圈和外圈的相贯线方程为

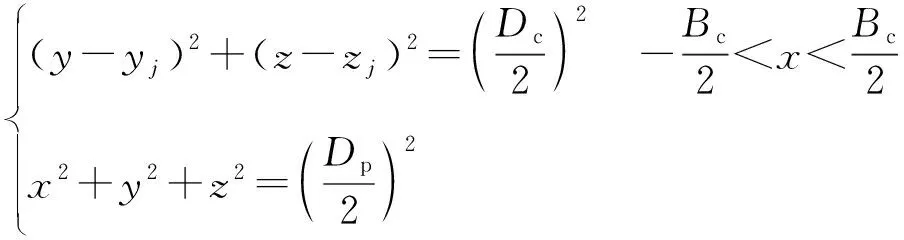
(9)

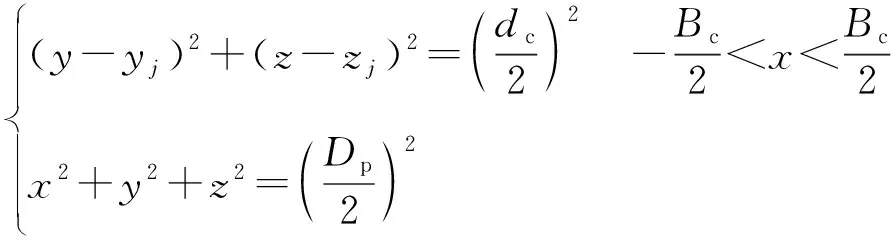
(10)

式中:yj,zj为保持架质心在j个兜孔坐标系中的坐标值;Dc,dc,Bc分别为保持架的外径、内径和宽度。

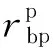
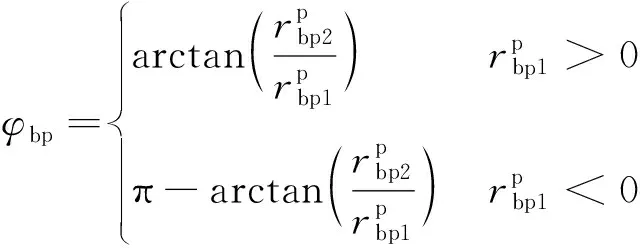
(11)

因此,边界点Ocg的坐标值满足

(12)

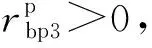
(13)

(14)

(15)

当φc2<φg<φc1时,球与兜孔的碰撞点在兜孔坐标系中的位置角为

(16)

(17)

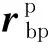
(18)

式中,Tpg=T(φ1,0,φ3)为从兜孔坐标系到接触坐标系的转换矩阵。

球与兜孔的接触变形量为

(19)

当φg≤φc2或φg≥φc1时,碰撞点Og相对球心Ob在兜孔坐标系中的位置向量为

(20)

因此球与兜孔的碰撞点在兜孔坐标系中的位置角为

(21)

(22)

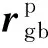
(23)

此时,球与兜孔的接触变形量为

(24)

球与兜孔之间的法向力可计算得

(25)

式中,Kbc为球与保持架兜孔的载荷-变形系数。

则球与兜孔之间的切向力为

Ftc=μcQc

(26)

式中,μc为球与兜孔之间的摩擦因数,设为恒定值。

保持架坐标系中,接触点相对保持架中心的位置向量为

(27)

式中,Tcg=TpgTcp为保持架坐标系到接触坐标系的转换矩阵。

球与兜孔接触坐标系中,球和保持架在接触点处的线速度分别为

(28)

(29)

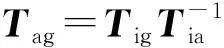
接触点处保持架相对球的滑动速度矢量为

(30)

则滑动速度的大小为

(31)

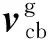
对于保持架与球及引导套圈的相互作用,由于滑动速度较大且接触区较小,可以作为点或线接触来计算瞬时磨损率,且一般认为磨损主要发生在保持架上。保持架单个兜孔的瞬时磨损率可计算得

(32)

式中:Kc为保持架的磨损系数;Hc为保持架材料的布氏硬度。

沿接触椭圆长轴和短轴的切向分力根据滑动速度的方向确定

Ftcx=Ftcsinφcb

Ftcz=Ftccosφcb

(33)

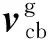
接触坐标系中,球受到保持架的作用力矢量为

(34)

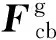
(35)

惯性坐标系中,保持架受到单个球的作用力矢量为

(36)

为便于分析保持架受力对于保持架质心运动的影响,定义了如图4中所示的保持架方位坐标系。方位坐标系的原点Oca固定于保持架几何中心,Xca轴沿轴承轴向,Zca轴径向向外。将保持架受到的作用力在方位坐标系中分解,得到各力在保持架质心轴向、径向和圆周运动方向上的分力。因此,在保持架方位坐标系中,保持架受到单个球的作用力矢量为

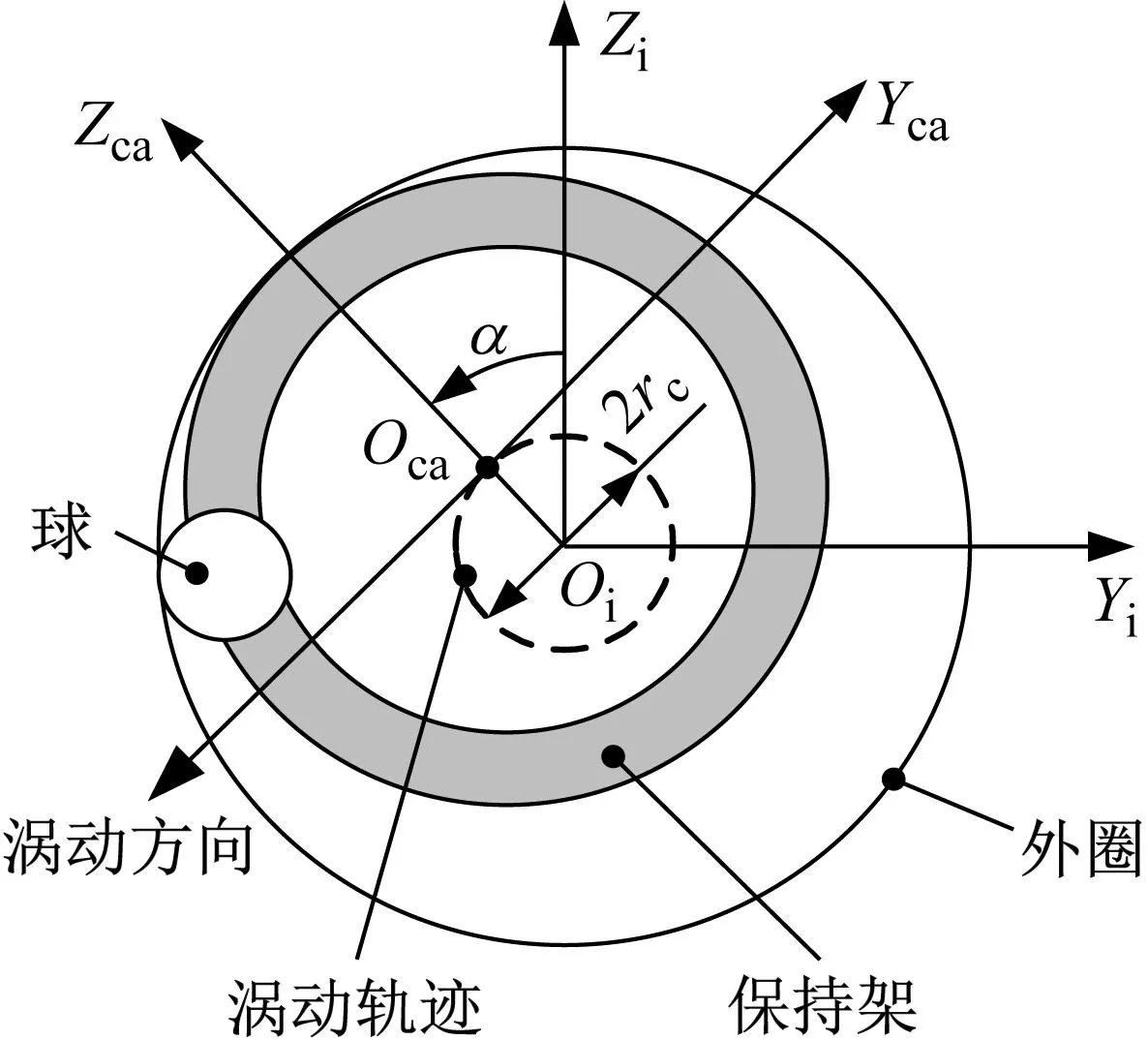
图4 保持架方位坐标系OcaXcaYcaZcaFig.4 The cage azimuth coordinate system OcaXcaYcaZca

(37)

式中,Tica=T(α,0,0)为惯性坐标系到保持架方位坐标系的转换矩阵。

球的方位坐标系中,球受到保持架的力矩矢量为

(38)

保持架坐标系中,保持架受到单个球的力矩矢量为

(39)

此外,对于方兜孔和圆兜孔保持架可采用类似的方法建模,主要区别在于方兜孔和圆兜孔沿径向是直的,球与保持架之间碰撞力在径向分量为零,无需判断碰撞点的径向位置,且仅需绕Zp轴旋转一次即可将保持架兜孔坐标系转换到接触坐标系,因此建模相对更容易,本文不再赘述。

1.4 保持架球与引导套圈的相互作用

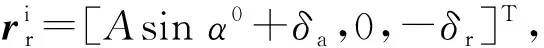
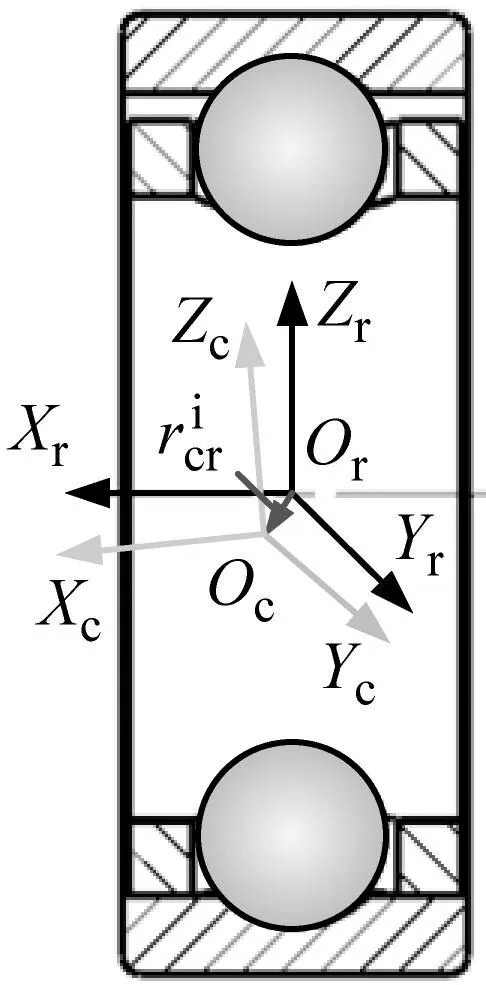
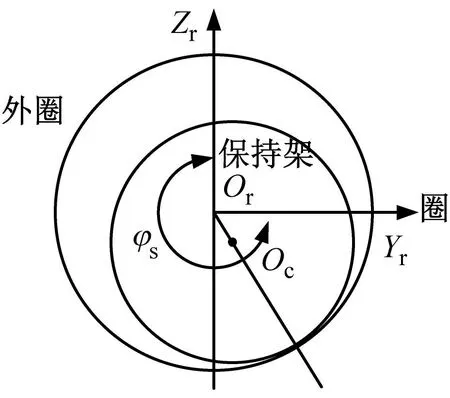
图5 保持架与引导挡边的相互作用Fig.5 Interaction between cage and guide land

惯性坐标系中,保持架中心相对外圈中心的位置向量为

(40)

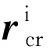
(41)

保持架与外圈的接触点在外圈坐标系中的方位角为

(42)

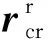
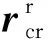
(43)

式中,Trs=T(φs,0,0)为外圈坐标系到接触坐标系的转换矩阵。

保持架与引导套圈的接触变形量为

(44)

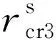
保持架与引导套圈之间的法向力由Hertz线接触公式计算得

(45)

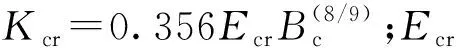
由此可得保持架与引导套圈之间的切向力

Ftr=μrQr

(46)

式中,μr为保持架与引导套圈之间的摩擦因数,设为恒定值。

外圈坐标系中,接触点相对外圈中心的位置向量为

(47)

保持架坐标系中,接触点相对保持架中心的位置向量为

(48)

接触坐标系中,保持架和套圈引导面上接触点处的线速度分别为

(49)

(50)

接触坐标系中,引导面上套圈相对保持架的滑动速度为

(51)

则滑动速度的大小为

(52)

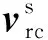
保持架与引导套圈的接触中,保持架引导面上的瞬时磨损率为

(53)

接触坐标系中,沿引导面轴向和周向的切向分力分别为

Ftrx=-Ftrsinφrc

Ftry=Ftrcosφrc

(54)

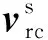
接触坐标系中,保持架受到引导套圈的作用力矢量为

(55)

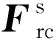
(56)

式中,Tis=TrsTir为从惯性坐标系到保持架与套圈接触坐标系的转换矩阵。

保持架坐标系中,保持架受到引导套圈的力矩矢量为

(57)

1.5 保持架所受的合力及合力矩

惯性坐标系中保持架受到的合力为

(58)

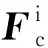
保持架坐标系中保持架受到的合力矩为

(59)

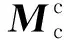
由此,即可得到保持架所受的合力以及合力矩,采用Runge-Kutta法对式(3)和式(4)进行求解即可得到保持架任意时刻的位置和速度。

2 仿真结果分析

利用上述模型,以某高速角接触球轴承为例,分析不同兜孔形状以及兜孔间隙对保持架质心运动、受力以及磨损率的影响。保持架所受的作用力均在保持架方位坐标系中分析,保持架方位坐标系的建立见图4。轴承结构和材料参数如表1所示。

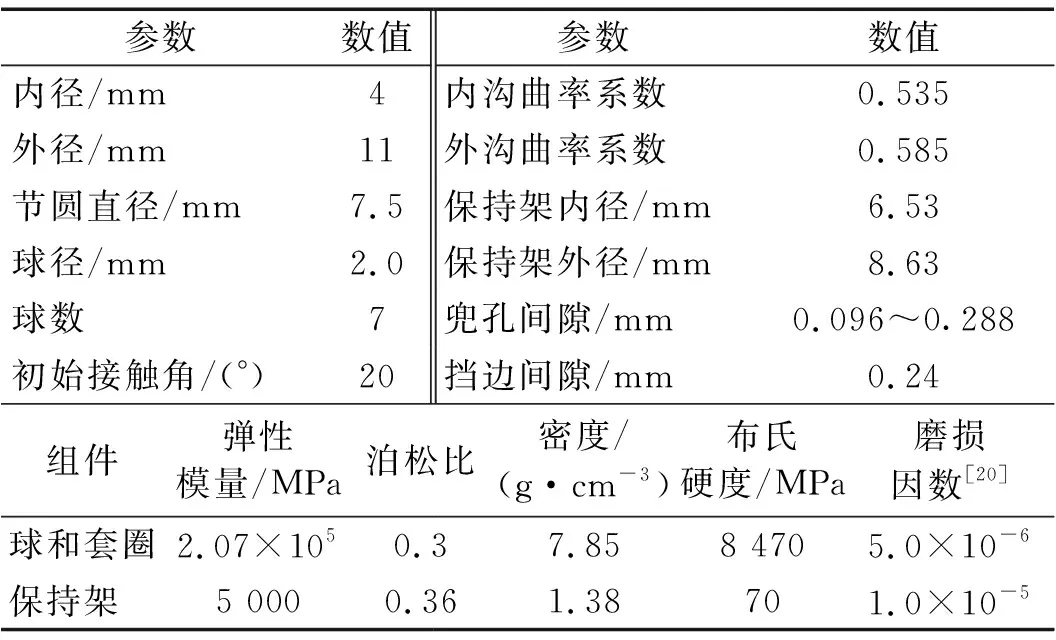
表1 轴承几何和材料参数Tab.1 Bearing geometry and material parameters

兜孔间隙Cb分别取0.096 mm,0.135 mm,0.240 mm和0.288 mm,对应的间隙比(兜孔间隙Cb与引导间隙Cr的比值)分别为0.40,0.56,1.00和1.20。该轴承所处的工况为,轴向预载荷7 N,内圈转速30 000 r/min。需要说明的是,由于本文计算程序采用Fortran语言编写,大幅提高了计算效率,本文所有结果都选取仿真轴承运转达到稳定后的值(取仿真1～2 s的结果,舍弃前1 s的结果)进行分析。

2.1 保持架运动稳定性分析

图6分别给出了不同兜孔形状的保持架在不同兜孔间隙下的三维质心运动轨迹,需要说明的是图中空间曲线表示保持架的三维质心运动轨迹,左侧曲线和下侧点分别是三维运动轨迹在YZ平面(径向平面)以及XY面的投影,分别表示保持架在径向平面的涡动以及轴向摆动。可以看出,随着兜孔间隙的增大,方形和圆形兜孔保持架的三维质心运动轨迹逐渐由圆柱形变为不规则形状,而球形兜孔保持架的三维质心运动轨迹则始终处于较规则的圆柱形。从XY平面的投影可以看出,随着兜孔间隙的增大,方形和圆形兜孔保持架的涡动轨迹逐渐由圆形变为多边形,说明保持架的运动越来越不稳定,而球形兜孔保持架则始终处于稳定的涡动状态。此外,在不同兜孔间隙下,方形和圆形保持架的涡动轨迹直径始终等于套圈引导间隙;而球形兜孔保持架则随着兜孔间隙的增大而逐渐增大,且保持架质心轨迹直径等于或略小于兜孔间隙,当兜孔间隙大于引导间隙时,球形兜孔保持架的涡动轨迹直径才等于引导间隙。这说明,不同间隙比下,方形和圆形保持架始终是由套圈引导的,而球形兜孔保持架则由球精确引导。从YZ面的投影可以看出,随着保持架兜孔间隙的增大,三种兜孔形状的保持架轴向摆动均逐渐增加,且在不同兜孔间隙下,方形、圆形和球形兜孔保持架的轴向摆动均依次逐渐减小,保持架的轴向摆动与兜孔间隙以及兜孔形状直接相关。

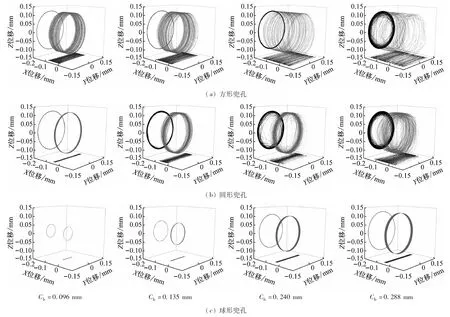
图6 不同兜孔形状以及兜孔间隙下的保持架三维质心轨迹Fig.6 Three-dimensional centroid trajectory of cage under different pocket shapes and pocket gaps

为定量分析不同兜孔形状以及兜孔间隙下各保持架的运动稳定性,本文采用Ghaisas方法[21],即采用涡动速度偏差比(保持架质心运动速度的标准差与平均速度的比)作为保持架稳定性判据,涡动速度偏差比越小,保持架越稳定。不同兜孔形状以及兜孔间隙下各保持架的涡动速度偏差比如图7所示。可以看出,在不同兜孔间隙下,球兜孔保持架的涡动速度偏差比显著低于方形和圆形兜孔保持架,说明球兜孔保持架的稳定性优于方形和圆形兜孔保持架;在间隙比小于1时(兜孔间隙为0.24时,间隙比为1),方兜孔保持架稳定性优于圆兜孔保持架,而在间隙比大于1时,则是圆兜孔保持架更优。

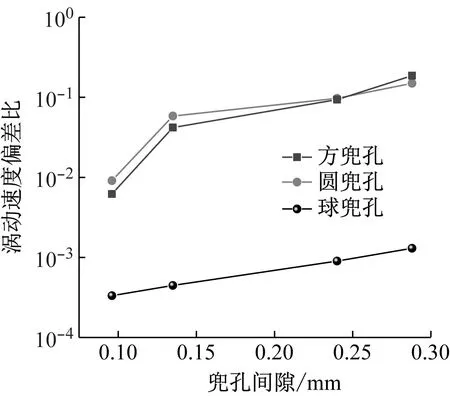
图7 不同兜孔形状及兜孔间隙下的保持架涡动速度偏差比Fig.7 Cage whirl speed deviation ratio under different pocket shapes and pocket gaps

2.2 保持架受力分析

为进一步深入探讨保持架兜孔形状对保持架质心运动的影响,选取兜孔间隙为0.135 mm的保持架进行分析,并将保持架的三维质心运动及受力在保持架方位坐标系中分解,分别对保持架径向涡动半径、圆周涡动速度和轴向摆动以及相应方向的受力进行分析。

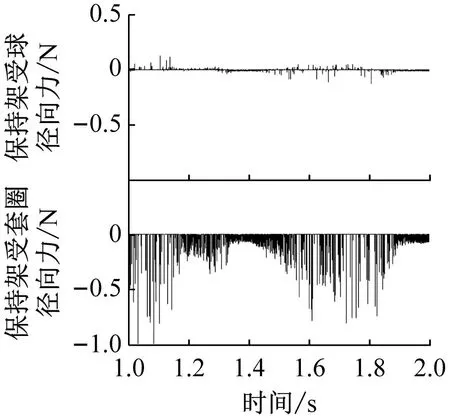
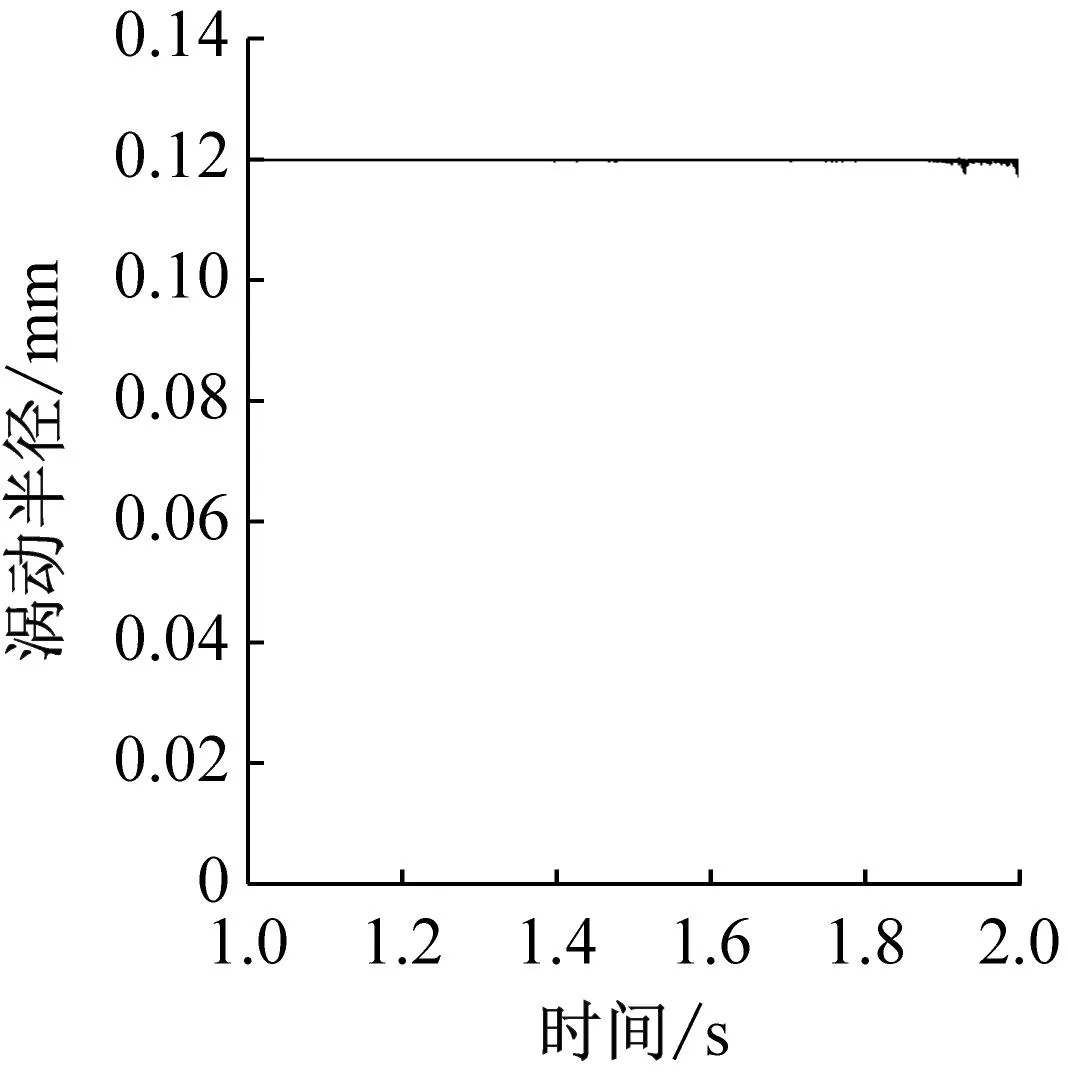
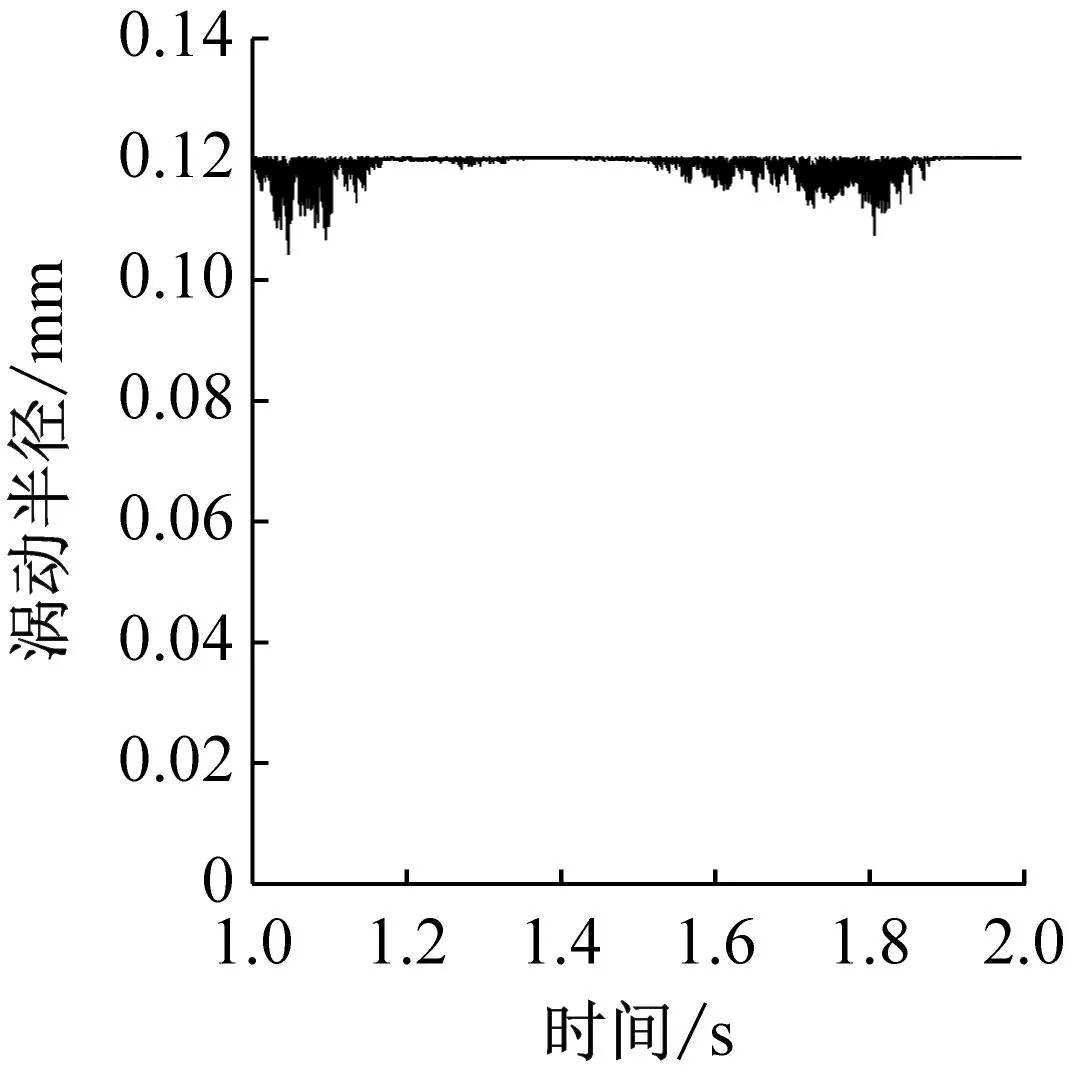
图8和图9分别给出了不同兜孔形状的保持架径向受力以及涡动半径,可以看出方形和圆形兜孔保持架在径向主要受引导套圈的作用力,球对保持架的径向作用力约为套圈的1/10,而球兜孔保持架由于被球限制了运动范围,因此不与套圈发生碰撞。并且可以看出,圆形、方形和球形兜孔保持架在径向的受力逐渐减小,因此,对应的保持架涡动半径的波动也逐渐减小,如图9所示。对比图8和图9可以发现,当保持架与引导套圈发生较大碰撞时,保持架的涡动半径将迅速减小,说明引导套圈对保持架的径向作用力不利于圆形涡动轨迹的形成,而这也是球兜孔保持架质心轨迹非常规则的原因。此外,图9的结果表明方形和圆形兜孔保持架的涡动直径等于套圈引导间隙,而球形兜孔保持架的涡动直径等于兜孔间隙。但是在Gupta、叶振环、刘秀海、张涛等人的圆形兜孔保持架结果中,保持架的质心涡动半径在逐渐增大或始终小于引导间隙,这是因为他们仿真轴承运行的时间较短(小于0.1 s),而动力学程序中保持架的质心位置初值是在轴承中心,仿真0.1 s还不足以使保持架运转到稳定的状态,因此他们的分析虽有参考价值,但由于保持架未运转到稳定状态,结果是不够准确的。

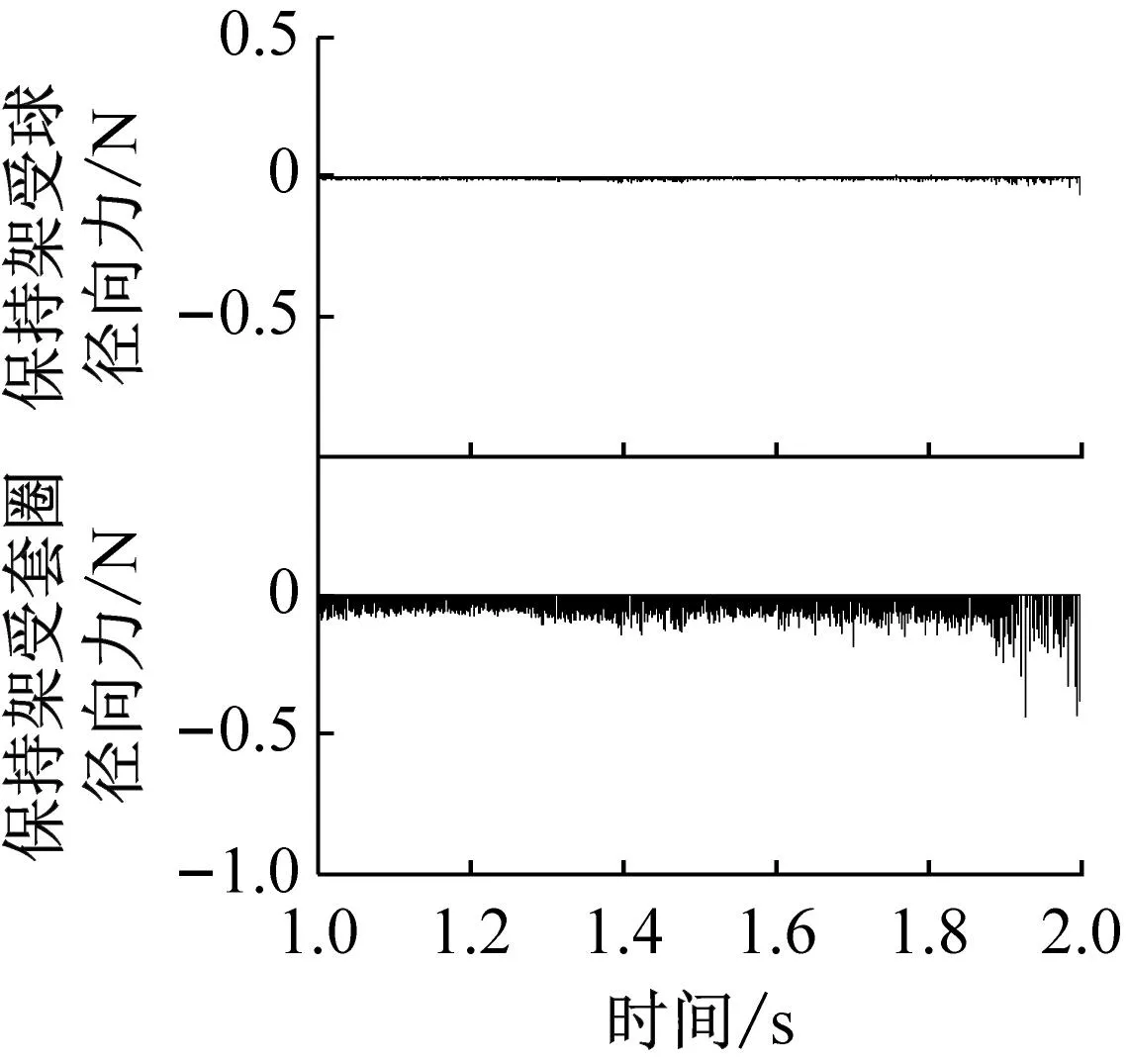
(a) 方形兜孔

(b) 圆形兜孔

(a) 方形兜孔

(b) 圆形兜孔

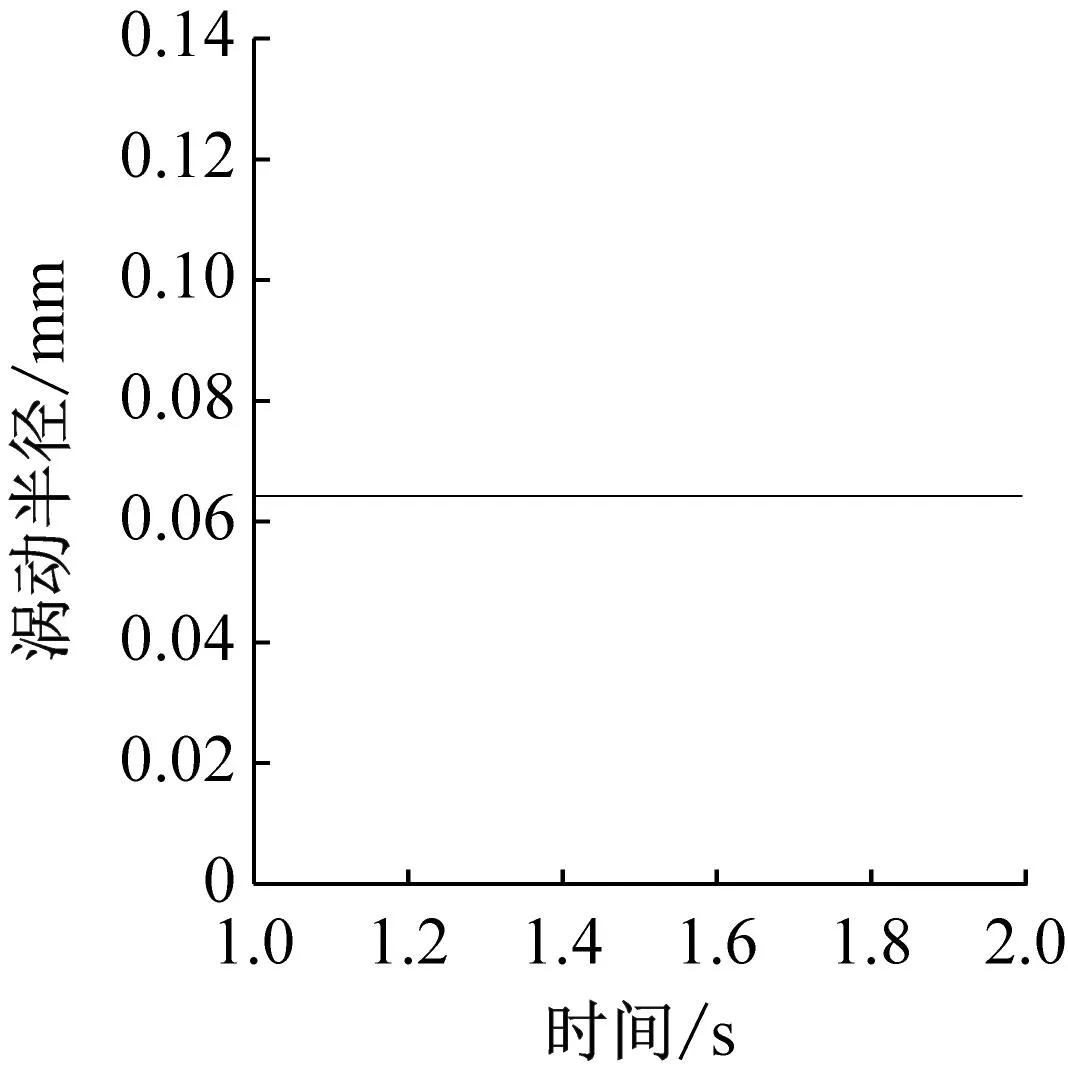
(c) 球形兜孔图9 不同兜孔形状保持架的涡动半径Fig.9 Cage whirl radius of different pockets

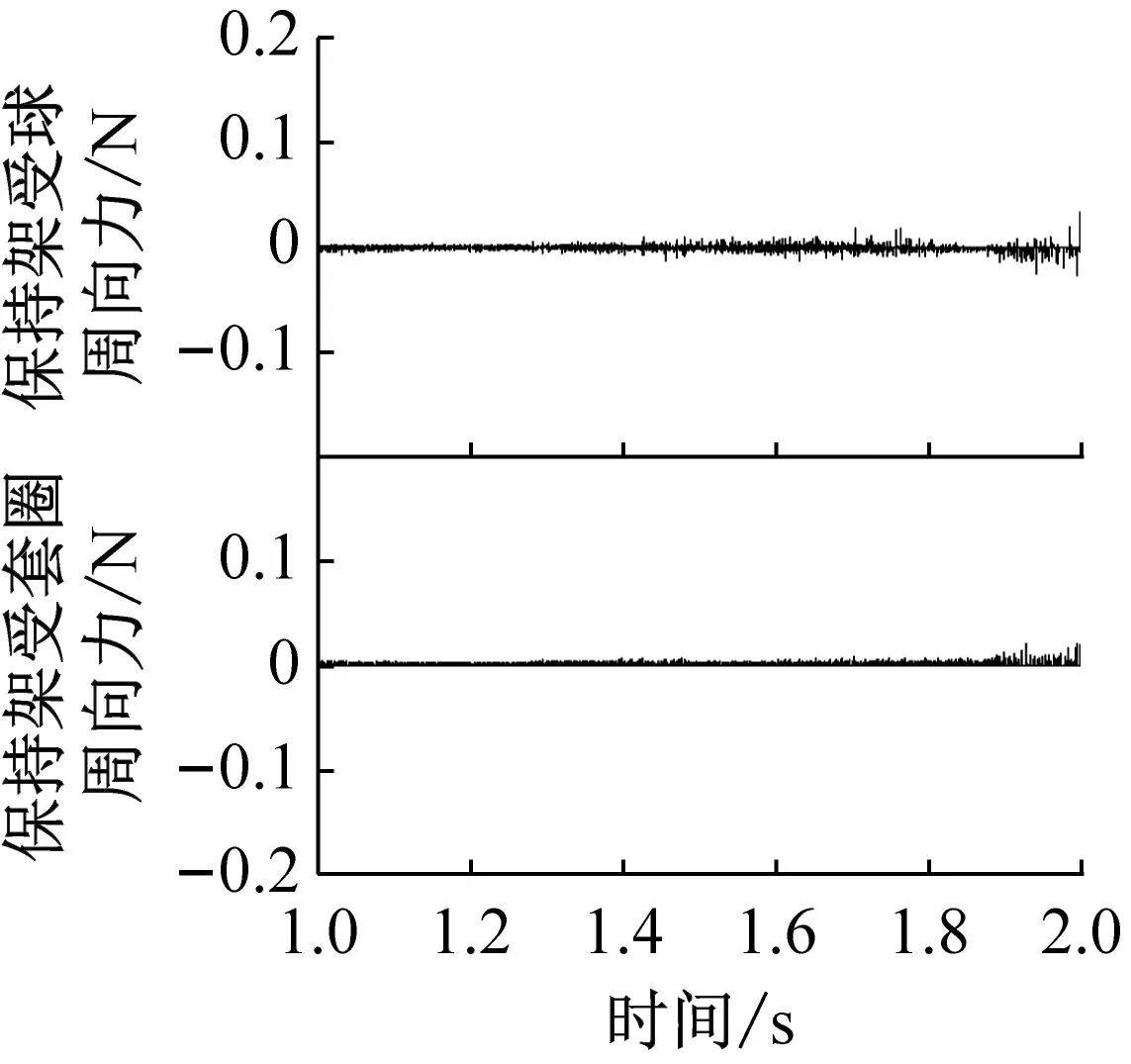
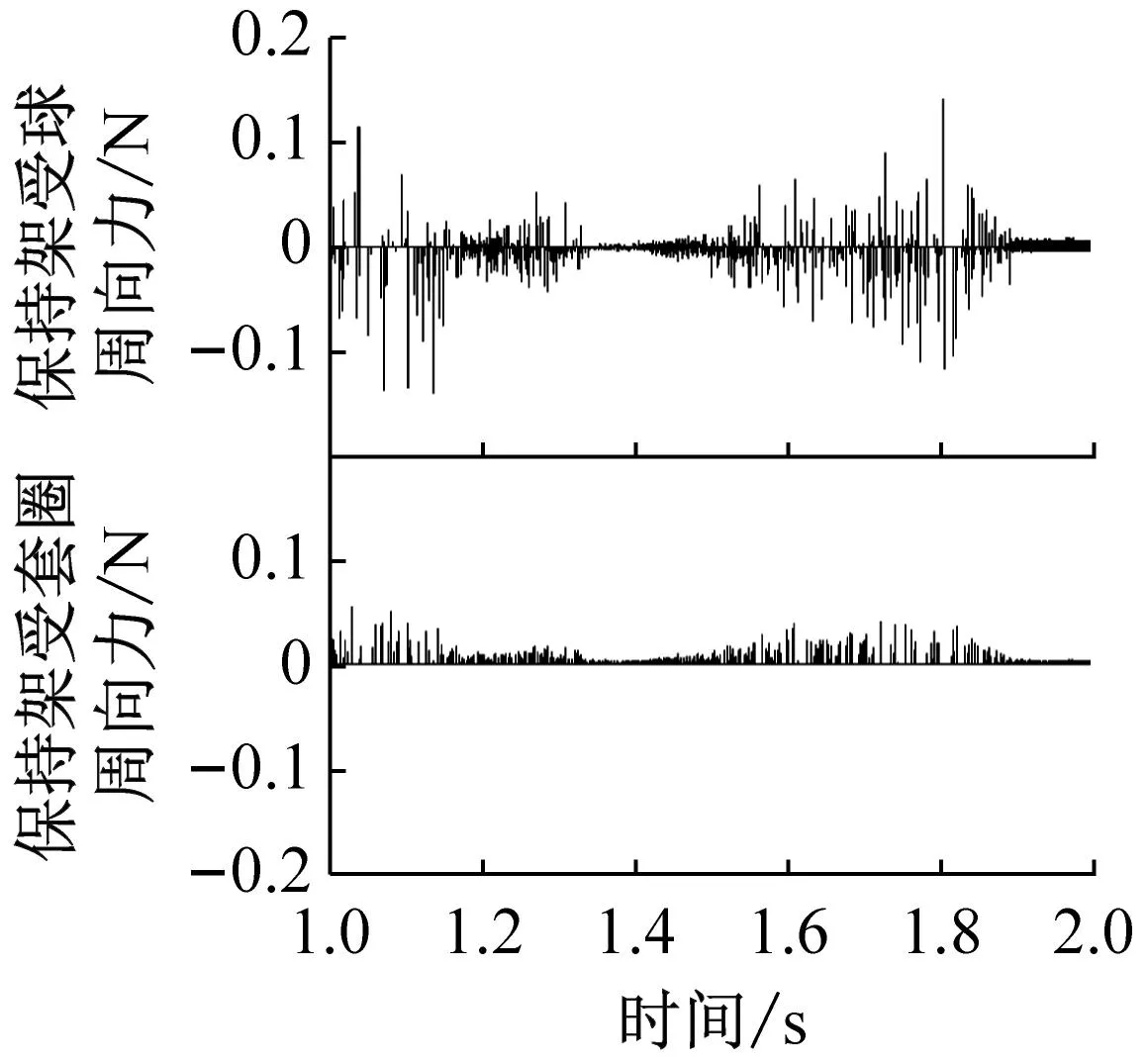
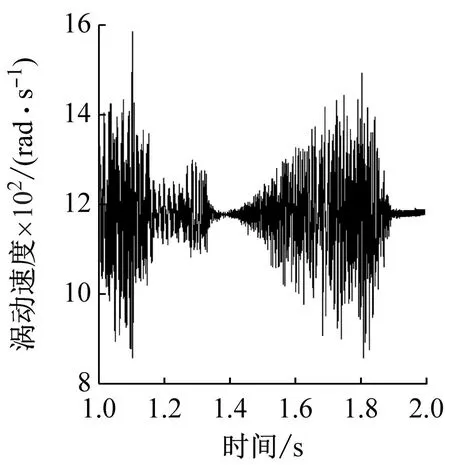
图10和图11分别给出了不同兜孔形状的保持架周向受力以及涡动速度,需要指出的是由于保持架方位坐标系的Yca轴与保持架涡动方向相反,因此数值为正的周向力是阻碍保持架的涡动的,而数值为负的周向力驱动着保持架的涡动。从图10可以看出,对于方兜孔和圆兜孔,保持架在周向主要承受钢球的作用力,而引导套圈对保持架作用力较小且始终是阻力,这是因为保持架是由固定的外圈引导的,且外圈对保持架周向作用力是由摩擦力产生的;而球对保持架的周向作用力主要由碰撞力承担,当球超前于保持架的运动时,球驱动着保持架的涡动,当球滞后于保持架的运动时,球阻碍着保持架的涡动。图10中球对保持架的作用力有正有负,因此时而驱动时而阻碍并维持着保持架的涡动速度处于动态平衡态。由于球与圆兜孔保持架的冲击力较大,这也就导致了图11中保持架的涡动速度波动较大,而对于球兜孔保持架则由于碰撞冲击力很小,因此球兜孔保持架的涡动速度也就非常平稳。

(a) 方形兜孔

(b) 圆形兜孔

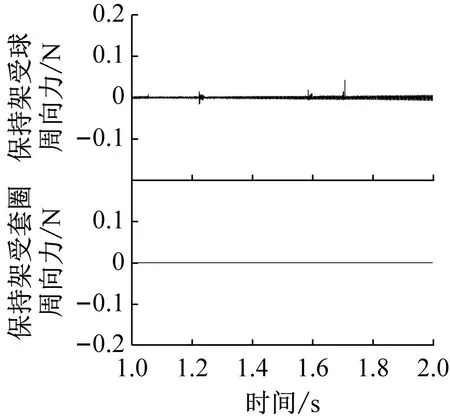
(c) 球形兜孔图10 不同兜孔形状保持架的周向受力Fig.10 Circumferential force on the cage of different pockets

(b) 圆形兜孔

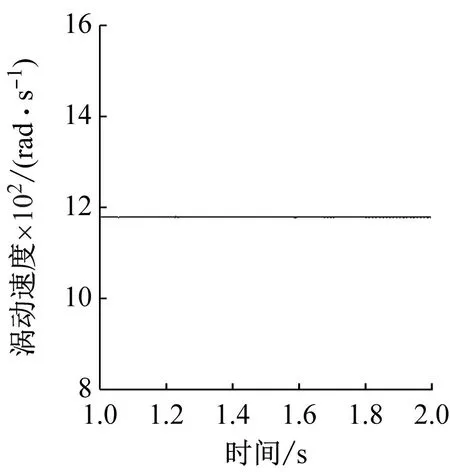
(c) 球形兜孔图11 不同兜孔形状保持架的涡动速度Fig.11 Cage whirl speed of different pockets

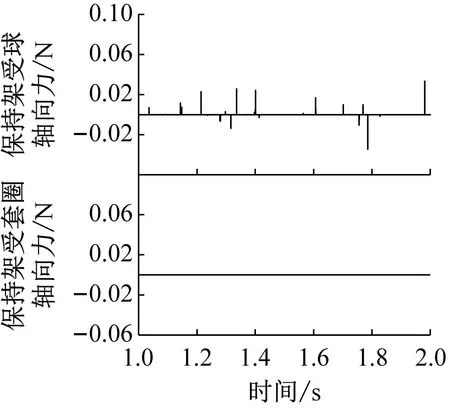
图12和图13分别给出了不同兜孔形状的保持架轴向受力以及轴向摆动位移,可以看出,在轴向上,保持架仅受球的作用力(对于方兜孔和圆兜孔保持架还受引导套圈的摩擦力在轴向的分量,但由于保持架涡动速度相对于轴向摆动速度大得多,因此摩擦力在轴向的分量约为10-6N级,可忽略不计),因此保持架在轴向上的摆动仅与球对其作用力相关。与径向力和周向力类似,球兜孔保持架在轴向受力也非常小,对应的保持架轴向摆动量也是很小的。而对于方兜孔和圆兜孔,方兜孔保持架在轴向受力大小和频率均小于圆兜孔保持架,对应的方兜孔保持架轴向摆动频率小于圆兜孔保持架,但是摆动范围却较圆兜孔更大,这是因为圆兜孔保持架所受轴向力虽然更大,但是频率也更高,当保持架还来不及沿轴向正向(负向)产生较大的位移时,负(正)的轴向作用力就使得保持架沿负(正)向运动了,使得圆兜孔保持架在轴向处于一个较稳定的动态平衡状态。

(a) 方形兜孔

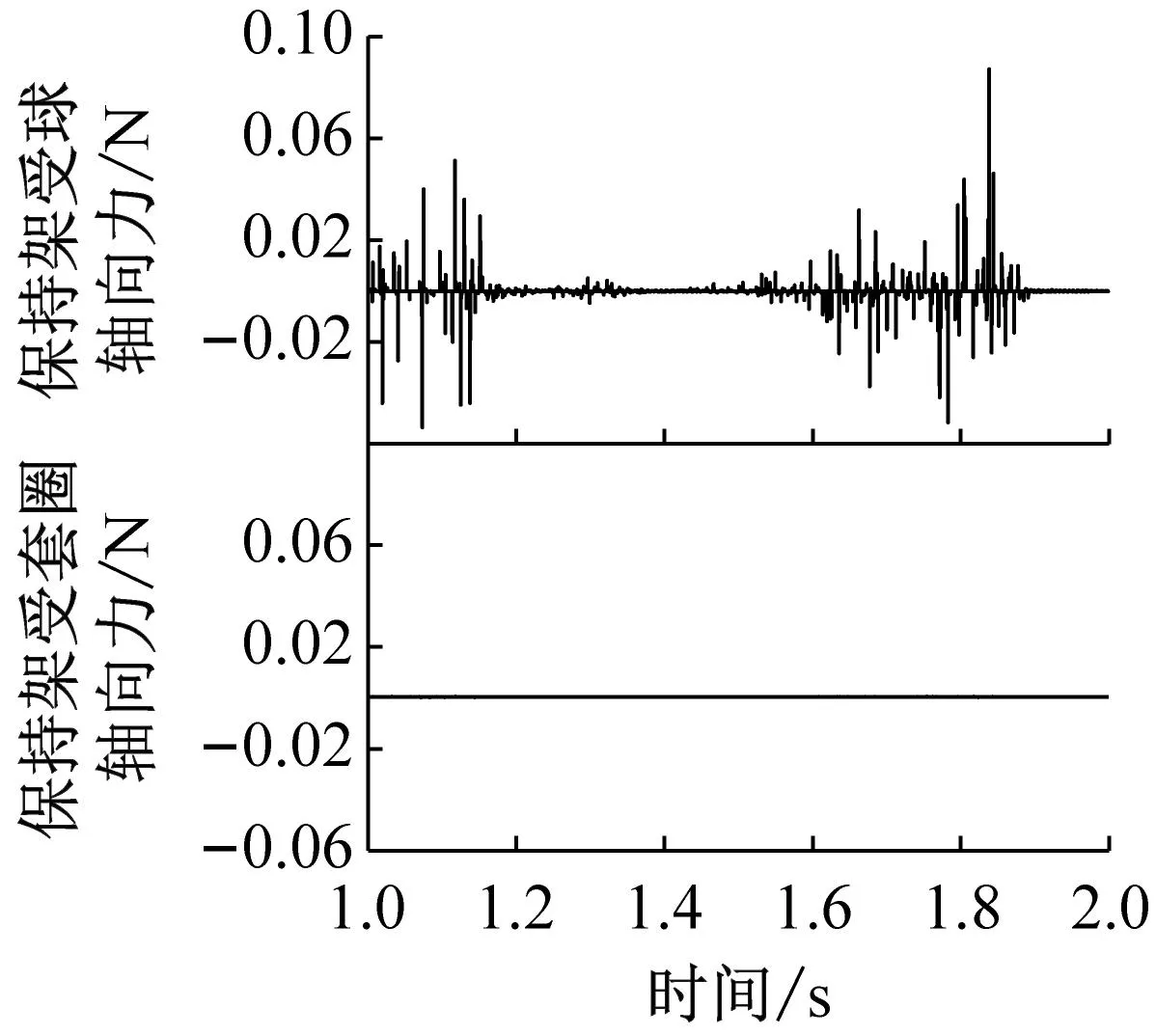
(b) 圆形兜孔

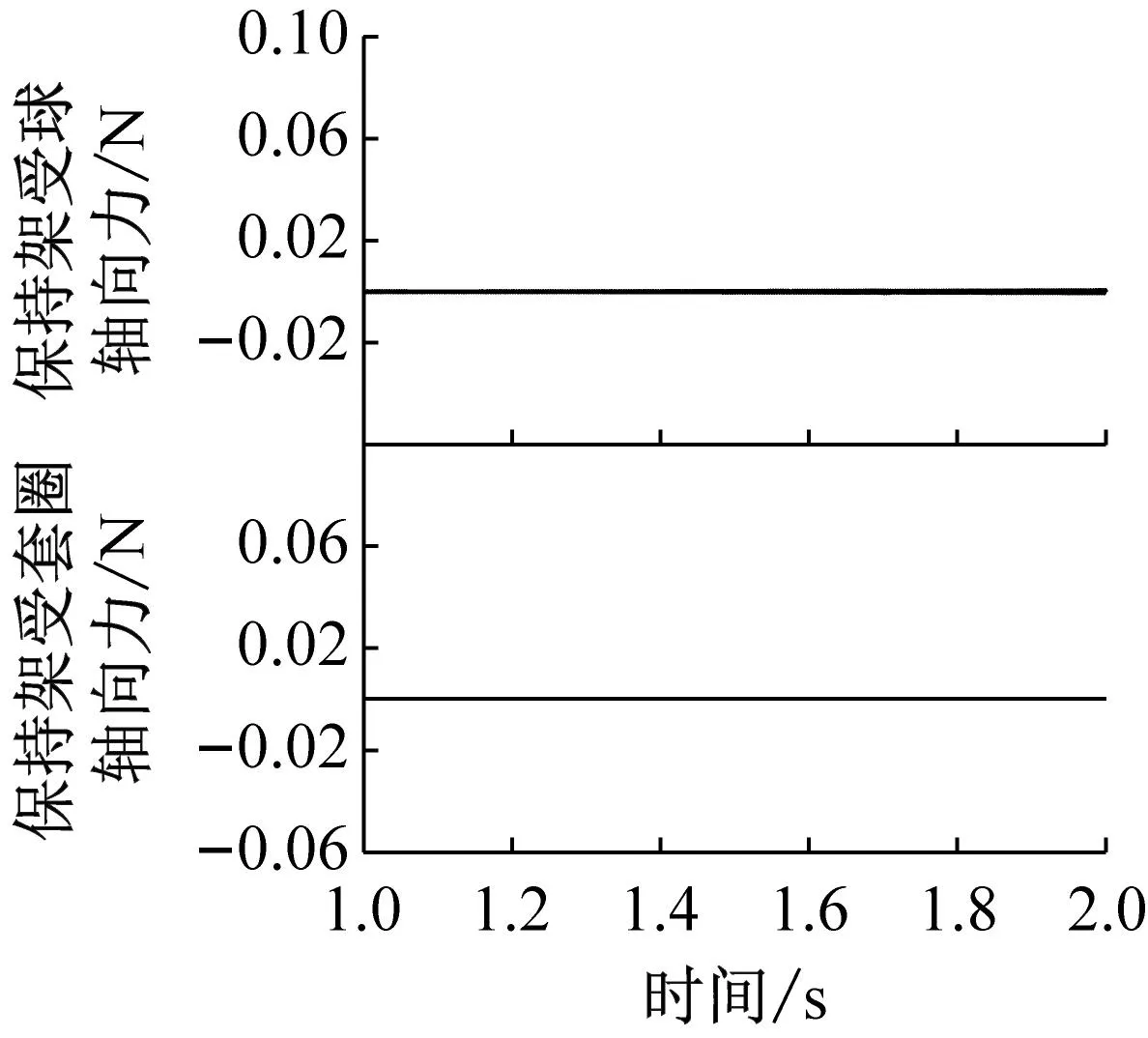
(c) 球形兜孔图12 不同兜孔形状保持架的轴向受力Fig.12 Axial force on the cage of different pockets

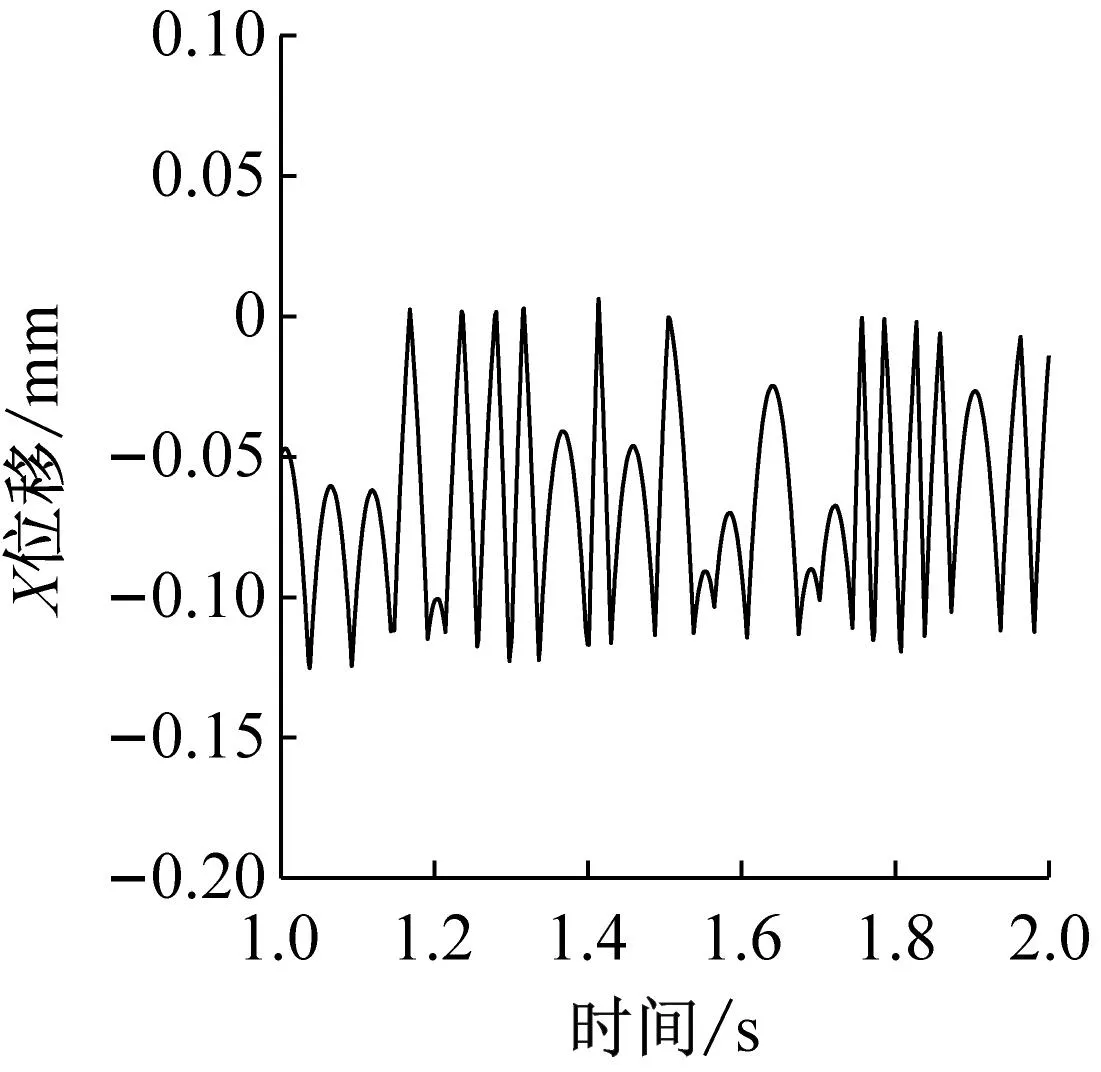
(a) 方形兜孔

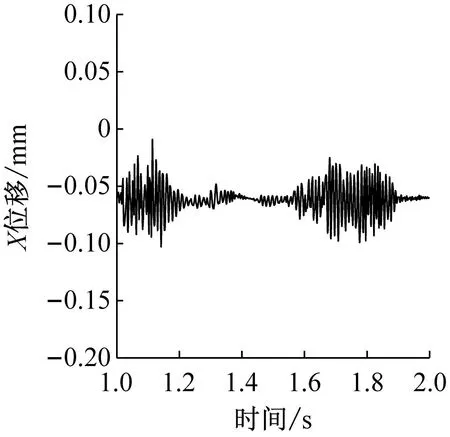
(b) 圆形兜孔

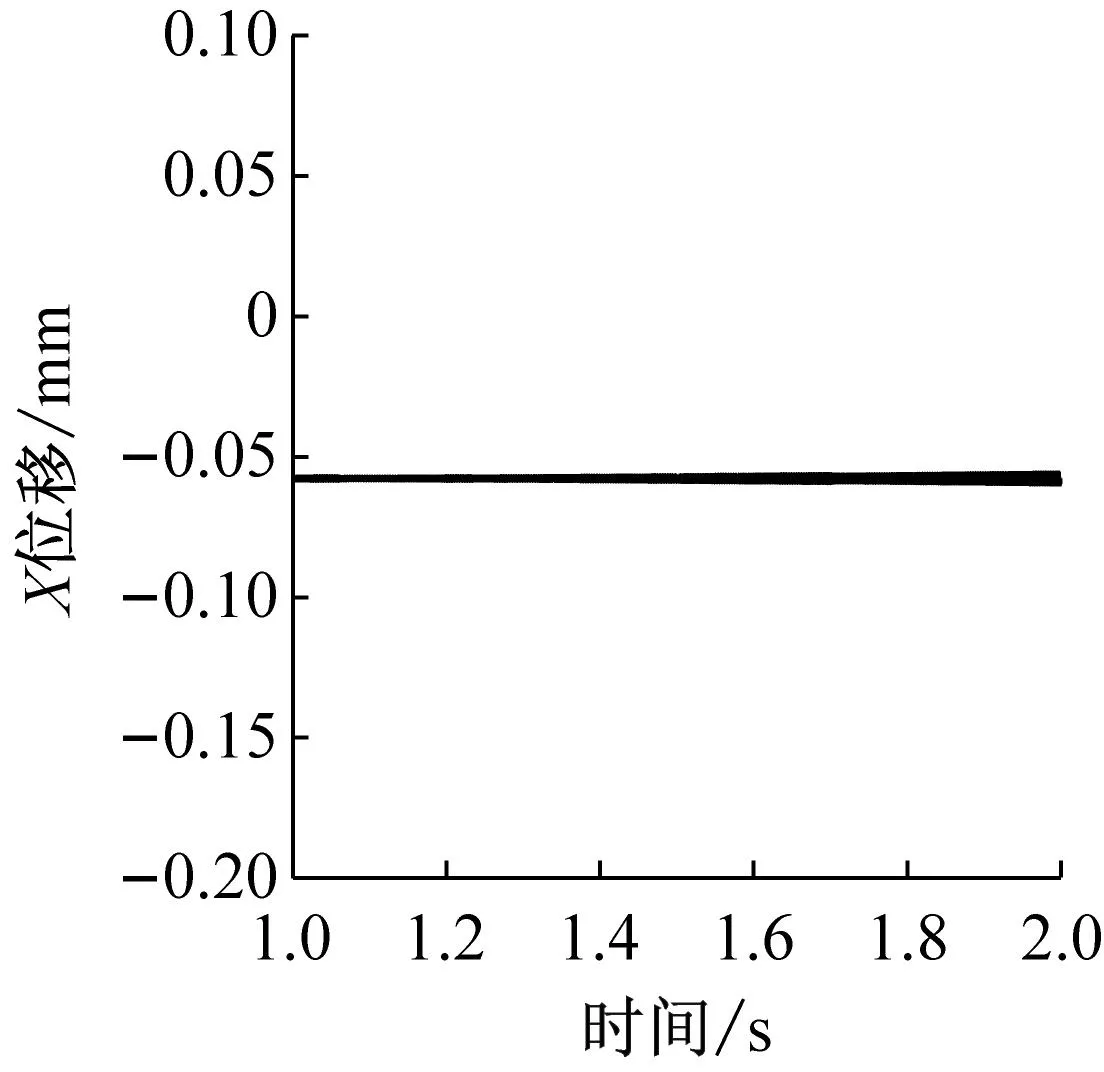
(c) 球形兜孔图13 不同兜孔形状保持架的轴向摆动Fig.13 Cage axial motion of different pockets

2.3 保持架磨损分析

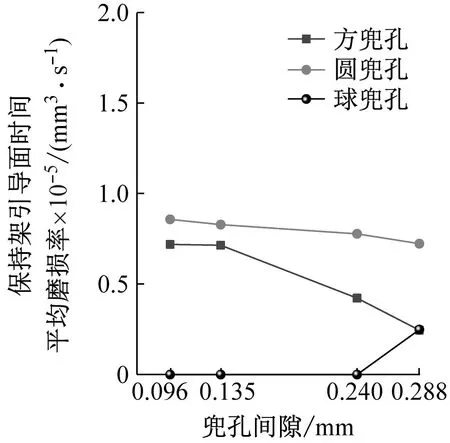
图14为不同兜孔形状保持架兜孔面、引导面以及总的时间平均磨损率,保持架总的时间平均磨损率是兜孔面和引导面磨损率之和。时间平均磨损率表示的是一段时间内磨损量的平均值。可以看出,随着保持架兜孔间隙的增大,三种兜孔形状的保持架兜孔时间平均磨损率逐渐降低,且圆兜孔保持架的兜孔时间平均磨损率远大于方兜孔和圆兜孔保持架。而对于保持架引导面的时间平均磨损率,当兜孔间隙小于引导间隙时,球兜孔保持架不与套圈相接触,因此引导面的时间平均磨损率为零;当兜孔间隙大于引导间隙时,球兜孔保持架引导面开始出现磨损;圆兜孔和方兜孔保持架引导面的时间平均磨损率随着兜孔间隙的增加逐渐减小,且圆兜孔保持架引导面的时间平均磨损率始终大于方兜孔;此外,对比保持架兜孔面与引导面的磨损可以看出,球兜孔保持架兜孔面的磨损始终远大于引导面,而方兜孔和圆兜孔保持架引导面的磨损始终大于兜孔面的磨损,再一次说明了球兜孔保持架是由球引导的,而方兜孔和圆兜孔保持架则是由引导套圈引导的。从图14(c)可以看出三种兜孔形状的保持架总的磨损均随着兜孔间隙的增加而减小,这与图7所反映的保持架稳定性是相反的,说明保持架越稳定,保持架的磨损率反而更低。这是因为当保持架处于稳定的涡动状态时,保持架与球以及引导套圈之间的作用力虽然比较小,但是作用频率却高得多,因此接触磨损的时间更长,保持架的磨损反而更大。所以,保持架的设计需要综合考虑保持架的稳定性和磨损,不能仅单独地追求更好的保持架稳定性或更低的磨损率。

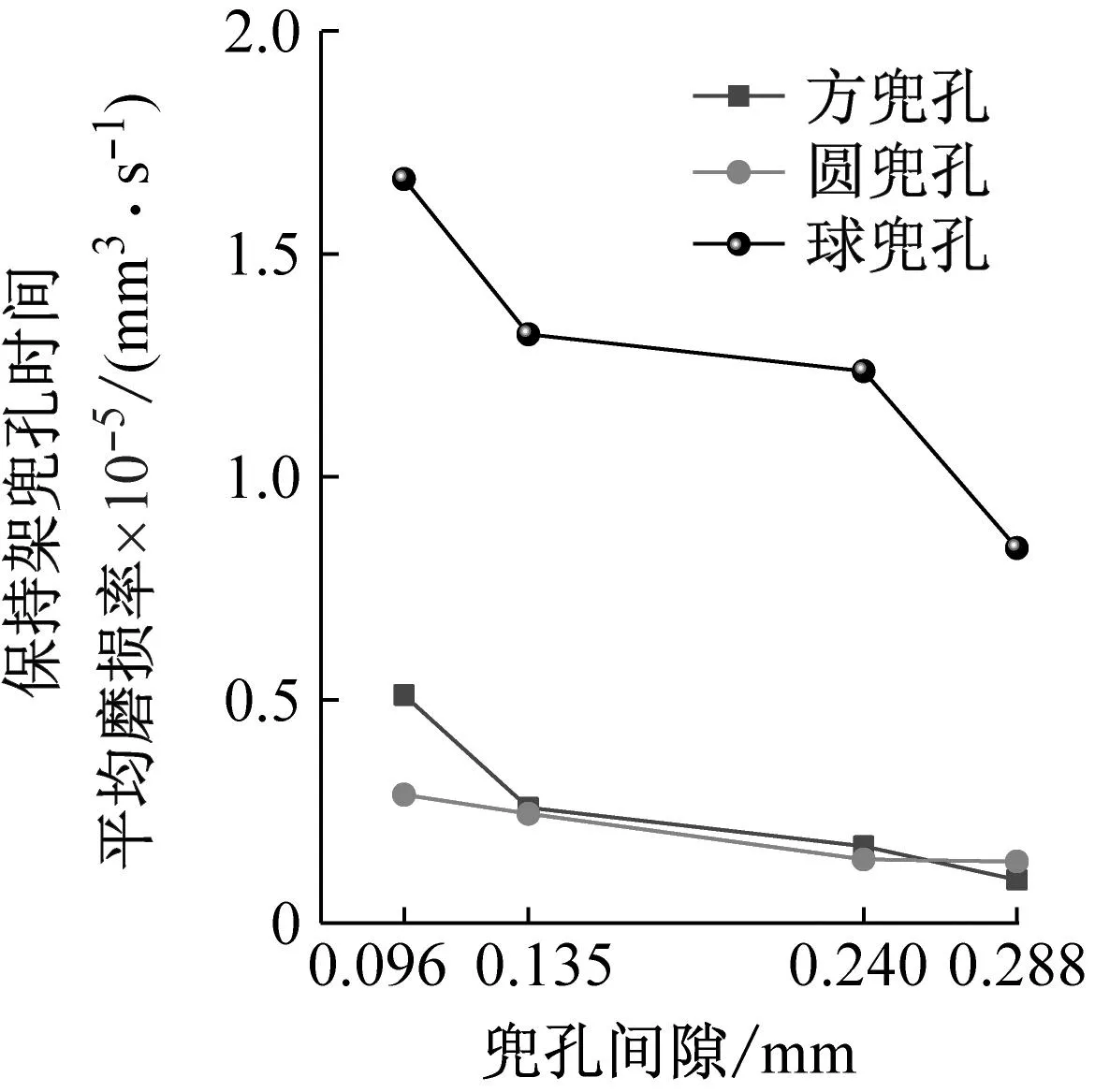
(a) 方形兜孔

(b) 圆形兜孔

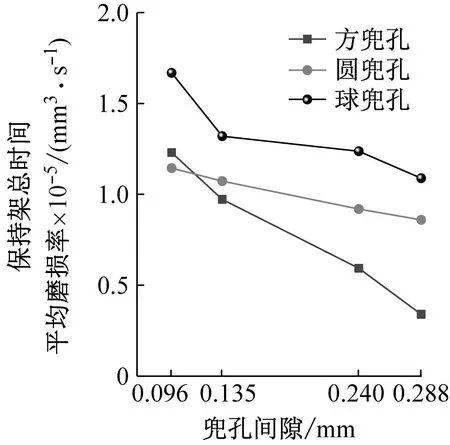
(c) 球形兜孔图14 不同兜孔形状保持架的时间平均磨损率Fig.14 Cage time-average wear rate of different pockets

3 试验验证

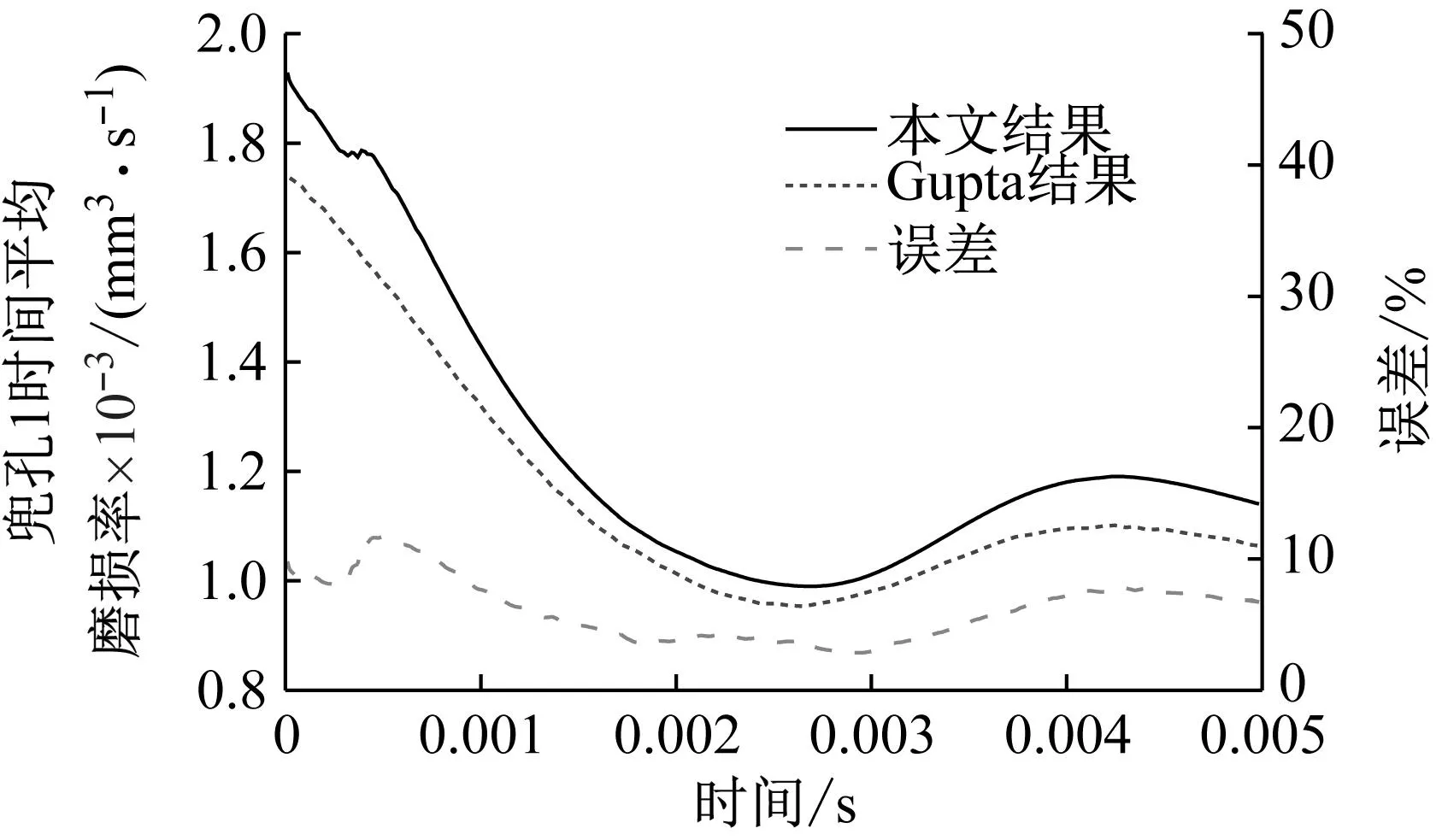
为了验证本文提出的三种兜孔形状的保持架动力学数值仿真模型的正确性,与Gupta的2号角接触球轴承的算例对比验证圆形兜孔保持架动力学模型得程序。轴承的工况为内圈转速30 000 r/min,推力载荷为5 000 N,旋转径向载荷为4 000 N。本文程序1号兜孔的磨损率及保持架质心轨迹与Gupta的结果如图15所示。本文程序磨损率与Gupta结果趋势一致,大小基本相等,最大误差不超过12%,且保持架质心轨迹与Gupta也基本一致,因此本文圆柱形兜孔保持架动力学程序正确性和可靠性得到了验证。方形兜孔和球形兜孔保持架动力学结果报道较少,下面将用课题组设计的高速角接触球轴承保持架动态特性试验机进行试验验证。

(a) 磨损率

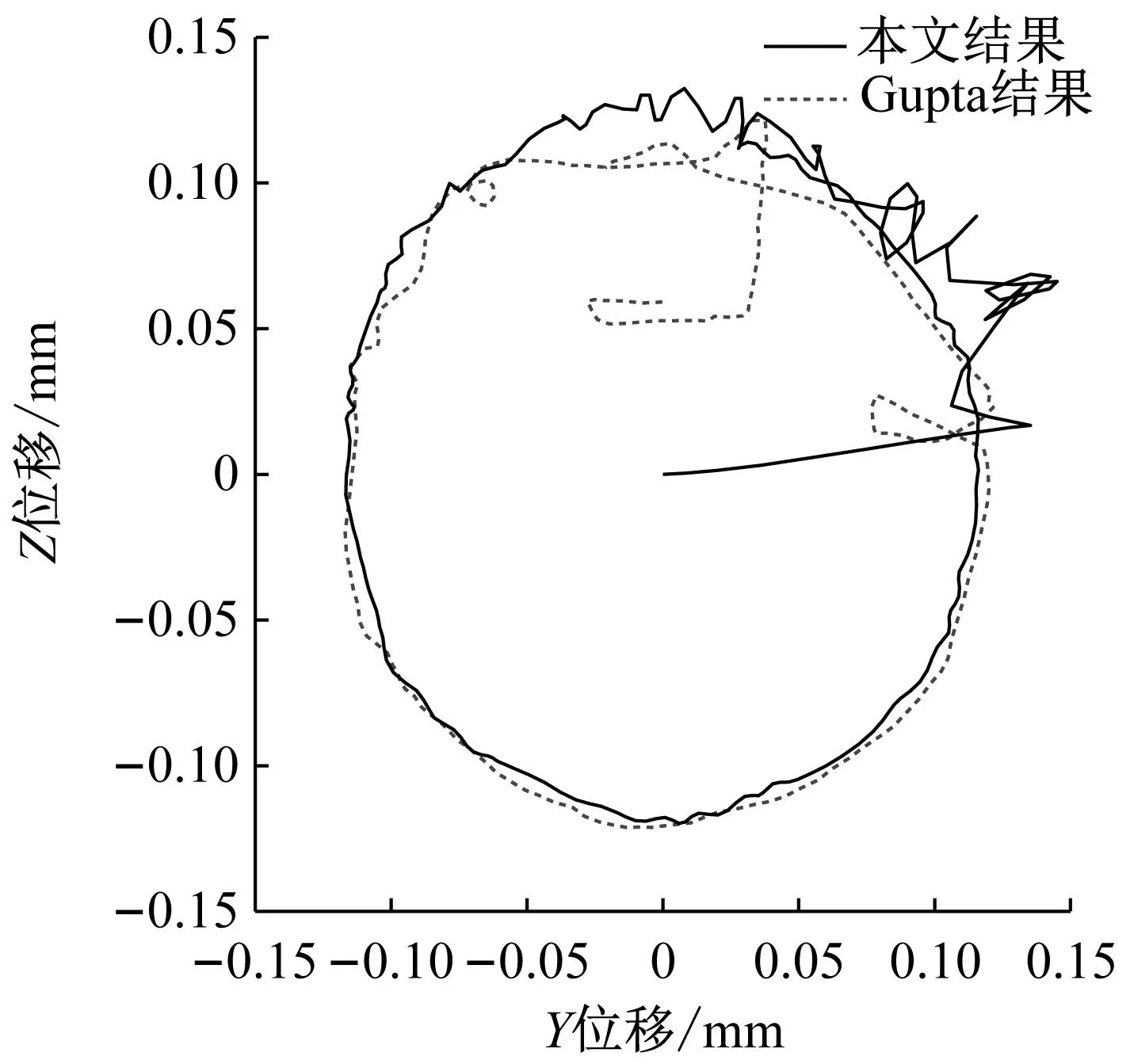
(b) 质心轨迹图15 本文圆柱兜孔保持架动力学结果与Gupta结果对比Fig.15 Comparison between the cylindrical pocket cage dynamic results of current model and Gupta’s model

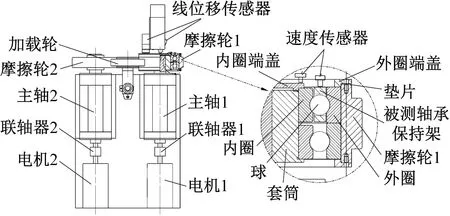
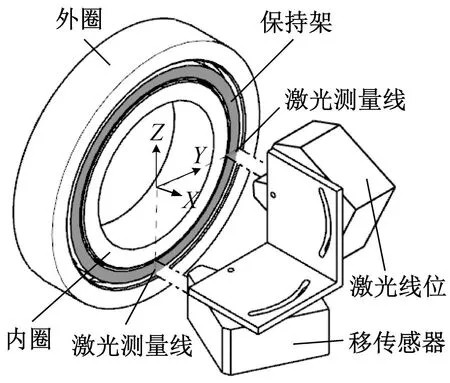
为进一步验证本文提出的三种兜孔形状的保持架动力学数值仿真模型的正确性,采用课题组设计的高速角接触球轴承保持架动态特性试验机[22-23]分别对这三种兜孔形状的保持架进行试验探究,试验机的结构图如图16所示。电机1通过联轴器直接带动被试轴承内圈旋转,电机2通过带动摩擦轮2、加载轮以及摩擦轮1,从而带动被试轴承外圈旋转,从而实现被试轴承内外圈在一定转速范围内任意同向或反向旋转。选用两个如图16所示的LJ-G015K激光线位移传感器测量保持架的三维质心轨迹,其X轴测量范围为(高度)15±2.3 mm,Z轴测量范围距离7 mm;激光线位移传感器打出来的激光线是由一排激光点组成的,其中有效测量点为800个,两相邻激光点的间距恒定为10 μm,即800个点中700个点为有效数据,两端各50点为无效数据,在有效测量范围内被测物体超量程时显示为999.999的无效数据,根据无效点的个数变化情况及各个点之间的距离即可算出被测物体X向的位移,被测物体Z或Y向的位移可直接由得到的有效数据取平均值计算,由此就可以在不改变轴承结构的情况下同步测得保持架的径向和轴向位移,也就是得到保持架的空间三维质心轨迹。被试轴承参数如表2所示。轴承内圈转速为1 000 r/min,外圈固定,轴向预载荷为100 N。需要说明的是,由于激光线位移传感器尺寸的限制,试验所用的轴承较大,本试验主要用于验证所建立数值仿真模型的正确性。

(a)

(b)

(c)

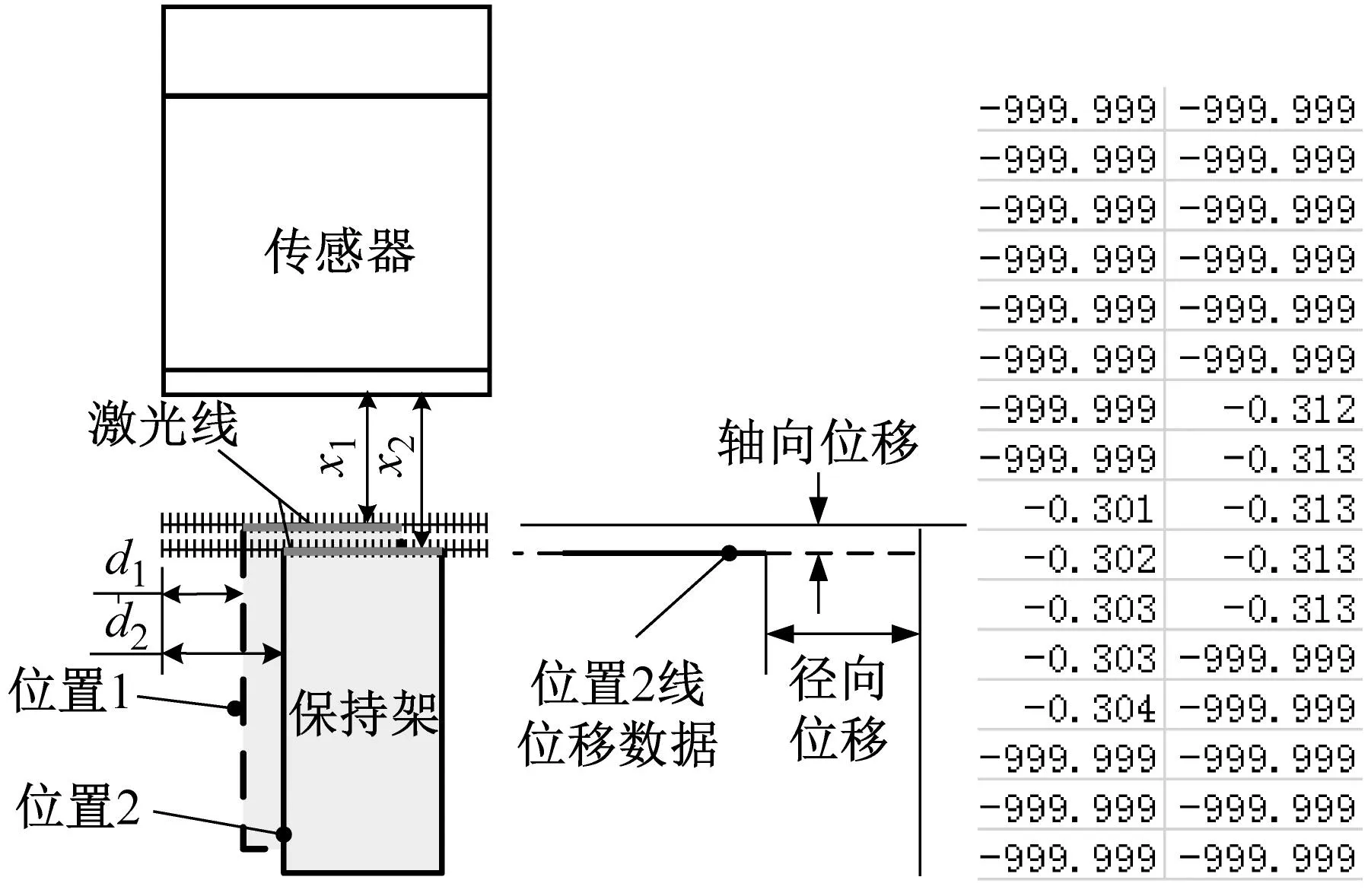
(d)图16 试验机结构图以及测量原理图Fig.16 Test machine structure diagram and measurement principle diagram

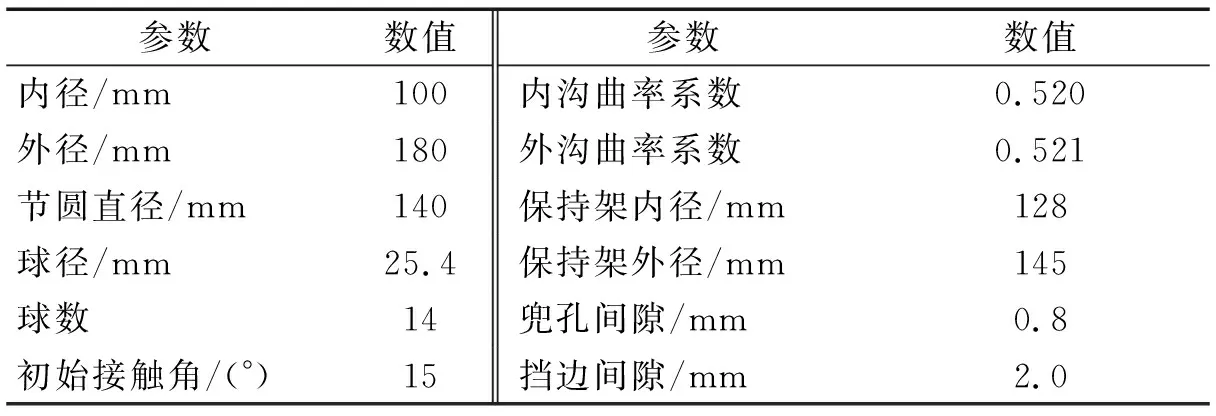
表2 被试轴承几何参数Tab.2 Geometric parameters of the tested bearing

图17～19为数值仿真和试验得到的三种兜孔形状保持架的三位质心轨迹以及Y向位移响应,从图中可以看出,三种兜孔形状的保持架质心轨迹形状和轨迹半径都与仿真结果接近,且从Y向位移响应的结果看,仿真结果和试验结果也保持较好的同步性,说明仿真和试验得到的保持架涡动速度是一致的,从而在保持架质心位移和速度两个方面验证了仿真结果的可靠性与准确性。

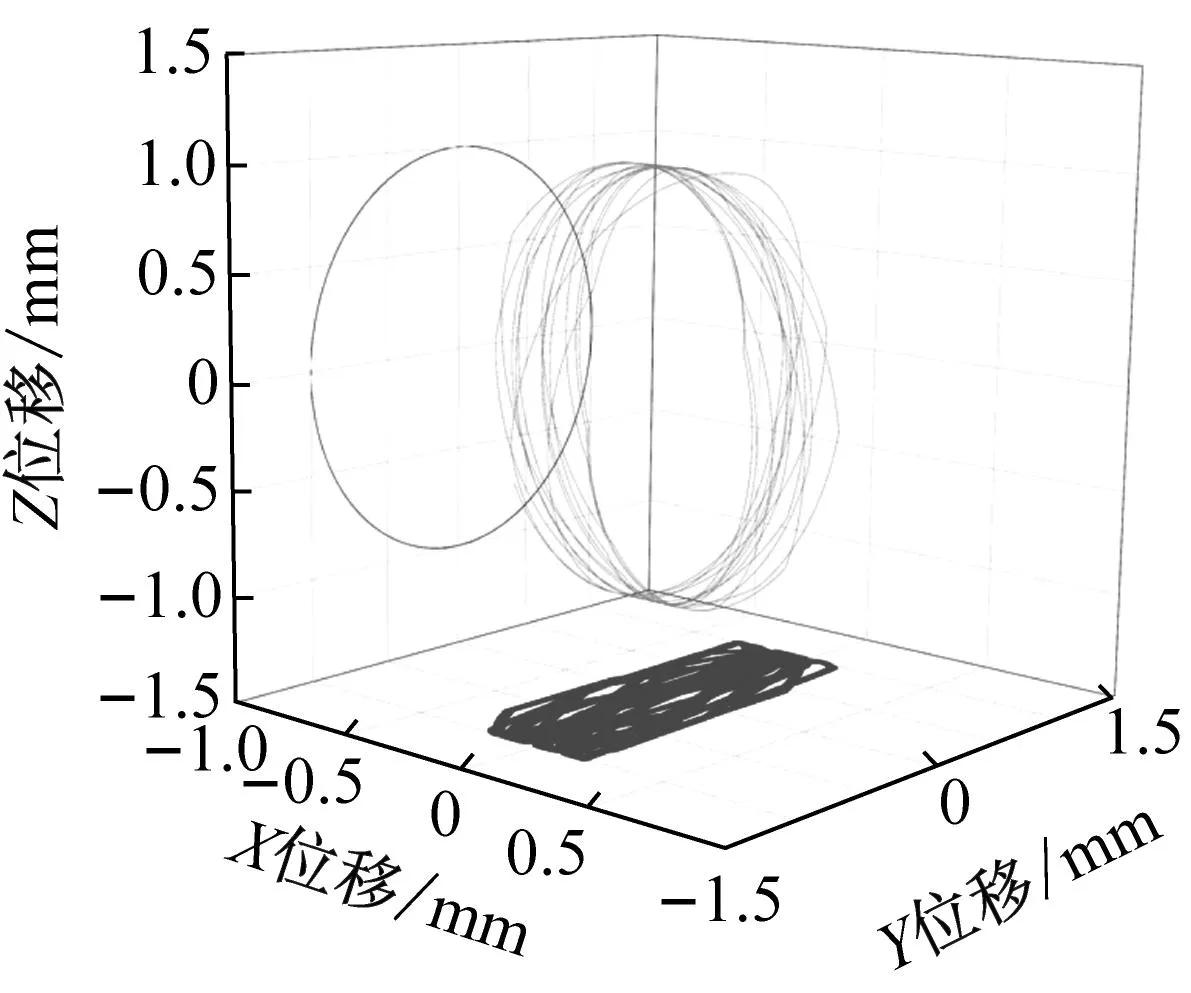
(a) 数值仿真三维质心轨迹

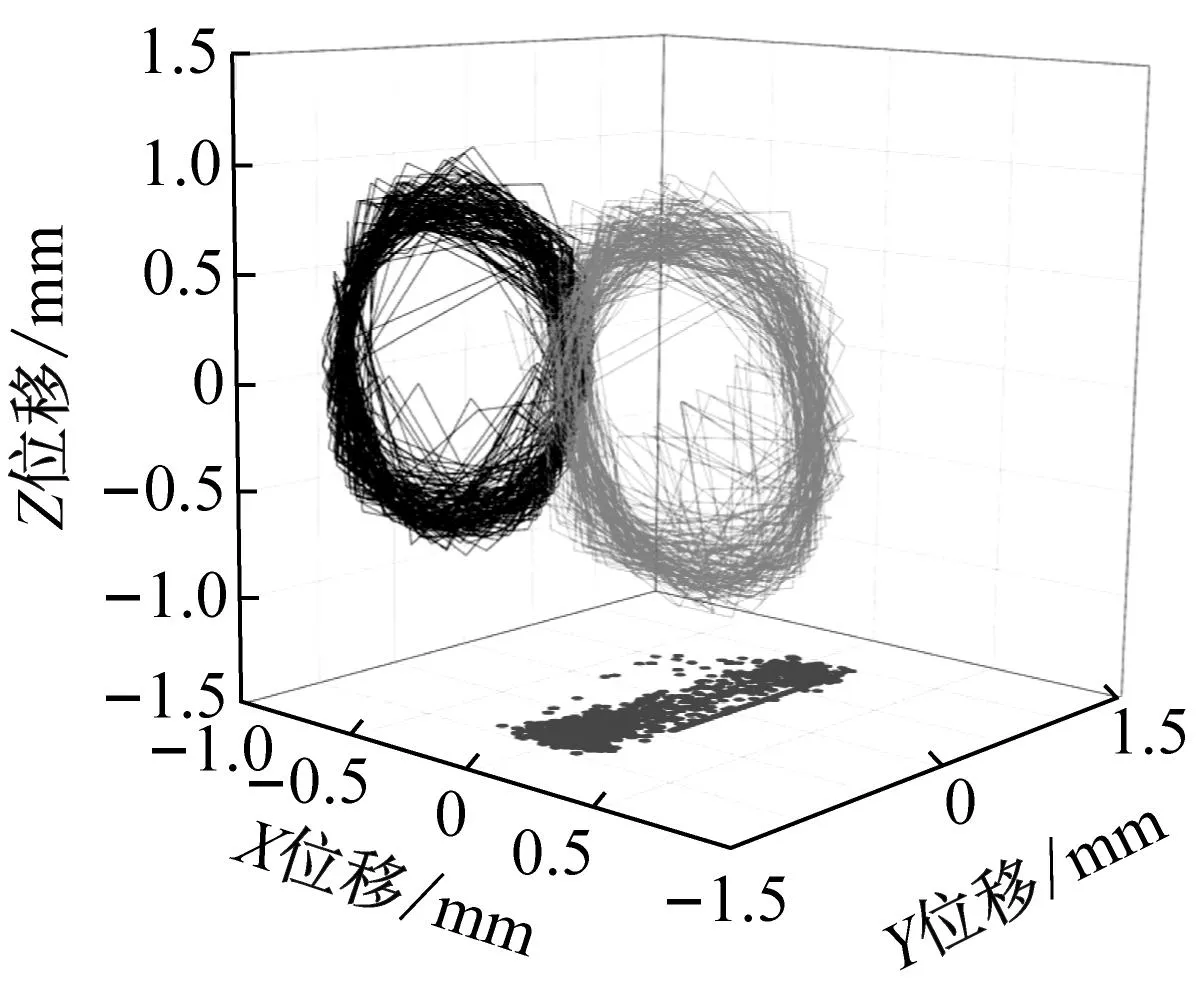
(b) 试验三维质心轨迹

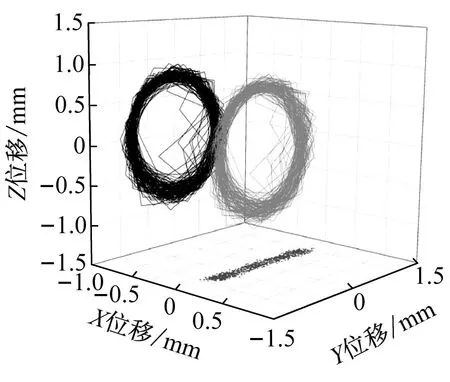
(b) 试验三维质心轨迹

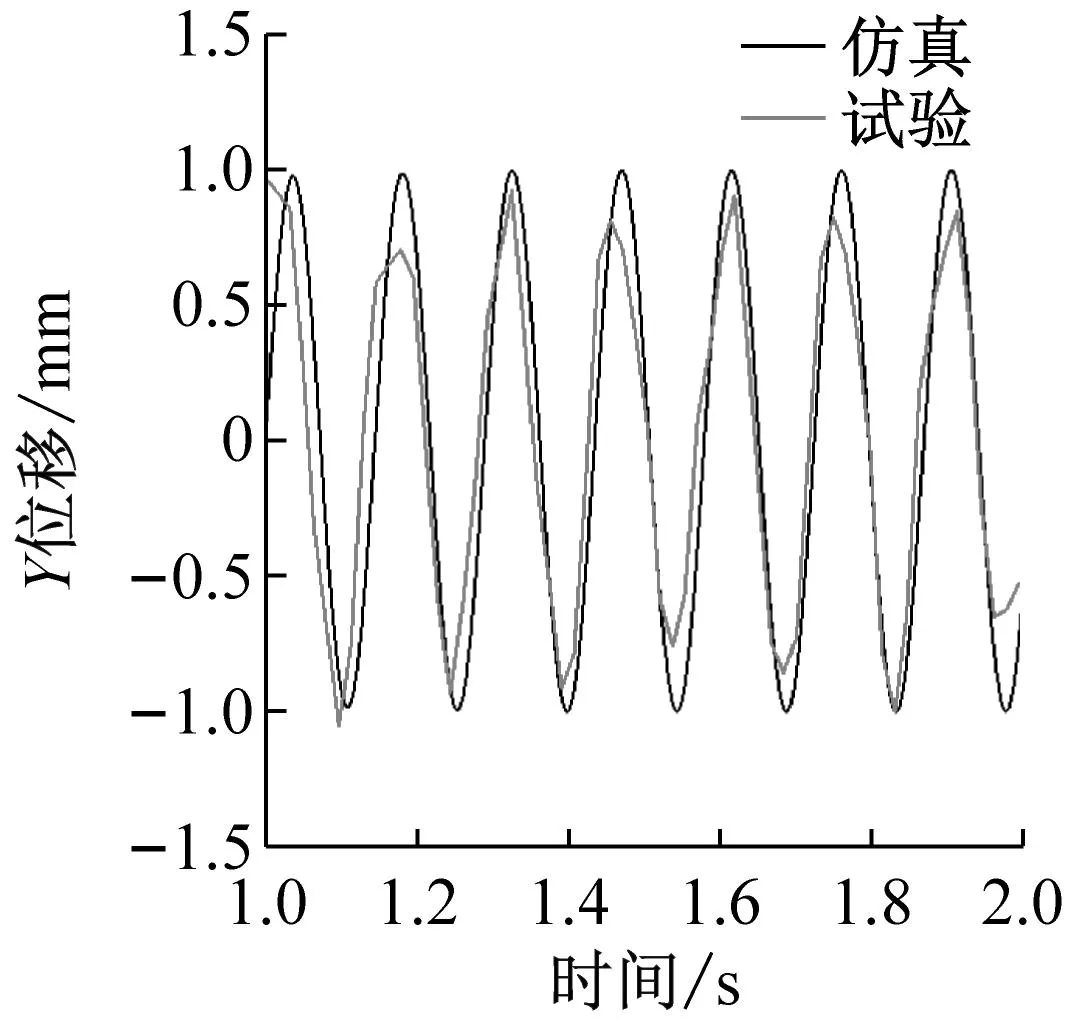
(c) Y方向位移响应图18 圆兜孔保持架质心运动Fig.18 Cylindrical pocket cage motion

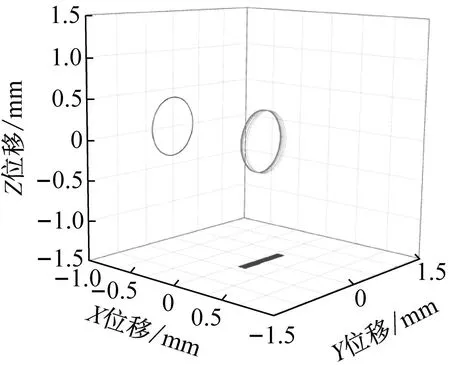
(a) 数值仿真三维质心轨迹

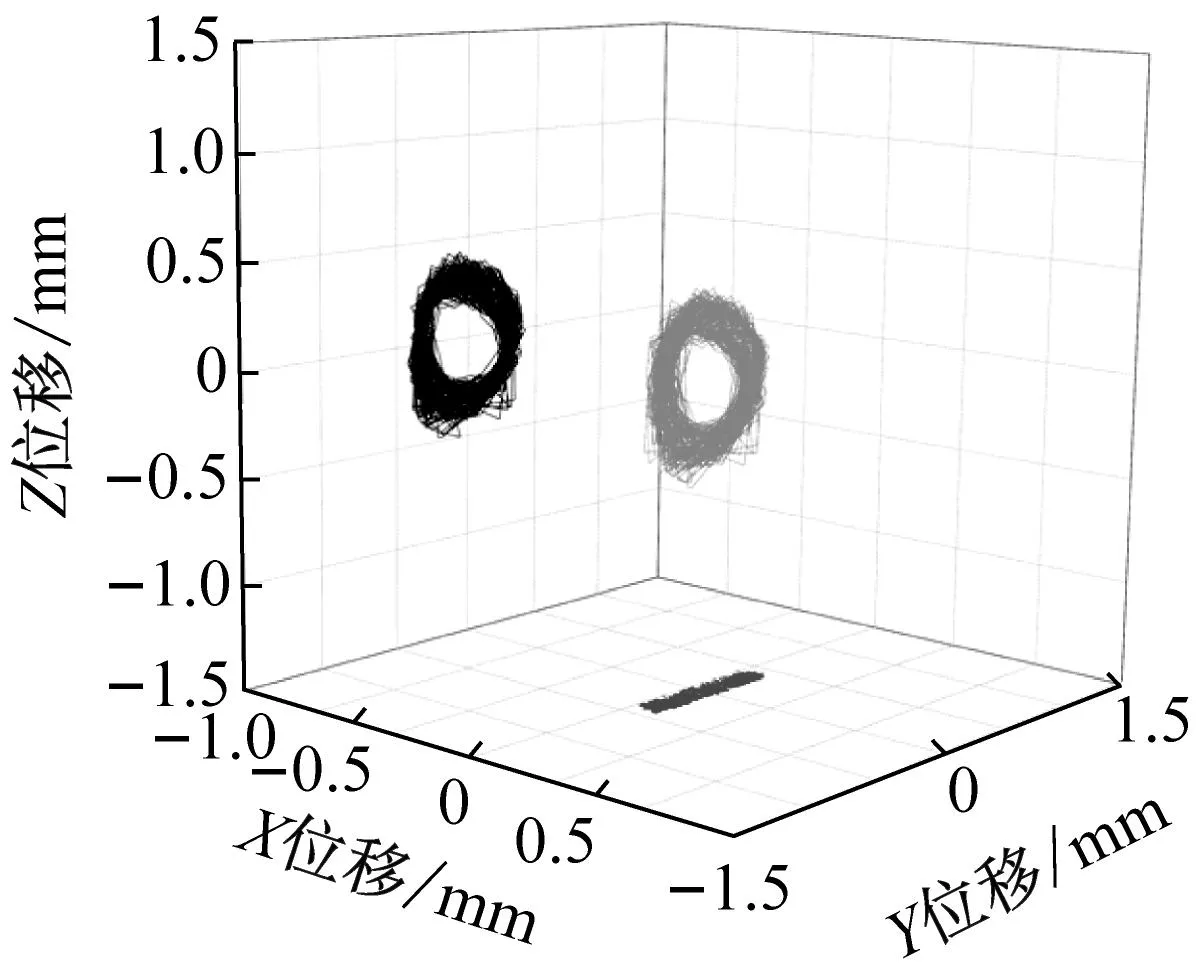
(b) 试验三维质心轨迹

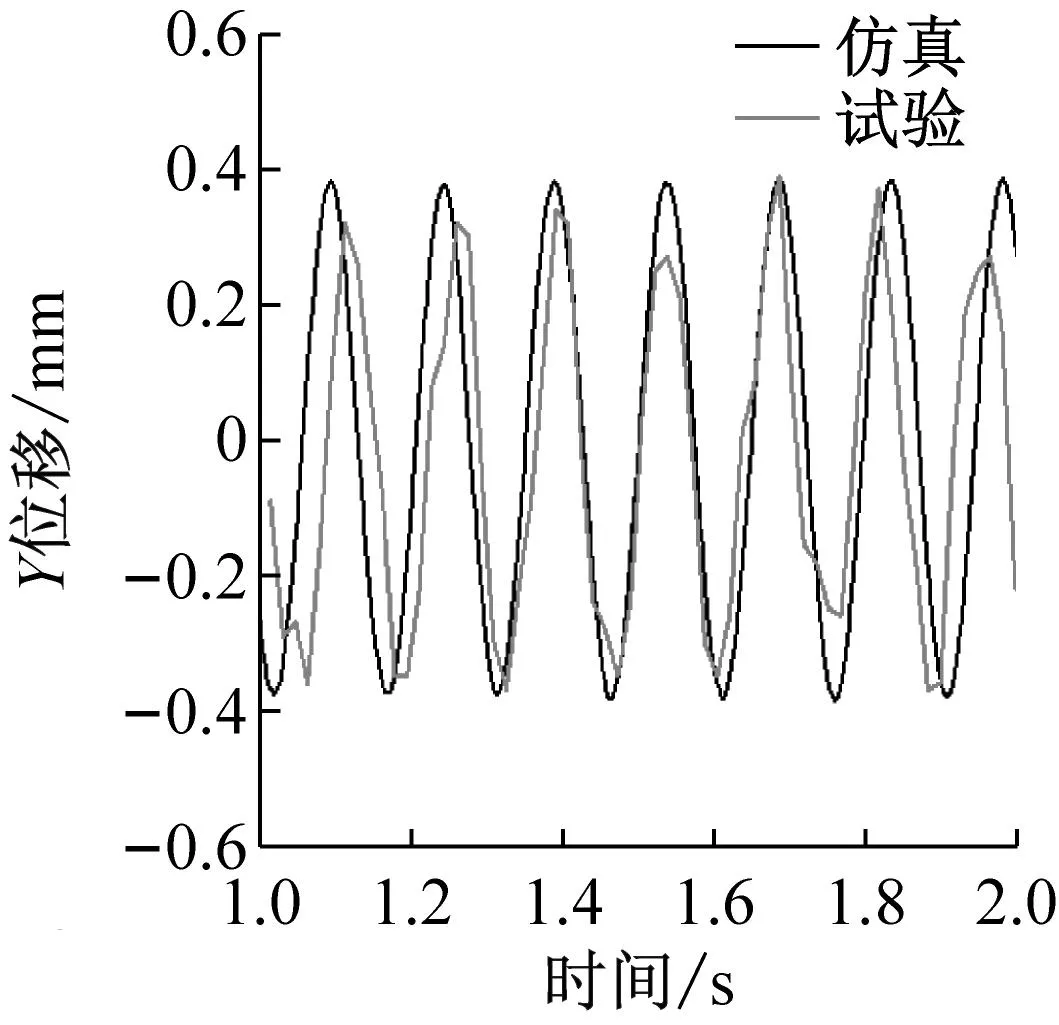
(c) Y方向位移响应图19 球兜孔保持架质心运动Fig.19 Spherical pocket cage motion

此外,试验结果还表明方形和圆形兜孔保持架的质心轨迹直径等于保持架引导间隙,而球兜孔保持架的质心轨迹直径等于兜孔间隙,从而试验证明了圆形和方形兜孔保持架由套圈引导,而球兜孔保持架由球引导;并且试验结果还表明方形、圆形和球形兜孔保持架的轴向摆动范围逐渐减小,这些与仿真分析结论均是一致的。

4 结 论

本文建立了方形、圆形和球形兜孔保持架的高速角接触球轴承动力学数值仿真模型,并通过试验验证了三种兜孔形状保持架动力学模型的正确性,在此基础上,详细探讨了保持架兜孔形状及兜孔间隙对保持架动力学特性的影响,并得出如下结论:

(1) 试验和仿真结果均表明方形和圆形兜孔保持架由套圈引导,而球兜孔保持架由球引导;方形、圆形和球形保持架的轴向摆动范围依次减小。

(2) 随着兜孔间隙的增大,三种兜孔形状的保持架稳定性均逐渐降低,保持架轴向摆动范围逐渐增大,且球兜孔保持架稳定性远高于方兜孔和圆兜孔保持架稳定性,轴向摆动范围也低于方兜孔和圆兜孔保持架;间隙比小于1时,方兜孔保持架稳定性优于圆兜孔,而间隙比大于1时则劣于圆兜孔。

(3) 保持架的运动与钢球和套圈之间的受力相关。保持架的径向涡动半径主要受保持架和套圈之间的作用力影响,保持架的轴向摆动以及周向速度主要受保持架兜孔与球之间的作用力影响。球兜孔保持架与球和套圈之间的作用非常小,因此运动很稳定。

(4) 方形和圆形兜孔保持架的磨损主要发生在引导面上,而球兜孔保持架的磨损主要发生在兜孔面上。随着兜孔间隙的增大,三种兜孔保持架的磨损率均逐渐降低,且球兜孔保持架的磨损率远高于另两种保持架。