多胞薄壁铝合金方管载荷特性与多目标优化研究

李耀宙，张冰冰，薛仲卿，范志强

多胞薄壁铝合金方管载荷特性与多目标优化研究

李耀宙1，张冰冰1，薛仲卿1，范志强2*

（1.太原工业学院，太原 030008；2.中北大学，太原 030051）

通过引入边长系数，得到构型不同的W型和C型多胞薄壁方管结构，改善多胞薄壁方管的吸能效率。本文利用实验和数值方法对2种类型方管进行研究，材料选用6060T4铝合金，深入分析边长系数和壁厚对结构的载荷特性、能量吸收及变形模式的影响。然后采用非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ）求解，针对结构的峰值载荷（c）和比吸能（a）进行多目标优化。数值仿真所得载荷曲线与实验结果一致，折叠波数均为7个，边长系数对2类结构的载荷和变形有显著影响。本文所得结果为改善多胞薄壁方管结构的缓冲吸能及冲击防护提供了数据支持。

多胞薄壁方管；边长系数；响应面模型；非支配排序遗传算法（NSGA-Ⅱ）；多目标优化

薄壁方管广泛应用于冲击防护领域，该类几何结构在其受到冲击载荷作用时，折叠变形较为规则，具有较高的能量吸收效率，一直受到很多学者的关注。基于几何拓扑学和仿生学，很多学者提出不同类型的几何结构，通过理论分析，数值模拟和实验等方法对薄壁方管的载荷特性进行分析。关于薄壁方管的研究主要包括Chen等[1]较早提出单层管多胞化，相同质量的双胞薄壁管和三胞薄壁管能显著提高结构的载荷，并基于超折叠单元建立3种薄壁管理论压缩载荷预测表达式。基于Chen和Wierzbicki的研究结果，张雄[2]将多胞方管截面拆分为角形部分、十字形部分和T形部分，通过对3个部分分别计算，提出了新的多胞管的平均载荷公式，推导的多胞方管理论未区分多胞方管结构的非均匀分布，显然是不完备的，因此Nia等[3]通过引入尺寸系数修正了多胞薄壁方管的平均载荷公式，通过试验和仿真证明此类薄壁管比单管结构的比能量吸收提高了227%。Xie等[4]对不同类型多胞方管进行研究，根据数值方法针对峰值载荷和比吸能进行优化。根据以上研究，可以通过改变方管结构的拓扑构型研究多胞方管力学特性。Li等[5]和Fang等[6]针对等质量单胞、四胞、五胞管进行力学分析，紧接着对五胞薄壁管的峰值载荷和比吸能进行优化得到最佳结构尺寸。Xu等[7]基于仿真力学提出2种多级多胞方管，并对结构的折叠模式进行分析，最后针对薄壁方管进行尺寸优化。Wang等[8-9]针对胞数不同胞数多胞方管进行理论分析，结果表明半波长影响平均压溃载荷的大小，随着胞数的增加，能量吸收逐渐提高。Zou等[10]研究8种多胞方管在轴向和斜向载荷作用下的载荷特性，发现T5-1管结构具有最佳的耐撞性能，最后将直管改为锥形管进行了结构改进设计。以上学者主要是在角元处增加角元来提高多胞方管的力学特性。Qin等[11]基于竹子的梯度多孔结构提出多级正四边形薄壁结构，通过数值分析，当宽厚比达到600时4th类结构的变形出现局部屈曲模式，该折叠模式不利于能量吸收。Ha等[12]基于仿生结构提出多级多胞方管，结果表明三阶BHMS的a比普通BHMS的高178.4%。基于有限元分析，提出3种折叠模式，分别为渐进折叠模式，混合折叠模式和欧拉屈曲模式。因此，多胞方管多极化可以改善多胞方管的能量吸收效率。

综上所述，以上学者利用实验和有限元方法通过增加角元或多极化对多胞薄壁方管的载荷特性和a进行研究。本文在以上研究方法基础上，针对截面长度相等的多胞薄壁方管进行研究，提出边长系数，利用数值方法针对不同边长系数的W型和C型多胞薄壁方管的载荷特性、能量吸收和变形模式进行分析，结合多项式响应面构建代理模型对多胞薄壁方管的和进行优化设计，为该类结构在能量吸收和力学防护领域提供数据支持。

1 多胞铝合金方管结构模型

单层薄壁方管是最简单的薄壁管，很多学者针对其折叠进行分析，但是该结构载荷和吸能效率较低。本文提出不同结构多胞薄壁铝合金方管，如图1所示，分为W型结构和C型结构，结构的边长系数=/，分别为0.25，0.50，0.75和1.0，分别命名为W-0.25、W-0.50、W-0.75、W-1.0、C-0.25、C-0.50、C-0.75和C-1.0。当W-0/C-0的壁厚分别为0.5、1.0、1.5、2.0、2.5和3.0 mm时，对其等质量多胞化，其壁厚分别为0.25、0.50、0.75、1.0、1.25和1.50 mm，所有方管长度均为150 mm，边长为60 mm，其质量分别为48.6、97.2、145.8、194.4、243和291.6 g。

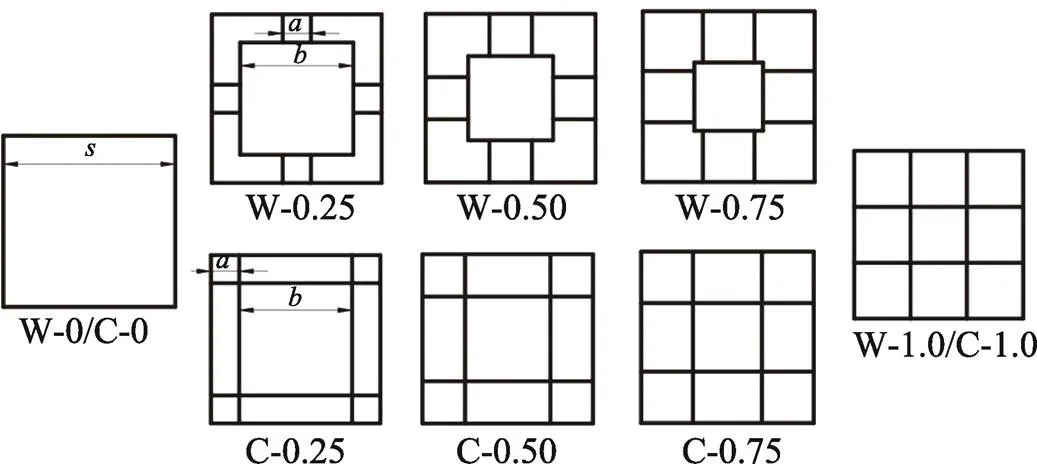
图1 W型和C型多胞方管

2 载荷特性分析

2.1 实验与数值模型验证

对6060T4铝合金进行准静态拉伸实验，实验所用拉伸试样采用火花线切割方法（WEDM）获得，为消除试样内部应力对其进行退火热处理。采用万能试验机进行拉伸压缩实验，其型号为WDW-E200（≤200kN），速度范围为0.1～500 mm/min，如图2a所示。将哑铃状试样放在夹具中间夹紧，拉伸速度为1 mm/min，直到试样被拉断，得到6060T4铝合金的工程应力-应变曲线，如图2b所示。材料的弹性模量=75 GPa，屈服应力y=86.7 MPa，极限应力u=130.7 MPa，密度s=2 700 kg/m3，泊松比=0.3，该材质的应变率效应不明显[4, 12]。本文采用WEDM对原料进行切割得到=1的多胞方管结构，如图2c所示，对其进行退火处理。将多胞薄壁方管放在万能试验机平台的中心位置，以5 mm/min的速度匀速向下压缩，薄壁管开始变形，数据采集系统记录压缩过程得到的载荷和位移，其变形过程如图2d所示。

利用有限元分析软件LS-DYNA模拟轴向压缩作用下多胞方管结构载荷特性，数值模型如图3a所示。上下端面刚性板，材料模型为MAT-1，中间为薄壁方管，材料模型为MAT-123[13]。考虑到仿真计算时间，顶端刚性板沿轴向以5 m/s的恒定速度压缩多胞薄壁方管，底端刚性板采用全约束进行固定[4, 7, 12]。为了准确地模拟薄壁管的大变形，薄壁采用Beltschko-Tsay四边形壳单元，单元厚度方向采用五点积分。薄壁管壁采用自动单面接触算法（Automatic Single Surface）来模拟自身变形产生的接触，薄壁管与刚性板之间采用自动点-面接触算法（Automatic Node to Surface），数值模型中的静动摩擦因数分别取0.3和0.2[14]。考虑到计算时间和收敛关系，本文对其进行网格敏感性分析，如图3b所示，最终本文采用0.5 mm× 0.5 mm的网格尺寸。同时为了验证本文有限元计算的合理性，对有限元算法进行验证，如图3c所示，总折叠波数均为7个，其平均压溃力m的误差为1.82%，可见本文采用的有限元算法是合理可行的。

图2 实验装置、材料应力应变曲线及多胞方管变形过程

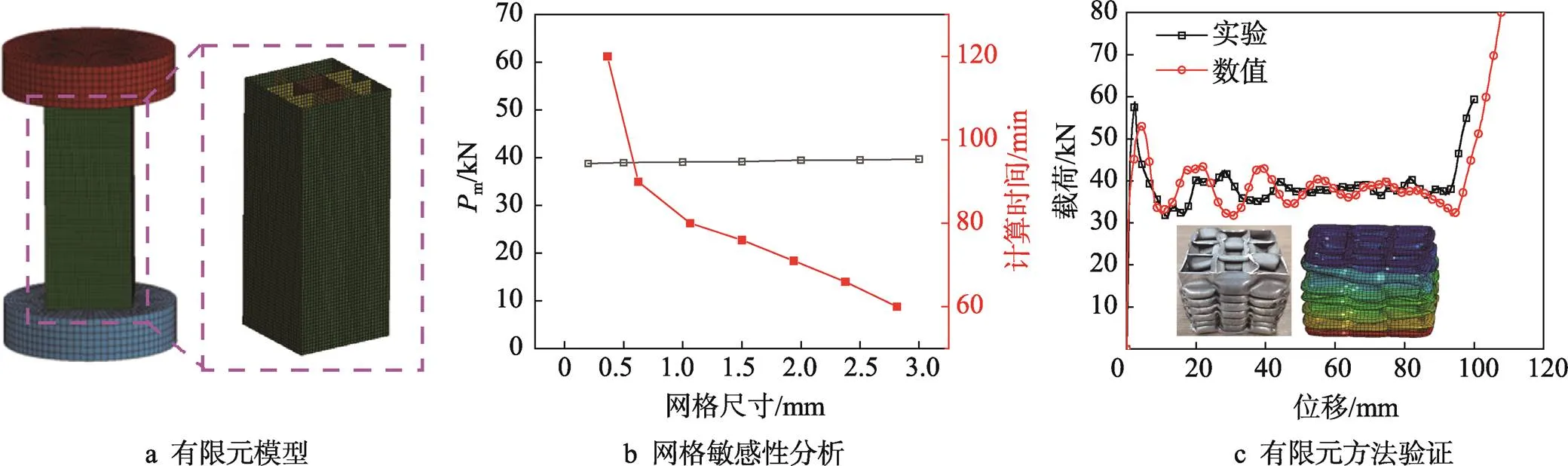
图3 数值模型验证与网格敏感性分析

2.2 评价指标

为了有效评估薄壁结构的力学性能，本文引入评估指标，包括总能量吸收（a）、平均压溃力（m）、比吸能（a）。其中a是塑性变形过程中吸收的总能量，其数学表达式见式（1）[15]。

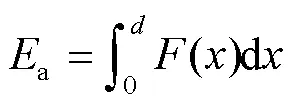
m为吸收的总能量除以变形长度，其数学表达为：

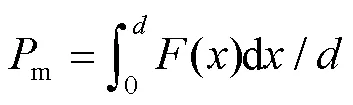
a是总能量吸收除以薄壁结构的质量，其数学表达见式（3）。

a=a/(3)

2.3 载荷特性与变形模式

通过对W型和C型多胞方管进行计算，得到=0.25、0.50、0.75和1.0的结构的载荷位移曲线，如图4a～f所示，厚度分别为0.25、0.50、0.75、1.0、1.2和1.50 mm的W型结构载荷位移曲线。图4g～p为C型结构的厚度分别为0.25、0.50、0.75、1.0、1.25和1.50 mm的载荷位移曲线。W型结构6种厚度的平台段载荷变化范围分别为3.72～5.33 kN、11.75～15.37 kN、19.59～30.16 kN、33.68～49.05 kN、47.61～72.22 kN和48.92～91.08 kN，其载荷差值分别为1.61、3.62、10.57、15.37、24.61和42.16 kN。C型结构的6种厚度的平台段载荷变化范围分别为3.63～4.78 kN、10.53～13.90 kN、19.66～26.67 kN、30.31～42.67 kN、39.22～61.66 kN和53.48～83.11 kN，其载荷差值分别为1.15、3.37、7.01、12.36、22.44和29.63 kN。由此可知，随着方管壁厚增加，平台段载荷变化范围增大，意味着当方管壁厚为0.25～0.50 mm时，边长系数对平台段载荷影响较小，随着方管壁厚增加，边长系数对平台段载荷影响较大。

W结构和C结构的m如表1所示。本文以压缩方管长度的70%为有效位移，当方管壁厚较小时，W型系列结构和C型系列结构的载荷相差不大，随着方管壁厚增加，2种结构的载荷逐渐有差别。对于不同壁厚的W结构，当=0.50时结构的m值最高；对于不同壁厚的C结构，当=1.0时结构的m值最高。总之，对于相同质量的方管结构，其m值有差别，这与边长系数和方管壁厚有关系，因此本文进一步分析边长系数和方管壁厚对2种结构的折叠模式的影响。

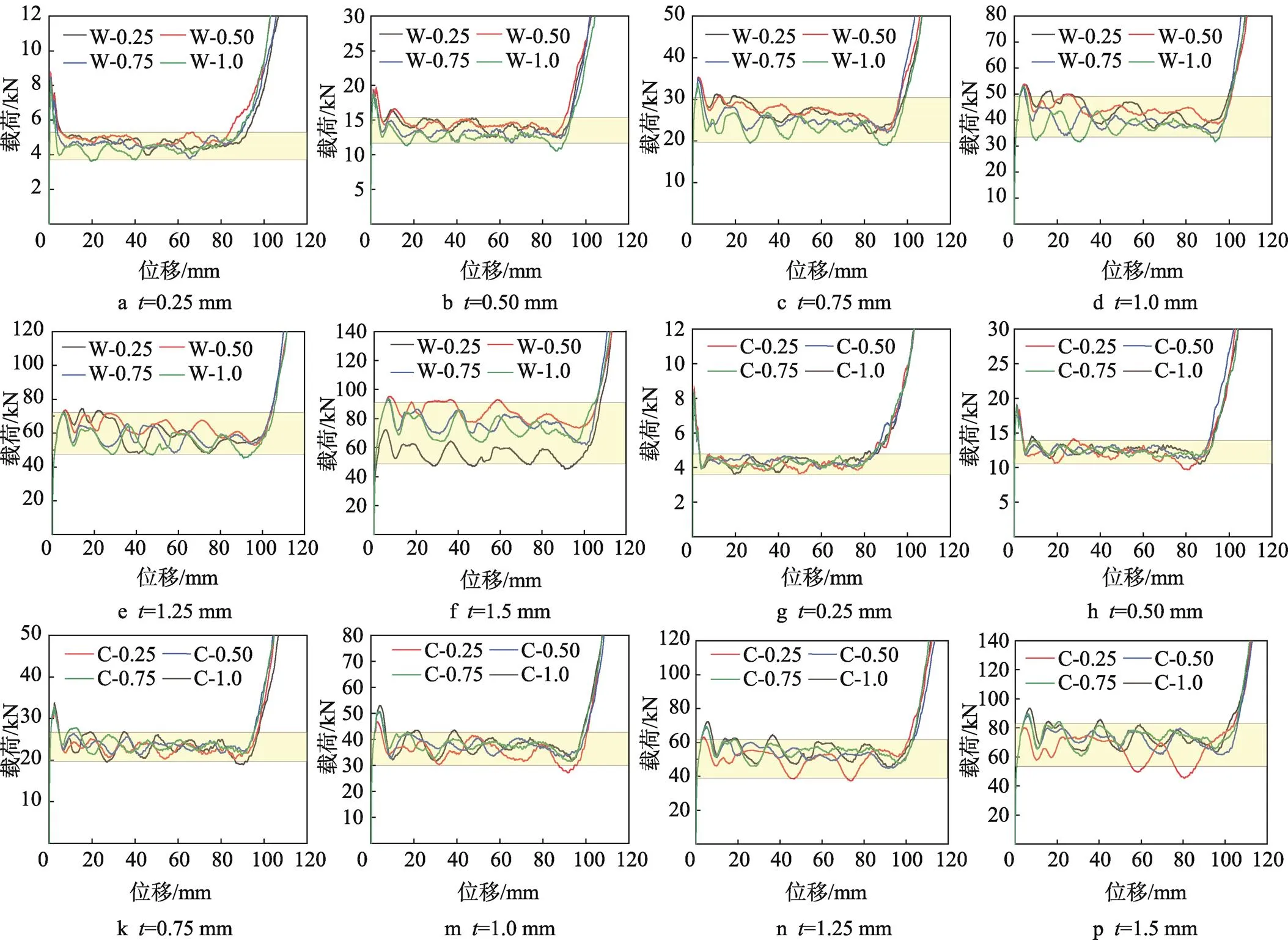
图4 W型和C型多胞方管载荷位移曲线

表1 W型和C型方管的m

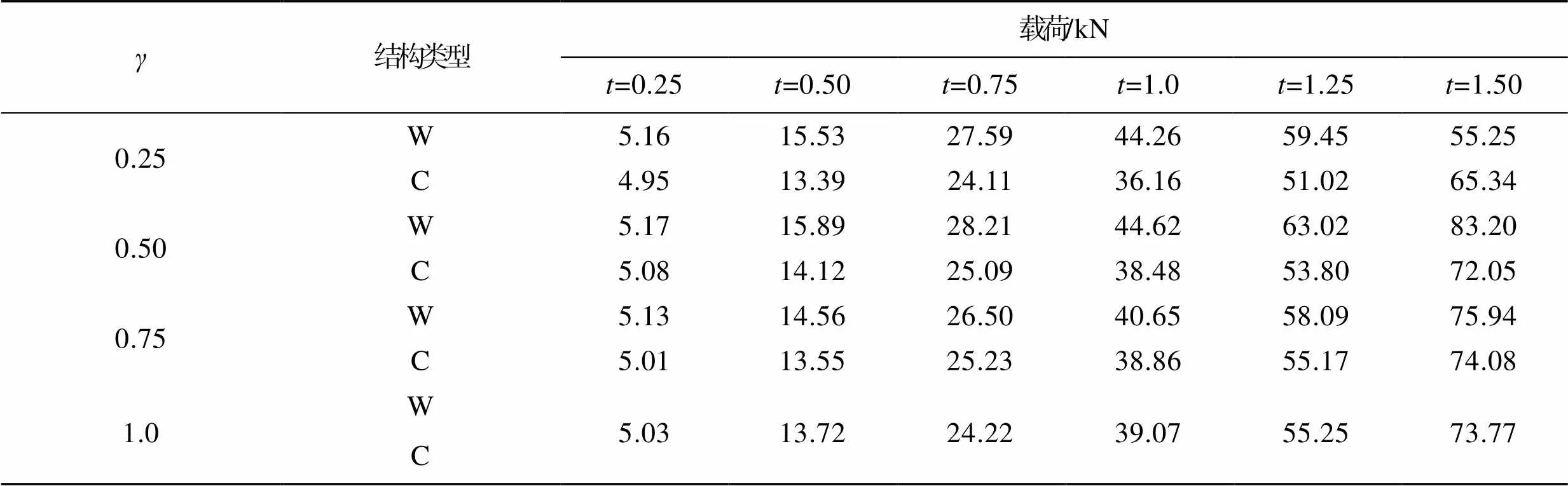
Tab.1 Pm of W-type and C-type square tubes

W型多胞方管折叠变形如图5所示。对于W-0.25，=0.25 mm和0.50 mm的结构，其边长与壁厚比值较大，方管在被压缩时能够有序的折叠，随着方管壁厚增加，与比值减小，方管在被压缩时出现局部屈曲变形；当=1.5 mm时，方管变形模式为整体屈曲，其a值为19.89 J/g，影响结构的能量吸收。相比其他W型方管，不同壁厚的W-0.50结构折叠相对规则，因此结构的能量吸收效率最高。W-0.75结构的a值低于W-0.50的，这是由于肋板靠近4个角元，导致内管的4个角元折叠不规则。因此为了提高结构的能量吸收，在对多胞结构设计时，尽量避免较小尺寸的角元。W-1.0整体上折叠相对规则，这样有利于提高结构的吸能，然而其a仍然低于W-0.25、W-0.50和W-0.75的a值。这是由于W-1.0的薄膜能比以上三者的低一些，本文通过理论分析进一步解释。

图6为C型方管结构变形模式，未出现整体屈曲变形，总体上随着方管壁厚的增加a值逐渐增加。对C-0.25结构，随着壁厚增加，结构的4个角处折叠变形改变，当=0.25 mm和0.50 mm时，方管4个角处能够有序折叠；当=1.5 mm时，4个角折叠变得不规则。随着增加，其余C型结构能够有序折叠。通过对比不同壁厚C型方管，当壁厚为0.25 mm时，4种不同方管被压缩时都能够有序折叠，因此结构的a相差不大；当壁厚为1.5 mm时，=0.25的结构由于4个角处存在尺寸较小的角元，该角元结构会影响多胞方管的稳定折叠变形，从而影响结构的能量吸收；=1.0时的a值最大，此时方管能够有规则的折叠，从而提高结构的能量吸收。

图5 W型多胞方管折叠变形与Sa

图6 C型薄壁方管折叠变形与Sa

2.4 理论分析

根据简化的超折叠单元理论，薄壁方管吸收的能量包括弯曲变形能b和薄膜变形能m两部分。在单个折叠单元完全压溃过程中，轴向压缩所做的外部功被折叠单元的弯曲和膜的变形所耗散[2]：

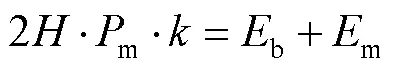
式中：m为平均压溃力；为折叠半波长；为有效压缩系数。b可以表达为：

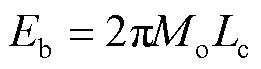
式中：o为折叠单元弯矩；c为截面长度。文中W型和C型多胞薄壁方管的c相同，因此W型和C型结构的b相同。

角形结构的薄膜变形能m, c=402，T形结构的薄膜变形能m, T=802/，十字形结构的薄膜变形能m, o=1602/，因此总的薄膜变形能表示为：

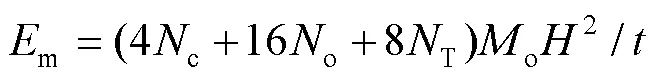
式中：c、T和o分别为角形、T形和十字形结构的数量；为多胞薄壁方管壁厚。

将式（5）和式（6）代入式（4），则W型多胞薄壁方管的m表达为：

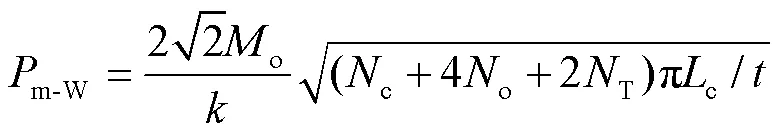
当=0.25、0.50和0.75时，c、T和o分别为8、16和0。对于壁厚为1.0 mm的多胞方管，m-W为41.94 kN，而表1中=0.50的m值最高，表明系数对多胞方管的载荷有显著影响，需要找出多胞薄壁方管的最佳。当=1.0时，c、T和o分别为4、8和4，W型结构的实验、数值和理论的m-W如表2所示，最大误差为2.17%，表明式（7）是准确的。

表2 实验、数值和理论m对比

Tab.2 Comparison of experimental, numerical, and theoretical Pm

对于C型结构，根据文献针对不均衡多胞方管引入角元尺寸系数，m可以表达为[3]：

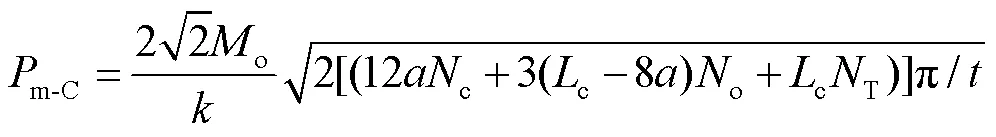
其中，c、T和o分别为4、8和4，代入式（8）得：

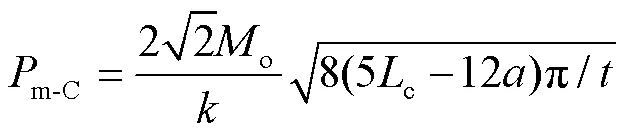
由式（9）可知，m-C随着的增加而降低，这与表1的变化规律是不符合的。这是由于方管壁厚较小时，子胞长度对载荷影响较小。随着方管壁厚增加，子胞长度对载荷影响较大，为使C型结构吸收能量最高，需针对C型结构进行优化，找到合适的值。

3 优化分析

多目标优化在求解耐撞性优化问题时，由于各目标通常是相互冲突的，因此所得到的解非单一解而是一系列解，即Pareto前沿解集，多目标优化的任务就是找到近似Pareto前沿的尽可能多的非劣解以供决策。第二代非劣排序遗传算法（NSGA-Ⅱ）因其相对较短的收敛耗时与良好的Pareto解集分布而被广泛应用于解决多目标优化问题，所以文中选取NSGA-Ⅱ优化算法，其参数设置如表3所示[16-17]。

表3 NSGA-Ⅱ优化算法参数设置

Tab.3 Parameters definitions for NSGA-Ⅱ optimization algorithm

3.1 样本点选取

本文通过多目标优化的方式来寻找最优目标，本文选取峰值载荷（c）和比吸能a作为目标函数，和作为自变量，其中变量范围如式（10）所示.

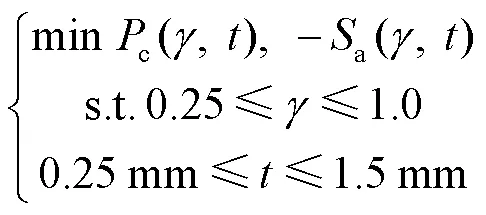
3.2 多项式响应面

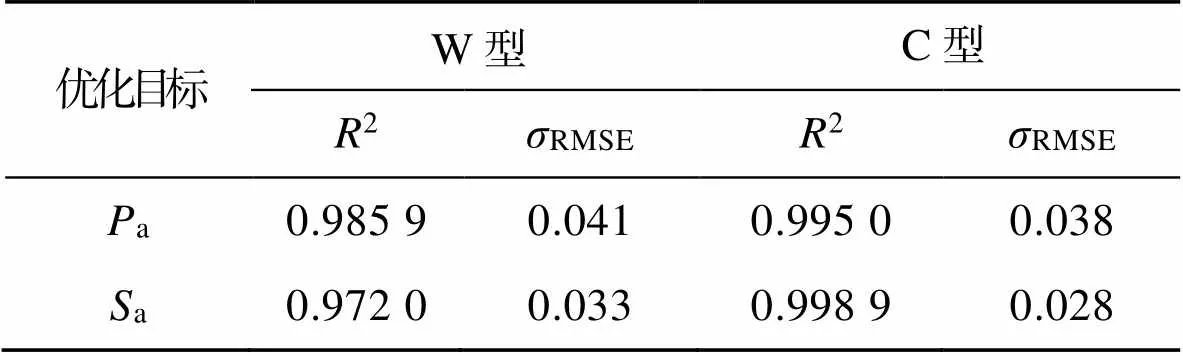
本文采用多项式响应面模型（RSM）作为代理模型，引入平方值误差（2）和均方根误差（RMSE）是用来评估这些代理模型的准确性。2是在0和1之间的值，认为超过0.9在可接受的范围内。同时RMSE越小越好，一般小于0.2认为可接受。2的计算见式（11）。

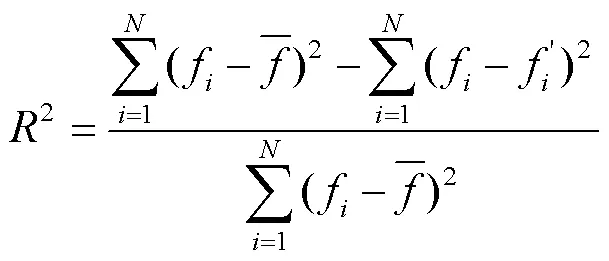
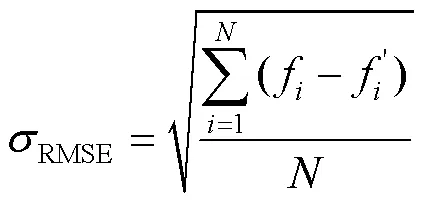
根据表4的响应面误差分析，本文采用多项式响应面代理模型能够很好拟合目标值函数，W型和C型结构响应面如图7a～d所示。边长系数对2种结构的a有显著影响，对c影响不大。方管壁厚对2种结构的c和a都有显著影响。

表4 响应面误差分析

Tab.4 Response surface error analysis

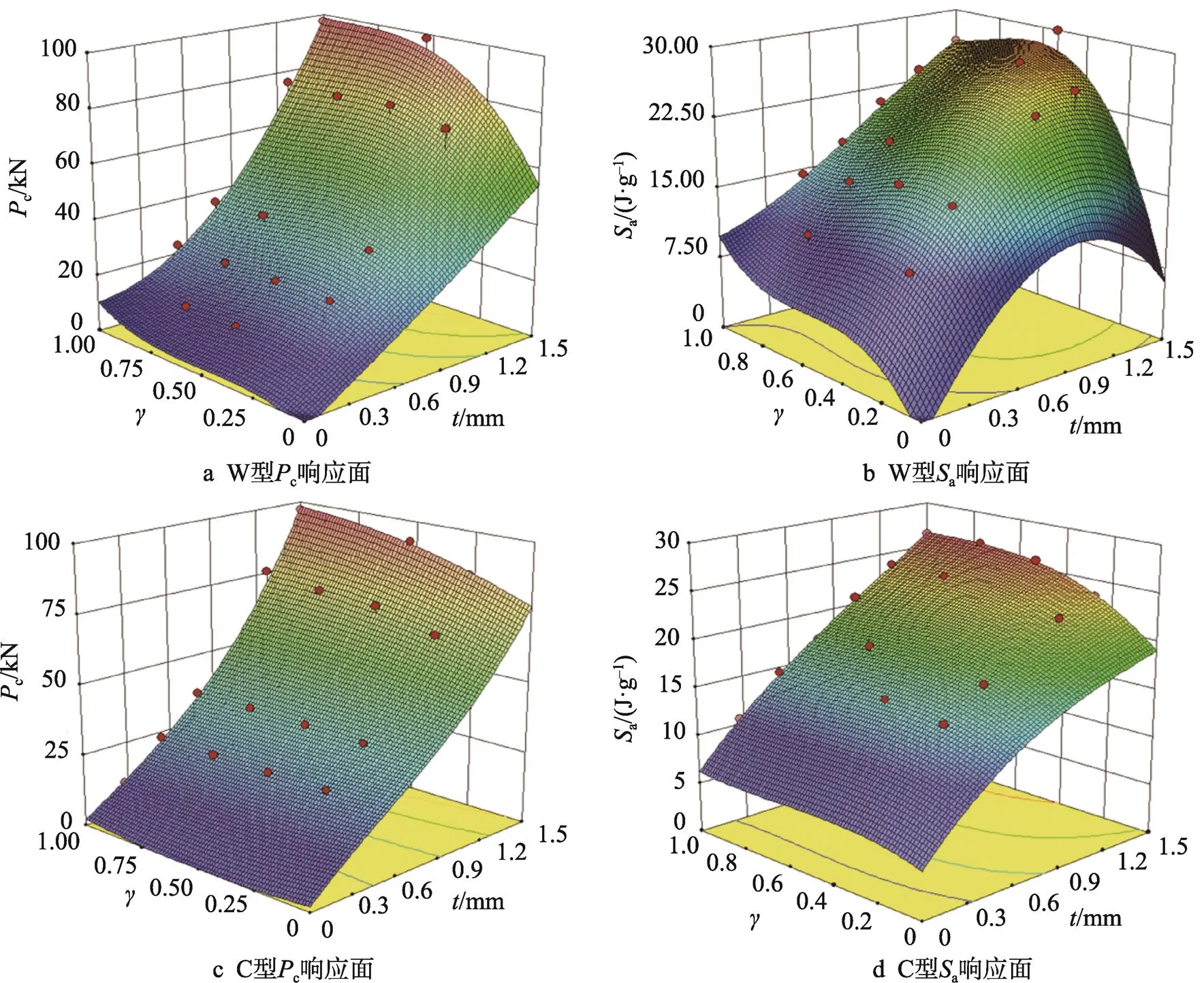
图7 W型和C型方管响应面结果

3.3 多目标优化结果

基于3.2节中所构建的目标函数与设计变量的多项式响应面代理模型，采用NSGA-Ⅱ算法进行寻优计算，得到了多胞方管耐撞性优化问题的Pareto前沿解集，如图8所示，2种结构随着a的增加c会提高。在给定c≤60 kN的情况下，其a为25.85 J/g和22.37 J/g，此时2类方管对应的最优设计变量如表5所示。本文利用有限元方法进行验证，其误差分别为2.10%和0.31%，均在合理范围之内，表明基于多项式响应面构建的多胞方管代理模型是准确可行的。

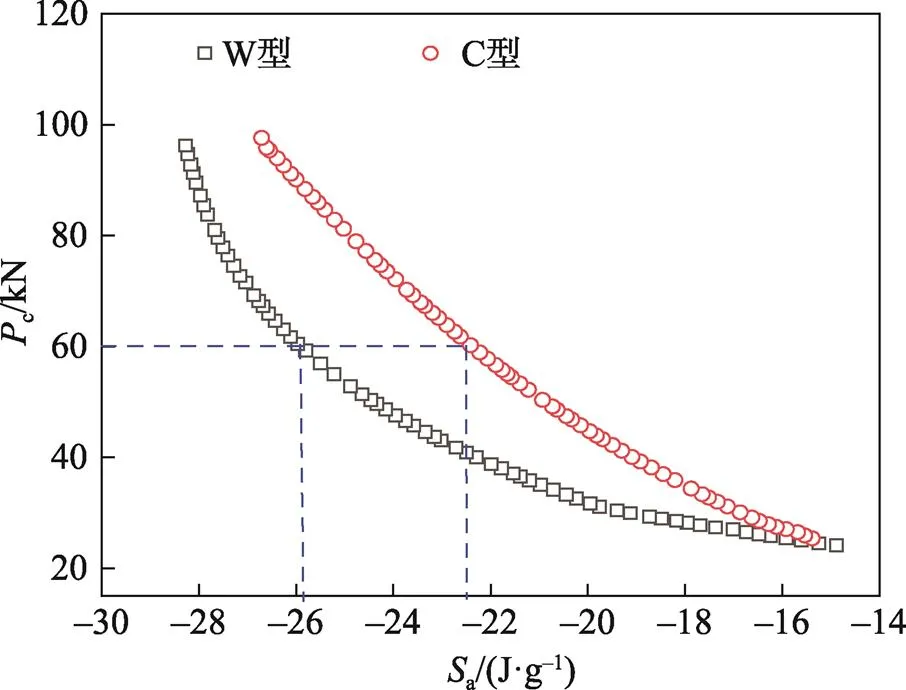
图8 多目标优化的Pareto前沿解集

表5 优化结果与数值验证

Tab.5 Optimization results and numerical verification

4 结语

本文将边长系数引入多胞薄壁方管，通过静态压缩实验、数值模拟和理论方法研究其载荷特性、变形模式和能量吸收特性，并采用NSGA-Ⅱ算法进行计算，得到多胞薄壁方管结构优化问题的Pareto前沿解集，提高该类结构的能量吸收和冲击防护能力，研究结果如下：

1）当方管壁厚为0.25～0.50 mm时，边长系数对平台段载荷影响较小。随着方管壁厚增加，边长系数对平台段载荷影响增加。

2）W型结构中，不同壁厚的W-0.50结构折叠较为规则，其m值最高，有利于多胞方管的能量吸收；C型结构中，C-1.0的a最大，因此避免小尺寸角元薄壁管设计。

3）通过构建响应面，采用NSGA-Ⅱ算法对边长系数和壁厚进行优化。在给定c≤60 kN的情况下，W型和C型的a分别为25.85 J/g和22.37 J/g，并利用有限元方法进行验证，其误差分别为2.10%和0.31%，均在合理范围之内。

[1] CHEN W, WIERZBICKI T. Relative Merits of Single-Cell, Multi-Cell and Foam-Filled Thin-Walled Structures in Energy Absorption[J]. Thin-Walled Structures, 2001, 39: 287-306.

[2] 张雄. 轻质薄壁结构耐撞性分析与设计优化[D]. 大连: 大连理工大学, 2007: 82-85.

ZHANG X. Crashworthiness Analysis and Design Optimization of Lightweight Thin-Walled Structures[D]. Dalian: Dalian University of Technology, 2007: 82-85.

[3] NIA A A, PARSAPOUR M. An Investigation on The Energy Absorption Characteristics of Multi-Cell Square Tubes[J]. Thin-Walled Structures, 2013, 68: 26-34.

[4] XIE S, YANG W, WANG N. Crashworthiness Analysis of Multi-Cell Square Tubes Under Axial Loads[J]. International Journal of Mechanical Sciences, 2017, 121: 106-118.

[5] LI S. WU G Z. On Design of Multi-Cell Thin-Wall Structures for Crashworthiness[J]. International Journal of Impact Engineering, 2016, 88: 102-117.

[6] FANG J, GAO Y, SUN G. On Design of Multi-Cell Tubes Under Axial and Oblique Impact Loads[J]. Thin-Walled Structures, 2015, 95: 115-126.

[7] XU S, LI W, LI L. Crashworthiness Design and Multi-Objective Optimization for Bio-Inspired Hierarchical Thin-Walled Structures[J]. Computer Modeling in Engineering & Sciences, 2021, 131: 2-21.

[8] WANG Z, LIU J, YAO S. On Folding Mechanics of Multi-Cell Thin-Walled Square Tubes[J]. Composites Part B, 2018, 132: 17-27.

[9] WANG Z, LIA Z, SHI C. Mechanical Performance of Vertex-Based Hierarchical Vs Square Thin-Walled Multi-Cell Structure[J]. Thin-Walled Structures, 2019, 134: 102-110.

[10] ZOU X, GAO G, DONG H. Crashworthiness Analysis and Structural Optimisation of Multi-Cell Square Tubes Under Axial and Oblique Loads[J]. International Journal of Crashworthiness, 2011, 16: 1-14.

[11] QIN S, DENG X, LIU X. Crashworthiness Analysis of Bioinspired Hierarchical Gradient Multicell Tubes Under Axial Impact[J]. Thin-Walled Structures, 2022, 179: 109591.

[12] HA N S, PHAM T M, HAO H. Energy Absorption Characteristics of Bio-Inspired Hierarchical Multi-Cell Square Tubes Under Axial Crushing[J]. International Journal of Mechanical Sciences, 2021, 201: 106464.

[13] LI Y, FAN Z, HU S, et al. Mechanical Performance of Multi-Cell Thin-Walled Tubes Under Static and Dynamic Axial Loading[J]. International Journal of Crashworthiness, 2023, 29: 218378.

[14] FAN Z, TAN X, HU J, et al. A Comparative Study on Dynamic Compression Response of Multi-Cell Thin-Walled Structures with Filling Foams and Connecting Ribs[J]. International Journal of Crashworthiness, 2023, 28: 22306.

[15] LI Y, FAN Z, HU S. Dynamic Enhancement Mechanism of Energy Absorption of Multi-Cell Thin-Walled Tube[J]. Thin-Walled Structures, 2022, 178: 109449.

[16] 杨霞, 王先正, 赵春江, 等. 基于Kriging模型的调心滚子轴承优化设计[J]. 机械设计与研究, 2021, 37(6): 101-106.

YANG X, WANG X Z, ZHAO C J, et al. Kriging Model Based Optimization of Spherical Roller Bearing[J]. Machine Design & Research, 2021, 37(6): 101-106.

[17] 于文吉, 石昌玉, 魏明, 等. 基于响应面法与 NSGA-II的重组竹翻转夹爪优化设计[J]. 包装工程, 2023, 44(19): 187-196.

YU W J, SHI C Y, WEI M, et al. Optimization Design of Recombinant Bamboo Flipping Claw Based on Response Surface Methodology and NSGA-II [J]. Packaging Engineering, 2023, 44 (19): 187-196.

Mechanical Performance and Multi-objective Optimization of Multi-cell Thin-walled Aluminum Alloy Square Tubes

LI Yaozhou1, ZHANG Bingbing1,XUE Zhongqing1,FAN Zhiqiang2

(1. Taiyuan Institute of Technology, Taiyuan 030008, China; 2. Central North University, Taiyuan 030051, China)

The work aims to obtain W-type and C-type multi-cell thin-walled square tubes with different configurations through the introduction of side coefficientto improve the energy absorption efficiency of multi-cell thin-walled square tubes. Experimental and numerical methods were adopted to study two types of square tubes made of 6060T4 aluminum alloy. The effects of side coefficientand wall thicknesson the mechanical performance, energy absorption and deformation mode of the structure were analyzed in depth. Then, the Non-dominated Sorting Genetic Algorithm (NSGA-Ⅱ) was used to analyze the thin-walled square tubes. Multi-objective optimization was carried out for the peak load (c) and specific energy absorption (a). The load curves obtained by numerical simulation were consistent with the experimental results. There were 7 folded waves. The side coefficienthad a significant influence on the load and deformation of class 2 structures. The results obtained in this work provide data support for improving the buffering energy absorption and impact protection of thin-walled square tube structures.

multi-cell thin-walled square tube; coefficient of side; RSM; NSGA-Ⅱ; multi-objective optimization

TB482.2

A

1001-3563(2024)07-0246-08

10.19554/j.cnki.1001-3563.2024.07.030

2024-01-08

国家自然科学基金（12072326）；山西省科技厅基础研究计划自由探索类青年项目（202203021222281）；山西省高等学校科技创新项目（2023L341）；太原工业学院引进人才科研资助项目（2023KJ043）

通信作者