侧向局部爆炸下钢质方管损伤特性数值研究*

李鹏鹏，高振儒，陈叶青，周兆鹏，黄骏逸

(1.陆军工程大学 野战工程学院，南京 210007；2.军事科学院 国防工程研究院，北京 100036)

爆炸恐怖袭击长期危害世界和平稳定，其主要方式是利用汽车炸弹、人体炸弹及邮件炸弹等方式实施接触爆炸和近距离爆炸，随着制导技术的快速发展，远程精确打击也现身爆炸恐怖袭击当中[1-3]。钢质管柱具有强度高和延展性好等特点，被广泛应用于厂房、桥梁等各种工程结构中，一旦遭受爆炸损伤，结构的承载能力势必会降低。特别是重要承重构件遭到破坏，可能引起整体结构的失稳，触发连续性倒塌，造成人员伤亡和重大经济损失[4-9]。所以钢质管柱抗爆能力的研究必须得到重视。

目前，国内外学者在工程防爆抗爆研究领域取得了一些阶段性科研成果，主要涉及三方面：爆炸与冲击波传播规律，单个构件或节点在爆炸中的破坏模式，及整体结构在爆炸荷载下的动力响应。主要的研究手段有：试验、数值模拟及基于单自由度(SDOF)结构体系假定的解析方法等。

Krishnappa等通过试验和有限元模拟的方法[10]，研究了垂直于弯曲弱轴施加爆炸荷载对宽翼缘柱的影响。Mazurkiewicz等提出了一种非常有效的爆炸荷载工字形柱承载能力评估的多阶段数值分析方法[11]。Maduliat等研究了横向冲击荷载作用下空心钢管的倒塌特性和能量吸收能力[12]。Nassr等采用试验、等效SDOF梁模型和有限元的多自由度(MDOF)模型分析等方法[13-15]，对13组典型宽翼缘钢立柱实施横向爆炸荷载和轴向加载进行了研究。Yan S等通过数值模拟的方法[16]，底端固定，区分顶端是可变约束几种不同情况，研究了爆炸荷载作用于轻型钢柱的动态响应和故障模式。Jama等利用数值模拟研究了薄壁方形钢梁在横向爆炸荷载作用下的破坏模式[17]，并指出了考虑应变率效应在研究钢结构抗爆特性中的重要性。

余洋等采用试验与数值模拟相结合方法[18]，研究了钢质方管在侧向局部爆炸荷载作用下的损伤破坏效应，分析了炸药比例距离 Z对结构迎爆面几何变形的影响，包括中心点挠度、凹陷变形区径向宽度及轴向长度等损伤变形特征参数，但对钢质方管损伤没有给出衡量标准，未能准确评估钢管损伤程度。

在本文在余洋等研究的基础上[18]，首先应用有限元软件LS-DYNA对建立的方管模型进行轴向承载能力测试，并与理论计算结果进行对比；而后区分不同爆距建立数值模型，数值分析与文献[18]中的试验结果进行比较；最后分析方管爆炸能量吸收能力和损伤指数变化规律，提出方管轴向承载能力损伤指数工程算法。

1 有限元模型

余洋等试验试件为Q235钢质方管[18]，壁厚3.5 mm，轴向长度100 cm，横截面尺寸10 cm×10 cm。爆源为密度1.61 g/cm3的裸装圆柱形压装160 g TNT药柱(φ48 mm×54 mm)，柱形炸药轴线正对方管迎爆面。参考试验[18]，建立模型，模型由空气、炸药、方管、上下刚性体5部分组成。采用CONSTRAINED_LAGRANGE_IN_SOLID流固耦合方式模拟空气、炸药与方管之间的相互作用，炸药与空气之间采用ALE_MULTI-MATERIAL_GROUP多物质耦合，无反射边界模拟无限空气域，方管与上下刚性体共节点连接，下刚性面板无平动与转动自由度，上刚性面板只有沿面板法向法向的自由度。方管两端添加刚性体，用以防止应力不均匀，出现应力集中，避免方管两端截面单元骤然变化而引起局部破坏。爆炸加载完毕，且方管停止振动后，施加轴向压缩荷载。为更直观展示模型各部分间的几何关系，有限元模型剖视图如图1所示。

图 1 有限元模型

1.1 材料参数

本文中，方管采用PLASTIC_KINEMATIC模型，该材料模型适合于模拟各向同性和运动硬化塑性，并且可以选择包括速率效应。使用Cowper和Symonds模型来计算应变率，该模型用DIF因子缩放屈服应力。

(1)

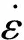
部分参数的取值如表1所示[16]。

表 1 钢材本构模型

假设空气为理想气体，采用9号MAT_NULL材料模型，状态方程用LINEAR_POLYNOMIAL表示，空气材料模型和状态方程部分参数的取值如表2所示[19]。

表 2 空气材料模型和状态方程参数

Table 2 Air MAT_NULL model and Air EOS_LINEAR_POLYNOMIAL state equation

TNT炸药采用8号*MAT_HIGH_EXPLOSIVE_BURN模型来模拟炸药在空气中的爆轰反应，状态方程用EOS_JWL表示，炸药材料模型和状态方程部分参数的取值如表3所示[11,19]。

1.2 方管力学性能

方管应变

ε=σ/E

(2)

极限受压状态下方管轴向收缩量

Δl=εH

(3)

方管应变速率

(4)

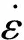
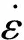
表 3 炸药材料模型和状态方程参数

1.3 数值模拟过程

第一步，以5.09×10-3s-1应变率轴向加载，直至方管失效。

第二步，重新加载，将横向爆炸荷载施加到方管上，爆炸荷载的作用时间可通过M A Sadovskyi公式求解[20,21]。

TNT炸药在无限空中爆炸，正压作用时间

(5)

(6)

式中：t+为正压作用时间；Z为比例距离；C为TNT当量；r为测点距炸药的距离。炸药质量C=0.16 kg。

比例距离Z=1.00 m·kg-1/3位置处的正压作用时间为0.7329 ms。

10 ms后，添加质量加权阻尼。使之50 ms后振动逐渐停止。Nemati A分析了不同阻尼值对承受冲击加载后方管的残留轴向承载能力的影响[22]，并证明添加阻尼对残余轴向承载能力没有影响。

第三步，接续第二步，以5.09×10-3s-1应变率轴向加载，直至方管失效，在此阶段施加到方管的最大荷载可认为爆炸荷载作用后方管的轴向残余承载力。

2 数值模拟

2.1 轴向承载能力数值模拟

2.1.1 方管模型

方管[18]，柱高H=100 cm，截面(mm)(100×100×3.5)，横截面面积S=13.51 cm2。方管LSDYNA三维有限元模型和横截面示意图如图2所示。

图 2 方管模型

2.1.2 轴向极限承载能力理论计算值

方管轴向极限承载能力

Fmax=Sσ

(7)

荷载增加速率

v=Fmax/t

(8)

1.2节方管力学性能，给出t为220 ms，故有Fmax=317.485 kN；v=1.4417 kN/ms。

式中:Fmax为方管轴向极限承载能力；v为方管横截面荷载增加速率。

方管轴向荷载、轴向位移同加载时间关系如图3所示。

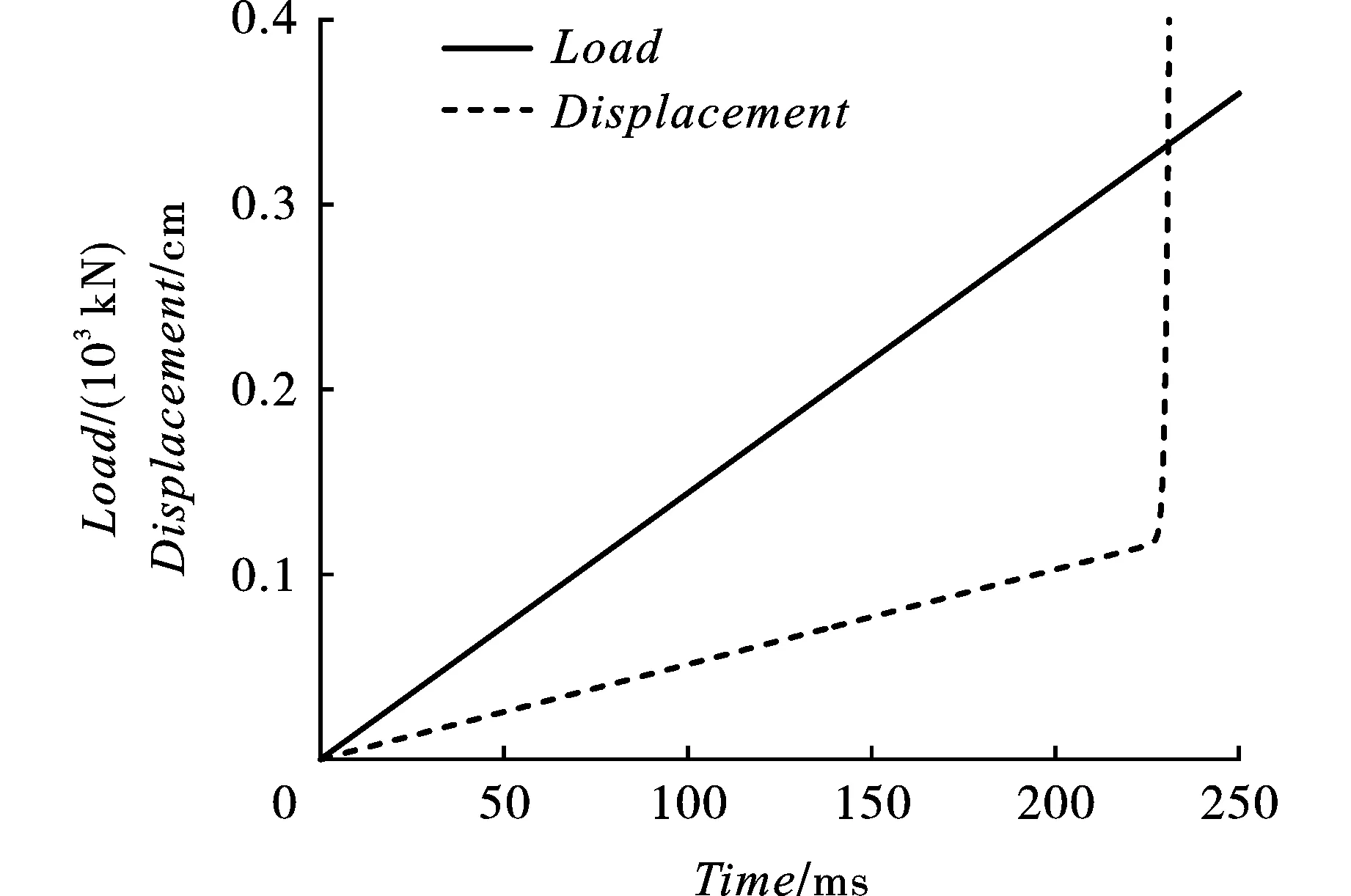
图 3 轴向荷载与轴向位移同加载时间关系

方管以v荷载增加速率加载，226.00 ms时刻，即轴向荷载325.8242 kN，方管轴向承载能力失效；方管轴向极限承载能力，理论计算值和数值模拟值相差2.63%。方管模型轴向失效承载能力数值模拟与理论计算值有一定误差，这跟LSDYNA中shell单元本身有很大关系，不影响本文的分析研究。

2.2 毁伤状况和试验对比

2.2.1 数值模拟结果

横截面毁伤状况如图4所示。

迎爆面中心点示意图如图5所示。

迎爆面中心点位移情况如图6所示。

图6展示了1.3节数值模拟过程中的第二步与第三步，达到了预期模拟效果。

2.2.2 数值模拟结果与试验结果对照

方管迎爆面中心点横向位移和爆距关系数值模拟结果与试验结果对照如图7所示。

图7表明，距离11.96cm、14.13cm、15.76cm、17.93cm、20.10cm，数值模拟获得的方管引爆面中心点位移与试验位移分别相差2.53%、7.72%、2.14%、10.11%、6.07%。考虑到爆破试验场地气压状况、温度湿度状况、试验本身设置误差及测量误差等因素，数值模拟结果和试验记录结果之间的微小差异可以被视为在可接受区间内，表明本文所建立的计算模型和选取的材料参数合理，数值计算结果可信。

图 4 中部横截面毁伤状况

2.3 残余轴向承载能力

不同爆距爆炸荷载下方管轴向承载能力持续时间如图8所示。

方管承受爆炸荷载后，短时间内，轴向方向均产生0.5 mm内的振幅，而后由于阻尼作用，轴向振动消失，方管轴向位移趋于稳定。50 ms后，方管开始承受逐渐增大的轴向压缩荷载。轴向位移在200～250 ms先后出现突跃，即轴向承载能力先后出现失效。同一方管，随爆距增加，方管轴向残余承载能力依次增加。

3 损伤分析

3.1 能量吸收分析

方管动能变化和内能吸收情况如图9所示。

方管动能在0.1 ms达到最大，而后迅速耗散，转化成方管的塑性变形，在约1 ms时刻，只剩下微弱的振动能量；方管的内能在约1 ms时刻达到最大值，而后出现轻微波动。以爆距13 cm为例，爆炸发生2.5 ms时刻，方管应变能密度和内能密度如图10所示。

图 5 迎爆面中心点示意图

图 6 迎爆面中心点横向位移

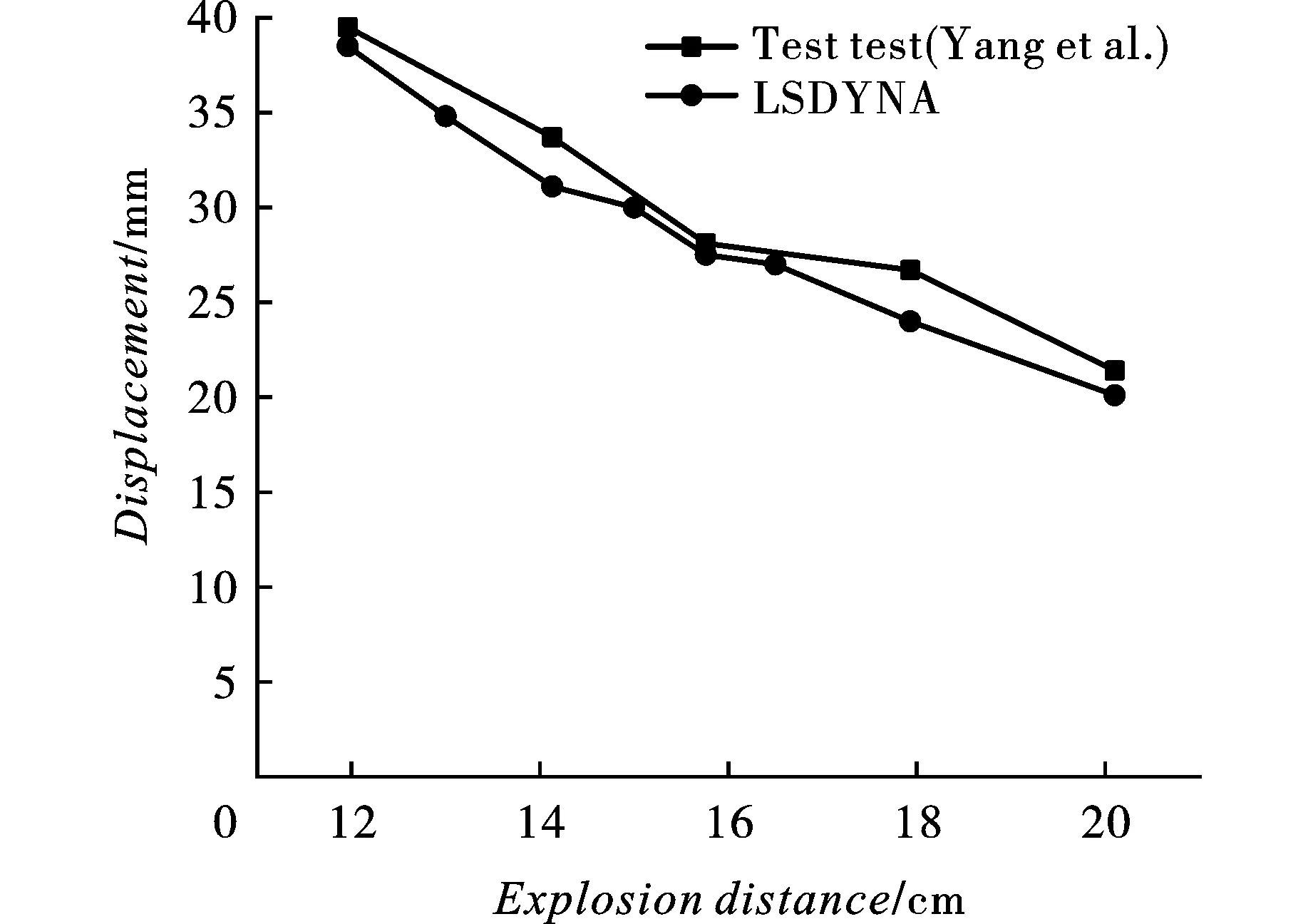
图 7 数值模拟结果与试验结果对比

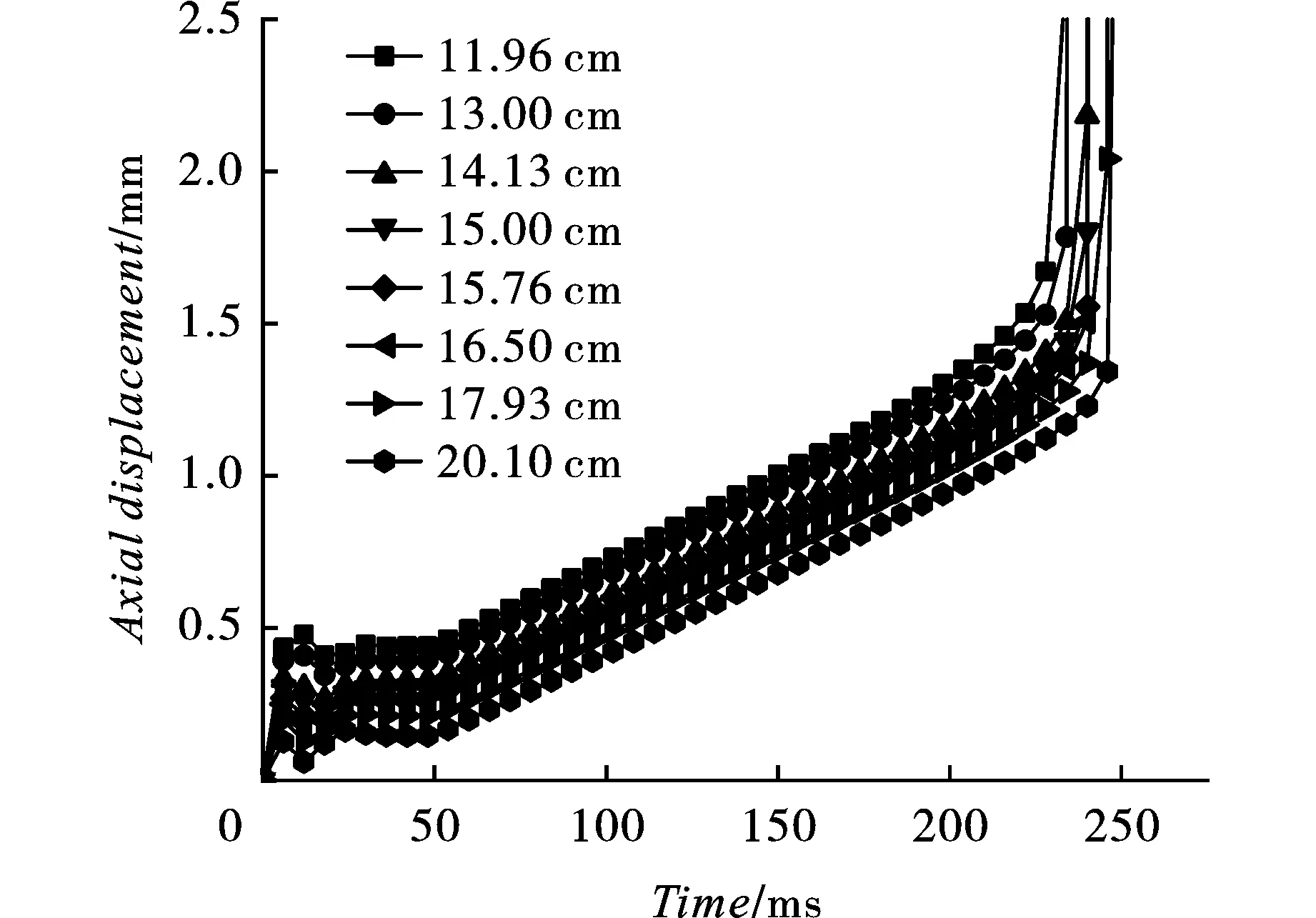
图 8 不同爆距爆炸荷载下方管轴向承载能力持续时间

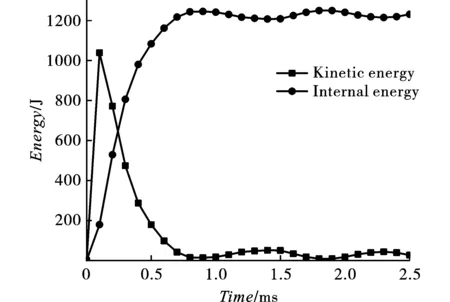
图 9 方管能量吸收

图 10 方管应变能密度和内能密度

施加到方管上的动能被方管迎爆面中心区域吸收，导致迎爆面中心区域凹陷变形，应变能密度高于其他区域1个数量级。方管增加的内能主要由迎爆面中心点位置及周边区域吸收，高出其他区域几个数量级。方管承受近距离爆炸荷载时，方管迎爆面直面冲击波，导致方管迎爆面中心点位置及周边区域严重弯曲变形，耗散很大的爆炸能量。当剩余爆炸能量传递到方管背后，方管周边形成一个近似等压区，方管整体虽有变化，但不能产生大的变形。

3.2 承载能力损伤分析

基于方管残余轴向承载能力，确定方管在爆炸荷载作用下轴向承载能力损伤指数D1，可以定义如下

D1=1-TRes/TIni

(9)

基于方管迎爆面中心点位移，确定方管迎爆面中心点在爆炸荷载作用下径向缩进指数D2，可以定义如下

D2=LDis1/LDia

(10)

基于方管背爆面中心点位移，确定方管背爆面中心点在爆炸荷载作用下径向移出指数D3，可以定义如下

D3=LDis2/LDia

(11)

式中：TRes为遭受爆炸荷载后方管的残余轴向极限加载时间；TIni为方管初始轴向极限加载时间；LDis1为遭受爆炸冲击荷载后方管迎爆面中心点位移；LDis2为遭受爆炸冲击荷载后方管背爆面中心点位移；LDia方管为横截面边长。

D1、D2、D3指数如图11所示。

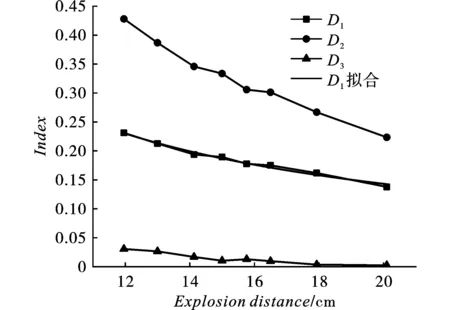
图 11 损伤指数

方管D1最大值为0.2313，最小值为0.1378；D2最大值为0.4281，最小值为0.2235；D3最大值为0.0305，最小值为0.0023。D1曲线与D2曲线，随炸药底部距方管迎爆面中心点距离的增加均成逐渐减小的趋势，且具有相同的凹凸性，但D1曲线的曲率小于D2曲线；D2曲线与D3曲线具有相反的凹凸性。表明，随炸药底部距方管迎爆面中心点距离的增加，D1逐渐减小。D2曲线决定D1曲线总体变化趋势；D3曲线影响D1曲线局部曲率变化。

综合能量吸收分析和承载能力损伤分析，D1采用Allometric1模型进行拟合，曲线方程为

D1=arb

(12)

式中：a=2.30542；b=-0.92573。

该曲线方程仅能计算160 g柱形炸药爆炸荷载下方管轴向承载能力损伤指数D1，计算相似形状，任意当量的柱形药柱爆炸荷载下方管轴向承载能力损伤指数须将爆距r换算为比例距离Z，曲线方程为

(13)

式中：a、b参数值不变。

该曲线方程可作为相似柱形炸药爆炸荷载下该型方管轴向承载能力损伤指数D1的工程算法。

4 结论

方管的轴向承载能力数值模拟值与理论计算值作比较，方管承受横向爆炸荷载后的中部横切面受损尺寸数值模拟值与试验值作对比，误差均在合理范围内，保证建模的合理性。

(1)施加到方管上的爆炸能量大部分转化方管迎爆面中心区域的应变能和内能，中心区域有较大变形，方管整体变形较小；小部分爆炸能量转换成整个方管的振动能量。

(2)随炸药底部距方管迎爆面中心点距离的增加，方管在爆炸荷载下轴向承载能力损伤指数逐渐减小，迎爆面中心点径向缩进指数决定方管轴向承载能力总体变化趋势；背爆面中心点径向移出指数影响方管轴向承载能力的局部变化趋势。

(3)提出了爆炸荷载下特定方管轴向承载能力损伤指数的工程算法，为爆炸荷载下一般方管轴向承载能力损伤指数的工程算法提供了借鉴与参考。