混凝土大坝在水下爆炸作用下的动力响应分析*

庞崇安，刘玉锋，王 震

(1.浙江同济科技职业学院，杭州311231；2.浙江大学 建筑工程学院，杭州310058；3.浙大城市学院，杭州310015)

我国水利工程发达，大坝数目众多，作为关系到民生、国防、环境、能源等重要领域的构筑物，其毁坏的后果的是不堪设想的，中国古代历史上就有多次通过决堰毁坝来达到战略目的的战役，可见大坝的安危影响之重大。现代战争强调精确打击，恐怖袭击或意外爆炸作用导致的失事损失巨大，工程界对大型公共结构的抗爆性能也日益重视，大坝抗爆性能的重要性也不言而喻[1,2]。针对混凝土坝在空中和水下爆炸荷载作用下的作用效应与毁伤模式，国内外学者开展了多项研究。Kalateh基于欧拉-拉格朗日有限元法研究了空中爆炸冲击荷载作用下混凝土坝的动态响应[3]，并对大坝的不同高度和起爆距离进行了参数化分析。文献[4]比较了水下和空中爆炸时大坝的动态响应认为水下爆炸冲击荷载破坏效应更为严重，容易造成大坝结构的破坏。文献[5]用数值模拟研究蓄水位和炸药位置等因素对冲击波传递、大坝动态响应、混凝土损伤因子等方面的影响。针对水下接触爆炸对大坝的动态响应和破坏特征，Xu[6]、Wang[7]、Li等研究认为初始静水压力[8]、初始应力场对混凝土重力坝的冲击波传播、爆炸振动和破坏模式具有不可忽略的影响。Ren等基于离心机实验[9]，建立三维数值模型并进行参数化分析，研究了混凝土重力坝在非接触式水下爆炸攻击下的破坏和失效情况。Moradloo等研究了拱形混凝土坝在水下爆炸作用下的动态响应和损伤特性[10]，结果表明离爆源越近，爆炸的损害越早，而对于一定数量的炸药，大坝上游面位移随爆炸深度的增加而增加。文献[11]总结了爆炸荷载分类和目前常用的技术路线，并指出各种爆炸条件需要关注不同问题。然而，由于混凝土大坝在水下爆炸作用下的破坏模式较为复杂，有必要针对混凝土大坝在水下爆炸荷载作用下的动力响应作进一步的深入研究。

利用动力显式有限元软件ANSYS/LS-DYNA对水下爆破荷载作用下的大坝进行数值模拟，考虑其流固耦合效应，研究分析了考虑重力和不考虑重力两种模型下大坝在爆破荷载下的动力响应，以期为实际大坝工程动力分析及抗爆设计提供参考。

1 材料模型与参数

1.1 炸药

炸药采用LS-DYNA中的* MAT_HIGH _EXPLOSIVE _BURN，炸药状态方程采用JWL方程

(1)

式中：A、B、R1、R2、ω为常数；V为体积；E为能量。文中具体参数如表1所示。其中:ρ为密度;D为起爆速度;PCJ为爆压。

表 1 TNT炸药模型参数

1.2 水介质

对高压下的水体采用Gruneisen方程

(γ0+αμ)E

(2)

式中：P为爆轰压力；E为单位体积内能；μ=ρ/ρ0-1；C为声音在水中传播速度；S1～S3、γ0为状态方程系数，a为γ0的一阶矫正系数。本文中水介质的具体参数如表2所示。其中ρ为某个时刻的密度，E0为初始内能，V0为相对体积。

1.3 空气介质

对气体一般采用多方状态方程

P=(C0+C1μ+C2μ2+C3μ3)+

(3)

式中：C0～C6为常数；V为相对体积；E为单位体积内能，具体取值如表3所示。其中:ρ为密度;E0为初始内能;V0为初始体积。

表 2 水介质参数

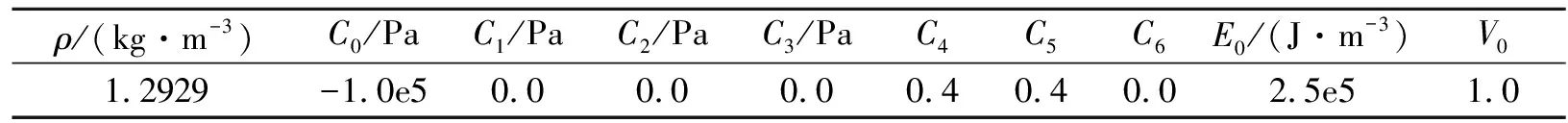
表 3 空气介质参数

1.4 混凝土

混凝土采用HJC(Holmquist-Johnson-Cook)本构模型[12]，在LS-DYNA中为*MAT_JOHNSON_HOLMQUIST_CONCRETE，该模型反映混凝土在大变形、高应变情况下的特征，并能模拟其损伤过程。混凝土的等效强度是关于静水压力、混凝土应变率和损伤因数的函数，其中混凝土材料的损伤累积主要来自于塑性体积应变、等效塑性应变和静水压力的影响，具体参数见表4。其中:ρ为密度;G为剪切模量;A为标准化的凝聚力强度;B为标准化的压力硬化强度;C为应变率系数;N为压力硬化指数;Fc为准静态单轴抗压强度;T为最大静水拉伸压力;ETS0为准静态阈值应变率;EFMIN为断裂塑性应变;SFMAX为标准最大强度;PC为压碎应力;UC为压碎体积应变;PL为锁定压力;UL为锁定体积应变;D1～D2为损伤常数;K1～K3为压力常数;FS为失效塑性应变。

表 4 混凝土HJC模型参数

1.5 岩石

岩石采用双线性弹塑性模型，LS-DYNA中材料类别为*MAT_PLASTIC_KINEMATIC。具体参数如表5。其中:ρ为密度;E为弹性模量;PR为泊松比;SIGY为屈服强度;ETAN为强化模量，强化系数β=1代表采用等向强化模型;FS为破坏有效塑性应变。

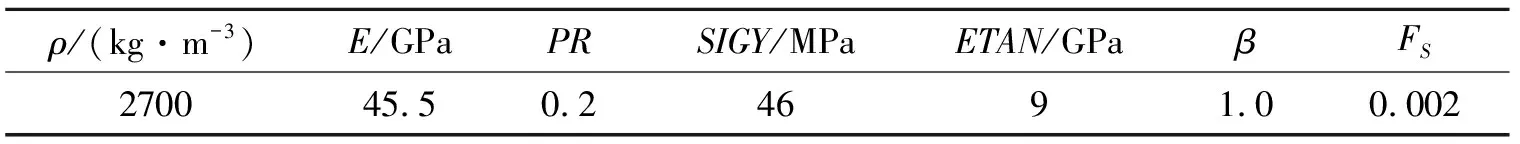
表 5 岩石参数

2 建立有限元模型

作为本文研究对象的大坝，坝体高85 m，坝顶宽15 m，坝底宽60 m，坝坡高65 m。大坝左侧为水，水深75 m，水面以上至坝顶高度为空气，此部分流体域宽度取130 m。大坝以下为基岩，基岩深度取170 m，宽300 m，左边界与流体域齐平。炸药位于水体表面，与大坝接触处。大坝和基岩直接共节点，即认为属于刚接，流体域和固体域之间是两个分离的体块，不需设置接触，但为使固体发生大变形后流体能填补空档，在流体域深入固体部分4 m，重叠部分用水介质填充。将基岩的左面、右面和底面节点的三个平动自由度约束。计算模型的几何如图1(a)所示。本文采用扫略网格方法划分模型，在炸药附近将网格划分得较细，往外每隔一段距离将网格大小放大，共放大两次，最后得到的有限元模型如图1(b)所示。在厚度方向，尝试了数种划分方式，典型方式包括厚度1 m，划分为一个单元和厚度2 m，划分为四个单元，两者的结果见图2。可以发现2 m厚度模型由于爆炸产生的缺口明显大于1 m模型，其应力极值(超过100 MPa)也远大于1 m模型，甚至远高于混凝土的正常极限强度。且由于极值过大，云图主要集中在缺口附近，对其他区域的应力分布不能很好地显示。综合以上考虑，并结合相关文献[13-15]，将建模方法确定为厚度方向1 m，划分为一个单元。

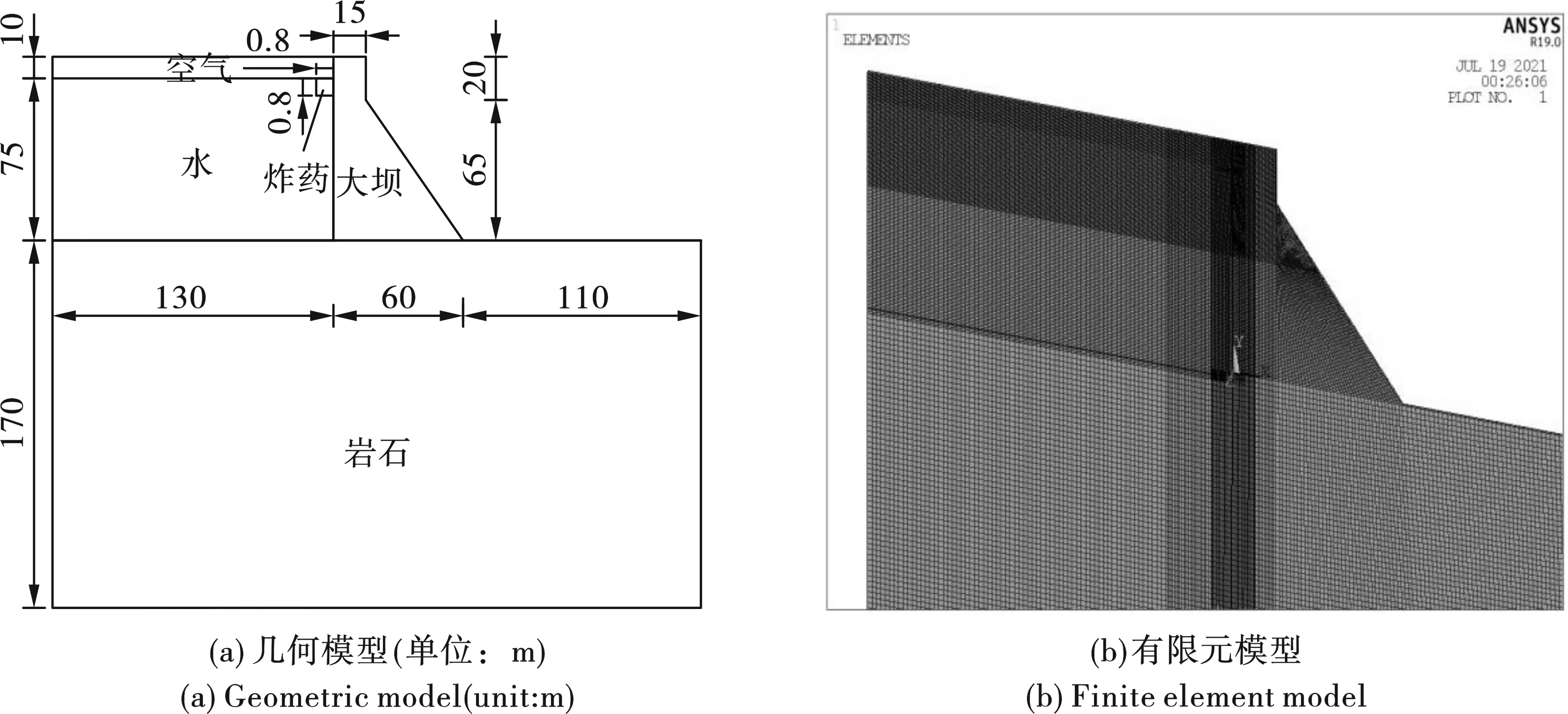
图 1 大坝结构模型

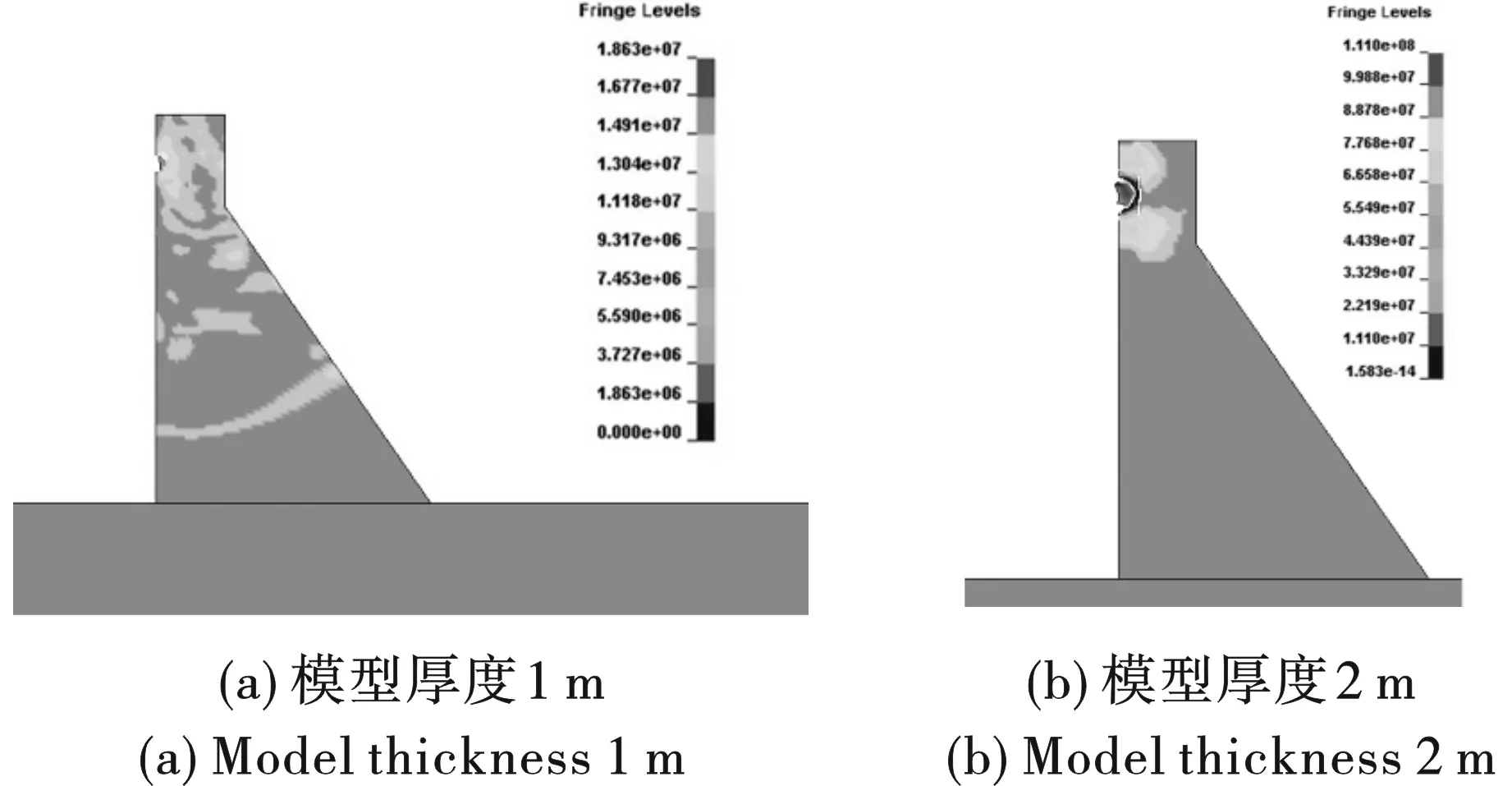
图 2 两种厚度下爆炸后16ms时应力云图

对于固体计算常用的Lagrange算法而言，一个单元内只能是一种物质，即单元是附在物质上的。若炸药、空气单元采用Lagrange法，很容易在爆炸过程发生严重的畸变，往往使计算中断。对于ALE算法，一个单元中可包含不同的材料，并能在空间网格中完成物质的输送。建模时，炸药、水和空气三种材料可采用欧拉网格建模，单元使用多物质ALE算法。

在k文件中，添加关键字*CONTRAINED_LAGRANGE_IN_SOLID定义流固耦合，耦合方式采用罚函数的方法，需要提醒的是，此关键词卡中前两个参数分别指流体域和固体域，需要事先定义PART组，可在前处理中定义或修改*SET_PART_LIST完成。

计算的能量控制参数在前处理中用EDENERGY命令设置，本报告的计算模型只打开石墙能(Stonewall Energy)和滑移能(Sliding Interface)，此外，体积黏性系数取默认值，无需特别设置。用EDCTS控制时间步迭代大小，此值过大会影响计算收敛，有高能炸药时缺省为0.67，本文中取0.6。在k文件中添加关键字*CONTROL_ALE来控制流固耦合时的相关参数设置，采用默认值。最后在k文件中添加关键字*INITIAL_DETONATION来定义起爆点和起爆时间，将起爆点位置定义在炸药域的中心，无重力时起爆时间定为0，有重力时起爆时间为1.2 s。

3 大坝水下爆炸荷载动力响应

修改前处理器生成的k文件，放入LS-DYNA求解器中计算，可得到爆炸后大坝随时间变化的响应，除了观察其应力分布之外，另外提取几个典型位置点，读取其时程历史数据，典型位置的分布如图3所示。

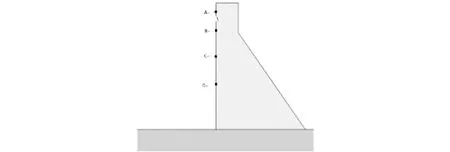
图 3 典型位置点分布

3.1 未考虑重力模型

取炸药当量1 t(炸药当量根据炸药密度乘体积算得)位于近水面紧靠大坝处，大坝上的Von-Mises应力云图如图4所示。

模型的Von-Mises应力云图变化为与炸药相邻的坝体先被炸出一个裂口，即一小块混凝土达到破坏准则而退出工作，应力波从此处向外扩散，7 ms时四种模型的应力波均扩散至整个坝顶区域，之后坝顶区的应力水平维持在一个较高的水平，而向下传播的应力波逐渐扩散并衰减。整个过程中，与缺口相邻的上方和下方，以及坝坡转角处是应力最大的位置，这也是容易产生应力集中的地方。爆炸初始大坝上的应力极值可超过50 MPa，后续极值稳定在10～30 MPa之间震荡。

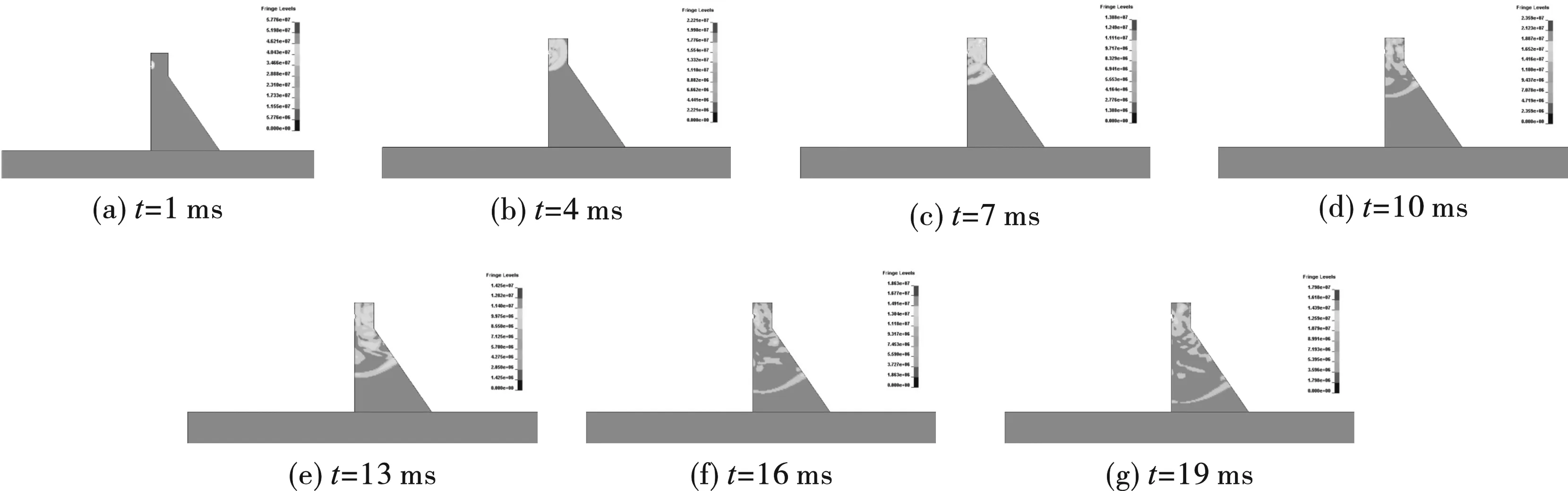
图 4 无重力爆炸后不同时刻Von-Mises应力云图

3.2 考虑重力后的模型

LS-DYNA中，通过定义加载曲线施加重力，LS-DYNA是动力分析软件，用其来进行重力计算需要等待重力荷载扩散并稳定，即所谓的“拟静力”，在此过程中，必须用关键字*DAMPING_PART_MASS_SET引入阻尼，否则结构会不断震荡而不能达到稳定。重力作用下和爆炸后的应力云图如图5所示。

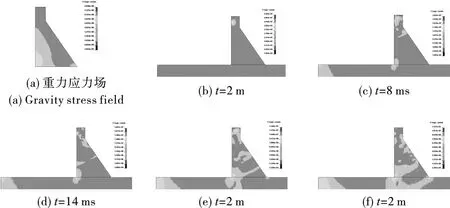
图 5 重力作用下爆炸后不同时刻Von-Mises应力云图

重力作用下，坝踵处有着最高的应力，可达数兆帕，坝趾处也有一定应力集中的现象，但程度小于坝踵。爆炸发生后冲击波扩散的趋势仍然比较明显，但爆炸使混凝土破碎而产生的缺口消失了，过程中大坝上的最高应力水平和未施加重力的模型相差不大，爆炸初始时高达50 MPa以上，随后衰减到10～20 MPa，说明冲击波本身的应力远大于重力造成的应力大小，但是坝踵区在应力波到达之前就有与之相近的应力水平，说明重力在该处造成的应力集中水平与爆炸的应力波约处于一个量级。然而，应力波传到坝踵与重力叠加后，坝踵的应力水平并未上升，约3～8 MPa，与仅在重力作用下该处的应力水平(4～8 MPa)相比并无显著变化，说明重力产生的应力与爆炸产生的应力在该处并不是线性叠加的关系，且偏于安全，但由于坝踵是影响大坝整体安全稳定的关键部位，仍有必要对其进行较为保守的估计。

3.3 未施加重力和施加重力模型对比

图6是无重力作用下典型位置的位移时程曲线和压强时程曲线。由于含重力模型在爆炸前各单元就有初始位移，为了更直观比较爆炸后的响应的变化，将含重力模型的位移减去重力作用下的初始位移。

由图6(a)可知，无重力模型中各单元位移总体随时间增大，而有重力模型的单元位移则减小，说明爆炸产生的位移与重力产生位移有一部分互相抵消，且这种抵消与冲击波的传递方向无关。两个模型下爆炸缺口上方的位移都大于缺口下方，而位于坝体左侧中部和中下部两个距离炸药较远的点的位移较小，可以忽略。含重力模型爆炸后离炸药较近的典型位置单元位移变化量绝对值明显小于无重力模型，说明重力对爆炸产生的动力响应产生了一定的抵抗作用，且不是线性叠加关系。

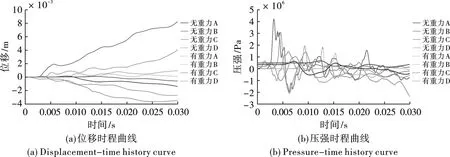
图 6 典型位置单元时程曲线

无重力模型中，四个典型位置的压强极值分别约4 MPa、3 MPa、2 MPa和1.5 MPa，缺口两侧的典型位置有多个压强峰值，说明冲击波产生过多次反射，但极值均发生在第一个峰值处，且发生时间与距离炸药距离呈负相关。重力造成的初始压强相对爆炸来说较小，但有重力模型的四个典型位置的压强峰值都小于无重力模型，这从另一个方面说明重力的存在减轻了爆炸的作用。

4 结论

本文对考虑重力和不考虑重力两种模型的大坝水下爆炸冲击荷载及其动力响应进行数值模拟，得到以下主要结论：

(1)爆炸初始产生的缺口是冲击波扩散的起点，冲击波会多次反射，缺口和坝坡转角处是容易产生应力集中处。爆炸初始时最大应力可超过50 MPa，之后在10～30 MPa之间震荡。

(2)未考虑重力时，各点位移总体上呈随时间增长的趋势，离炸药较近的点位移较大。不同点的压力都在爆炸后冲击波第一次反射时达到极值，且极值随离炸药距离的增大而减小，可将第一次反射压力作为爆炸冲击荷载。

(3)重力作用下坝踵应力最大，考虑重力时爆炸后大坝上没有明显缺口，但应力极值并无显著变化。

(4)重力产生的位移和压力对爆炸效应起抵抗作用，但(尤其在离炸药接近的区域)两者并不是线性叠加关系。