以“形”换“数”,化繁为简
闫旭 汤琼 魏莉莎 杨婕

摘要:数形结合思想在数学学科中扮演着重要角色,它贯穿整个初中数学,尤其在解决含参一元一次不等式组问题时,经常需要运用数形结合的方法解题.文章针对不同类型加以举例分析说明与总结.
关键词:数形结合;一元一次不等式组;含参
数形结合思想是初中數学教学中广泛应用的一种思维方式,它是代数学与几何学相互渗透的产物,具有较高的解题应用价值.数形结合思想源于“直观形象”,表现为“经验形态”[1],它能够化繁为简,将抽象转变成具象,辅助学生解题.
初中生面对有关“动点、变量、含参”等具有不确定性的动态问题时,普遍会感到困惑,这是他们的认知从低阶到高阶、由具象到抽象提升道路上的必经之路.在“解一元一次不等式组”教学中,教师引导学生运用数形结合思想,借助数轴找到不等式组的解集.那么遇到含参问题,也可利用数轴,把原本抽象的字母、不等关系等具体表示出来,从而简化题目,准确求解.下面以“含参一元一次不等式组”为例,说明如何利用数形结合思想来教学.
1 数轴直接判断型
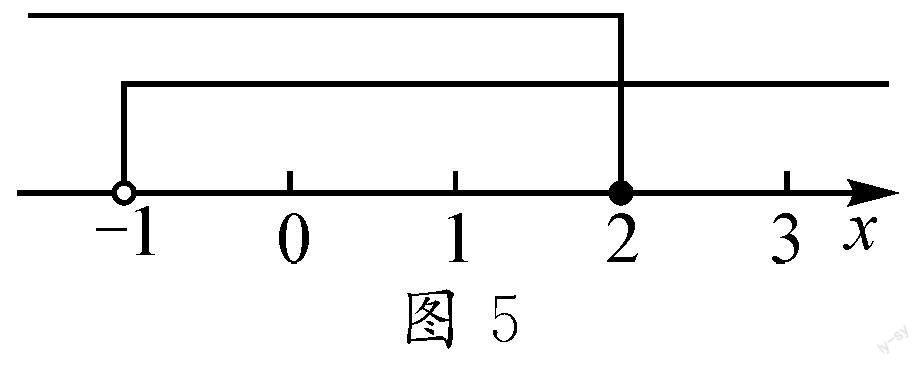
解集是x
小结:此类型问题一般表现为问法直接,且只有一个不等式含参,求参数取值范围.一般思路是先整理不等式组,在数轴上画出确定的不等式的解,再根据有解或无解条件大致表示出含参数的不等式的解,最后确定临界值即等号的取舍.
2 整数解分析型
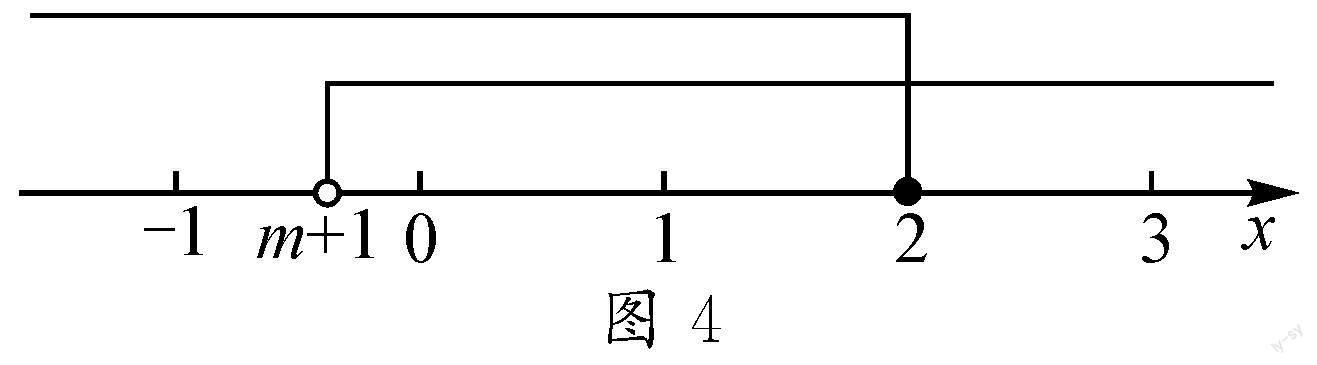
解析:由不等式组m+1 A.-3 B.-3≤m<-2 小结:此类型问题一般表现为,已知整数解个数,且只有一个不等式含参,求参数的取值范围.一般思路是先整理不等式组,在数轴上画出确定的不等式的解,根据确定的一支和整数解个数推理出另一个不等式解的临界值在哪两个整数之间,最后确定临界值即等号的取舍. 3 分类讨论型 A.a>5或a<2 B.a≥5或a<2 C.a>5或a≤2 D.a≥5或a≤2 解析:解原不等式组,得a 如图10,当a 如图11,当a 综上,a≤2或a≥5.故选:D. 小结:此类型问题一般表现为解集不在某个封闭的范围内,或题目条件不明确,而是以“整数解的和”的形式指出有几个整数解.一般思路是先整理不等式组整理,根据题目条件确定不同情况,再借助数轴对每种情况具体讨论,最后综上得出答案. 4 总结 数形结合是一种辅助解题的思想方式,不能误解为完全依赖画图得出答案.在“含参一元一次不等式组”解题与教学时,要先对题目进行深入分析和思考,判断问题类型,理清条件,再借助数轴来直观表示,快速准确建立含参不等式,最后考虑端点问题[2].当然,数学是一门灵活的学科,以数轴的“形”来替代“数”辅助解题与教学并非必须,也可以采用口诀“大大取大、小小取小、大小小大找中间、大大小小找不了”直接判断,需要结合实际问题灵活运用. 参考文献: [1]王永强.数形结合思想的教学过程与阶段性表现形态的研究[J].中学数学月刊,2022(11):16-19. [2]徐树光.含参一元一次不等式(组)问题求解策略[J].中学数学,2022(22):58-59.

