正交铺设复合材料层合圆柱壳自由振动分析的辛空间波方法
韩少燕, 李榆银, 高汝鑫
(1. 西安交通大学城市学院 机械工程系,西安 710018;2. 株洲中车时代电气股份有限公司,湖南 株洲 412001;3. 北京理工大学 先进结构技术研究院,北京 100081;4. 大连理工大学 工业装备结构分析国家重点实验室,大连 116024)
复合材料层合圆柱壳因其加工简单、比强度和比刚度高、力学性能优异等特点,被广泛应用于航空航天、舰艇、油气输送等各个领域。在工作环境中,圆柱壳结构会受到复杂的动力载荷作用,从而产生有害振动甚至共振行为,对结构的安全以及内部设备的工作状态产生不利的影响。因此,准确快速地分析复合材料层合圆柱壳的动力学特性是十分必要的。
在过去的几十年,学者们提出了不同的壳体理论以及大量的计算方法,这些理论可以在Leissa等[1-3]的书中找到详细的介绍。壳体的理论主要分为3种:经典壳体理论(classical shell theory, CST)、一阶剪切变形理论(first-order shear deformation theory, FSDT)和高阶剪切变形理论(high-order shear deformation theory, HSDT)。CST理论是针对薄壁均质壳结构提出的,忽略了横向剪切变形,其要求壳体的厚度远小于其他两个维度的尺寸。CST理论根据满足Kirchhoff假设的薄板扩展而来,根据不同的假设和简化,发展出了各种薄壳理论,例如Love壳理论、Flügge壳理论、Sanders壳理论和Donnell壳理论等。随着复合材料的发展,CST理论也被扩展到薄壁层合壳的分析中。Lam等[4]通过引入参数,将上述4种薄壳理论纳入到统一的框架下,通过设定参数的值,可退化到不同的薄壳理论,用于旋转薄壁层合壳的动力学分析中。过去的几十年,基于薄壁层合壳体理论的数值方法也得到了充分的发展[5-6]。
一般情况下,相比于各向同性壳,层合壳的厚度更大,剪切刚度更小,考虑横向剪切的影响是必要的。FSDT考虑了横向剪切变形的影响,其假定横向剪切应变沿厚度方向为常数,学者们基于FSDT发展了很多适用于中厚壳的动力学分析方法[7-12];HSDT放松了厚度方向上横向剪切应变为常数的假定,进一步发展了壳体理论;此外,为考虑横向正应力的影响,基于HSDT的三维(3D)壳体理论[13-14]也被提出和发展。需要指出的是,虽然学者们基于FSDT和HSDT发展了众多壳体动力分析方法,但是这些方法的推导和使用往往比较复杂,且一般情况下对于薄壁层合壳的分析,CST理论的精度完全满足工程需求,故对于基于CST的薄壁层合圆柱壳的动力分析方法的研究仍然受到学者们的广泛关注。
Yao等[15]将分析力学的Hamilton理论体系引入到弹性力学问题的求解中,其将弹性力学问题从Lagrange体系转化到辛空间下的Hamilton体系,打破了传统求解方法的局限,得到了适用于多种弹性力学问题的理性解析解。许多学者在该理论体系下进行了深入研究。Li等[16]提出了矩形薄板自由振动的辛叠加方法,给出了有/没有弹性基础矩形薄板自由振动的解析解。Zhou等[17]利用Hamilton体系研究了圆板和环板的自由振动问题。Tong等[18]基于Donnell和Reissner壳体理论利用辛方法给出了任意边界条件下圆柱壳自由振动的精确解。Gao等[19]针对正交各向异性圆柱壳的自由和强迫振动问题,提出了辛空间波传播方法。Pan等[20-21]针对静水压下加环肋和双层加筋加环肋圆柱壳的强迫振动问题,发展了辛空间波传播方法。
本文针对正交铺设复合材料层合圆柱壳的自由振动分析,提出了辛空间波方法。首先通过选取合适的状态向量,将物理空间中的弹性力学三大方程转换成辛空间中的振动控制方程,实现了问题的降维和变量的分离;其次利用分离变量法将层合圆柱壳的自由振动问题转化为Hamilton体系下的辛本征值问题,根据辛空间波形与圆柱壳模态的对应关系,得到不同边界条件下的自由振动波数;最后求解圆柱壳自由振动问题的代数方程组,即可得到正交铺设复合材料层合圆柱壳的固有频率和模态。数值算例对比了本文方法和其他方法的计算得到的圆柱壳固有频率,验证了本文方法的有效性,指出了本文方法在处理非两端简支边界条件时的误差来源。
1 层合圆柱壳的基本方程
考虑如图1所示的复合材料层合圆柱壳,圆柱壳的长度、中面半径和厚度分别以L、R和h表示。使用固定在圆柱壳上的柱坐标系(x、θ和r)描述圆柱壳的运动,见图1。
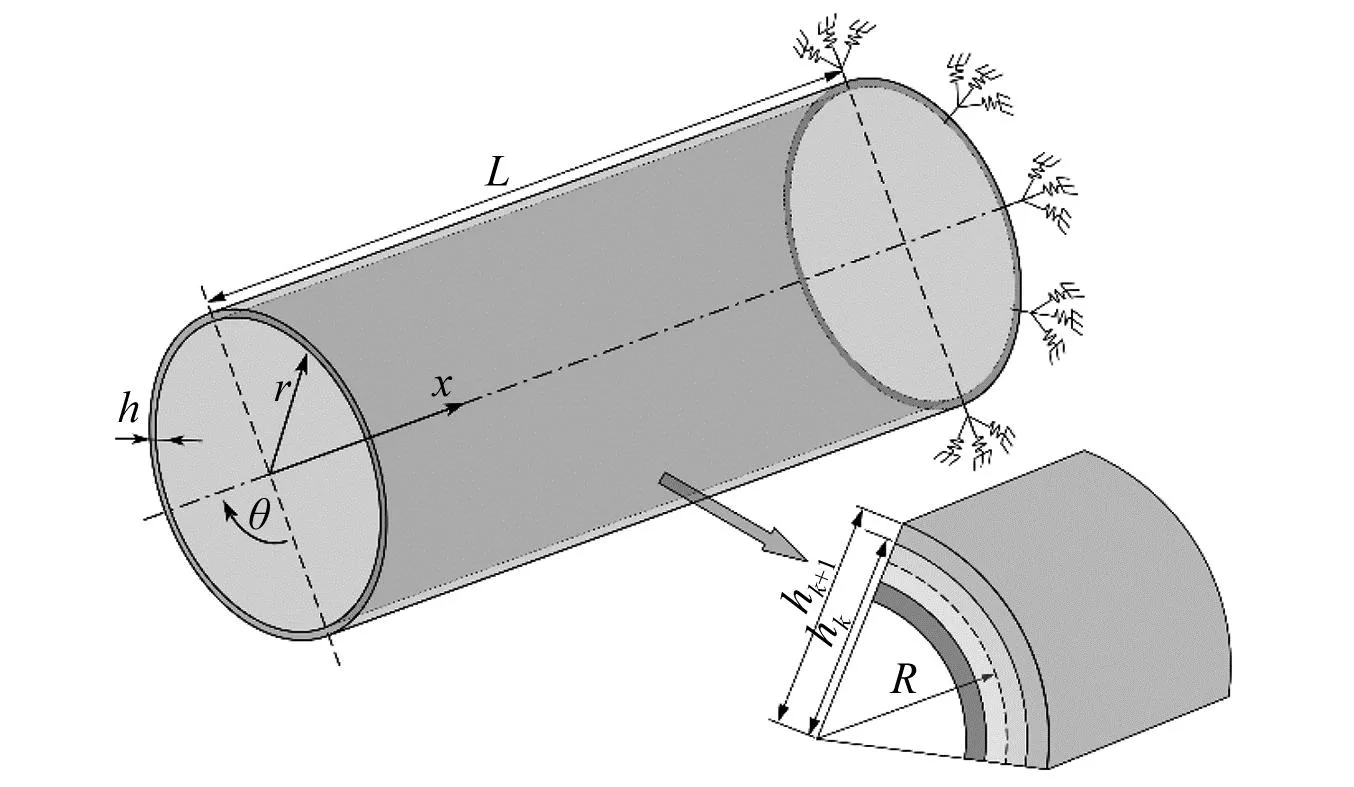
图1 正交铺设复合材料层合圆柱壳示意图Fig.1 Schematic diagram of a thin composite laminated circular cylindrical shell
圆柱壳中面沿3个坐标方向的位移分别记为u、v和w,中面绕x和θ轴的旋转分别记为φx和φθ。复合材料层合圆柱壳由若干单层圆柱壳组成,且认为各层间界面是刚结的。
1.1 几何方程
根据Kirchhoff-Love薄壳理论,圆柱壳中面上的膜应变分量和曲率应变分量可以分别写为
(1)
(2)
其中,
(3)
(4)
第k层上任意一点处的应变-位移关系可以写为
(5)
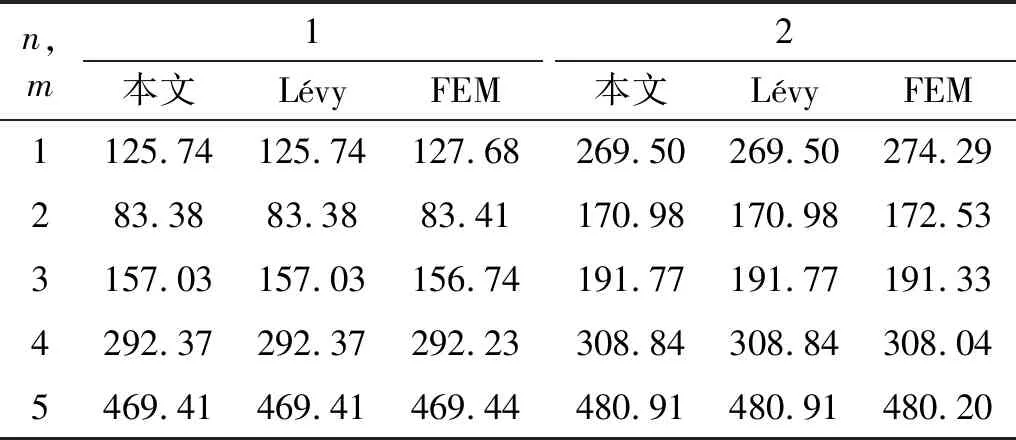
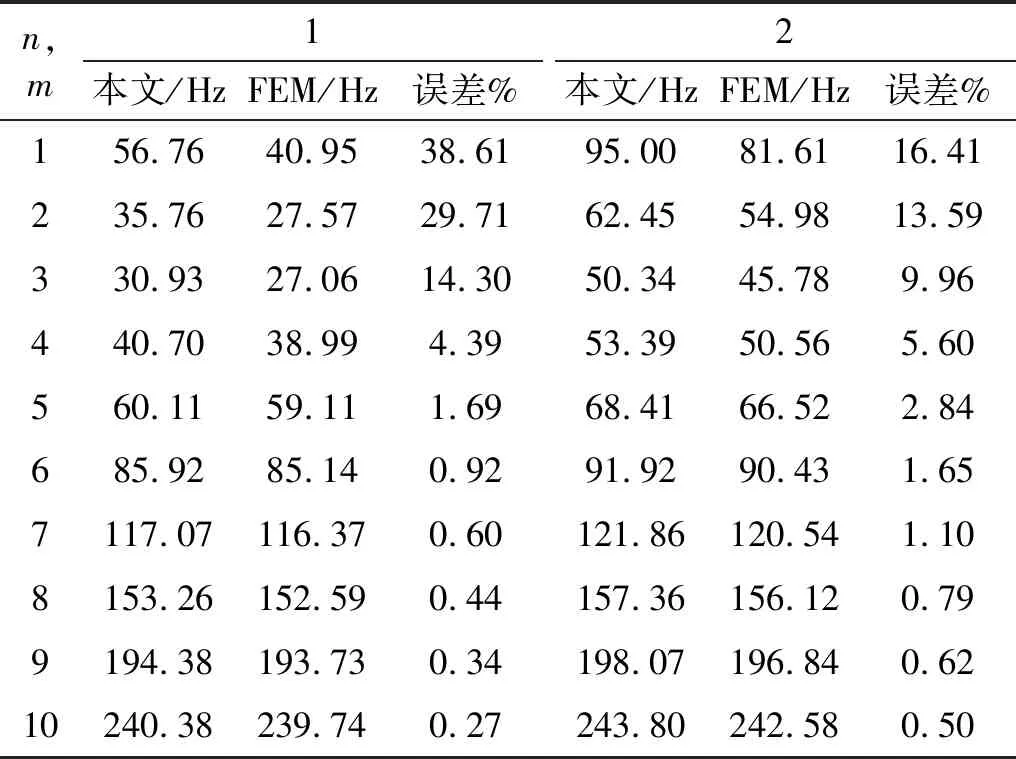
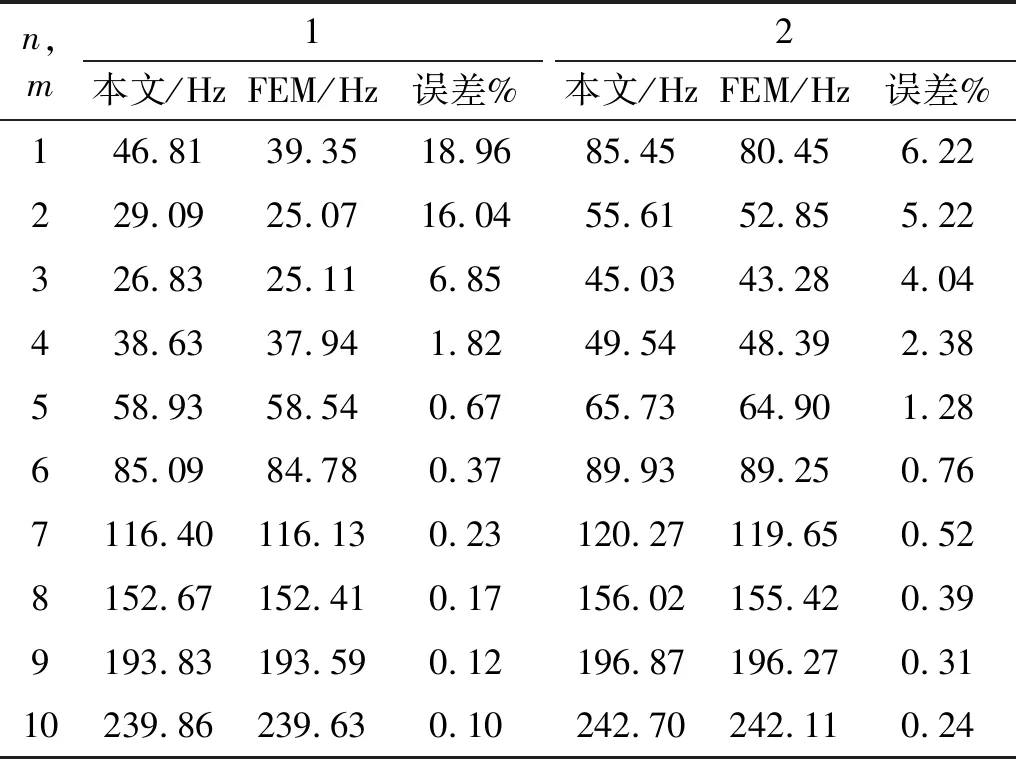
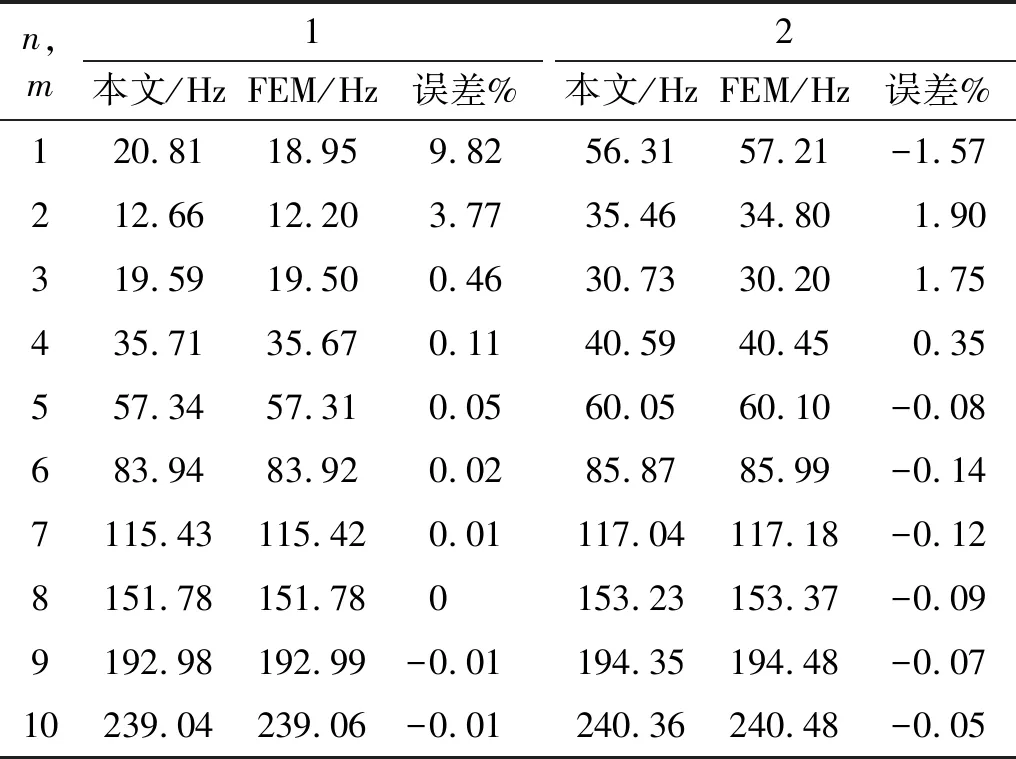
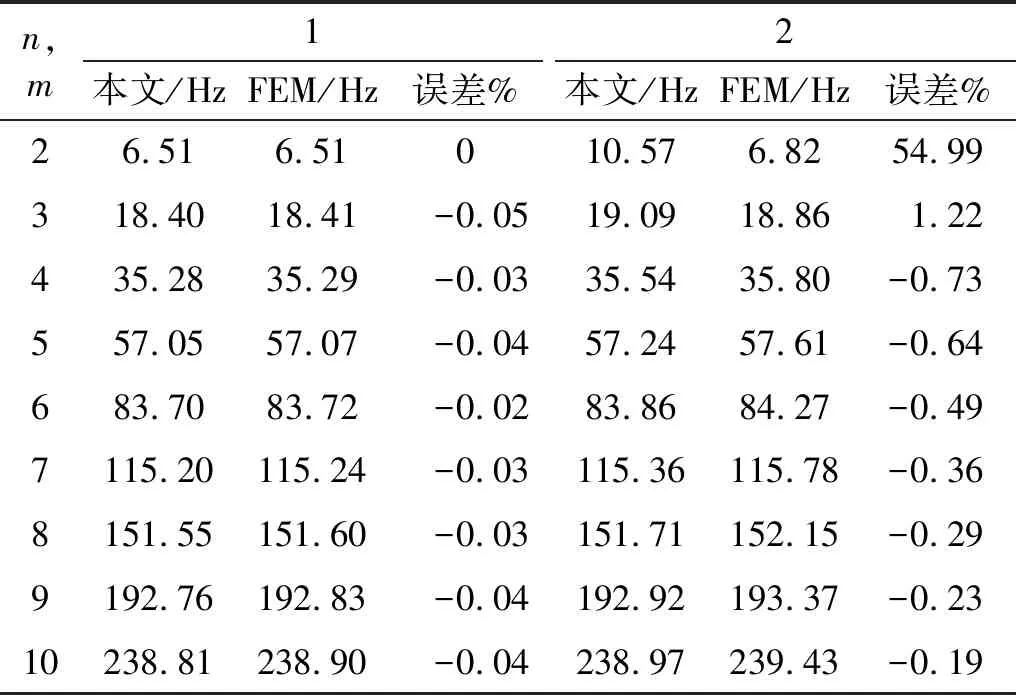
式中:hk+1 根据广义胡克定律,第k层的应力-应变关系可以写为 (6) (7) 式中,Aij、Bij和Dij,i,j=1,2,6分别为第k层的膜刚度、膜弯耦合刚度和弯曲刚度。对于正交铺设复合材料层合壳体,有A16=A26=D16=D26=B16=B26=0。 根据Kirchhoff-Love薄壳理论,层合圆柱壳自由振动的运动方程可以写为 (8) 式中:ω为圆频率;ρ为圆柱壳的质量密度。 将式(7)写为矩阵的形式有 F=Dε (9) 取位移基本变量为q={uvwφx}T,可将ε重新写为以下形式 (10) 其中, (11) (12) 复合材料层合圆柱壳的Lagrange密度函数可以表示为 (13) 由Legendre变换可得 (14) (15) 将式(15)移项可得 (16) 其中, (17) (18) 将式(17)和式(18)展开可写为 (19) (20) (21) 则式(16)被修正为 (22) 其中, (23) (24) (25) 此时,将式(22)移项可得 (26) 对式(8)进行移项,并结合式(3)和式(4),可得到 (27) 其中, (28) (29) (30) 将式(26)和(27)写成统一的形式,有 (31) 其中, (32) (33) (34) (35) HC=Cγ (36) 从式(31)~式(36)容易看出,矩阵HB和HC是对称矩阵,所以矩阵H为Hamilton算子矩阵。式(33)中矩阵各元素的具体表达式见附录A。 式(31)为齐次微分方程,其可利用分离变量法来求解,状态向量z可以表示为以下形式 z(x,θ)=η(θ)eμx (37) 式中,μ为轴向的波传播参数。式(37)实现了变量x与θ的分离。圆柱壳在周向具有周期性,所以η(θ)可以写为 η(θ)=φmeimθ,m=0,±1,±2,… (38) 将式(37)~式(38)代入式(31)得到 (39) 将式(39)移项,可以得到 (40) 式(40)有非平凡解的条件为 (41) 式(41)可以进一步简化为 λ3+c1(μ)λ2+c2(μ)λ+c3(μ)=0 (42) 其中, λ=ω2 (43) 式(42)是一个一元三次方程,其可以被解析地求解,其中c1(μ)、c2(μ)和c3(μ)是由轴向波数μ决定的系数。式(42)存在3个根,分别对应圆柱壳在3个方向上的自振频率,其中值最小的根对应于圆柱壳的弯曲振动。 根据驻波的定义,圆柱壳内产生驻波时,入射波与返回波的相位应该相同,即 2μL+i(φr+φl)=2iNπ (44) 式中,N为整数。所以发生驻波时的波传播参数μN应满足 (45) 式(45)即为自然模态对应的波传播参数的值,给定一个整数N,即可得到一个相应的波传播参数μN,然后将该波传播参数μN代入到式(42)并求解,即可得到圆柱壳的自然频率。 将入射波与返回波的波幅叠加后即可得到自然模态,以两端简支的圆柱壳为例,自然模态可以写为 ψm,N=φmeimθ(eμNx-e-μNx) (46) 由式(31)和式(32)可以看出,本文方法可以解析地得到圆柱壳的自然频率,具有较高的精度和效率;另外,利用式(38)、式(39)和式(46)可以快速地得到圆柱壳的自然模态。 本文方法可进一步扩展到任意边界条件下层合圆柱壳的强迫振动分析,相关工作正在开展中。 根据Reddy的研究,Lévy方法可以解析地求解两端简支的层合圆柱壳的振动问题,然而Lévy方法无法求解其他(非两端简支)边界条件下的层合圆柱壳的振动问题。FEM(finite element method)可以容易地处理各种复杂的边界条件,然而FEM的计算成本较高,尤其对于求解高阶模态,FEM需要划分精细的网格才能准确地描述高阶模态,进一步加剧了计算负担。 本章首先考虑两个两端简支边界条件下的层合圆柱壳,对比本文方法、Lévy解、FEM计算得到的结果以及已有文献中的结果,证明本文方法的正确性。其次依次考虑两端固支-固支(CC)、固支-简支(CS)、固支-自由(CF)和自由-自由(FF)边界条件下的正交铺设复合材料层合圆柱壳,对比利用本文方法的和FEM计算得到的自振频率,展示本文方法处理非两端简支边界条件的能力,解释本文方法结果的误差来源。本章使用FEM计算圆柱壳的自振频率时采用Lanczos算法作为矩阵特征值分解方法。 考虑一个正交铺设的复合材料层合圆柱壳,圆柱壳两端简支。其几何尺寸如下:R=1.0 m、L/R=5、h/R=0.1,两层,铺设方案为[0°/90°]。每层的材料属性为:质量密度ρ=1 532 kg/m3、两个主方向上的弹性模量E1=124.5 GPa和E2=10.2 GPa、剪切模量G12=6.3 GPa、泊松比ν12=0.34。 根据Qatu和Reddy的研究,两端简支边界条件下存在Lévy解。分别利用本文方法、Lévy解和FEM求解复合材料层合圆柱壳的固有频率,结果如表1所示,其中m和n分别表示圆柱壳在θ方向上的波数和x方向上的半波数。 表1 两端简支边界条件下不用方法计算的自振频率 由表1可知,本文方法计算的结果与Lévy解一致,与FEM计算结果的误差也非常小,具有较好的一致性。验证了本文方法对两端简支复合材料层合圆柱壳自由振动分析的正确性。 以m=3,n=2为例,利用本文方法和FEM分别计算圆柱壳的模态,其中本文方法采用和FEM相同的网格进行渲染,如图2所示。可以看到,本文方法和FEM得到的圆柱壳模态形状吻合很好,进一步验证了本文方法对两端简支复合材料层合圆柱壳模态计算的正确性。 图2 两种方法计算得到的模态对比Fig.2 Comparison of the natural frequency calculated using FEM and the present method 接下来,考虑文献[4]中给出的例子,两端简支的正交铺设复合材料层合圆柱壳,几何参数为:R=1.0 m、L/R=5或10、h/R=0.002,三层,铺设方案为[0°/90°/0°],材料属性为:质量密度ρ=1 643 kg/m3、两个主方向上的弹性模量E2=7.6 GPa和E1=2.5E2、剪切模量G12=4.1 GPa、泊松比ν12=0.26。 表2 两端简支正交铺设复合材料层合圆柱壳的无量纲频率参数 为了进一步验证本文方法的正确性及对不同边界条件的适用性,本节考虑不同边界条件下的正交铺设复合材料层合圆柱壳。圆柱壳尺寸为R=1.0 m、L/R=5、h/R=0.05,由三层单壳正交铺设而成,铺设方案为[0°/90°/0°]。每层的材料属性为:质量密度ρ=1 700 kg/m3、两个主方向上的弹性模量E1=25.0 GPa和E2=1.0 GPa、剪切模量G12=0.5 GPa、泊松比ν12=0.25。圆柱壳的两端边界条件分别考虑为:CC、CS、CF和FF。不失一般性,圆柱壳的周向波数取m=1~10,轴向半波数取n=1~2。此处不对比刚体模态,故FF边界条件下,圆柱壳的周向波数取m=2~10,轴向半波数取n=0~1。 由于在非两端简支的情况下,不存在理论的Lévy解,所以此处将FEM计算得到的结果作为参考解。分别利用本文方法和FEM计算复合材料层合圆柱壳的自振频率。4种不同边界条件下两种方法计算得到的自振频率的对比,如表3~表6所示。其中m和n分别为圆柱壳在θ方向上的波数和x方向上的半波数,表中给出的误差为本文方法与FEM结果的相对误差百分比。 表3 CC边界条件下不同方法计算的自振频率 表4 CS边界条件下不同方法计算的自振频率 表5 CF边界条件下不同方法计算的自振频率 表6 FF边界条件下不同方法计算的自振频率 由表3~表6可知,当周向波数较小时,本文方法计算的自振频率结果误差较大,这是由非简支边界条件下近场波的影响导致的。近场波是衰减波,正如表中数据所展示的,随着周向波数的增加,近场波急剧衰减,从而使得本文方法计算的结果与FEM得到的结果吻合的非常好。 本文针对正交铺设复合材料层合圆柱壳的自由振动分析提出了辛空间波方法。该方法在辛空间中建立了复合材料层合圆柱壳的振动控制方程,实现了问题的降维和变量的分离,进一步利用辛空间波形与模态的对应关系求解自由振动问题的多项式方程,得到复合材料层合圆柱壳的固有频率和模态。本文方法可以处理不同的边界条件,数值算例表明,对于两端简支边界条件,本文方法总是能给出高精度的结果;对于其他边界条件,近场波的影响导致本文方法存在一定的误差,然而随着轴向波数的增加,近场波的影响减小,此时本文方法同样可以给出精度较高的结果。相比于Lévy解,本文方法可以处理非两端简支的边界条件;相比于有限单元法,本文方法计算成本较小,尤其对于高阶模态的求解,本文方法具有更显著的效率优势。另外,本文方法可扩展到任意边界条件下层合圆柱壳的强迫振动分析,相关工作正在开展中。 附录A 矩阵H中元素的表达式 由式(33)知矩阵H由3个子矩阵HA、HB和HC组成,下面分别给出上述3个矩阵的非零元素,由于HB和HC均为对称矩阵,此处只给出两者的下三角部分。 首先给出矩阵HA (A.1) (A.2) (A.3) (A.4) HA,34=-1 (A.5) (A.6) (A.7) 其次给出矩阵HB (A.8) (A.9) (A.10) (A.11) 最后给出矩阵HC (A.12) (A.13) (A.14) (A.15) (A.16) (A.17) 其中, (A.18) α2=A12D11-B11B12 (A.19) α3=B11D12-B12D11 (A.20) α4=A11B12-A12B11 (A.21) α5=A11D12-B11B12 (A.22) α6=A66R2+2B66R+D66 (A.23) α7=A66R+B66 (A.24) α8=B66R+D66 (A.25) (A.26) (A.27) (A.28) (A.29) (A.30) α14=A12B12-A22B11 (A.31) α15=B12D12-B22D11 (A.32) (A.33) (A.34) α18=B12D12-B11D22 (A.35)1.2 应力-应变关系
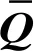
1.3 运动方程
2 辛体系下复合材料层合圆柱壳的控制方程
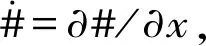
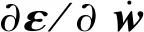
3 复合材料层合圆柱壳的自由振动分析
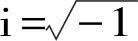
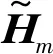
4 数值算例
4.1 两端简支边界条件
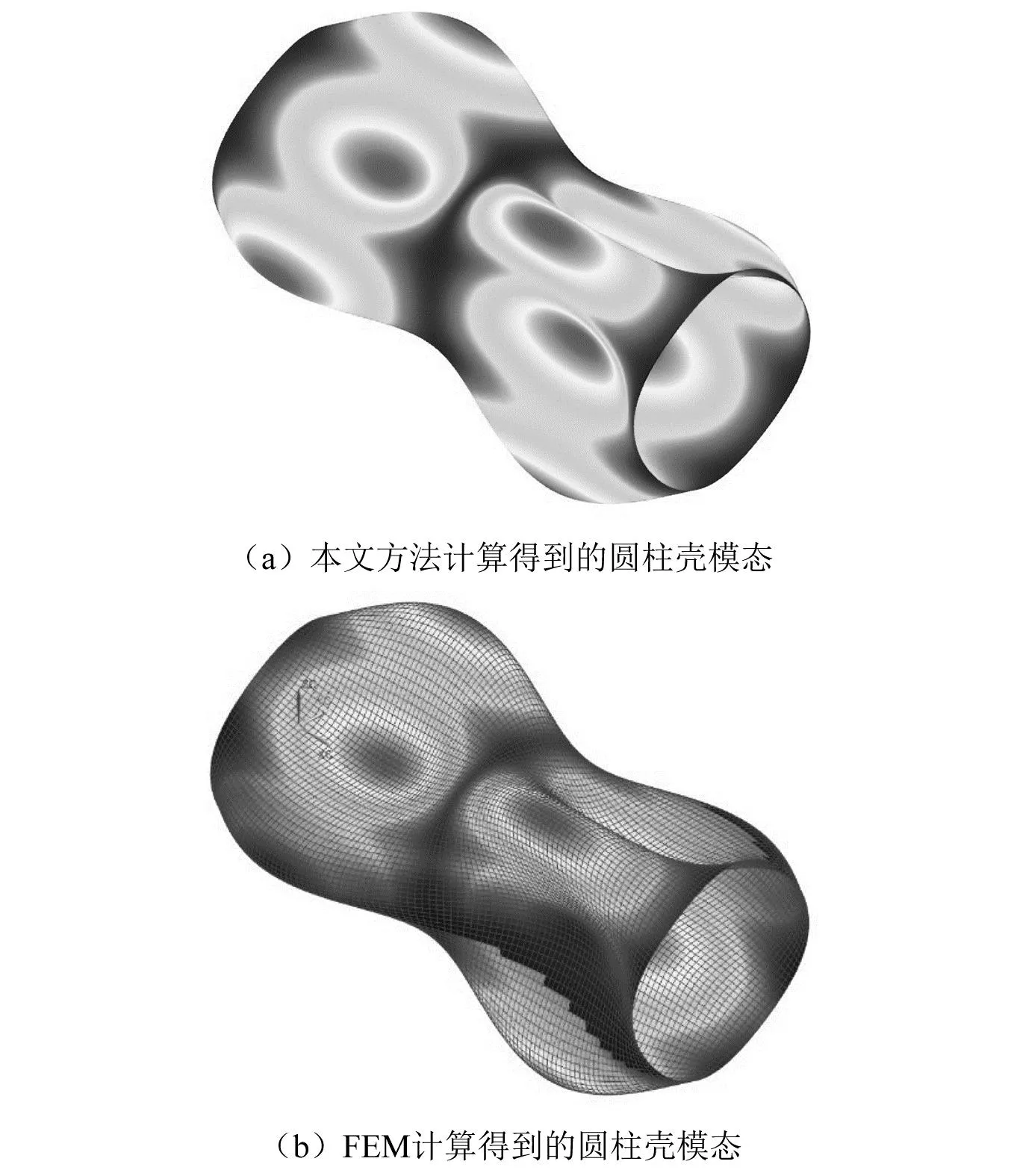
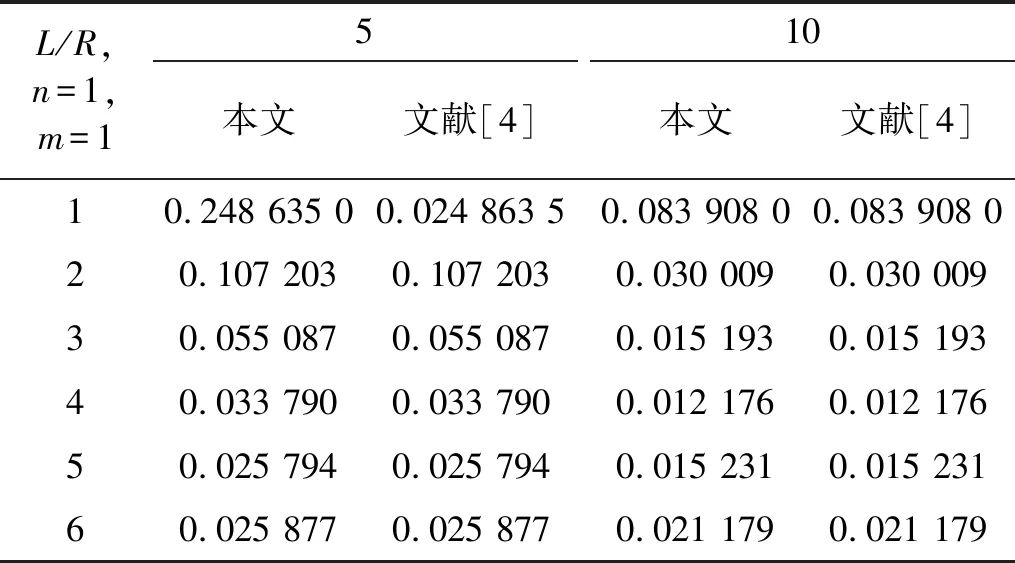
4.2 其他边界条件
5 结 论

