层合单元形函数的修正算法

彭文明，段云岭

(1.中国电建集团成都勘测设计研究院有限公司勘测设计分公司，成都，610072；2.清华大学水利系，北京，100084；3.水电水利规划设计总院，北京，100120)

1 前言

针对RCCD仿真模拟的问题，朱伯芳[1-2]首次提出了仿真分析的并层算法，把混凝土材料属性接近的浇筑层合并后统一划分网格，变成均质单元，以节省单元数和节点数，降低有限元分析中线性代数方程的个数。此后，王建江等[3]提出了“非均匀单元方法”；凌道盛等[4]构造出“虚拟层合单元”；朱岳明等[5]提出“非均质层合单元法”。这些方法在一定程度上解决了规模太大的问题，但是在计算过程中，单元均质化会带来误差。

非均质层合单元(以下统一简称“层合单元”)与常规均质单元采用一样的插值函数。当单元内各层材料属性相差较大的时候，这些插值函数描述的位移场与事实不尽相符。图1(a)为一个具有3层材料的层合单元，在均布荷载的作用下，变形如(b)中实线所示。这种变形后的位移场，用常规4节点等参元的双线性插值函数已经无法正确描述，如不做修正，将影响计算精度。

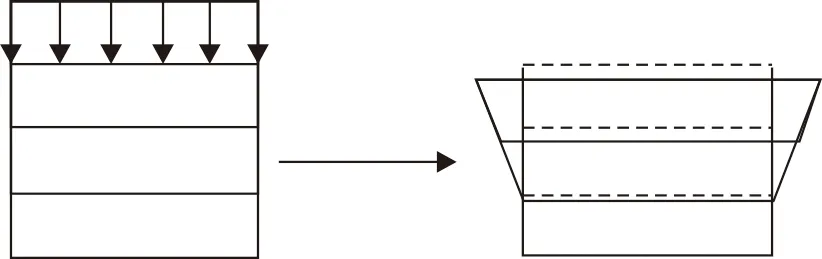
(a)初始单元 (b)变形后的单元

针对层合单元中不同层的位移场特点，本文尝试对常规层合单元(standard laminated element，简称为SLE)的位移插值函数进行适当修正，以便提高计算精度。修正后的层合单元记为“修正层合单元”(modified laminated element，简称MLE)，以示区别。

2 层合单元及其形函数

对于如图2所示层合单元，单元内含有n层材料，层厚分别为ti，材料均为各向同性。

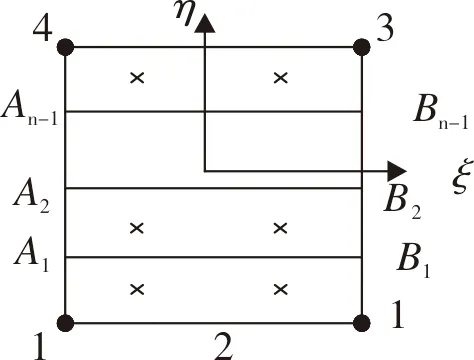
图2 层合单元

层合单元的形函数与常规四节点等参元一致，如下表示：

(1)

式中：Ni(i=1，2，3，4)为形函数；ξ和η为局部坐标系。

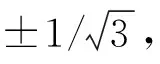
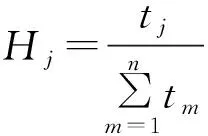
(2)

式中：tj为第j层材料的厚度；ηi-1和ηi分别为第i层材料界面的局部坐标值；n为材料层数。

所以分层积分方法共取2×n个积分点，权系数为：

Hij=HiHj(i=1,2；j=1,2,…n)

(3)

3 层合单元的形函数修正方法

层合单元的位移沿层厚方向不是线性变化，在层间的交界面上存在转折点。当各层材料属性相差较大时，单元内的位移场不适合用式(1)描述。在下面的修正中，我们将强制位移场满足层间交界面上的位移，体现各层材料对位移场的影响。

3.1 求解各层材料分界点的形函数值

为方便，假定泊松比都一样，设为ν。对于第i种材料，其弹性模量为aiE0(E0为常量)。假定单元内的平均应力为σ，每一层内应变为εi。对于平面应变问题有：

(4)

其中σz=ν(σx+σy)。

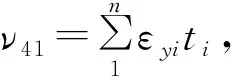
(5)

νAi可表示为：

νAi=αiν1+βiν4

(6)

其中αi+βi=1，而ν4=ν41+ν1，所以式(6)可写成

νAi=βiν41+ν1

(7)

(8)

由式(8)可求出N1在Ai的取值分别为αi(i=1，2，…，n-1)，N4在Ai的取值分别为βi(i=1，2，…，n-1)；如果各层材料在单元内厚度处处相等，可得N2在βi的取值为αi(i=1，2，…，n-1)，N3在βi的取值则为βi(i=1，2，…，n-1)。

3.2 采用高阶曲线修正插值函数

上节求解得到各层材料界面点的位移，可知层合单元位移曲线应为折线形。显然，用常规四节点等参元的双线性函数是无法准确多点折线的位移模式，本文采用高阶曲线修正插值函数。

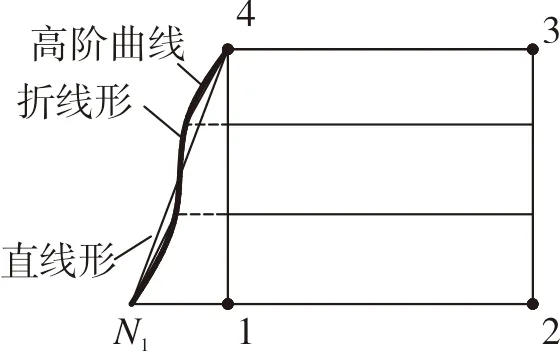
图3 层合单元变形示意

设插值函数为

(9)

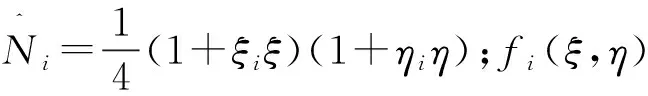
对于Ni来说，fi(ξ，η)应满足：①在边12、23、34上取值均为0；②在点Ai的取值使得Ni等于ai(i=1，2，…n-1)。

由条件①，可令

f1(ξ，η)=(1-ξ)(1-η2)g(ξ，η)

(10)

由于条件②中ξ为常量，则g(ξ，η)=g(η)，设为g(η)为η的多项式，如下：

(11)

其中sj为多项式系数。所以式(10)为：

(12)

由于N1在Ai中的取值已知，共有n-1个等式，最多能求解n-1个未知数，所以取m=n-2。设点Ai局部坐标为(-1，ηAi)，由式(8)-式(12)可得

(13)

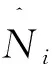
[β]{S}={C}

(14)

其中：

{S}=[s0s1s2…sn-2]T

{C}=[c1c2c3…cn-1]T

由于ηAi均不相等，B的行向量线性无关，于是|B|≠0，则有：

{S}=[B]-1{C}

(15)

由式(15)求出式(12)中的未知数{S}，f1(ξ，η)可以唯一确定。同理可求fi(ξ，η)(i=2，3，4)。fi(ξ，η)(i=1，2，3，4)有如下关系：

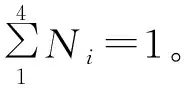
3.3 层合单元的积分格式

对于常规4节点等参元而言，其单元刚度矩阵[K]按式(16)求解：

(16)

其中：B为应变矩阵；D为弹性矩阵；J为雅克比矩阵行列式；h为单元厚度。

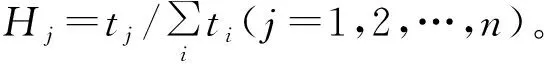
(17)

4 悬臂梁例题

图4为一个悬臂梁模型，尺寸为15m宽、4.5m高、1m厚，为平面应变问题。悬臂梁左侧固支，在模型右侧上方加一竖向集中荷载100kN，不计自重。用C语言编制层合单元有限元计算程序，分别采用常规层合单元和修正层合单元计算。模型网格划分为30个单元，44个节点。

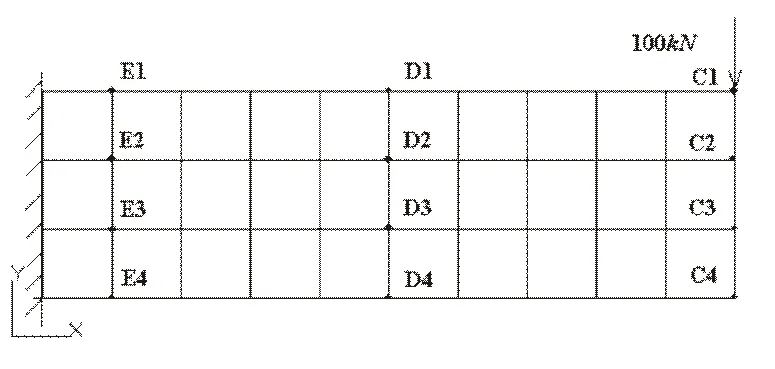
图4 悬臂梁模型

为检验修正层合单元函数的有效性，下面分两种情况计算：(1)每个单元内沿Y向包含5层材料(厚度均等)，由下而上材料的弹性模量分别为50GPa、45GPa、40GPa、35GPa和30GPa；(2)每个单元内沿Y向包含10层材料(厚度均等)，由下至上各层材料弹性模量等差递减：50GPa、47GPa、……、23GPa。材料的泊松比都取0.16。

为比较，还使用MSC.PATRAN &NASTRAN大型有限元商业软件对上述例子建模计算，商业软件没有层合单元计算模块，只能根据材料特性分别划分网格，5层材料时150个单元，176个节点；10层材料时600个单元，651个节点。单元网格分别是层合单元的5倍、10倍。

4.1 位移计算结果

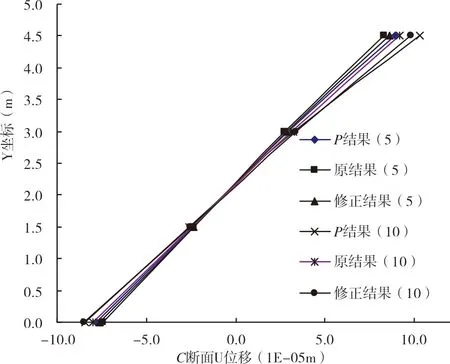
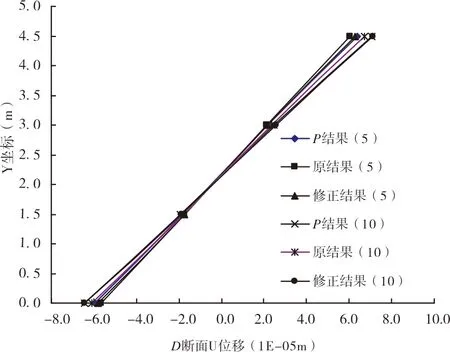
图5-图6是用上述三种方法计算得到C截面和D截面位移结果。图中的P结果(5)、原结果(5)和修正结果(5)分别表示PATRAN、常规层合单元和修正层合单元的计算结果，括号中的“5”表示5层材料。

(a)水平位移

(a)水平位移

从上述各图可以看出，由于层合单元内材料属性差异较大，如不修正插值函数，计算结果偏差比较大，严重影响计算精度；使用修正层合单元计算分析，精度得到明显提高。

4.2 应力计算结果

图7为D截面和E截面的X向应力计算结果。由于施加的外荷载不大，5层材料和10层材料在相同断面的σx应力值不大，其中在梁的上下面差值相对较大。

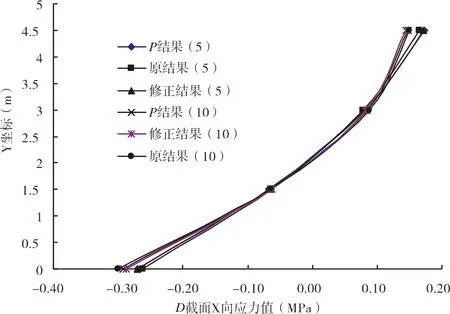
图7 D和E截面X向应力结果

4.3 计算成果对比

典型断面节点的位移和应力对比分析如表1所示。与商业软件对各材料划分网格的计算成果相比，常规层合单元的计算误差平均值在5%～6%，修正层合单元的计算误差平均值控制在1.5%～2.0%，计算精度有较大提高。

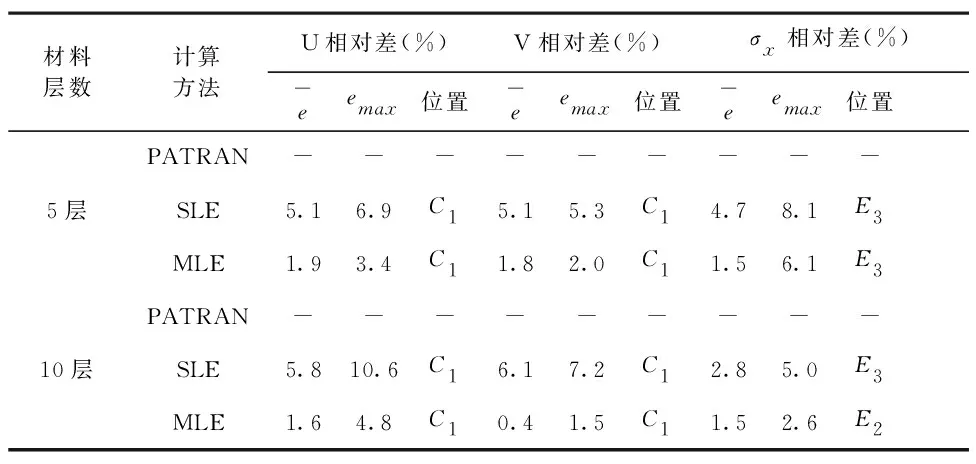
表1 计算结果对比

5 总结

层合单元对每层材料进行高斯积分，使得单元内材料属性可以不相同，为成层结构的仿真分析提供了一条切实可行的途径。由于各层材料属性不同，层合单元沿层厚方向的变形呈折线状，而它的形函数为双线性插值函数，该函数只能描述单向线性变化的位移场，所以在有限元分析时，层合单元只是用线性变化的位移场去逼近实际位移场。当材料属性相差较大时，上述逼近将产生很大误差。

本文在常规层合单元的基础上，根据其变形的特点，对层合单元的插值函数进行适当修正，修正后的插值函数可以表示为连续函数，充分考虑了单元内各层材料属性的差异，所以描述的位移场更能反映实际。算例表明，修正层合单元在不增加单元和节点的情况下，有效地提高了计算结果的精度，具有一定的工程应用价值。